基于蒙特卡洛算法的航空兵场站装备广义维修过程研究

刘 浏, 黄之杰, 刘慎洋

(空军勤务学院 航空四站系，江苏 徐州 230009)

0 引言

目前航空兵场站装备是我空军保障系统内技术含量较高，单装价值较高的保障装备之一，其维修性能的优劣直接影响航空兵场站的保障效能，进而影响航空兵的作战效能。而目前国内学者尚未给出一个适用于航空兵场站处于多级备件，(s-1,s)库存下的可修装备的维修性解析方法。陆中[1]等以Petri网模拟得出了逻辑维修关系下的维修性参数，却没有考虑库存备件在维修过程中的影响。罗祎[2]等给出了基于多级库存优化模型的维修性参数均值。陈童[3]等假设两级(s-1，s)备件情况下基层故障到达具有马尔可夫性，而真实情况下库存中，安装中的备件出现故障的可能性很小。本文针对航空兵场站装备中常见的多级备件(s-1,s)库存下的维修过程进行Monte Carlo(后简记为MC)仿真，得到的广义维修时间数据收敛于一稳态分布，再基于OLS估计和ML估计得到了该分布函数，并通过了卡方检验、Anderson-Darling检验、Kolmogorov-Smirnov检验。对比simlox软件评估结果，该MC仿真-OLS估计结果具有较高可信度。另外本文中所提供的算法可以较为自由的改变变量所服从的分布，对其他情况下的研究也具有一定借鉴意义。

1 装备单元维修模型MC仿真算法

1.1 基本假设

(1)航空兵场站装备单元寿命ξ服从指数分布Fξ(x)，且有密度函数fξ(x)=λie-λix,x>0,λ>0，装备由N个同型单元串联而成，装备故障率λ=Nλi且故障到达过程仅出现于备件在基层装备上正常运转时。

(2)修理人员仅在基层备件数大于0时，可对装备进行修理；若基层无备件则需等待备件到达。修理时间γ服从均匀分布Fγ(x)，备件更换后报废，装备修理如新，且有密度函数:

(1)

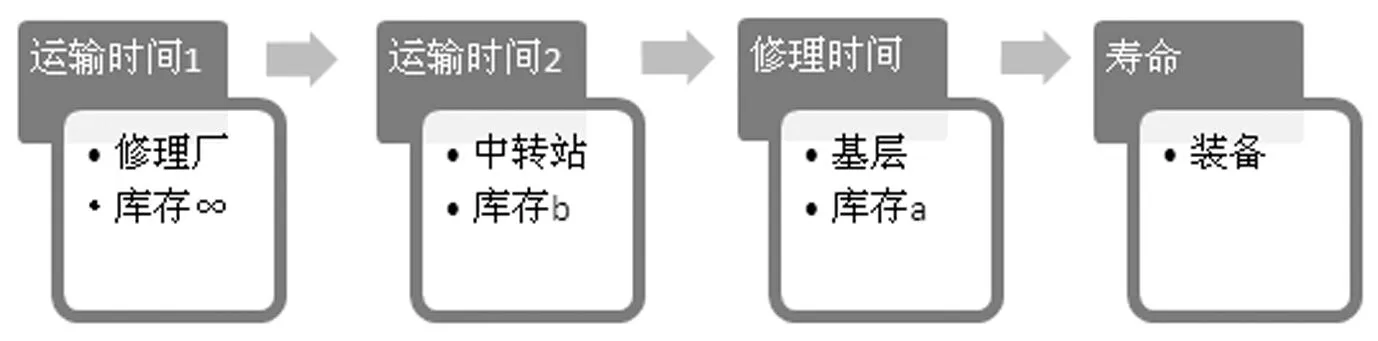
图1 维修所需备件的排队过程

1.2 维修过程的迭代表示

定义1映射A:Xn→R,A(A)=max{Ai,i=n-(a+2)}射,(Ai为随机向量正序第i个元素)易知A为定义在随机向量线性空间Xn上的一广义随机向量函数，R为实数空间。

定义2变量m1m2m3…m=1,2,3…n-2。

根据假设，构建迭代随机过程，如图2所示。

图2 维修时间与使用寿命交替的随机过程

其中ξn为寿命随机变量(后记为r.v.)，tn表示第n次故障的故障时刻。{tn,n>0}表示故障时刻为一连续时间序列过程，存在关系t1≤t2≤t3≤…tn，且满足迭代关系:

tn=tn-1+τn+ξn

(2)

易知维修时间γ与备件短缺时滞φ之和，即为广义维修时间τ=γ+φ。

定义4设τ(n)为参数n∈N*，定义于概率空间(Ω,F,P)上的一族取值于(R,R)的r.v.τ={τn,n∈N*}，且有如下迭代表示:

(3)

δ=A(a)ε=A(b)

当且仅当事件ω∈Ω，且c,g中r.v.满足

x1(ω)≥x2(ω)≥x3(ω)≥…≥xn-2(ω)y1(ω)≥y2(ω)≥y3(ω)≥…≥y2n-b-3(ω)

a=[x1x2x3…xn-2]T,b=[y1y2y3…y2n-b-3]T时，有:

c=[τn+ξnτn+ξn+τn-1+ξn-1

τn+ξn+τn-1+ξn-1+τn-2+ξn-2…

(4)

g=[f,d]T

(5)

d=[τn+ξnτn+ξn+τn-1+ξn-1

τn+ξn+τn-1+ξn-1+τn-2+ξn-2

(6)

其中，f′=f-[αm1αm2…αmn-b]T。

当且仅当事件ω∈Ω，且r.v.取值为ζm(·)时，有如下关系：

ζm1(ω)≥ζm2(ω)≥ζm3(ω)…≥ζmn-b(ω)

记随机向量f,e可分别表示为:

f=[ζm1ζm2…ζmn-b]T

(7)

e=[τn-1+ξn-1τn-1+ξn-1+τn-2+ξn-2

τn-1+ξn-1+τn-2+ξn-2+τn-3+ξn-3

(8)

以映射C来表示e=[ζ1ζ2…ζn-2]T

1.3 算法流程，结果及收敛性

1.3.1 算法流程

仿真算法流程示意图，如图3所示。

图3 仿真算法流程简示(虚线:数据读取,实线:逻辑顺序)

1.3.2 随机数检验

算法流程中所使用随机数来自线性同余-反变换发生器，因为反变换法以均匀随机数为基础进行变换，现仅对其均匀随机数输入进行检验。据表1检验结果，可以认为该数列满足随机性要求，算法可信度较高。

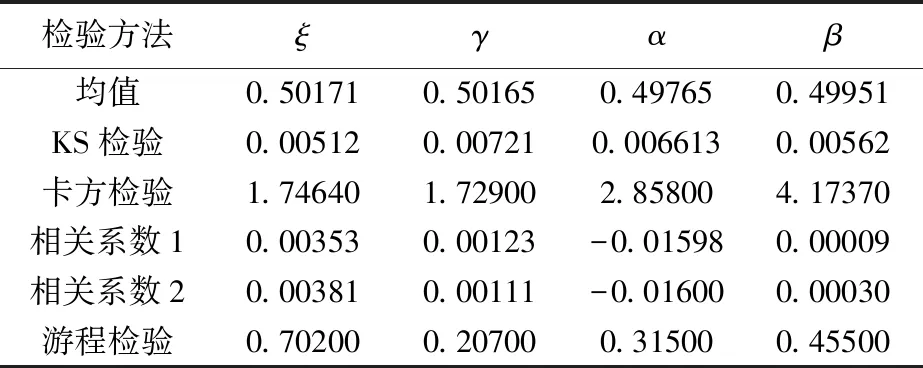
表1 对四种随机数输入值的检验

表2 对三类分布的拟合检验

1.3.3 仿真结果

现根据某场站低可靠性可修装备(λ取值较大)及其可靠性，库存量等数据对其维修过程进行仿真,迭代次数n∈[1,2.5×104]。其τ(n)如图4:

图4 仿真周期内样本曲线

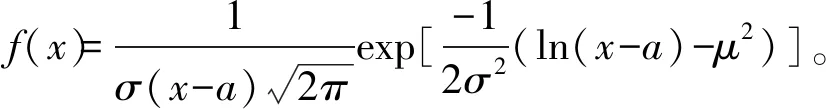
由图5(b)(c)(d)可见：当n∈[2.0,2.1](×104)时异常值较为明显(深色标出)；当n∈[2.1,2.2](×104)时数据频率分布异常值明显减少；可以得到随着n的不断增大，样本频率分布逐渐平滑收敛为一对数正态密度函数；由图5(b)(e)(f)可见，当n∈{[2.0,2.1],[2.0,2.3],[2.0,2.5]}(×104)，随着样本容量的扩大，τ具有明显频率稳定性。

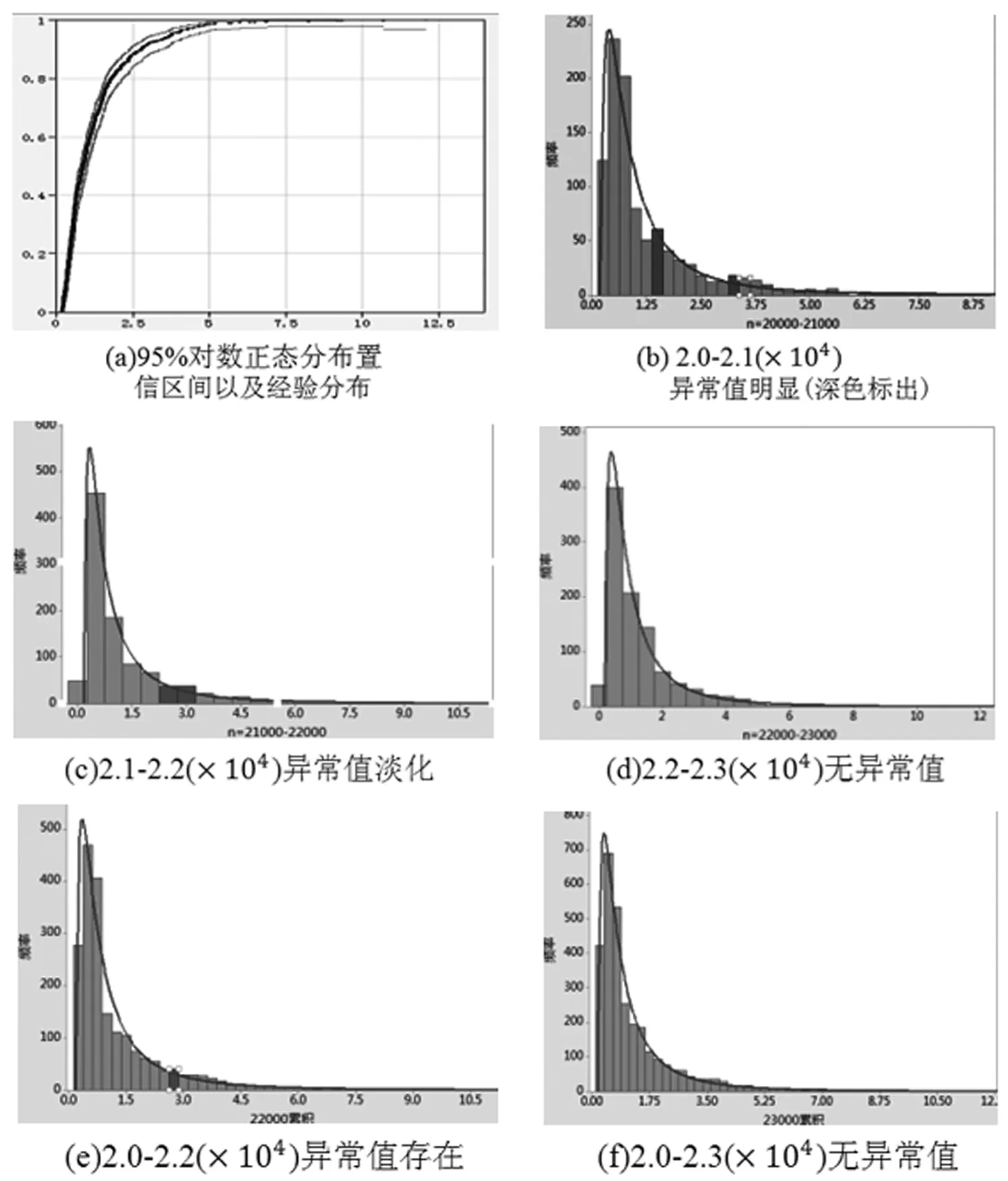
图5 n→∞以及扩大样本的分布拟合效果

分别对n∈{[2.0,2.1],[2.1,2.2],[2.2,2.3]}(×104)的数据进行对数正态性拟合检验，结果如表3所示。

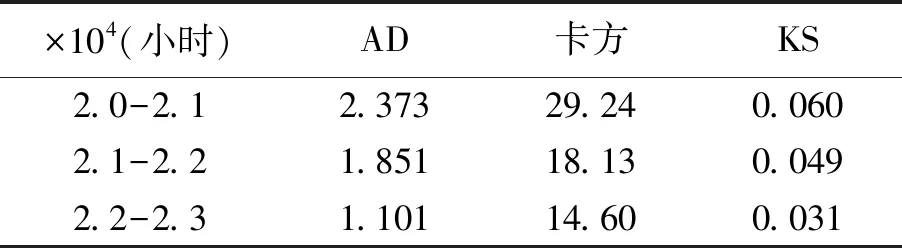
表3 n→∞时分布拟合程度不断优化

综上所述，随着n→∞,τ(n)的一维分布序列

(9)

1.3.4 收敛性分析

易知迭代随机过程τ(n)，n=0,1,2,3…为一可数无穷维随机过程[4](定义4)。因此满足性质:(1)相容性条件;(2)对称性条件。

其r.v.依分布收敛等价于每一个有限维分布的弱收敛[4]。

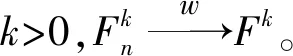
由性质可知，τ(n)的有限维分布族：

F(n1,n2,…,nw;x1,x2,…,xw)

=F(n1,nw,nw+1,…,nu;x1,x2,…,xw,∞…∞)

(10)

根据式(9)，命题得证。

2 广义维修时间分布的参数推断

样本{τ1,τ2,τ3,τ4…τm,τm+1,τm+2…τm+n}来自随机过程τn。当m→∞，{τm+1,τm+2…τm+n}可认为是一来自一维稳态分布F(1)的样本，且τm+1τm+2τm+3…τm+n|m→∞,其观测值的次序统计数据为{x1,x2…xn},其密度函数为f(x,Θ)。

2.1 推断结果

现基于Minitab对n∈[2.2,2.3](×104)时的样本分别进行最小二乘估计(OLS)，极大似然估计(ML),估计结果及95%置信区间如表4所示。

表4 估计结果

由于两种方法的拟合结果相近，所以其图像不再单独列出。

2.2 拟合检验

对比OLS，ML估计方法所得估计量的拟合程度，结果如表5所示。

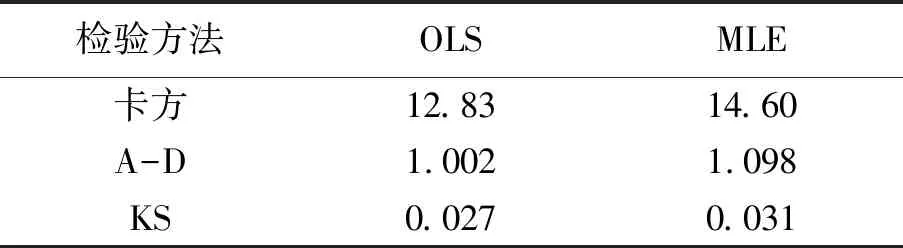
表5 拟合检验

可以得到：OLS方法得到估计结果拟合程度优于ML。可以认为该型装备维修时间τ在达到稳态后，τ～LN(0.13,-0.31,0.98)，且有密度函数：

(11)

3 结论

根据维修性定义及(11)式得

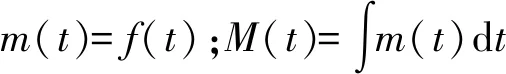
(12;13)

m(t)—维修密度函数；M(t)—维修度函数,即：

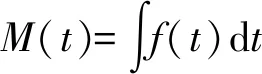
(14)

MTBM—维修间隔时间；MTTM—维修时间。

代入的仿真数据可得A0≈19%，相比国外成熟软件平台simlox对该型装备效能仿真结果(A0)如图6所示，拟合度较为理想。

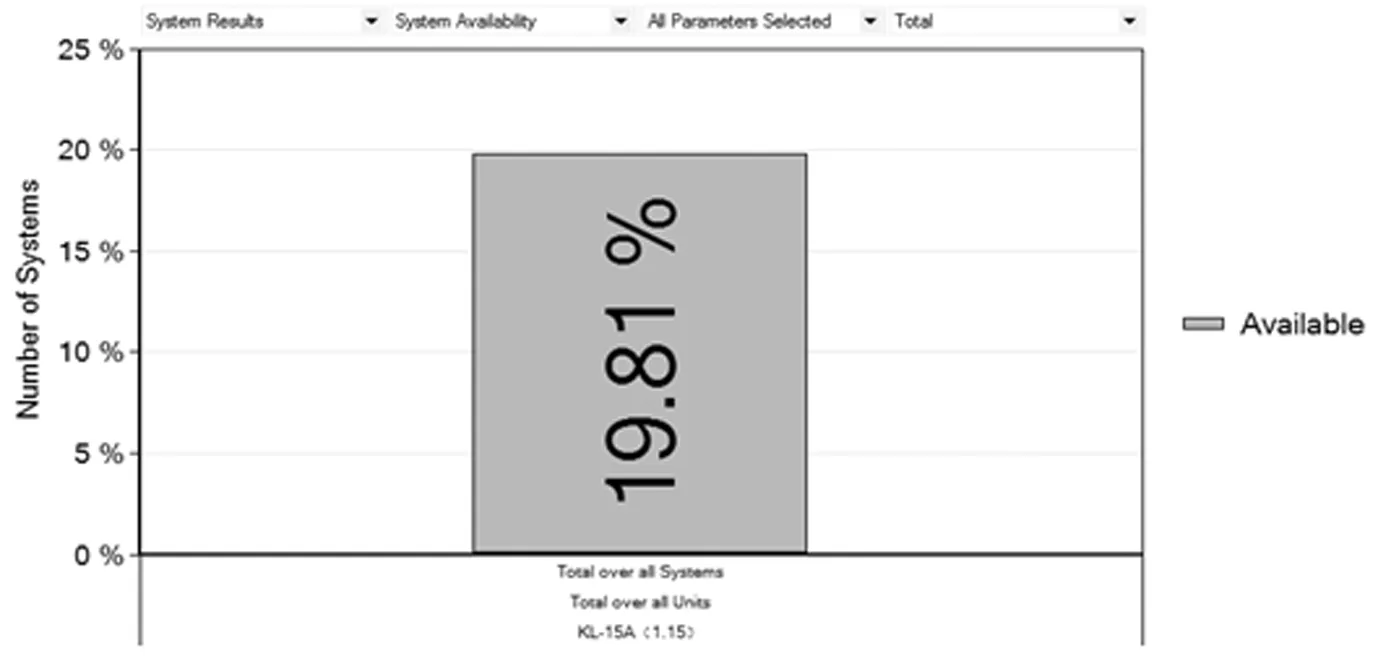
图6 simlox软件平台稳态可用度仿真结果

因此可得：

(1)在误差允许范围内，在假设情况下该装备的稳态可用度，稳态维修度函数分别为A0，M(t)。

(2)在假设条件下，本MC仿真-OLS估计方法可作为多级备件条件，(s-1,s)库存下的装备可用度，维修度解析模型。