APM车辆导向力矩优化分析

唐 飞，李 耀，朱福成

(1. 重庆中车长客轨道车辆有限公司 技术部，重庆 401133； 2. 重庆交通大学 轨道交通研究院，重庆 400074； 3. 中铁三局集团桥隧工程有限公司，四川 成都 610036)

旅客自动输送系统(APM)，也称为自动导轨快捷运输系统(AGT)，是一种无人驾驶、立体交叉的公共运输系统[1]。APM交通因具有智能驾驶、安全舒适、运量灵活、运输效率高、成本低、曲线半径小等独特优势，在全国范围内得到快速发展。

APM车辆最大特点是最小曲线通过半径较其他城市轨道车辆小，平面最小曲线半径仅为22.8 m。为保证APM车辆在小曲线半径的曲线通过能力，对APM车辆导向性能进行优化分析是十分重要的环节[2]。车辆通过曲线时，其转向架与轨道之间相互作用产生的促进车辆转向力矩称之为导向力矩，导向力矩是衡量APM车辆导向性能优劣的重要指标[3]。故对APM车辆导向力矩进行分析及优化，对APM车辆动力学性能研究具有指导意义。

1 APM车辆模型建立

1.1 APM车辆系统

APM车辆主要由列车自动控制系统、走行部、车厢、牵引制动系统、通风照明系统等组成，其技术参数见表1。

1.2 转向架结构

APM车辆转向架主要由轮胎系统、驱动桥、悬架、空气弹簧、减震器、钢板弹簧、回转支撑、平衡杆、牵引电机组成[4]，其三维模型如图1。

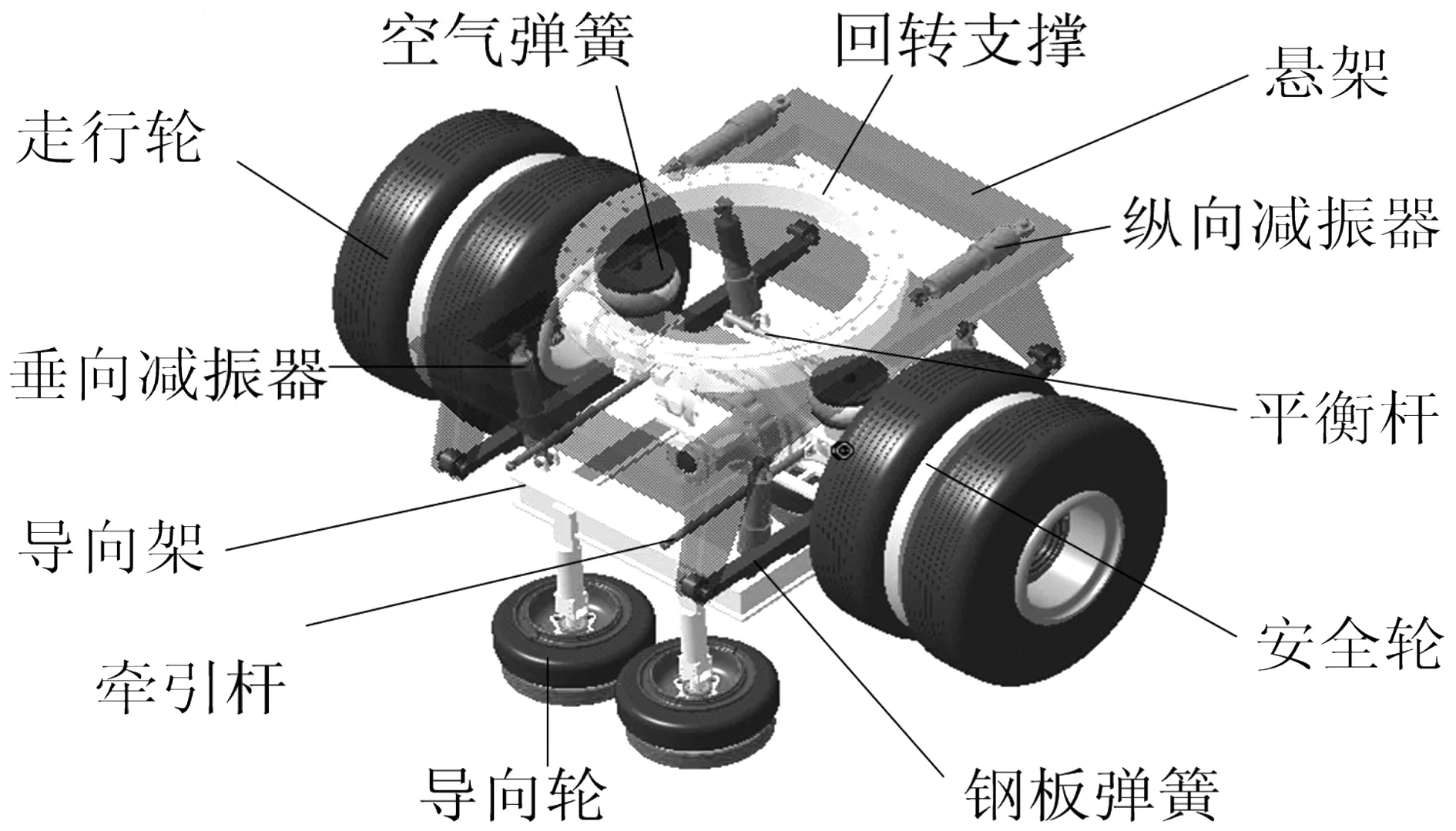
图1 APM车辆转向架三维模型Fig. 1 Three-dimensional model of APM vehicle bogie

2 APM车辆动力学模型建立

2.1 车辆拓扑构型

APM车辆系统作为一个多刚体耦合系统，在建立动力学模型之前应对其结构进行合理简化、等效，再根据结构和受力关系建立其拓扑构型[5]，如图2。

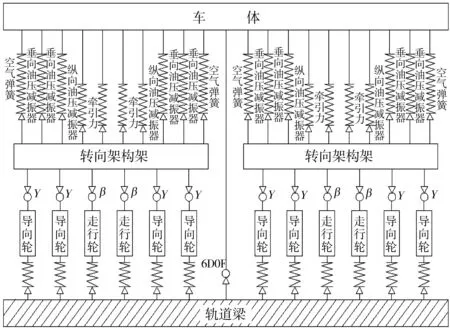
图2 APM车辆拓扑构型Fig. 2 Topology configuration of APM vehicle

2.2 动力学模型建立

按照APM车辆拓扑构型，笔者运用Adams建立APM车辆系统动力学仿真模型，轮胎采用UA模型，路面采用随机干扰路面[5-6]，如图3。

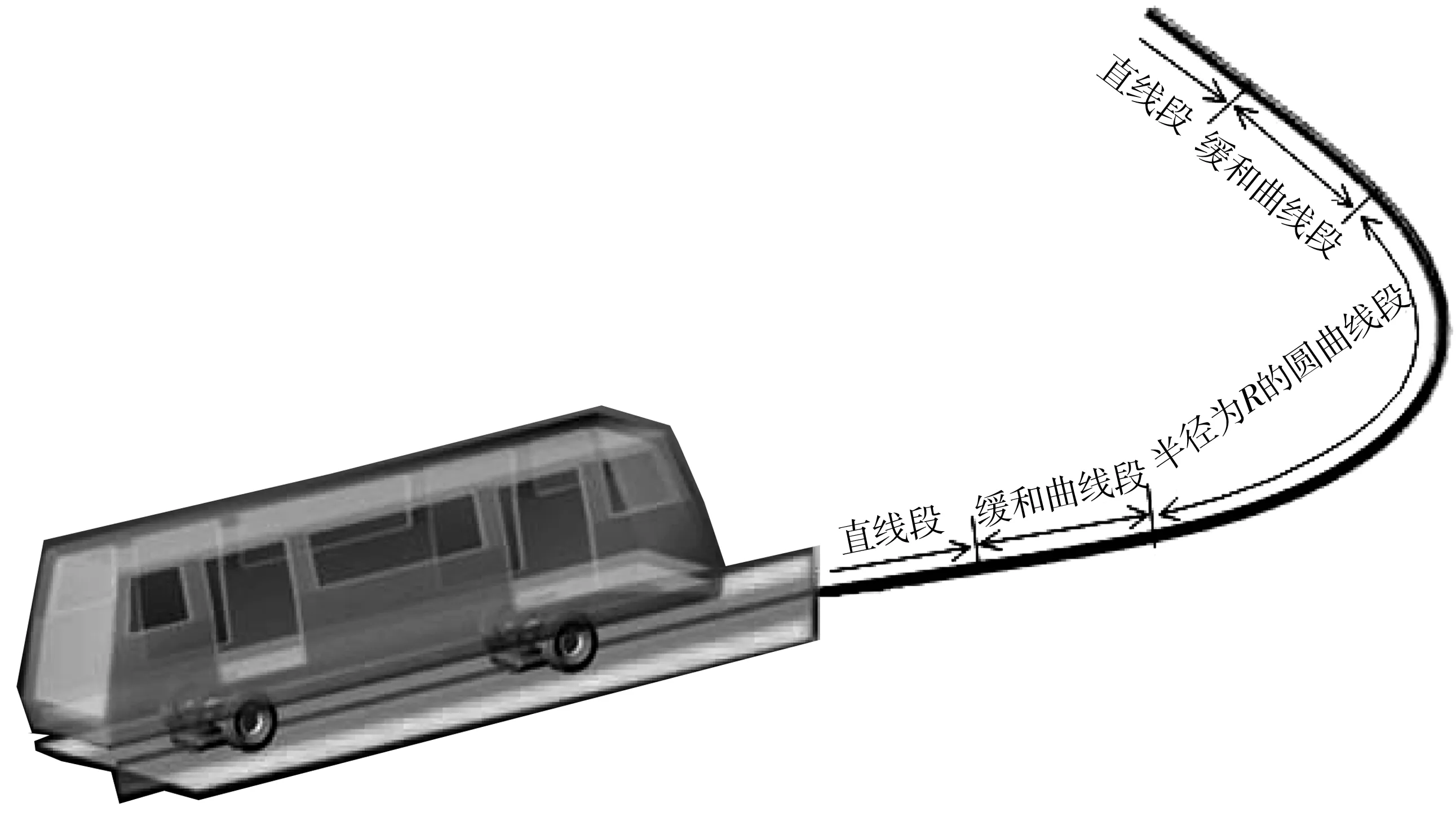
图3 APM车辆动力学模型Fig. 3 Dynamics model of APM vehicle

3 敏感性分析

APM车辆系统作为复杂的非线性系统，具有高度相互关联性，系统参数变化范围广，参数优化工作量大，耗时较长[7]。灵敏度分析可识别各参数对导向力矩的影响程度，从而选择主要影响因素进行优化，能缩小优化工作量、节省时间、提高效率。

3.1 影响因素

笔者选取轮胎、空气弹簧、减振器等力学特性参数作为APM车辆导向力矩影响因素，如表2。

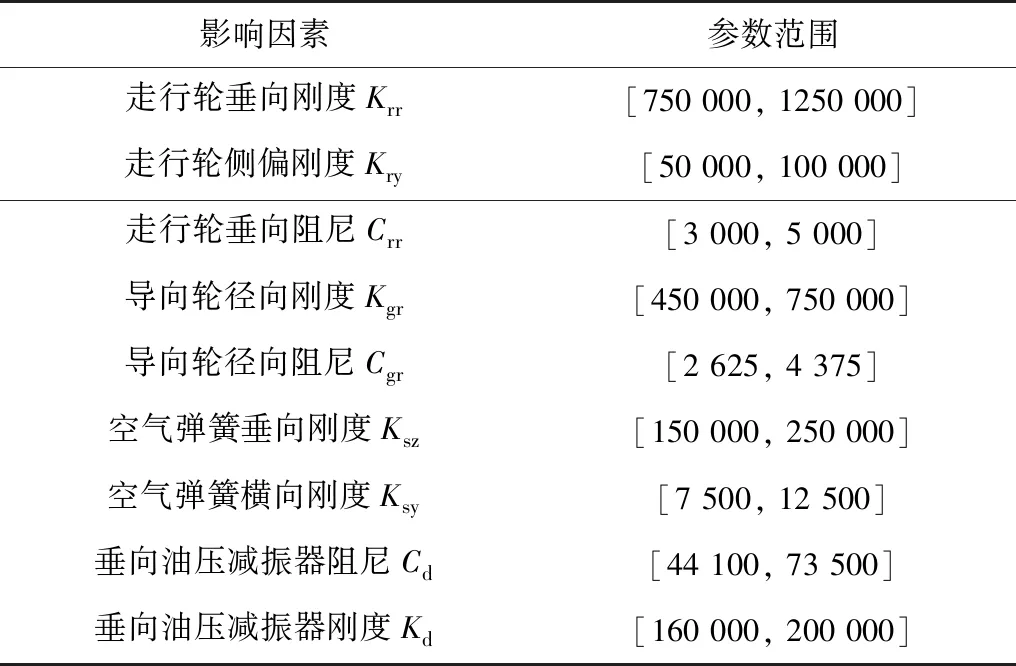
表2 影响因素参数Table 2 Influencing factor parameter N/m

3.2 目标函数

APM车辆通过曲线时，转向架与轨道相互作用，产生促使车辆按既定轨道运行的力矩(图4)，称为导向力矩[8]。

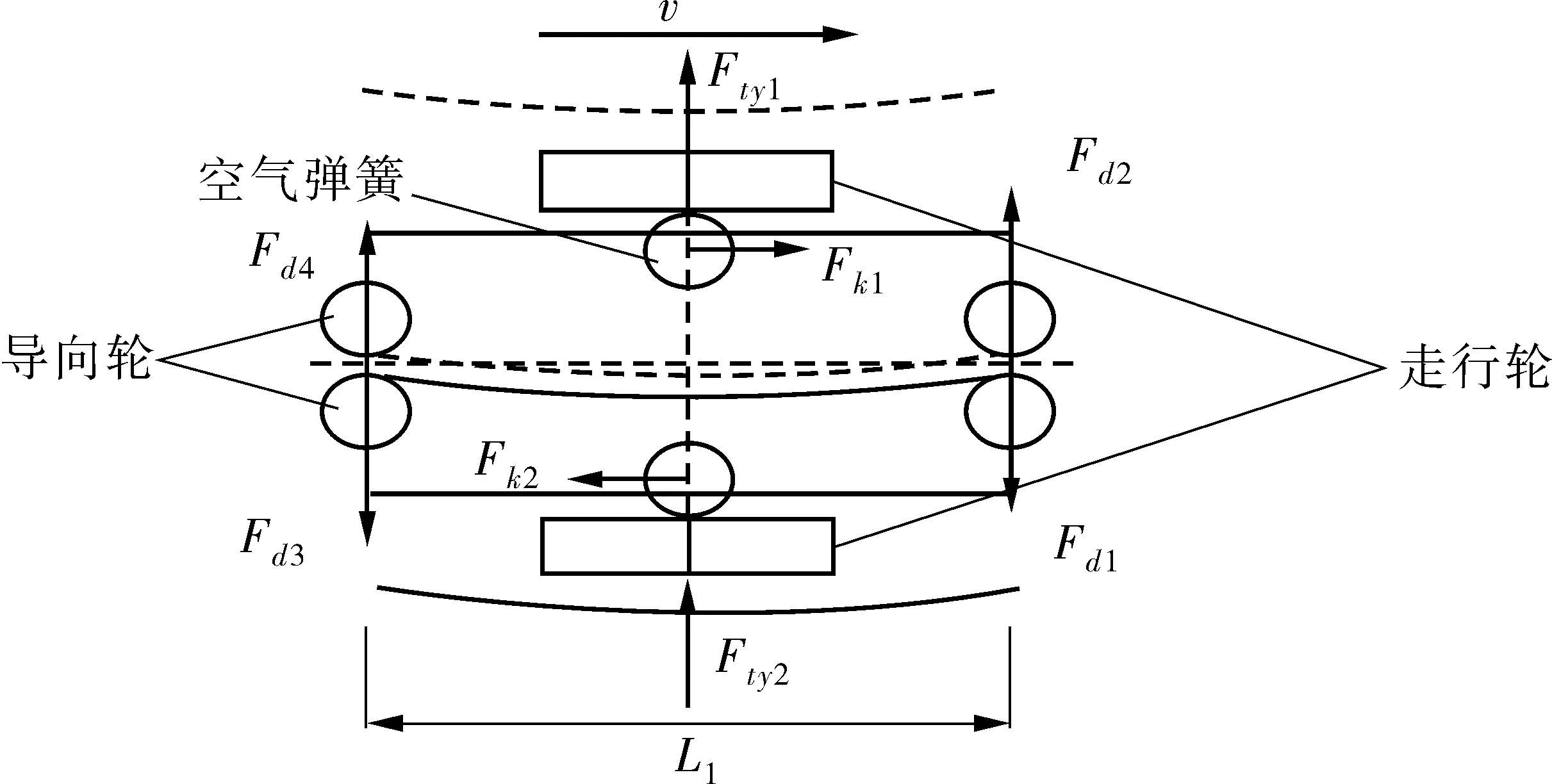
图4 转向架受力分析Fig. 4 Analysis of bogie force

其导向力矩的计算如式(1)：

Mg=(Fg2+Fg3-Fg1-Fg4)×(L1/2)

(1)

式中：Mg为导向力矩，N·m；L1为导向轮纵向间距，m；Fg1～Fg4分别为导向轮径向力，N。

3.3 灵敏度分析模型

笔者运用Adams与modeFRONTIER联合建立APM车辆导向力矩灵敏度分析模型，如图5。

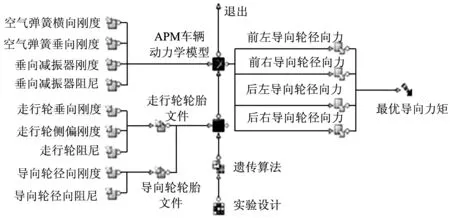
图5 灵敏度分析模型Fig. 5 Sensitivity analysis model

3.4 灵敏度分析

灵敏度大小结果见表3；导向力矩灵敏度分析如图6。

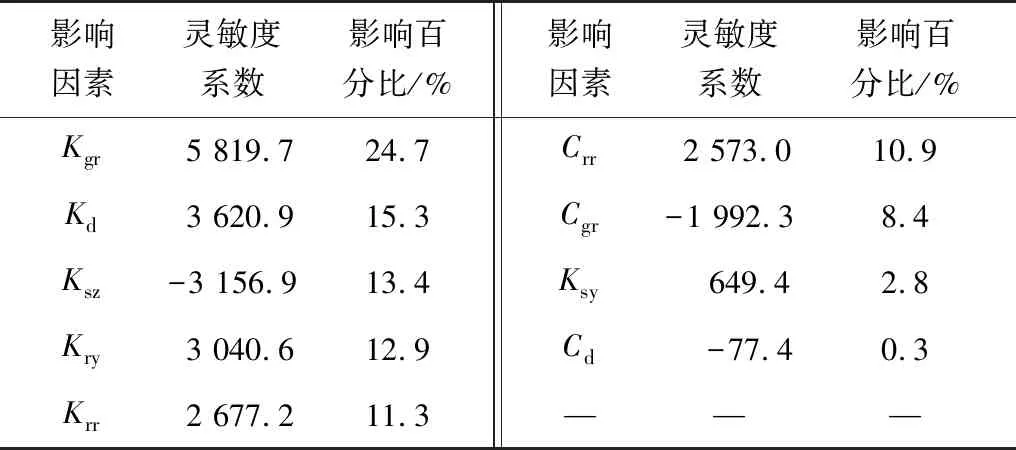
表3 灵敏度结果Table 3 Sensitivity results

从图6可看出：各影响因素对Mg灵敏度大小为：Kgr>Kd>Ksz>Kry>Krr>Crr>Cgr>Ksy>Cd。其中：Kgr、Kd、Ksz、Kry、Krr为影响Mg的主要因素。

4 APM车辆导向力矩优化

4.1 优化变量

笔者选取影响APM车辆导向力矩Mg的5个主要因素Kgr、Kd、Ksz、Kry、Krr作为优化变量。

4.2 约束条件

4.2.1 曲线通过性分析

1)轮重减载率

轮重减载率的计算如式(2)。

(2)

式中：ΔP为减载侧轮重减载量，N；P为减载侧与增载侧平均静轮重，N；P1为减载侧轮重，N；P2为增载侧轮重，N。

2)走行轮最大垂向力

为保证车辆稳定性和安全性，车辆通过弯道时走行轮最大载荷应小于轮胎额定负荷为70 kN。

3)导向轮最大径向力

导向轮组成包含橡胶轮胎和铝合金安全轮，当轮胎压缩量大于轮胎与安全轮半径之差时，安全轮与轨道接触，此时易加剧轮胎和轨道的磨损，影响车辆安全运行[9]。因此，导向轮径向力应小于最大径向力，如式(3)。

Fgmax=kgΔy=33 000 N

(3)

式中：Fgmax为最大径向力，N；kg为径向刚度，N/m；Δy为压缩量，mm。

4.2.2 运行平稳性、舒适性分析

1)车体振动加速度

车体振动加速度为：Ay=Az≤2.5 m/s2。

2)车体临界侧滚角

4.3 优化模型建立

笔者采用优化程序与动力学计算集成方式进行，优化过程由modeFRONTIER调用动力学模型完成，选择NSGA-II为优化算法[11]，如图7。

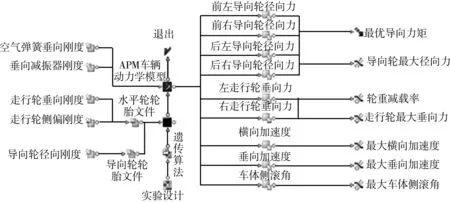
图7 导向力矩优化模型Fig. 7 Optimization model of steering torque

4.4 优化结果分析

在约束条件下，经过1 000次迭代后，导向力矩Mg收敛于一点，如图8。优化目标与设计变量之间的变化规律如图9。

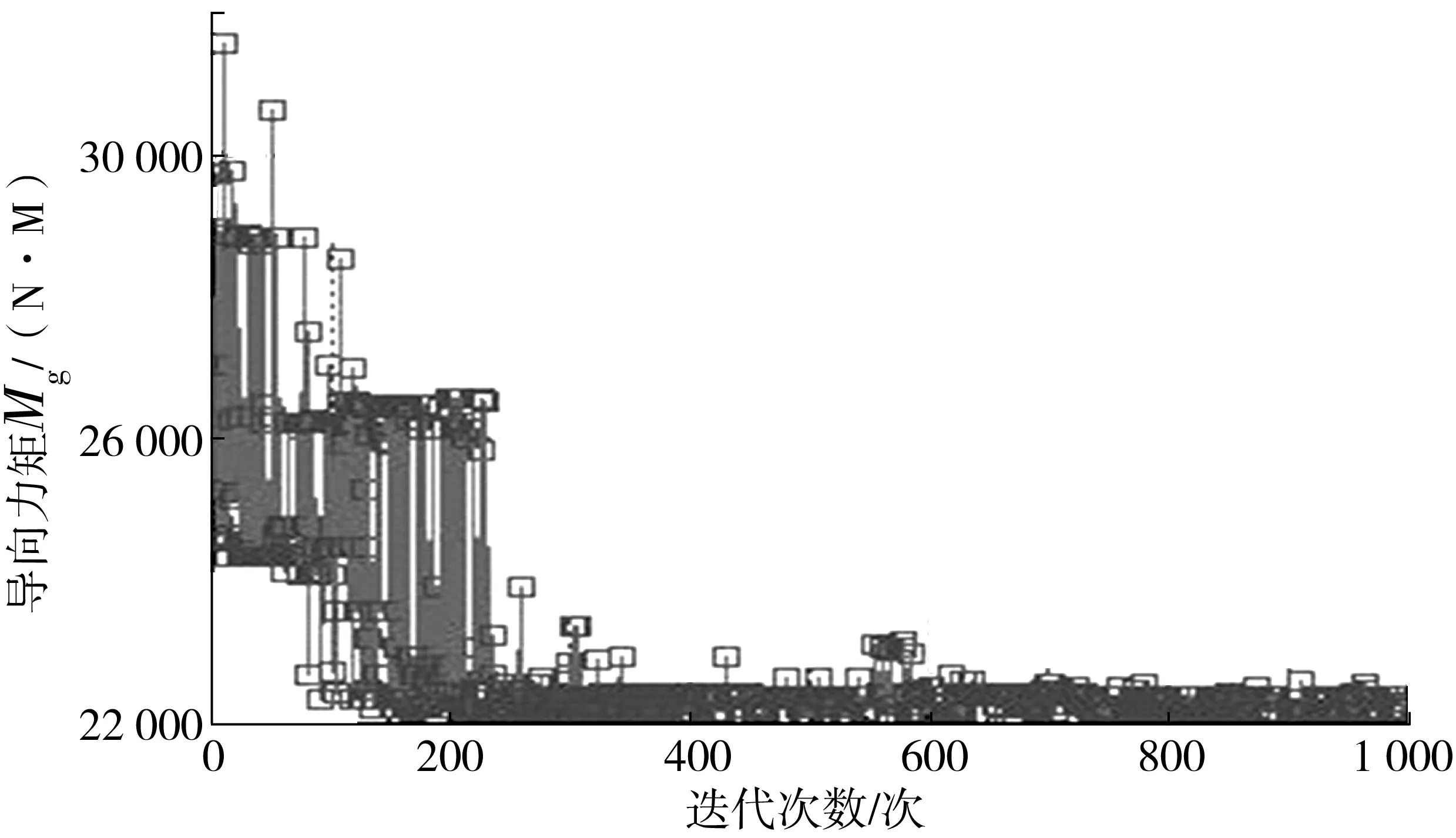
图8 导向力矩优化过程Fig. 8 Optimization process of steering torque

通过线性回归分析(图9)：Kgr、Kd、Kry、Krr与Mg均呈线性正相关，这表明适当减小Kgr、Kd、Kry、Krr有助于提高车辆的导向性能；Ksz与Mg呈线性负相关，说明适当增加Ksz有助于提高车辆导向性能。

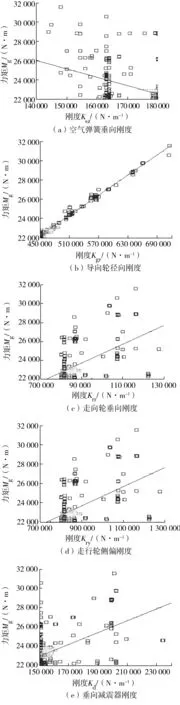
图9 设计变量与导向力矩关系Fig. 9 Relation between design variables and steering torque

当Ksz=180 000 N/m、Krr=813 800 N/m、Kgr=450 100 N/m、Kry=76 334 N/m、Kd=150 000 N/m时Mg达到的最优值。此时，Mg从26 241 N·m减小到22 142 N·m，减小了4 099 N·m，优化了15.6 %。不同曲线半径的优化结果，如表4。

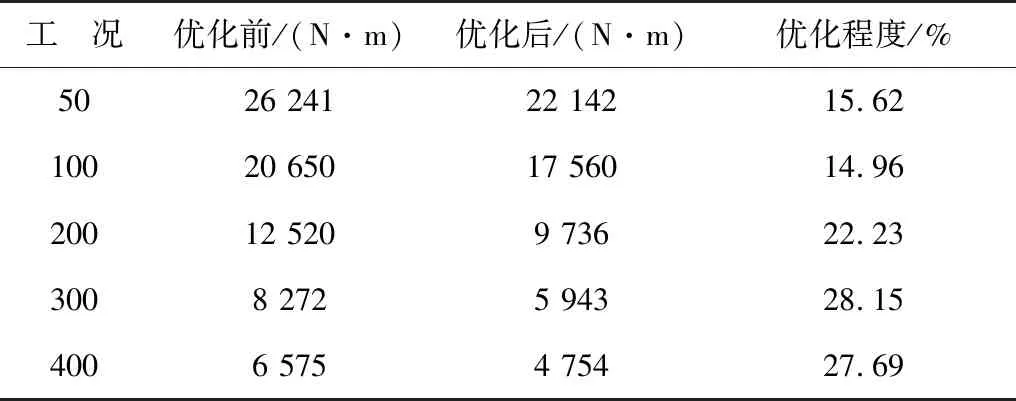
表4 导向力矩优化结果Table 4 Optimization results of steering torque

通过优化，不同曲线半径下导向力矩降低了26.57%～38.57%，APM车辆的导向性能得到了有效提高。

5 结 论

1)灵敏度分析发现Kgr、Kd、Ksz、Kry、Krr是影响APM车辆导向力矩Mg的重要参数；除Ksz与Mg呈线性负相关外，其余4个参数与导向力矩之间均呈线性正相关；

2)通过线性回归分析发现：Kgr、Kd、Kry、Krr与Mg均呈线性正相关；Ksz与Mg呈线性负相关；

3)当Mg达到最优时，此时在半径50、100、200、300、400 m这5种弯道下导向力矩Mg降低了14.96%～28.15%。这表明APM车辆导向性能得到了有效提高。