不同站台环境下公交车停靠时间的动态预测模型
邓 媚,李春达
(1. 华蓝设计(集团)有限公司,广西 南宁 530011; 2. 广西建设工程项目管理中心有限责任公司,广西 南宁 530022)
0 引 言
城市公交系统的运行效率受到道路交通状况、天气条件、公交车的停靠时间和换乘乘客人数等因素的影响。其中公交车在公交站台的停靠时间是公交车运行时间的一个重要因素,也是影响公交系统通行效率的主要来源。根据美国道路通行能力手册的定义,公交停靠时间是公交车为了等待乘客上下车而在公交站台停车等待的时间。从公交车打开车门等待乘客下车的时刻Topen开始,到公交车门关闭的时刻Tclose为止,DT是这两个时刻的时刻差,即DT=Topen-Tclose[1]。为了获得公交停靠时间与公交运营时间的量化关系,美国华盛顿特区公共交通局采集了其所辖区域内的公交停靠时间数据,并将该数据开放给乘客使用,帮助该地区的乘客获得公交车在不同站台的停靠时刻,提高华盛顿地区公交线路服务系统的可靠性。
由于城市公交线路服务的可靠性是城市公交系统服务优劣的重要评价指标[2],而公交停靠时间可以反映出不同站点,不同时段的客流量分布,且公交停靠时间分布是可量化的数据指标,因此很多研究通过分析公交停靠时间变化趋势来评价城市的公交服务质量。例如,苏荣霖等[3]对公交站台的客流量分布与公交停靠时间影响进行进一步的量化分析,构建了乘客上下车时间与公交停靠时间分布的映射模型;李凯胜等[4]分析了公交线路站点设置与公交停靠时间的关系。但这些研究并没有考虑时段和公交站类型对公交停靠时间分布的影响。通过人工方式采集公交停靠时间数据需要耗费大量的人力、物力和财力[5-6],因此领域内基于公交停靠时间的研究都是小样本容量的数据分析。
为了更好的预测公交车停靠时间,有研究人员结合不同地区的公交车乘客数,车费付费类型和公交车扣费时间等多项数据研发公交停靠站预测系统[7]。王旭[8]等对北京市23条公交线路的停靠站时间进行分析,结合每站乘客换乘人数,车门数,车上乘客数等因素对公交车停靠站时间进行建模预测。乘客上下车行为是影响公交车停靠站时间的关键因素之一[9],因此部分研究人员通过分析乘客上下车过程中的关键动作,建立乘客上下车时间与公交停靠时间的统计模型。吴洋[10]等对无人售票公交车的停靠站时间与乘客行为进行分析,发现车内乘客密度大于公交车的临界乘客密度时,公交停靠时间与公交系统的扣费时间及乘客下车速率成正比关系。车内乘客密度较小时,公交停靠时间与乘客付费后移动至车内站位(座位)的速率成正比[11]。上述模型并没有考虑到高峰和平峰时段对公交停靠时间的影响,也没有定量分析公交站类型与公交停靠时间的关系。实际上,公交站类型、车门类型和数量、车站拥挤度等因素对公交停靠时间分布具有极其重要的影响[12-13]。考虑到乘客出行主要包含早、中、晚3个高峰时段,乘客的出行服务时间在此3个时段可能不尽相同,因此对公交停靠时间的影响也略微不同。
以上的公交停靠时间统计模型虽然考虑了乘客数、车费支付方式、公交车门类型和数量等常见因素,但没有过多的考虑公交站台位置(交叉口站点和干道站点)和不同时段(早高峰、午高峰和晚高峰时段)对公交停靠时间分布的影响,且没有根据我国城市数据对模型参数进行标定。本研究对广西南宁市的公交停靠数据进行调查分析,获得不同时段下不同公交站台环境下的公交停靠时间数据分布,量化评价公交站台环境和时段对公交停靠时间的影响。研究结果可以用于估计不同时段下公交线路在不同站点的停留时间和到站时间,提升城市公交线路的服务质量和乘客感知。该研究成果也可帮助公交公司在节假日等特殊事件下设计出合理的公交运营时刻表。
1 数据与方法
1.1 数据来源
广西南宁市作为北部湾城市群的区域性国际都市,具有丰富的旅游资源。近年来日益增加的居民、游客和通勤人员导致当地公交需求呈现出明显的潮汐特性。早高峰时期,乘客客流从城市郊区方向涌向市区CBD区域;晚高峰期间,客流从城市中心区域回流至市郊。虽然特区共有多个公交站点,只有部分公交站点在分析客流潮汐现象和公交停靠时间分布比较重要。因此,本研究将青秀区、兴宁区内公交站点的日乘客人员总数进行排序,选择客流量较大的和干道站点(共13座公交站点)作为我们的研究对象,其中邻近交叉口的公交站点7座,干道公交站点6座。
通过人工方式采集上述公交站点高峰时段(早上7—9点,中午12—2点,下午4—6点)的公交停车时间、乘客等待时间等数据。除了上述公交停靠相关数据,我们也采集了公交站台的相关参数,比如公交站台的车道数,公交站台的长度,站台附近是否有可用停车位等。采集的这些数据与公交车停靠时间计算有着直接的关系。在公交站点共采集到261车次的公交车停靠站事件,总共有250个有效的公交车公交停靠时间序列。
1.2 公交停靠时间统计模型
我们通过采集公交车在公交站点外等待进站时间、公交加速进入公交站台时间、公交车在公交站台实际停靠时间和公交车加速驶离站台时间,公交车上下车乘客人数及公交车的车门关闭时间。对不同站台环境下的早、中、晚三个高峰时段构建式(1)所示的广义公交停靠时间回归模型:
DT=k1·T1+k2·T2+k3·T3+k4·T4
(1)
式中:DT为广义公交停靠时间;T1为公交车在公交站点场外的等待时间;T2为公交车加速进入公交站点的时间;T3为公交车公交站点的实际停靠时间;T4为公交车加速驶离公交站点的时间,系数ki(i=1,2,3,4)是因子Ti(i=1,2,3,4)对应的权重。
通过实际观察,我们发现在高峰时段,式(1)的参数T3主要受到乘客上车总人数P1、乘客下车总人数P2和公交车门关闭时间P33个约束条件的限制。因此,式(1)可以改写为公式(2):
DT=k1·T1+k2·T2+k3·(a1·P1+a2·P2+a3·P3)+k4·T4
(2)
式中:参数DT,ki(i=1,2,3,4)和Ti(i=1,2,4)定义与式(1)相同;ai(i=1,2,3)分别为乘客上车总人数P1、乘客下车总人数P2和公交车门关闭时间P3的权重系数。
我们使用F检验对不同站台环境下的公交停靠时间与因子Ti(i=1,2,3,4)进行统计性检验。其中,F检验的原假设为公交停靠时间与因子Ti(i=1,2,3,4)(其中,T3=a1·P1+a2·P2+a3·P3)不存在显著性关系,即系数ki(i=1,2,3,4)均为0,而备择假设为至少一个系数ki(i=1,2,3,4)不为0。这里,F检验的显著性水平为0.05,同时,我们也利用相关系数R2评价公交停靠时间回归模型与实测交通数据的吻合程度。
为了进一步验证构建的公交停靠时间模型与实测公交数据不存在明显的差异性,我们还利用了χ2检验方法统计分析公交停靠时间模型与实测交通数据的显著性差异,χ2检验公式如式(3)。并利用均方根误差(RMSE)计算公交停靠时间模型的预测值与实际观测值之间的差异,如式(4)。
(3)
(4)
式中:A为实测的广义公交停靠时间;T为理论的广义公交停靠时间;xacti是第i个数据序列采集的广义公交实际停靠时间,而xpreti是模型预测的第i个数据序列的广义公交停靠时间。
2 实验结果
2.1 统计分析结果
我们利用采集的公交停靠数据和公交监控视频序列进行分析,分别得到了交叉口公交站点和干道公交站点的公交停靠时间统计指标分布,如表1和表2。表1的早高峰时段,公交车在交叉口公交站的平均停靠时间为62.9 s,其停靠时间大概是午高峰时段公交停靠时间的2倍。同时,早高峰的公交平均停靠时间比晚高峰公交停靠时间长11.8 s。这说明,早高峰时段公交出行需求明显高于午高峰和晚高峰时段。此外,通过交通监控视频发现早高峰时段的青年乘客较多,而这些青年乘客的出行目的地大多是公交站附近的写字楼。此外公交监控视频显示,乘客希望能够尽快乘坐到站公交车赶往目的地。因此,当公交车抵达车站时,乘客们会选择挤上公交车,这也延长了早高峰时段公交车停靠站台的时间。而午高峰时段,公交车的客流量明显小于早高峰时段。此外,午高峰时段乘客对公交出行的延误时间的容忍度要高于早高峰时段。因此,午高峰时段公交车平均停靠时间明显小于早高峰时段公交车平均停靠时间。同理,可知晚高峰时段公交平均停靠时间短于早高峰时段,而长于午高峰时段[14]。
表1显示早中晚高峰时段的公交平均停靠时间均处于95%的置信区间内,但是表1的公交停靠时间标准差显示出不同时段的公交出行需求各自的特点。早高峰时段公交平均停靠时间对应的标准差约为午高峰时段的80%,晚高峰时段的50%。这说明,早高峰时段乘客希望尽快乘坐公交,尽量减少公交出行延误。而午高峰和晚高峰时段,乘客愿意耗费更长时间乘坐公交出行。
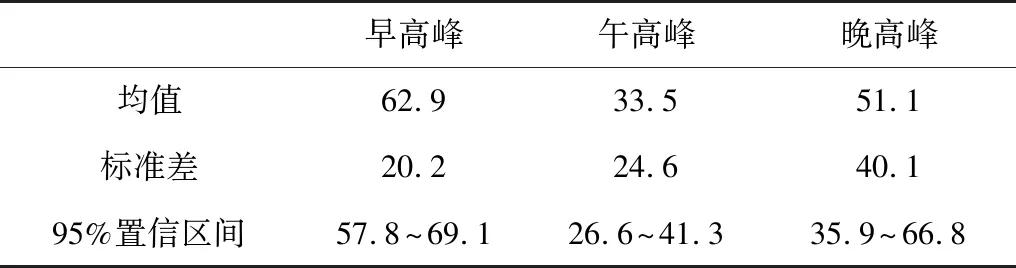
表1 交叉路口公交站的公交停靠时间统计指标Table 1 Statistical indicators of the bus dwell time at the bus stops at intersections s
表2的干道公交站点的公交停靠时间各项统计指标分布与交叉口公交站点的公交停靠时间分布类似。总体而言,公交车在干道公交站点的平均停靠时间短于其在交叉口公交站点的平均停靠时间。其中,早高峰时段,干道公交站点的公交平均停靠时间比交叉路口的公交平均停靠时间少10.1 s,这说明在交叉口的公交通行环境比干道交通通行环境复杂,交叉口环境下的公交通行效率会明显低于干道环境的公交通行环境,而表1和表2的午高峰和晚高峰公交停靠时间也验证了上述分析。表1和表2的各项公交停靠时间指标分布显示采集的交通数据用于评估、预测公交停靠时间分布具有统计显著性,因此,可以使用采集的交通数据对交叉口和干道等交通环境下公交停靠时间进行预测等研究与分析。
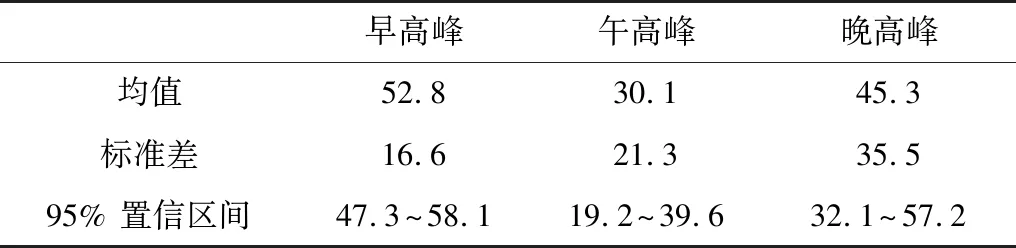
表2 干道公交站的公交停靠时间统计指标Table 2 Statistical indicators of the bus dwell time at the bus stops at the truck road s
2.2 回归分析结果
我们使用采集的数据序列对公交停靠时间统计模型的系数进行预测,将公式(2)对应的DT模型改写为式(5):
DT=f(T1,T2,P1,P2,P3,T4)
(5)
表3和表4为利用F检验统计分析交叉路口公交站点和干道公交站点的公交停靠时间统计模型系数的P值显著性分布表。根据统计学的相关知识,P值小于0.05则接受F检验的原假设,即公交停靠时间统计模型的系数不为0。表3和表4显示仅有P1和P2参数对应的P值均小于0.05,而其他参数P值均大于0.05,即式(5)中参数P1和P2对应的系数不为0,因此,式(5)简化为式(6):
DT=f(P1,P2)
(6)
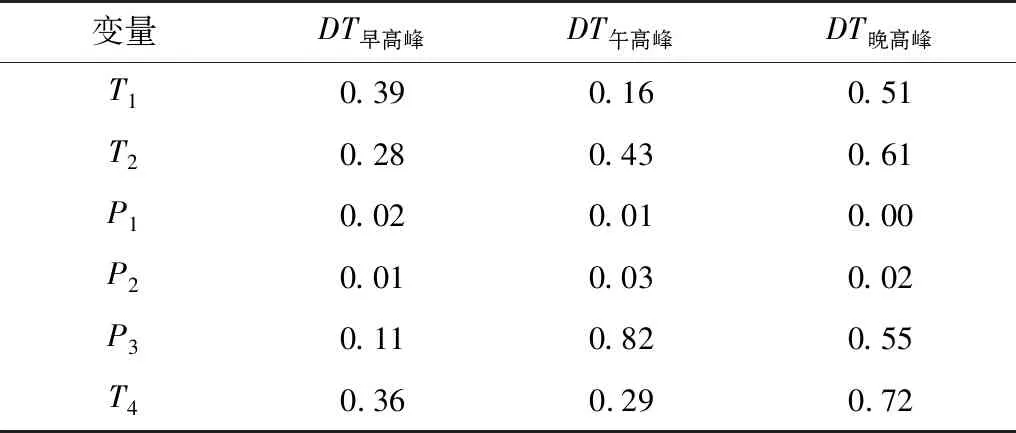
表3 交叉口公交站点的公交停靠时间统计模型系数的P值显著性分布Table 3 P-value significance distribution of statistical model coefficients of bus dwell time at the bus stops at intersections
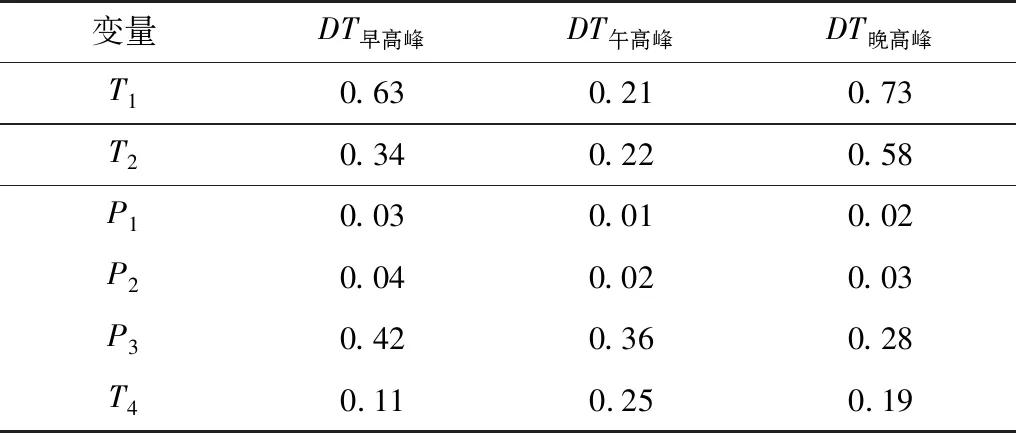
表4 干道公交站点的公交停靠时间统计模型系数的P值显著性分布Table 4 P-value significance distribution of statistical model coefficients of bus dwell time at the bus stops on the truck road
表5和表6分别是交叉路口公交站点和干道公交站点的公交停靠时间回归模型。其中R2表示参数系数的自相关性,该值越大,说明模型拟合效果越好。表5说明交叉口公交站点对应的R2值均大于0.8,这说明早中晚高峰时段DT模型的拟合结果与实测的交通数据非常接近。而且表5的P值均为0.00,这也验证了不同时段的DT模型与实测数据存在显著性关联。表5的RMSE说明实测数据与模型拟合数据之间的标准误差都处于较小的波动区间,说明DT模型的参数设置比较合理。表6中的R2值均大于0.85,这表明拟合的干道公交站DT模型能够较好地反映出实际公交停靠时间分布。此外,表6的P值与RMSE值均比较小,这也说明干道交叉口DT模型相关参数设置的合理性。
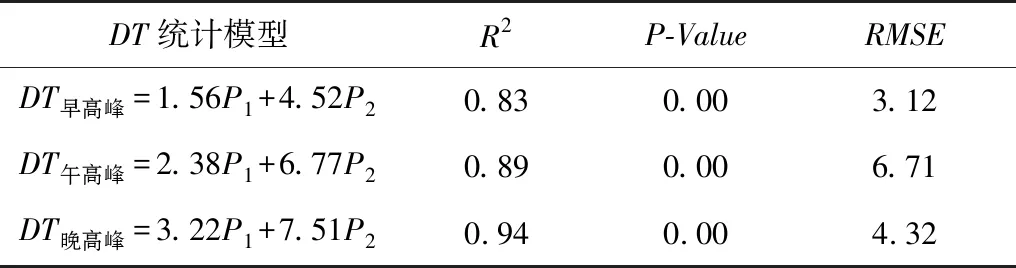
表5 交叉路口公交站点的早中晚高峰时段对应的公交停靠时间模型Table 5 The model of bus dwell time corresponding to the morning, middle and evening peak period at the bus stops at intersections

表6 干道公交站点的早中晚高峰时段对应的公交停靠时间模型Table 6 The model of bus dwell time corresponding to the morning, middle and evening peak period at the bus stops on the truck road
此外,为了进一步验证交叉口公交站和干道公交站DT模型的合理性,我们验证了这两种交通环境下的公交停靠时间模型系数显著性分布。表7和表8的P1和P2在不同时段,其相应的P值均小于0.05,这说明交叉口公交站和干道公交站对应的DT模型中,不同时段对应的参数P1和P2值均能够正确反映出该时段的公交停靠时间分布规律,这也说明DT模型设置的合理性。

表7 交叉路口公交站点的公交停靠时间模型系数显著性水平分布Table 7 The horizontal distribution of the coefficient significance of bus dwell time model at the bus stops at intersections

表8 干道公交站点的公交停靠时间模型系数显著性水平分布Table 8 The horizontal distribution of the coefficient significance of the bus dwell time model at the bus stops on the truck road
3 结 语
公交车在站台的停靠时间是城市公交线路服务可靠性的直接体现,也是评价城市公交系统服务水平的重要指标。考虑到现有方法主要利用乘客上下车的数量,公交车及公交站台长度,路边停车位数量等因素构建公交停靠时间模型,并没有过多考虑公交车站类型(靠近交叉路口的公交站和干道公交站)和不同时段乘客流量变化对公交停靠时间的影响。因此根据公交车站类型和不同客流时段构建新型的公交停靠时间模型。通过构建的公交停靠时间模型发现交叉口公交站点对应的最大公交停靠时间为早高峰时段,大约为63 s,晚高峰时段对应的公交停靠时间略短于早高峰时段,大约为51 s。午高峰时段公交停靠时间最短,约为34 s。而干道公交站点对应的最大公交停靠时间为52.8 s,晚高峰对应的公交停靠时间少于早高峰对应的公交停靠时间,为30 s。本研究成果表明,公交决策者可以采取各种措施减少早高峰时段公交停靠时间,并改善和提高公交调度规划和整体公交停靠站时间的可靠性。为了能够更好的分析公交停靠时间对道路等基础设施的影响,后期将结合新的交通环境提出新型的公交停靠时间模型,并比对不同公交停靠时间模型的有效性和可靠性。
——没有车的公交站

