粒料类基层沥青路面动力响应研究
高建红,许有俊,杨圣春
(内蒙古科技大学 土木工程学院,内蒙古 包头 014010)
0 引 言
我国现行的JTG D50—2017《公路沥青路面设计规范》[1](以下简称新规范)与2006版旧规范[2]相比,为路面结构组合提供了更丰富的选择,尤其针对我国90%以上的路面基层均为半刚性基层的事实,新规范认为为更有效地控制路面裂缝,在对待易裂的半刚性材料层时要多方面考虑、慎重选择。对于粒料类基层,文献[3]认为:其显著优点是无反射裂缝。同时新规范给出的4类基层材料中有两类为粒料类,由此预示了此类基层在以后路面结构中会越来越被重视、越来越被广泛采用。
针对车辆荷载动态加载下路面结构动力响应研究,学界大多数是采用静态模量。如李江等[4]通过建立有限元模型,分析了车辆以不同速度匀速通过和刹车状态下路面结构的动力响应;胡钢[5]针对层间接触的不同状态,分析了路面结构力学响应的变化规律;李星等[6]基于两种不同的有限元模型,分析了不同接触状态对弯沉、应力、应变的影响;周正峰等[7]针对不同沥青路面结构组合,分析了路基路面在不同轴载和轴型作用下的力学响应;邹静蓉等[8]分析了干线公路重交通等级沥青路面的破坏机理及控制措施;王旭东[9]针对静、动态模量两套模量体系对沥青路面弯沉的影响进行了深入阐释;邵财泉等[10]对比了材料静态与动态模量对路面结构设计的影响。也有部分学者采用动态模量进行动力分析,如黄兵等[11]分析了材料阻尼、荷载参数和层间接触等对沥青路面结构动力响应的影响规律。
基于以上分析,笔者结合结构动力学及振动理论,利用ANSYS/APDL软件,采用的材料参数为动态模量,建立了粒料类基层沥青路面的3D有限元模型;并分析了匀速移动的均布荷载和半波正弦荷载作用下路面结构的垂向应力及水平应力随时间变化的规律。以期为粒料类基层沥青路面在不同动载作用下的应力工况提供参考依据。
1 路面结构动力分析参数
1.1 结构和材料参数
路面结构以新规范中给出的粒料类基层基准路面结构组合为准;采用新规范中的重复循环半正矢脉冲荷载作用下的材料动态压缩模量。路面结构及材料参数取值如表1。
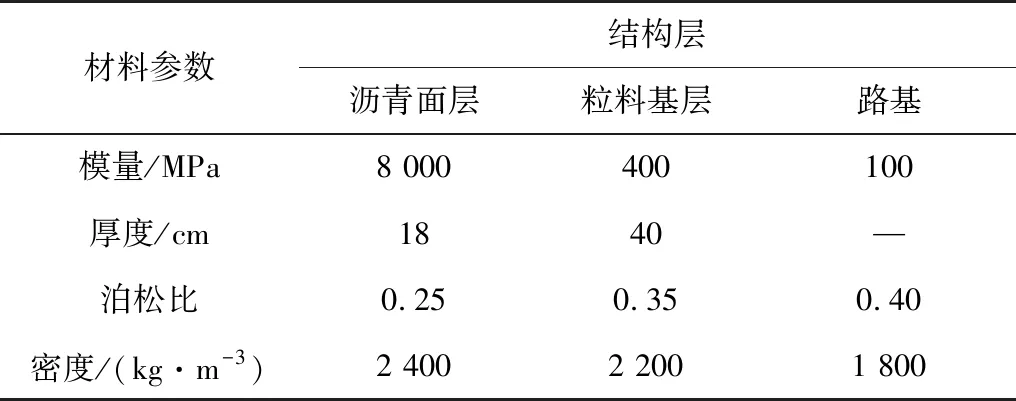
表1 路面结构及材料参数Table 1 Pavement structure and material parameters
路面结构阻尼采取Rayleigh阻尼形式,选取文献[12]中的路面结构阻尼比ζ=5%,α=2.690 7,β=0.000 9。文中土基采用弹簧单元模拟,不考虑此类单元的旋转性能,仅考虑其轴向性能,实常数按土基模量大小取值,即其轴向弹簧常数为1×108N/m,阻尼系数取为1×105N·S/m。
依据新规范,假定路面各结构层为连续均质、各向同性的线性弹性材料;路面各结构层在垂直方向完全连续;在交通荷载作用下产生下沉,层间不会出现脱空现象;沥青面层、基层之间为完全连续接触条件。
1.2 荷载参数
文中行车动载分两种情况:第一种为匀速移动的均布荷载;第二种为匀速移动的半正矢波荷载,又称半波正弦荷载。
均布荷载大小不随时间变化,始终为常量,如式(1):
P(t)=Pm
(1)
半正矢波荷载大小随时间变化,变化规律如式(2):
(2)
式中:P(t)为荷载随时间的分布,t为历时;Pm为荷载幅值,取标准轴载的静态压力,Pm=0.7 MPa;T为荷载作用周期,s;V为车辆行驶速度,m/s;δ为轮胎接地面积当量圆半径,m,标准轴载中双圆荷载δ=0.106 5 m。
文中设计车速为V=12.5 m/s=45 km/h。依据式(2),当V=12.5 m/s时,T=0.102 24 s。
1.3 模型参数
路面结构动力响应有限元分析模型尺寸若选取过小,会引起较大计算误差,尺寸过大又会占据过多计算机内存,使得运行速度变慢。笔者通过试算,确定不包括土基在内的沥青路面结构建模尺寸为6.0 m×10.0 m×0.6 m(X、Z、Y),计算模型如图1、2。
建模采用的单元分为4种:模拟土基弹簧单元COMBIN14;构成三维实体结构的六面体8节点等参元SOLID45;建立二维实体结构模型的面单元PLANE42;施加面荷载需要的表面效应单元SURF154。
边界条件假设为:底层弹簧全约束,即UX=UY=UZ=0;行车方向即Z方向前后约束,即UZ=0;道路宽度方向即X方向的约束为UX=0。荷载采用规范规定的标准轴载-双轮组单轴轴重100 kN,轮压0.7 MPa。在工程设计中,车轮荷载简化为当量圆形均布荷载,但考虑到轮胎与路面间的印迹并非圆形,而是更接近于矩形,因此文中的有限元模型加载面积按矩形考虑,且按双轮组作用计算。为方便加载,结合荷载行驶区域内网格划分的尺寸,取满载时其当量轮胎接地矩形的边长为:长×宽=(0.28×0.20)m。
图1 荷载作用下的侧面模型Fig. 1 Side model under load
图2 模型受荷后的应力云图Fig. 2 Stress nephogram of the model after loading
2 路面结构动应力响应分析
模型中车辆行驶方向为Z向,道路宽度方向为X向,深度方向为Y向。为清楚展示动荷载在不同层位处的应力时间历程曲线,笔者从荷载所经条带内的中间区域不同深度处取出3个间距相等的点,如图3。其中:表面层为1~3点;面层底面为4~6点;基层中间位置为7~9点。分别读取这些点在半波正弦荷载和均布荷载作用下的各类应力,绘制应力时程曲线并相互对比,可清晰观察不同加载方式下、不同位置处观测点的应力随时间的变化规律。应力方向定为:拉为正、压为负,单位为统一的国际单位制。
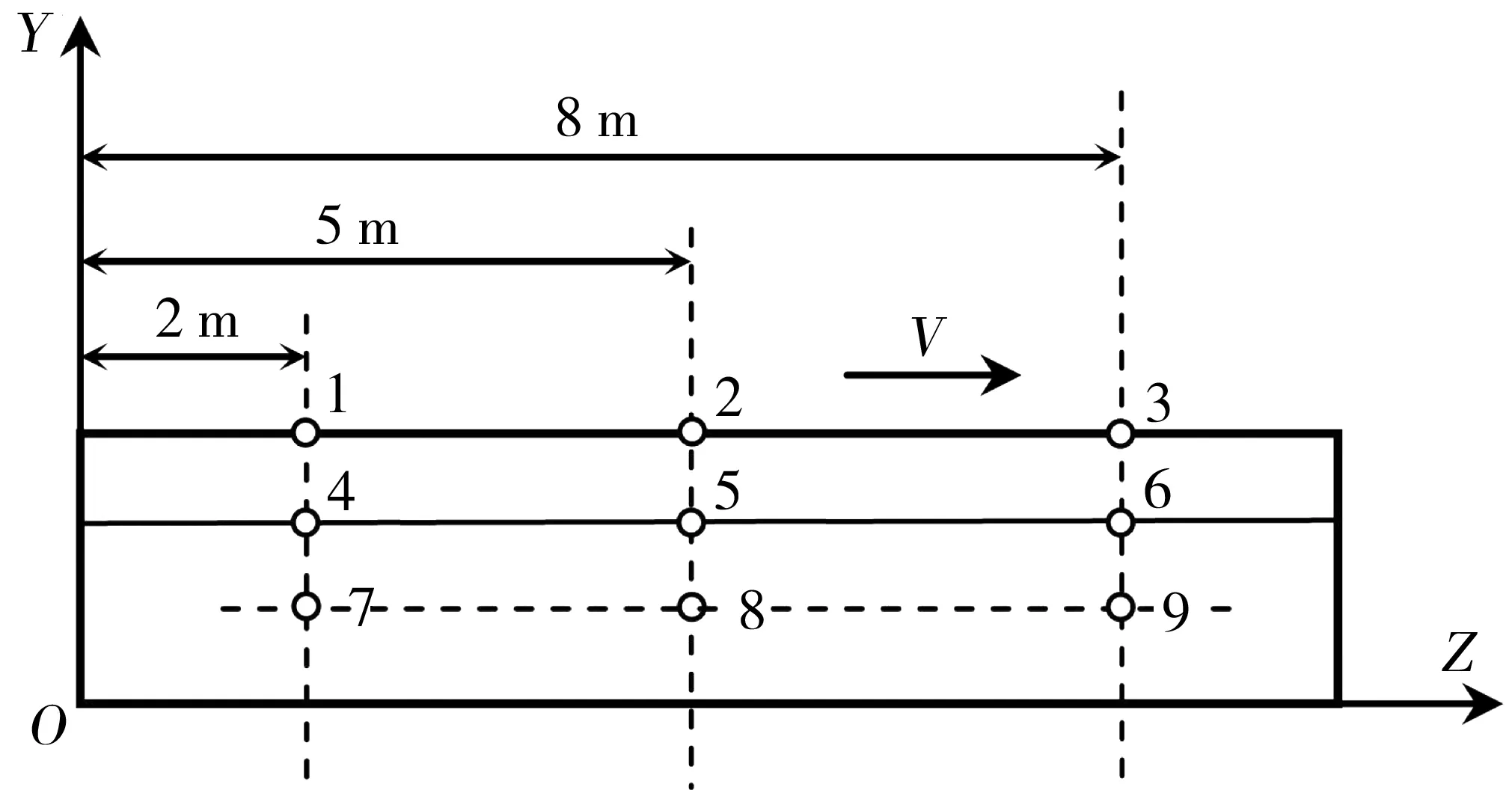
图3 模型中观测点分布示意Fig. 3 Distribution of observation points in the model
2.1 垂向应力动态响应规律
由表2可见:路表向下不同层位所受垂向应力均为压应力,拉应力非常小,可忽略不计。
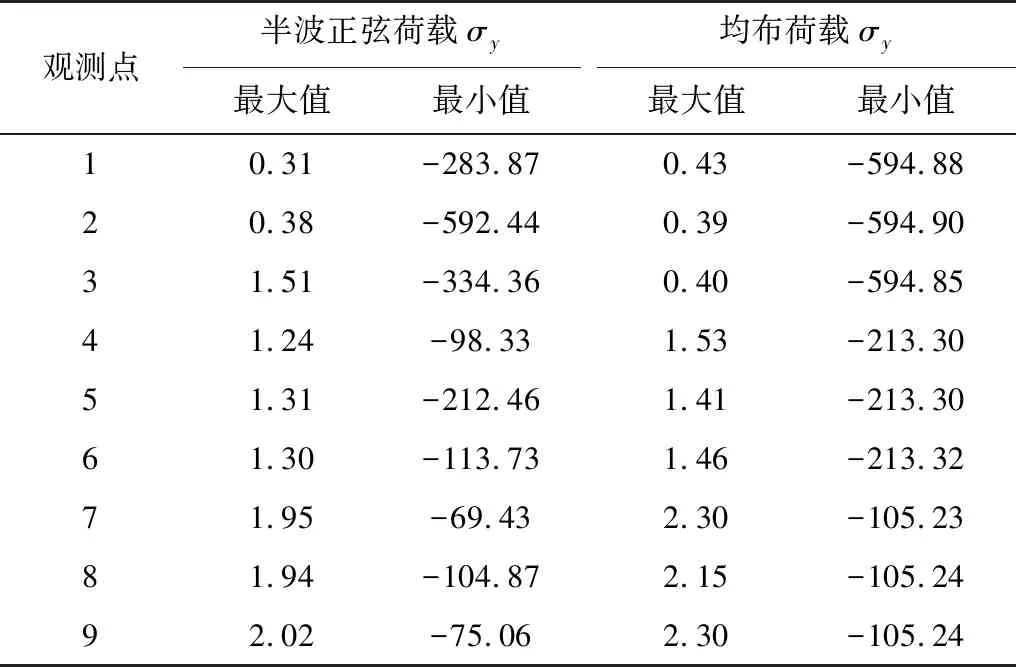
表2 两种加载方式下的垂向应力极值Table 2 Extreme value of vertical stress under two loading modes kPa
图4(a)为表面层1~3这3个点在半波正弦荷载和均布荷载作用下的垂向应力随时间的变化曲线。图4(a)中:在两种加载方式下,荷载到达点位之前该点垂向应力迅速增大,荷载行驶到点位时该点垂向应力达到最大值,荷载离开点位之后该点垂向应力迅速减小直至恢复为0,曲线看上去呈细长尖角状。图4(b)、(c)中:曲线形状逐渐趋向宽扁状,说明越向下,垂向应力峰值越小,且应力越扩散,观测点对车轮荷载的感应越滞后。
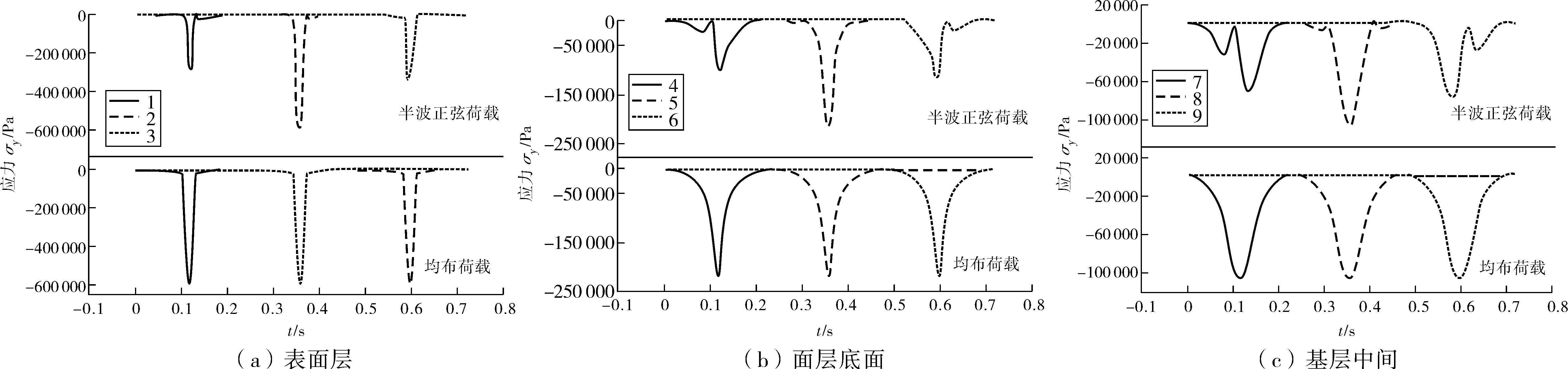
图4 垂向应力时程曲线Fig. 4 Vertical stress time-history curve
2.2 纵向水平应力动态响应规律
由表3可见:表面层和面层底面所受纵向水平应力有拉有压,基层中间位置所受应力几乎全部为压,拉应力很小接近于0。
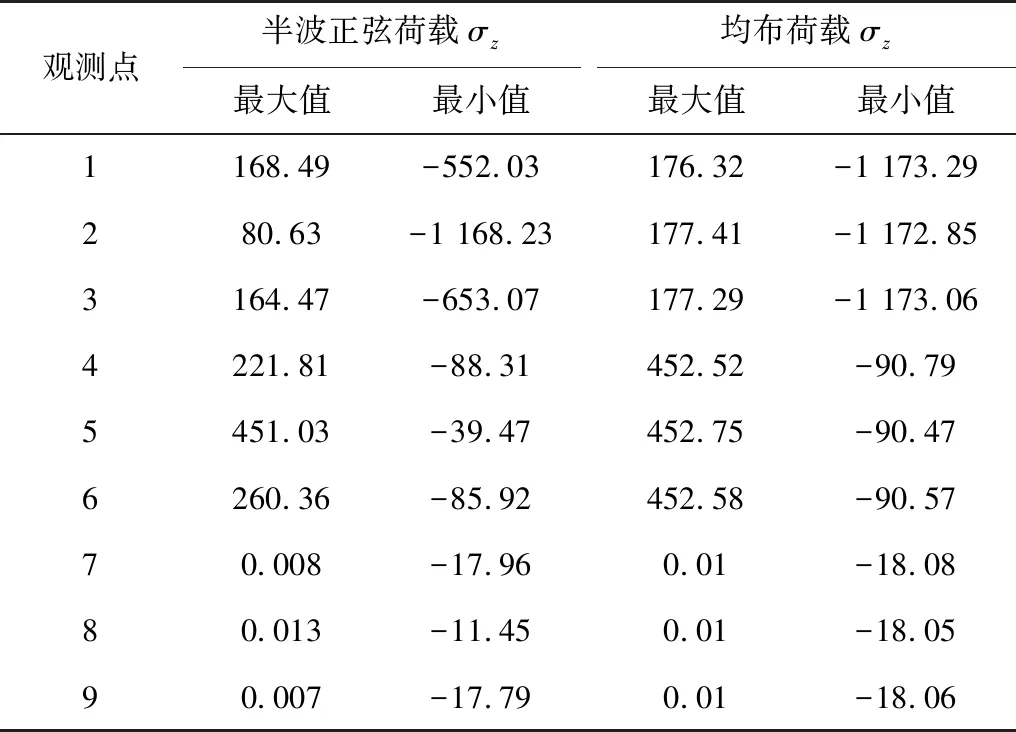
表3 两种加载方式下的纵向水平应力极值Table 3 Extreme value of longitudinal horizontal stress under two loading modes kPa
由图5(a)可见:此层位处的观测点受到较大压应力,较小拉应力;在两种加载方式下,移动荷载在接近点位时,该点受到较小的拉应力作用,到达该点时变为迅速增大的压应力,压应力增大到峰值后又迅速减小为0继而转化为较小的拉应力,然后随着移动荷载远离,该点应力恢复为0。由图5(b)可见:此层位处观测点受到较小压应力,较大拉应力;在两种加载方式下,移动荷载在接近点位时,该点受到较小的压应力作用,到达该点时变为迅速增大的拉应力,拉应力增大到峰值后又迅速减小为0继而转化为较小的压应力,然后随着移动荷载远离该点应力恢复为0。由图5(c)可见:此层位处观测点均受水平压应力;在两种加载方式下,移动荷载在到达点位前和离开点位后出现了两次比荷载位于点位处大得多的水平压应力峰值,且半波正弦荷载作用下的曲线起伏相比均布荷载有显著不同。
2.3 横向水平应力动态响应规律
由图6和表4可见:表面层和基层中间位置观测点主要受横向水平压应力,面层底面观测点主要受横向水平拉应力。在半波正弦荷载作用下,由于荷载波动特性及模型边界条件影响,模型长边方向靠近边缘的观测点,在荷载到达观测点之前会有小幅度曲线起伏,到达观测点时达到大幅度曲线起伏,同时曲线顶点达到极值。
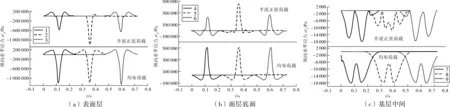
图5 纵向水平应力时程曲线Fig. 5 Longitudinal horizontal stress time-history curve
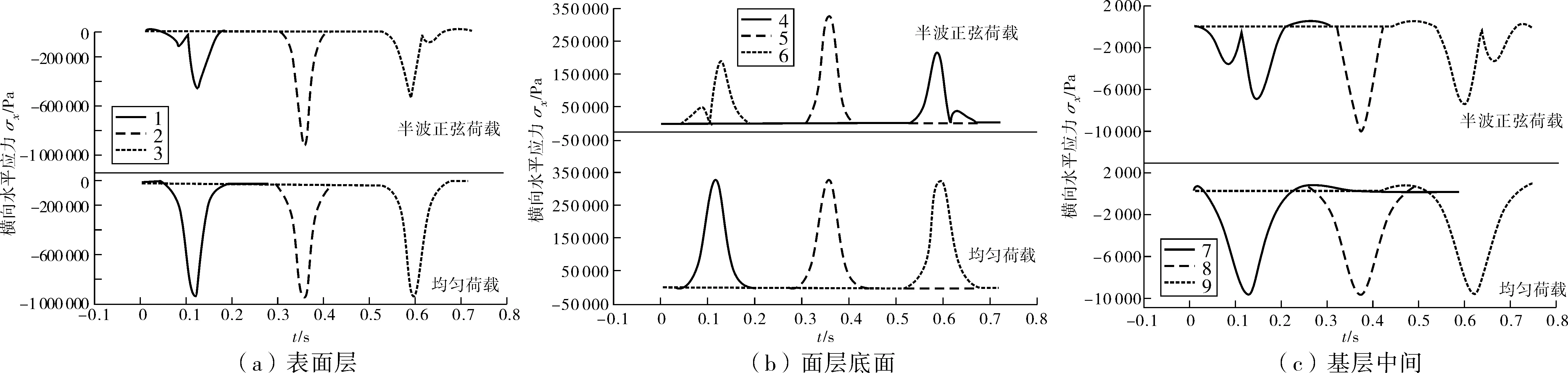
图6 横向水平应力时程曲线Fig. 6 Transverse horizontal stress time-history curve
由图4~6可见:在均布荷载作用下,不论观测点位于哪一深度处,这3点的应力时程曲线形状、峰值几乎完全相等;而在半波正弦荷载作用下,这3点应力时程曲线形状、峰值相差较大。而且观测的3个点位置越向下,两种加载方式下的应力时程曲线形状相差越大。究其原因,主要是半波正弦荷载大小随时间而变化,当荷载到达观测点时,可能荷载正处于峰值,也可能处于低值,或者处于某一中间值,因此得到的3个点垂向应力峰值就会不同;同时由于荷载的波动特性,使得半波正弦荷载作用下的应力曲线形状起伏多变。路表向下越深,观测点对加载反应越滞后,应力峰值越来越小,应力扩散作用更加明显,应力时程曲线形状表现为由表面细长尖角状逐步变化为较深位置处的宽扁状。
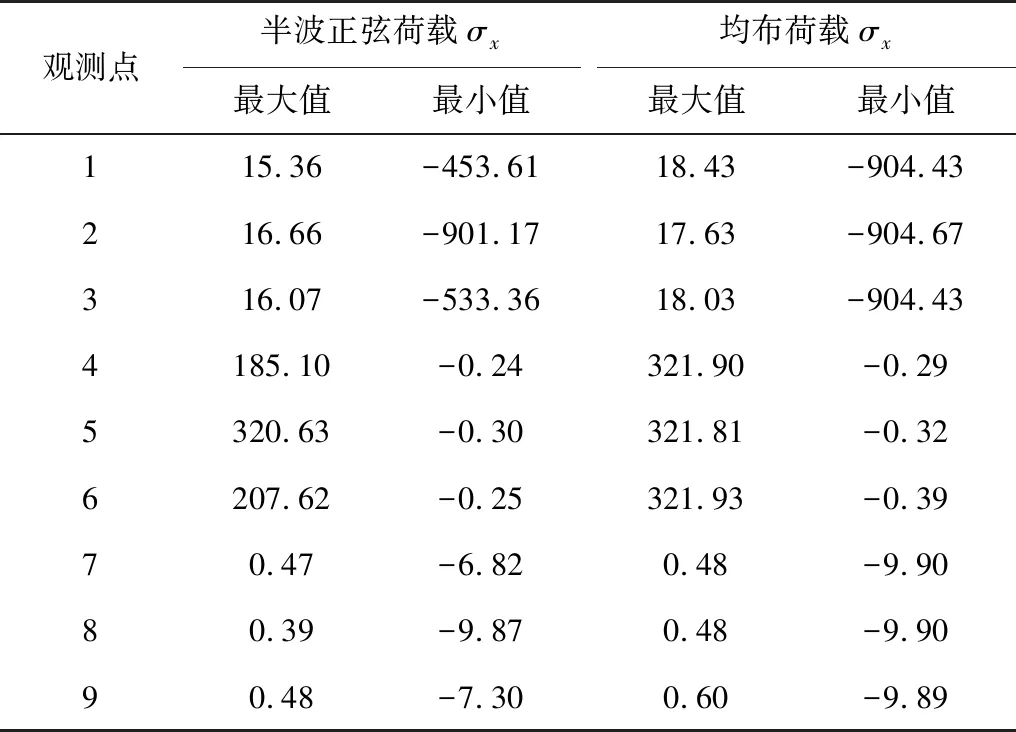
表4 两种加载方式下的横向水平应力极值Table 4 Extreme value of transverse horizontal stress under two loading modes kPa
综合表2~4可见:对表面层的3个观测点:最大垂向压应力为-595 kPa,最大纵向水平压应力为-1 173 kPa,最大横向水平压应力为-905 kPa;从数值上看,两类水平压应力的大小关系为:纵向大于横向。对面层底面的3个观测点:最大垂向压应力为-213 kPa,最大纵向水平拉应力为453 kPa,最大横向水平拉应力为322 kPa;从数值上看,两类水平拉应力大小关系为:纵向大于横向。对应基层中间处3个观测点:最大垂向压应力为-105 kPa,最大纵向水平压应力为-18 kPa,最大横向水平压应力为-10 kPa;从数值上看,两类水平压应力的大小关系为:纵向大于横向。垂向压应力由上至下逐渐减小。
3 结 论
1)由于半波正弦荷载的波动性,使得同一深度处半波正弦荷载作用下的3点应力时程曲线形状、峰值相差较大,而均布荷载作用下的3点应力时程曲线形状、峰值几乎完全相等,但两种加载方式得到的应力极限值基本相同。
2)不论哪种加载方式,路表向下越深,应力峰值越小,应力扩散作用越强,观测点对荷载作用的反应越滞后,表现为应力时程曲线形状由细长尖角状逐步变化为宽扁状。
3)垂向应力,不论处于哪一深度,总是压应力,且路表最大,路表向下越深,数值越小;纵、横向水平应力,由路表到基层,有压有拉,但总是纵向水平应力大于横向水平应力。

