一元一次方程易错题归纳
文 陈 桃
同学们学习一元一次方程时,常因知识点掌握不牢、解题粗心等原因出错。现将这部分内容中易犯的三种典型错误剖析如下,希望同学们引以为戒。
一、概念出错
例1 下列方程中,是一元一次方程的是( )。
A.2πr=6.28 B.x-y=7

【错解】D D。
【剖析】选项B中含有两个未知数x,y,所以不是一元一次方程;选项C中的方程虽然只含有一个未知数,但未知数次数为2,所以不是一元一次方程;选项D中的方程分母上有未知数,不是整式方程,所以不是一元一次方程;选项A中π不是未知数,是常数,只有一个未知数r,未知数的次数为1,所以是一元一次方程。故选A。
【点评】一元一次方程的概念包含三个要点:(1)只含一个未知数;(2)未知数的次数为1;(3)整式方程。
例2 若关于x的方程(1-m)x||m+20=0是一元一次方程,则m的值为_____。
【错解】m=1。
【剖析】由题意得:
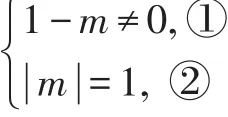
由①得:m≠1,
由②得:m=±1,
∴m=-1。
【点评】同学们仍然要抓住一元一次方程的概念。在一元一次方程中,如果未知数的指数或系数中含有字母常数,根据一元一次方程中未知数的指数等于1与未知数的系数不等于0,可以求得这个字母常数。
二、解法出错

【错解】①3(2x+1)-1=x-(10x+1),
6x+3-1=x-10x-1,
15x=-3,

②3(2x+1)-12=12x-10x+1,
6x+3-12=2x+1,
4x=10,

【剖析】解:去分母得,
3(2x+1)-12=12x-(10x+1),
去括号:6x+3-12=12x-10x-1,
移项、合并同类项:4x=8,
系数化为1:x=2。
【点评】解一元一次方程的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)未知数的系数化为1。这五个步骤在解一元一次方程中,有时可能用不全,有时可能重复用,也不一定按顺序进行。同学们要根据方程的特点灵活运用。
【归纳】易错点1:去分母时,漏乘不含分母的项;当分母是最简公分母时,忘记加括号。
易错点2:去括号时,若括号前是负号,括号里各项均要变号;括号里各项都要乘系数。
易错点3:移项忘记变号。
三、解含参方程出错
例4 当k取何整数时,关于x的方程2kx=kx+2(x+2)的解为正整数?
【错解】k=2。
【剖析】解:2kx=kx+2x+4,
2kx-kx-2x=4,
(k-2)x=4,

∵x为正整数,
∴k-2为4的因数。
∴①当k-2=1时,x=4;②当k-2=4时,x=1;③当k-2=2时,x=2。
∴k=3或k=6或k=4。
综上所述:k=3或4或6。
【点评】对于含参数的方程,我们一定要将方程先解出来。注意:只含参数的项移到方程右边作为常数,同时含参数和未知数的项移到方程左边,确保合并同类项时不漏项,最后将方程的左边转化为以含有参数的代数式为系数的未知项,系数化为1时,两边同时除以系数,即x用含参数的代数式来表示。而要使结果为整数,通常右边的代数式中,分子为整数,那么分母必为分子的因数。
小试牛刀
请同学们试着求解:
当k取何整数时,关于x的方程2kx=kx+2(x+2)的解为整数?

