基于车辆-移动轨道耦合模型的列车碰撞爬车行为

杨 超，李 强，王 曦，王明猛

（1.北京交通大学机械与电子控制工程学院，北京 100044；2.西南交通大学牵引动力国家重点实验室，四川 成都610031）

列车碰撞动态仿真通常采用有限元方法、多体动力学方法和有限元与多体联合仿真方法等[1-3].有限元方法与多体动力学方法相比各有所长.与有限元方法相比，多体动力学方法不能给出车体结构的变形.然而采用有限元方法进行单节车辆的碰撞仿真计算通常需要耗费数小时甚至几天的时间[4].文献[5]指出，采用36核的IBM工作站运行一个仅0.1 s的车辆碰撞仿真任务，消耗时间为29 h，占用磁盘607 GB.由此可见，非线性有限元软件模拟碰撞的计算成本很高.与此相对，多体动力学的计算速度极快，一般仅需要几分钟时间.因此在耐撞性车辆的前期设计阶段，多体动力学方法是首选的方法.

Lu用多体动力学方法研究了非线性条件下不同编组列车的碰撞，推导出列车碰撞能量配置计算公式[6-7].Dias和Pereira建立了简化的车辆碰撞动力学模型，用分段线性函数模拟车辆端部吸能部件，采用多目标优化方法为列车被动安全设计提供最佳设计参数[8-9].Sun等利用Gensys多体动力学软件建立了澳大利亚旅客列车的碰撞模型，在车辆端部分别设置高低吸能区，得到了列车的极限碰撞速度[10].卢毓江等提出并建立了一种考虑轨道模型的纵垂面车辆碰撞模型，为开展列车碰撞爬车和脱轨研究提供了基础[11].

列车碰撞研究中需要考虑车辆的纵向自由度.经典的车辆垂向统一模型[12]不考虑刚体的纵向自由度，主要用于研究轨道响应.本文侧重于车辆动态响应，主要研究列车碰撞爬车问题.轨道车辆碰撞爬车现象需要通过车轮抬升量或轮轨垂向相对位移评价，车辆重力主要靠轮轨垂向力平衡，因此轨道模型必须考虑到列车碰撞动力学模型中.集总参数式轨道模型可以适用于中低频的轨道动力响应问题[13]，足以胜任列车碰撞模拟工作.本文建立二维车辆-移动轨道模型，研究同型列车在直线轨道上发生低速正面碰撞，揭示车辆参数对列车碰撞爬车行为的影响规律.

1 列车碰撞建模

典型的列车碰撞场景是两同型列车正面相撞.如图1所示，主动列车以一定的速度V撞击非制动的静止列车.列车碰撞动力学模型由车辆模型、轨道模型（未画出）和车钩模型等组成.图2展示了红色虚线框内的模型细节.车辆-移动轨道耦合模型主要由二维的车辆模型和移动轨道模型组成，该模型基于经典的车辆垂向动力学模型，考虑了车体、构架和轮对的纵向自由度.纵向弹簧阻尼元件未在图中画出.平面内的自由度主要是纵向、垂向和点头自由度，文中分别用x、z和β表示.车辆-移动轨道耦合模型中，车辆模型具有17个自由度，轨道模型具有8个自由度，总计25个自由度.

图 1 列车碰撞模型Fig.1 Train collision model

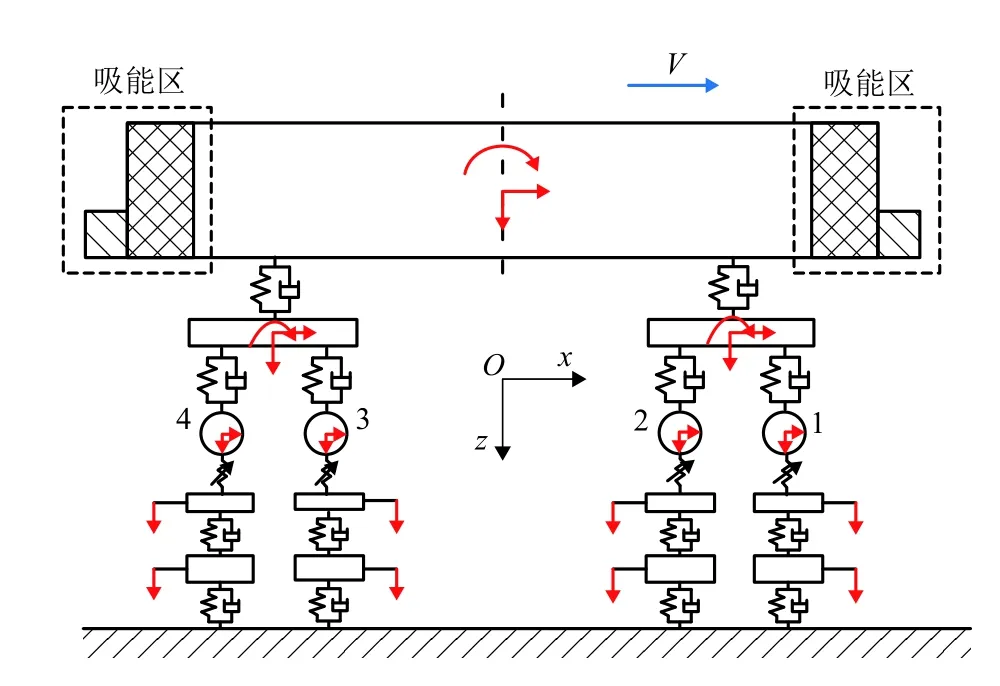
图 2 车辆-移动轨道耦合模型Fig.2 Coupled model of a vehicle and moving tracks

根据牛顿运动定律，列车碰撞动力学模型的运动方程可以写为

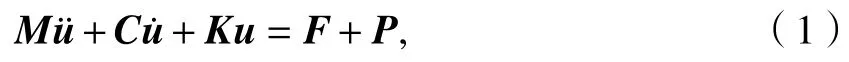
式中：M、C和K分别为运动系统的惯性矩阵、阻尼矩阵和刚度矩阵；、和u分别为加速度向量、速度向量和位移向量；F和P分别为外力向量和内力向量，P主要用于表示非线性的力向量，线性部分可以并入刚度矩阵或阻尼矩阵中.

1.1 车辆模型

车辆模型由轮对、构架、车体和悬挂系统组成.该车辆模型采用两级悬挂：轴箱悬挂包括一系弹簧、一系垂向减振器和轴箱定位装置等；中央悬挂包括二系弹簧、二系垂向减振器和牵引拉杆等.车辆的两端为无质量的吸能区，主要用于模拟车端结构和其他装置的吸能特性.鉴于低速碰撞情况，该车辆模型中不考虑防爬装置模型.

车辆模型中7个刚体，分别代表车体、构架和轮对.刚体之间通过弹簧和阻尼元件连接.车体和构架具有3个自由度，轮对不考虑旋转运动，仅有2个平动自由度，详细的自由度见表1.

表 1 车辆模型的自由度Tab.1 Degrees of freedom of vehicle model

车辆模型的运动方程与式（1）相同，方程中的矩阵是总体矩阵的子矩阵.其中，车辆系统的惯性矩阵是对角矩阵，刚度矩阵和阻尼矩阵都是对称矩阵.为了编程方便，此处给出车辆系统的惯性矩阵Mv、位移向量uv、外力向量Fv和阻尼矩阵Cv的表达式.

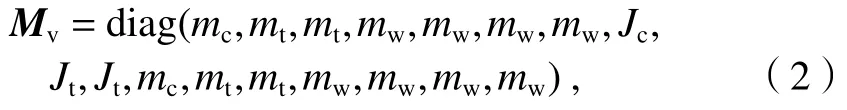
式中：mc、mt和mw分别为车体、构架和轮对的质量；Jc和Jt分别为车体和构架的点头转动惯量.

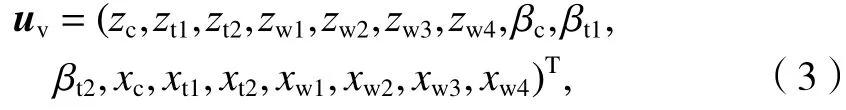
式中：zc、ztj和zwi分别为车体、构架和轮对的垂向位移，轮对编号i=1，2，3，4；βc和βtj分别为车体和构架的点头角位移，构架编号j=1，2；xc、xtj和xwi分别为车体、构架和轮对的纵向位移.

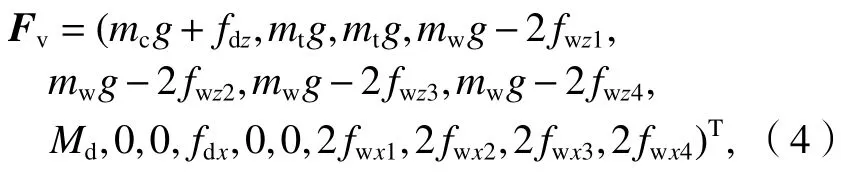
式中：fdx和fdz分别为车钩对车体的纵向外力和垂向外力；fwxi和fwzi分别为第i个轮对的单个车轮受到纵向轮轨力和垂向轮轨力，此处纵向轮轨力设为0；Md为车钩对车体点头的外力矩.

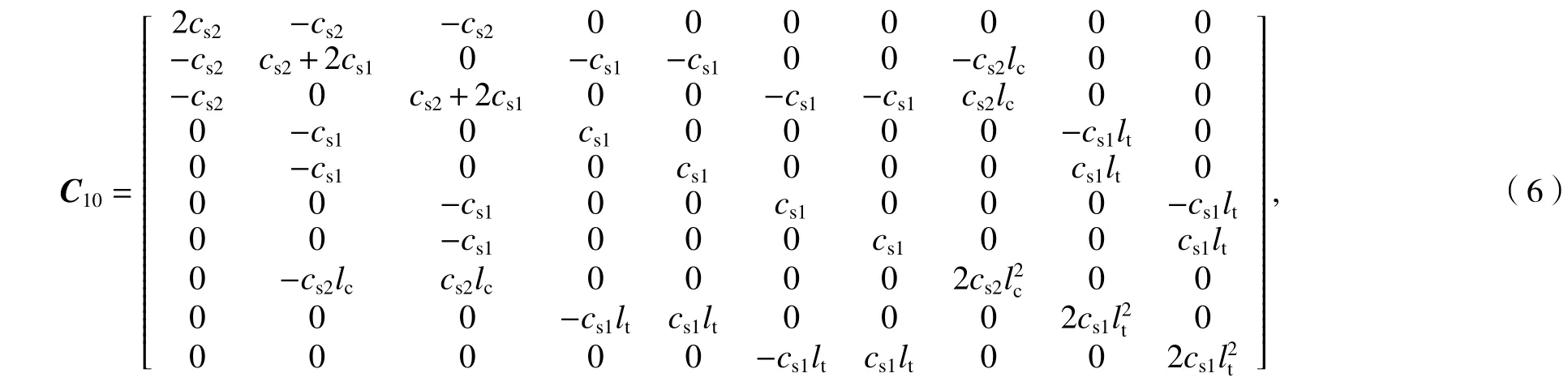
式中：C10为10 × 10对称阻尼矩阵；cs1为每个轮对的一系垂向阻尼；cs2为每个转向架的二系垂向阻尼；lc为车辆定距的一半；lt为转向架轴距的一半.刚度矩阵的前10阶方阵与式（6）具有相似的格式.

1.2 移动轨道模型

本文采用柔性的移动轨道模型[13]，轨道处于轮对正下方并随轮对一起纵向运动.模型中有8个刚体，分别代表数量相等的钢轨和轨枕，每个刚体仅有1个垂向自由度.钢轨扣件和橡胶垫用弹簧和阻尼元件模拟.相邻钢轨或轨枕之间没有关联.钢轨和轨枕的纵向自由度被强制约束，约束条件见式（7）.轨道模型自由度见表2.

式中：xri和xsi分别为第i个轮对下方的钢轨和轨枕的纵向位移.

根据文献[12]中的挠度和动能的等效原则可以计算得到各个部件的等效质量、等效刚度和等效阻尼.移动轨道模型的运动方程也具有与式（1）完全相同的格式，轨道的惯性矩阵Mr8、位移向量ur8和外力向量Fr8分别为

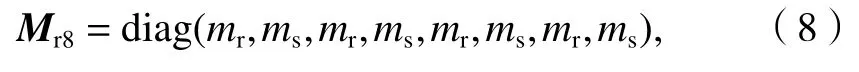
式中：mr和ms分别为钢轨等效质量和轨枕等效质量.

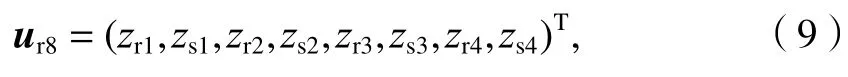
式中：zri和zsi分别为第i个轮对下方的钢轨和轨枕的垂向位移.

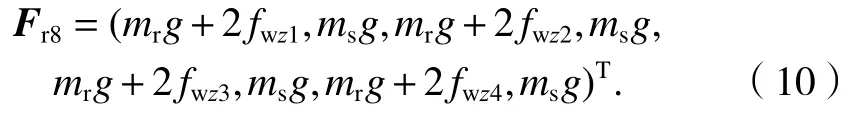
表 2 移动轨道模型的自由度Tab.2 Degrees of freedom of moving track model

2 非线性因素

2.1 轮轨垂向接触关系

列车碰撞标准中要求车辆碰撞时处于无制动状态，即不考虑轮轨的纵向摩擦力，因此假设钢轨在纵向是光滑的.对于不考虑轮对横向运动的车辆-移动轨道耦合模型，垂向轮轨力是主要的非线性环节之一.赫兹接触理论在轨道车辆动力学领域已经得到了广泛应用[12,14].根据赫兹弹性接触理论，第i个轮对的单个车轮受到的垂向轮轨接触力[12]为

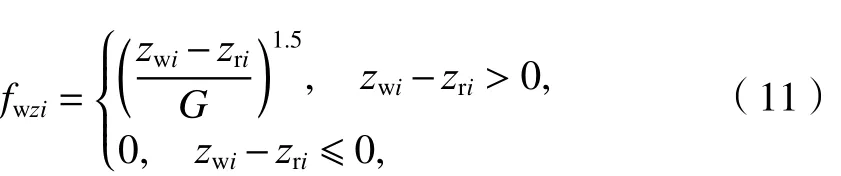
式中：G为轮轨接触常数，对于锥形踏面G=4.57R-0.149× 10-8m/N2/3，其中R为车轮滚动圆半径.

2.2 钩缓装置迟滞特性

在列车低速碰撞过程中不考虑钩缓装置的速度敏感性和失效.半自动车钩缓冲装置的主要吸能部件为缓冲器和膨胀式吸能管，缓冲器和吸能管具有复杂的非线性迟滞关系.为了方便处理，钩缓装置模型中集成了吸能管和缓冲器的输出特性.如图3所示，在压缩行程中，钩缓装置的轴向相对速度vd＜0，表示正在卸载，vd＞ 0，表示正在加载.当缓冲器达到最大行程时，吸能管开始作用，见图3中压缩加载曲线的水平段.当缓冲器和吸能管都达到最大行程并进一步压缩时，车钩与车体压死并出现刚性冲击，车钩力不断上升.钩缓装置在压缩行程中的车钩对车体的纵向外力为

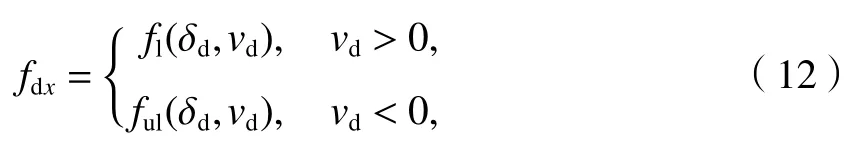
式中：fl（·）为钩缓装置的加载函数；ful（·）为钩缓装置的卸载函数； δd是钩缓装置的轴向相对位移.

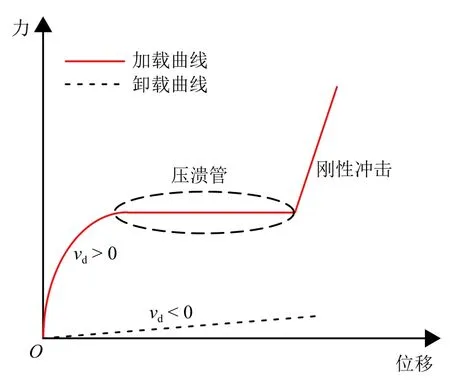
图 3 钩缓装置的压缩特性Fig.3 Compression characteristics of coupler device

式（12）不能处理零速度附近出现的车钩加载和卸载状态的相互转换.本文采用一种基于正则化速度判断状态转换的钩缓装置模型[15]，如式（13）.钩缓装置加卸载状态的转换靠正则化速度ve判断，ve的取值推荐为 0.001 m/s，当速度为（-ve，ve）时，车钩进入转换状态，利用线性插值得到加卸载状态的车钩对车体的纵向外力为

式中：fhys为缓冲器在某行程和速度下对应的迟滞力.

当不考虑车钩的阻尼特性时，简化的车钩加载和卸载函数仅仅与位移变化有关，分别为

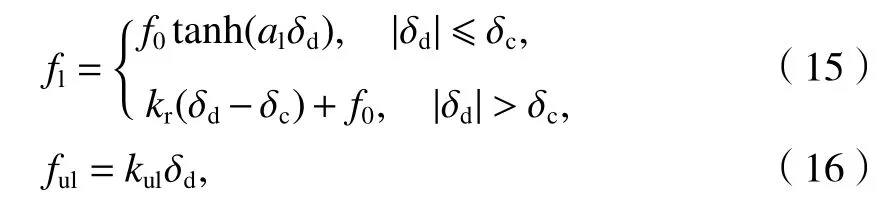
式中：f0为车钩吸能管的作用力；al为车钩的行程系数；kr为钩缓装置压死后与车体刚性冲击的接触刚度；δc为缓冲器行程与吸能管行程之和；kul为卸载曲线的斜率.

3 列车碰撞爬车行为的影响因素

在直线轨道上，8节编组列车以20 km/h的初速度撞击同型号静止列车.两列车的初始垂向偏差设置为0.碰撞爬车行为可以用车轮抬升量进行表征.根据EN15227标准[16]，转向架轮对的车轮抬升量不能同时超过轮缘高度的75%，至少保持一个轮对与轨道有效接触，此时可以认为车辆没有爬车风险.TB锥形踏面车轮的轮缘高度为25 mm，则车轮抬升量限值为18.75 mm.根据上述车辆、轨道、轮轨和钩缓装置模型，在MATLAB软件中编写列车-移动轨道模型的程序，程序已在文献[14]中经过基准测试.程序中的时间积分算法采用加速度显式法[17]，算法的积分参数为αjf= 1和γjf= 0.45.二维车辆模型和轨道模型参数见文献[12]，钩缓装置模型参数如表3.

本节研究碰撞速度、质心高度和二系垂向刚度对列车碰撞爬车的影响，分析这些参数关于车轮抬升量的灵敏度.车轮抬升量是静态和动态的垂向轮轨相对位移之差.静态情况下轮轨垂向压缩量是0.074 4 mm.如表4所示，各参数在给定初始值的基础上，按照一定的百分比放大.

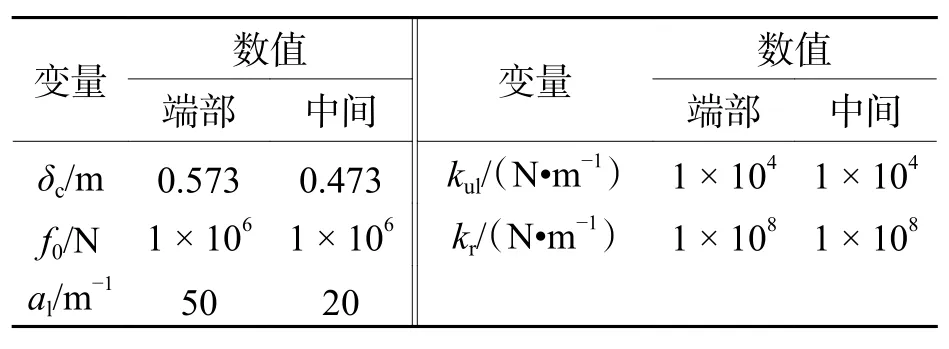
表 3 钩缓装置模型的参数Tab.3 Parameters of coupler model

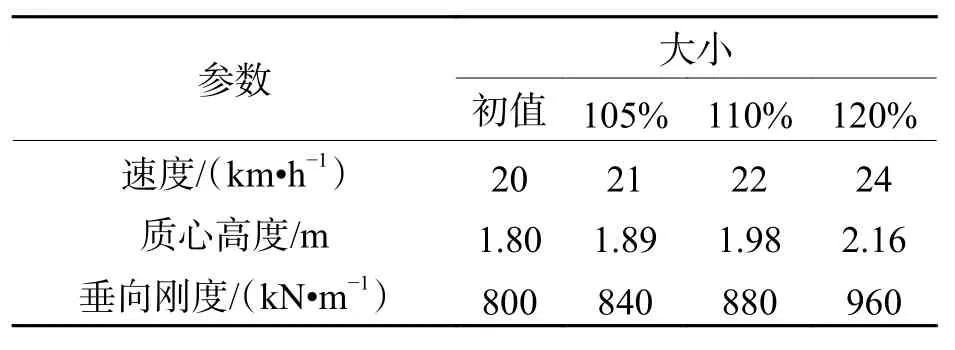
表 4 可变参数Tab.4 Variable parameters

3.1 车辆碰撞速度的影响

在不同碰撞速度下，选出车轮抬升量最大的轮对.图4给出了选中轮对的车轮抬升量随时间变化的情况.可以看出，在不同速度下，车轮抬升量都是先增大后减小，峰值都出现在1 s左右.车轮在下落阶段抬升量出现负值，垂向轮轨力比准静态的大.车轮抬升量峰值低于静态轮轨垂向压缩量.随着碰撞速度增大，车轮抬升量峰值出现延迟，车轮抬升量也逐渐增大.此外，当碰撞速度增大到27 km/h时，车轮抬升量陡增至36.5 mm，超过标准规定的限值，轮轨分离量较大，有爬车的风险.速度对列车碰撞爬车的影响很大.

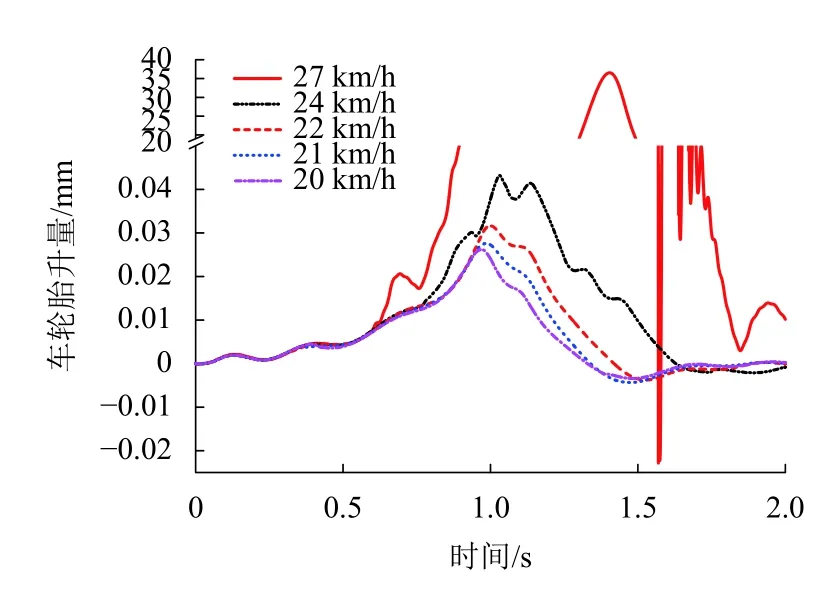
图 4 速度对车轮抬升量的影响Fig.4 Influence of impact speed on wheel lift

3.2 质心高度的影响

采用控制变量法，仅仅改变主动列车和被动列车的车体质心高度以及与质心高度相关的垂向距离，如车体质心到二系弹簧上平面的垂向距离等.不同质心高度下，车轮抬升量的时间历程曲线如图5所示.当质心高度增大20%时，车轮抬升量增加41%.当时间小于1 s时，车轮抬升量逐渐增大并达到最大值，然后逐渐减小.车轮抬升量峰值出现时刻随着质心高度增大而稍微提前.同样的，车轮抬升量峰值低于静态轮轨垂向压缩量.车轮抬升量随着质心高度增大而增大.

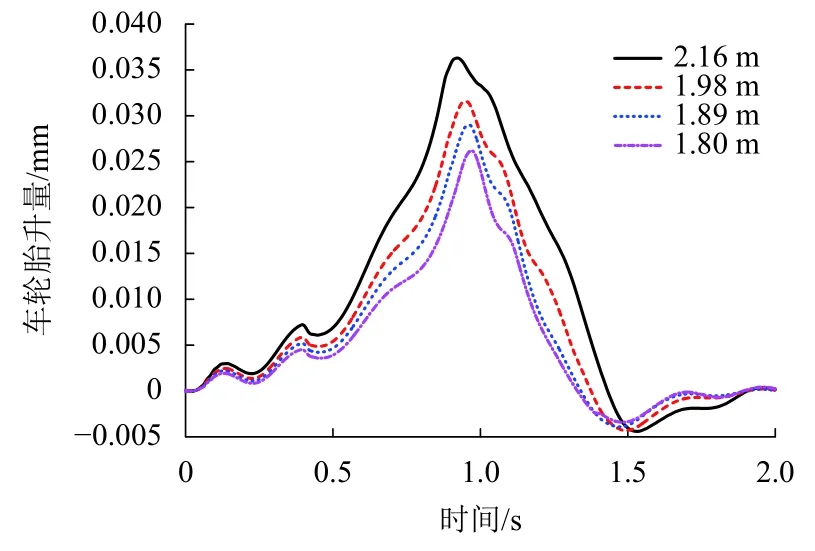
图 5 质心高度对车轮抬升量的影响Fig.5 Influence of heights of mass center on wheel lift

3.3 二系垂向刚度的影响

采用控制变量法，保持其他参数不变，仅改变列车的二系弹簧的垂向刚度.不同垂向刚度下，车轮抬升量随时间变化的曲线如图6所示.车轮抬升量在碰撞过程中先增大后减小，峰值也出现在1 s左右.整个碰撞过程中，车轮抬升量峰值比静态轮轨垂向压缩量小.然而，与碰撞速度和质心高度的效果不同，当二系垂向刚度增大20%时，车轮抬升量减小16.6%.随着二系垂向刚度的增大，车轮抬升量是逐渐减小的.

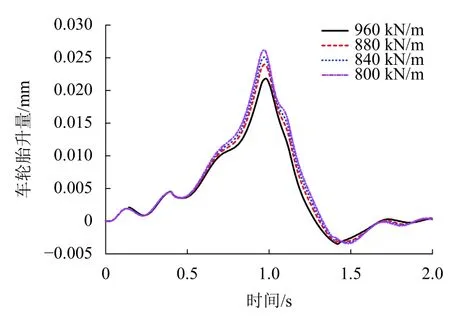
图 6 二系垂向刚度对车轮抬升量的影响Fig.6 Influence of vertical stiffness of secondary suspensions on wheel lift

3.4 灵敏度分析

为了量化碰撞速度、质心高度和二系垂向刚度对列车碰撞爬车的影响，采用车轮抬升量对参数的灵敏度和相对灵敏度衡量各个参数对车轮抬升量的影响程度.车轮抬升量灵敏度是车轮抬升量的增量与参数增量的比值.相对灵敏度是车轮抬升量变化的百分比与参数增大的百分比的比值.如图7所示，车轮抬升量对碰撞速度和质心高度的灵敏度是正的，而对二系垂向刚度的灵敏度是负的.车轮抬升量对碰撞速度的灵敏度是非线性的，并且速度对车轮抬升量的影响最大.车轮抬升量对质心高度和二系垂向刚度的灵敏度分别是2.87 × 10-2mm/m和-2.73 ×10-5mm/（kN·m-1）.车轮抬升量对参数变化的相对灵敏度如图8所示.相对灵敏度的数值等于图中曲线的斜率.质心高度和二系垂向刚度对应的相对灵敏度分别是205%和-83%.碰撞速度的相对灵敏度最大，且随速度增大而增大.由此可见，车轮抬升量对碰撞速度最敏感，对车体质心高度比较敏感，对二系垂向刚度是负敏感的.

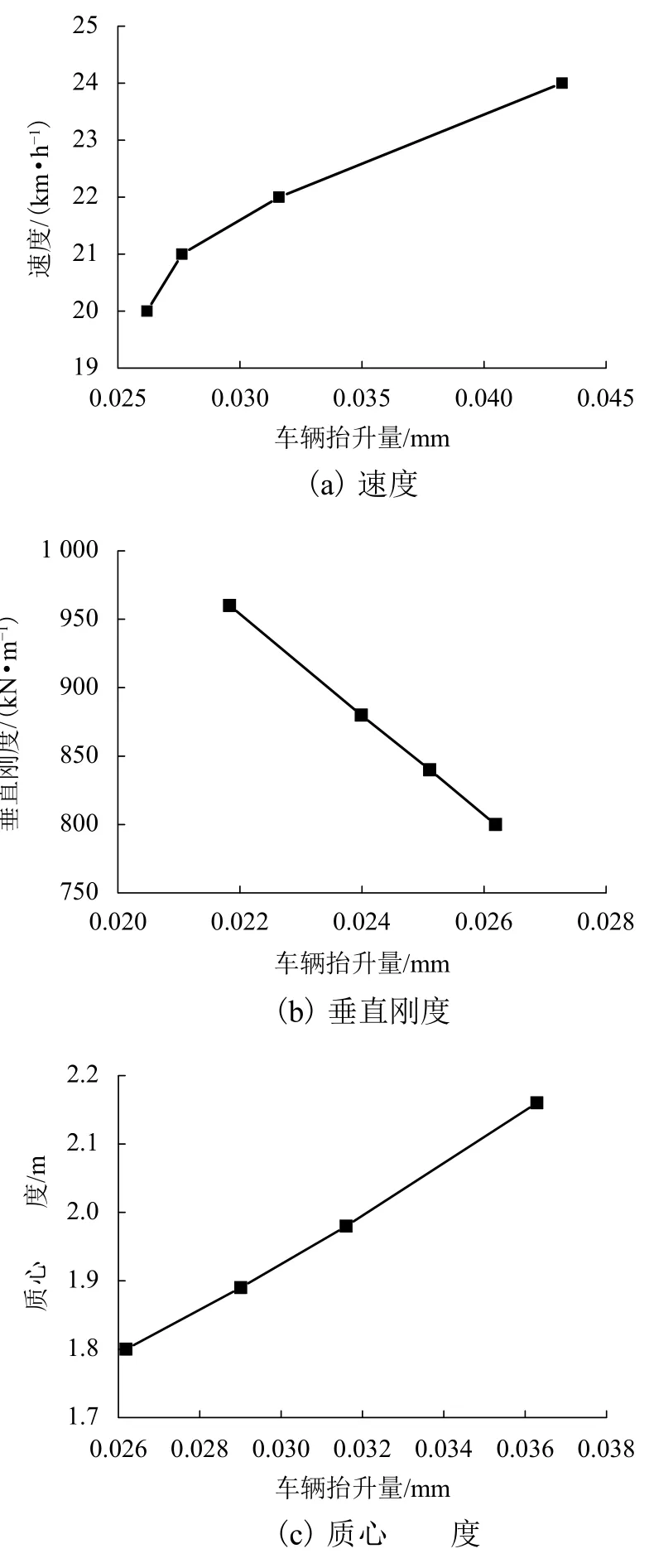
图 7 车轮抬升量对参数的灵敏度Fig.7 Sensitivity of wheel lift to vehicle parameters

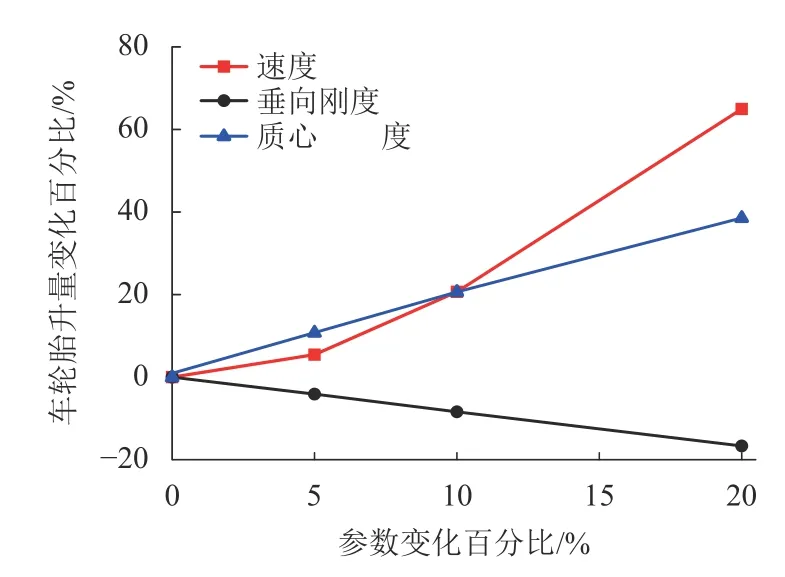
图 8 车轮抬升量的相对灵敏度Fig.8 Relative sensitivity of wheel lift

4 结 论

（1）在研究的参数中，碰撞速度对列车碰撞爬车影响最大.车轮抬升量随速度的增大而增大.车轮抬升量对碰撞速度的灵敏度是非线性的，且随速度增大而增大.

（2）车轮抬升量随着质心高度增大而增大.车轮抬升量对车体质心高度的灵敏度是正的，其值为2.87 × 10-2mm/m，相对灵敏度为205%.

（3）车轮抬升量随着二系垂向刚度的增大而减小.车轮抬升量对二系垂向刚度的灵敏度是负的，其值为-2.73 × 10-5mm/（kN·m-1），相对灵敏度为-83%.

列车碰撞爬车对碰撞速度最敏感，对车体质心高度比较敏感，对二系垂向刚度是负敏感的.采用二维车辆-移动轨道耦合模型研究列车碰撞爬车问题是足够的.然而，对于列车碰撞横向失稳行为，如碰撞脱轨和横向褶曲等，就需要构建更为详细的三维列车碰撞动力学模型.