列车荷载对板式无砟轨道力学性能的影响分析

任娟娟，邓世杰，闫亚飞，杜 威，倪跃峰

（1.西南交通大学高速铁路线路工程教育部重点实验室，四川 成都 610031；2.西南交通大学土木工程学院，四川成都 610031）

为减缓铁路运输压力，部分客运专线及既有线路采用了客货共线模式运营.由于无砟轨道具有高平顺性、高稳定性、良好的耐久性和少维修的特点，已在国内外高速铁路上得到了广泛应用，部分客货共线线路或者有砟轨道线路在隧道内也将无砟轨道结构作为行车基础[1-2].混凝土作为构筑无砟轨道结构的主要水泥基复合材料之一，具有组成复杂、多孔性、均质性差、极限应变小等特点，在客货共线铁路服役期内经客车荷载和货车荷载的长期反复作用下势必影响其损伤发展[3]，材料内部孔缝和界面区将发生演化，微裂隙、微空洞等的产生和演化将导致材料刚度退化、力学性能劣化.随着材料内部损伤的不断累积和发展，无砟轨道结构中出现了一系列典型伤损问题，笔者所在团队过去几年针对遂渝线蔡家车站以及赣龙线枫树排隧道线路段进行实地调研[4]，发现CRTS I型板式轨道的轨道板普遍存在开裂，裂开的轨道板在列车荷载以及环境的重复作用下又将进一步恶化.

就应力水平与加载频率对混凝土材料的疲劳性能和疲劳损伤的影响问题，国内外学者已做了大量的理论分析和试验研究.Van Ornum[5]最早开始混凝土抗压疲劳的研究，获取了最大应力水平为0.55的条件下，立方体和棱柱体混凝土试件单轴受压的疲劳寿命；Graf和Brenner[6-7]进一步的研究发现，试件的疲劳寿命均超过107次，且加载频率在4.5～7.5 Hz的范围内对混凝土疲劳寿命的影响较小；Marigo[8]建立了以孔隙为损伤参数的脆弹性材料疲劳损伤统一公式；Lacidogna等[9]利用声波检测法和动态识别技术，通过四点弯试验进行了与应力相关的损伤过程实现，同时考虑了混凝土梁固有频率的影响.马吉成等[10]从量纲的角度建立了包含加载频率的混凝土高周疲劳损伤方程，验证了1～6 kHz加载频率下的混凝土疲劳寿命.丁兆东、李杰[11]基于连续损伤力学，在细观尺度上建立了能量耗散公式，得到了疲劳损伤演化方程；卫军等[12]从混凝土材料的基本损伤机制出发，引入了残余变形因子，推导了混凝土疲劳荷载下的损伤本构方程；吕培印等[13]考虑累积损伤与损伤能释放率阈值，建立了循环荷载下的定测压双压疲劳损伤模型；Zhang等[14]通过弯曲试验研究了加载频率与应力水平对混凝土疲劳寿命的影响，得到了频率为 0.5、1.0、5.0、10.0 Hz和 20.0 Hz频率下，应力水平为0.8的工况下混凝土疲劳寿命的变化情况；杨俊斌等[15]通过有限元法建立CRTS I型板式无砟轨道弹性地基梁-体模型，研究了列车荷载作用下的疲劳损伤；朱胜阳等[16]基于连续损伤力学以及边界面的概念建立了高速铁路无砟轨道混凝土支承层在循环荷载下的疲劳损伤方程，但是均没有考虑列车荷载频率对无砟轨道材料损伤的影响.

以上研究成果大多关注于加载频率或应力水平对混凝土疲劳寿命的影响，鲜有对混凝土内部损伤和发展规律的试验研究.同时，现有的对混凝土疲劳性能试验研究的荷载与无砟轨道列车荷载的荷载特征值有较大差别，在无砟轨道领域中，列车荷载的频率分布范围相对较广，不能将以上的研究结果直接照搬，因此有必要针对列车荷载特征对无砟轨道混凝土结构进行循环加载试验，研究反复荷载对无砟轨道混凝土结构力学性能的变化规律影响.

1 损伤力学基本概念

在客货车荷载作用下，无砟轨道结构中混凝土内部损伤累积、缺陷演变、性能劣化是一个循序渐进的过程，传统的设计分析方法认为材料始终是完好无缺的，采用加大安全系数和偏于保守的破坏准则加以弥补.显然，这与现代无砟轨道工程结构设计和耐久性的要求是不相适应的.混凝土连续损伤力学通过引入一种损伤变量来描述含微观缺陷材料的力学效应和受损材料的力学行为，以便预测混凝土结构的变形、破坏和使用寿命[17]，损伤变量一般可以依据表观的物理量来间接量度.在材料中取出一微元体，定义其横截面积为A0，由于有损伤，用Ad表示受损部分的面积，于是A0-Ad表示实际横截面积，因此损伤变量

在初始横截面积上的Cauchy名义应力设为σ，由于损伤的存在，有效应力仅作用在未损伤面积A0-Ad上，其有效应力为

根据Lemaitre应变等效原理，任何受损伤材料在单轴或多轴应力状态下的变形状态都可以通过无损时的材料本构定律描述.于是含有损伤的材料本构关系为

式中：ε为材料应变；E0为初始弹性模量；Eda为材料受损后的弹性模量.

在伤损的状态下，Eda始终小于E0，说明材料弹性性能逐渐劣化.材料内部孔缝和界面区发生演化，将导致材料刚度退化、力学性能劣化，因此，损伤变量可以通过材料弹性模量以及强度的变化来表示.因为混凝土轨道板底部开裂是由板底拉应力超过极限拉应力造成，所以试验设置为弯曲动荷载试验，将抗弯强度作为损伤变量.

2 客货车荷载应力和频率设计

客货共线无砟轨道在服役期间承受着客、货两种特征值差异性较大的列车荷载，客车荷载作用频率高，产生应力较小，而货车荷载作用频率低，产生应力较大，因此在对客货共线运营条件下的无砟轨道混凝土力学性能研究时需要考虑这两种列车荷载的反复作用.由于1∶1原型试验难以模拟两种列车荷载的特征，并且不便于有效地测取混凝土力学性能变化的试验数据，故采用浇筑混凝土标准试件进行试验研究.因无砟轨道中混凝土结构与试验中混凝土梁试件的尺寸有较大的差异，在试验设计过程中需要把无砟轨道中的列车荷载转化为试件试验中的实际加载值.通过应力等效的原理使混凝土试件的最大应力值和无砟轨道结构中混凝土的最大应力值相等，以此确定试验荷载的加载幅值，确保试验工况能反映真实列车荷载下无砟轨道混凝土材料力学性能变化规律.故本文通过理论仿真来等效试验的加载工况，以明确试验中的荷载应力大小和加载频率.

为得到试验所用荷载应力水平，采用有限元法，以CRTS I型板式轨道为研究对象，主要考虑垂向列车荷载轨道板的应力分布情况，建立了如图1所示的以钢轨-扣件-轨道板-CA砂浆层-混凝土底座板-地基为主要结构的CRTS I型板式轨道力学计算模型.

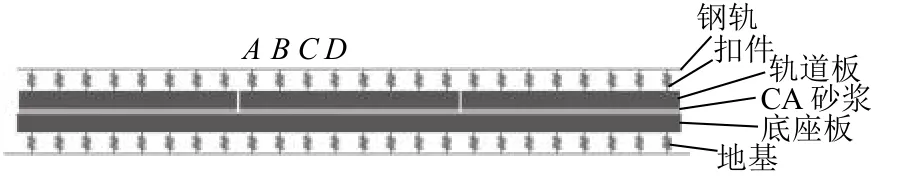
图 1 CRTS I型板式无砟轨道力学计算模型Fig.1 Mechanical calculation model of CRTS I slab track

模型总长为14.85 m（3块轨道板长），以中间轨道板作为研究对象.钢轨视为弹性点支撑梁并考虑重力作用，采用CHN60轨，弹性模量为2.1 × 1011Pa，泊松比为0.3，用BEAM188梁单元模拟.扣件系统采用COMBIN14线性弹簧单元，垂向刚度为6 ×107N/m.轨道板、砂浆层及底座板采用SOLID45实体单元进行模拟，弹性模量分别为3.65 × 1010、300、3.25 × 1010Pa，泊松比均为0.2.采用均布COMBIN14 线性弹簧单元模拟地基竖向支承，面刚度为75 MPa/m.理论计算中客车轮重取70 kN，货车轮重取125 kN，分别取静轮重、1.5倍静轮重以及3倍静轮重进行计算.在无砟轨道结构设计中，常用轮载取为1.5倍静轮重或150 kN（静轮重未知或客货共线时），设计轮载取为3倍静轮重或300 kN（静轮重未知或客货共线时）计算[18]，本文将货车荷载设为125 kN是处于偏安全设计考虑，以设计轮重作为最不利工况.根据计算得到不同荷载作用下图1的A、B、C、D处轨道板底最大拉应力，见表1.

表 1 轨道板底最大拉应力Tab.1 Maximum value of tensile stress at the bottom of track slab MPa

CRTS I型板式混凝土的强度为C60，其抗折强度kt不得低于 5.5 MPa，应力水平其中：σt为轨道板所受拉应力.

由表1可知：B处板底最大纵向拉应力最大，在1.0倍及1.5倍静轮重下的客车荷载对应的应力水平分别为0.14和0.22；货车荷载分别为0.26和0.40，而3.0倍静轮重的货车荷载对应的应力水平可以达到0.77，试验选取加载应力水平分别为0.3、0.5和0.7.

列车荷载的频率f为列车运行速度v和转向架固定轴距l（客车固定轴距为2.4 m，货车为1.75 m）的比值.

考虑试验设备的最大加载频率和列车荷载的实际运营速度，在试验中选取荷载频率分别为10、15、20 Hz，对应客、货车车速度见表2.

由表2可知：10 Hz荷载频率、0.3应力水平对应的客货车车速都低，低速列车荷载对轨道结构的冲击作用较小，混凝土在低速客车荷载作用下（取为1.0倍静轮重）应力水平很难达到0.3倍；货车荷载1.0倍静轮重有可能达到0.3倍应力水平，适用于模拟货车低速运营情况；15 Hz荷载频率、0.3应力水平，对于货车荷载车速较高，对轨道冲击较大，混凝土所受的应力水平大于0.3，而在此速度下，客车荷载下的混凝土所处应力水平可能达到0.3，所以可用于模拟客车低速运营；15 Hz荷载频率、0.5应力水平对于客车荷载的冲击作用很难达到，而货车可能达到0.5的应力水平，所以可用于模拟普速货车运营；根据表1的计算，加载频率15 Hz、应力水平0.7只有在货车3倍静轴重的情况下才会达到，所以模拟轮轨接触状态极差的普速货车最不利运营；根据表1计算结果，20 Hz荷载频率、0.3的应力水平，对应客车普速运营情况.综合客、货车轴重及运行速度，本文选择模拟不同条件下客、货车加载工况，如表3所示.

表 3 荷载组合模拟的车况Tab.3 Mombination of different stress levels and frequencies for train loads simulation

3 客货车荷载作用下混凝土棱柱体试件反复加载试验

为了分析CRTS I型板式轨道受列车荷载作用下轨道板的损伤变化规律，对混凝土试件进行反复加载试验模拟轨道板受列车荷载的反复作用情况.循环荷载依靠MTS系统施加，MTS加载系统以及试件的安装如图2所示.

图 2 循环加载设备Fig.2 Cycling loading equipment

按照普通混凝土力学性能试验方法标准[19]，浇筑了一批混凝土试件，根据混凝土标准力学试验规范对试件力学性能进行检验，得到混凝土试件抗折强度，如表4所示，计算出混凝土试件平均极限抗折强度为7.46 MPa.得出0.3应力水平对应的实际加载值为8.78 kN，0.5应力水平对应14.63 kN，0.7应力水平对应20.48 kN.

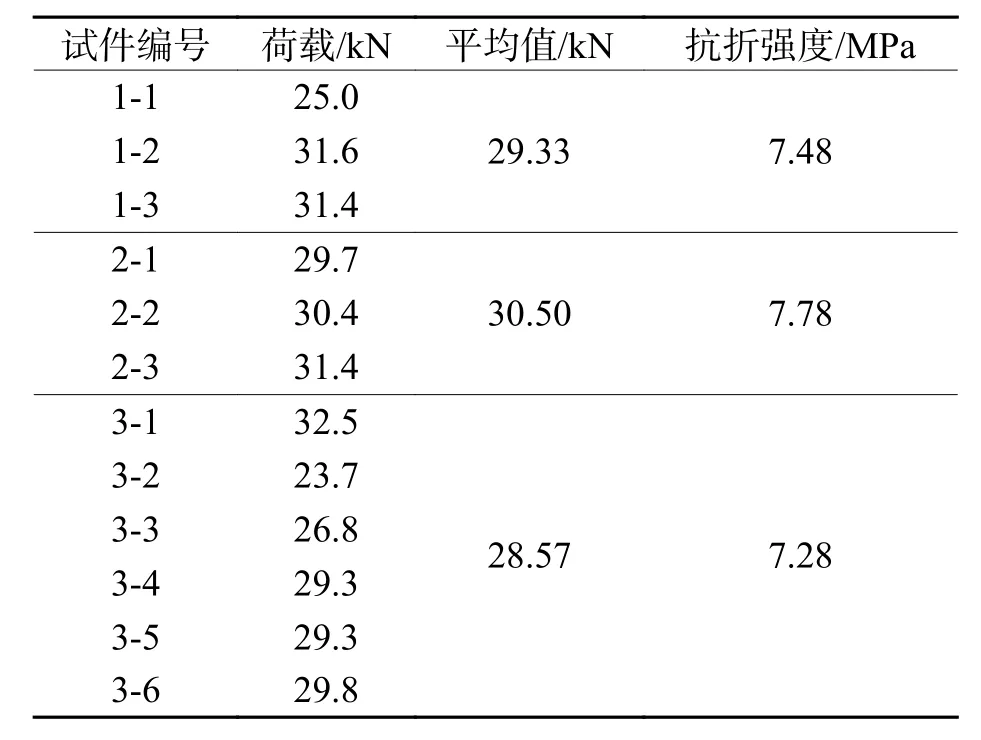
表 4 混凝土试件抗折强度Tab.4 Flexural strength of the concrete specimens

为测试同一试件在不同加载次数N下的弹性模量以及抗折强度，需多次采集数据，本试验基于无损检测系统，采用冲击弹性波法对混凝土动弹性模量和抗折强度进行检测.混凝土的弹性模量与激振时产生波的波速之间的关系经过大量理论与试验验证[20-21]，如式（3）.

式中：vp为纵波波速；vr为表面波波速；Eh为混凝土的动弹性模量；ρ为混凝土密度；v为泊松比.

由式（3）可知，只需测出vp和vr，便可计算出混凝土的动弹性模量.

超声波和弹性波的激振方式均由混凝土表面诱发振动产生，而冲击弹性波法无需测试混凝土回弹值[22].因此参照CECA02—2005《超声回弹综合法检测混凝土强度技术规程》中超声回弹综合法测定混凝土抗折曲线的通用式[23]，可推测弹性波测试混凝土抗折强度为

式中：a、b为待定系数；vp可由vp=βvc得出[24]，β为几何形状系数，其值与混凝土结构的厚宽比有关，本试验取为0.86，vc为用回归方法求取的波速值.

根据混凝土抗折强度测试和无损检测结果可得kt= 1.515v1.059.

4 混凝土材料力学性能衰减规律

通过试验探寻研究不同工况下混凝土动弹性模量以及抗折强度的变化规律，从而研究客、货车荷载作用对无砟轨道混凝土轨道板力学指标变化规律的影响.

4.1 混凝土力学性能变化规律

为了相互验证数据的正确性，5种工况都设置了两组试件，如表5所示，试验结果如图3，除加载频率为15 Hz，应力水平为0.7工况，其他工况2组试件存在类似的变化趋势，说明所测试的数据有效.

表 5 混凝土循环加载试验样本Tab.5 Concrete samples of cyclic loading test

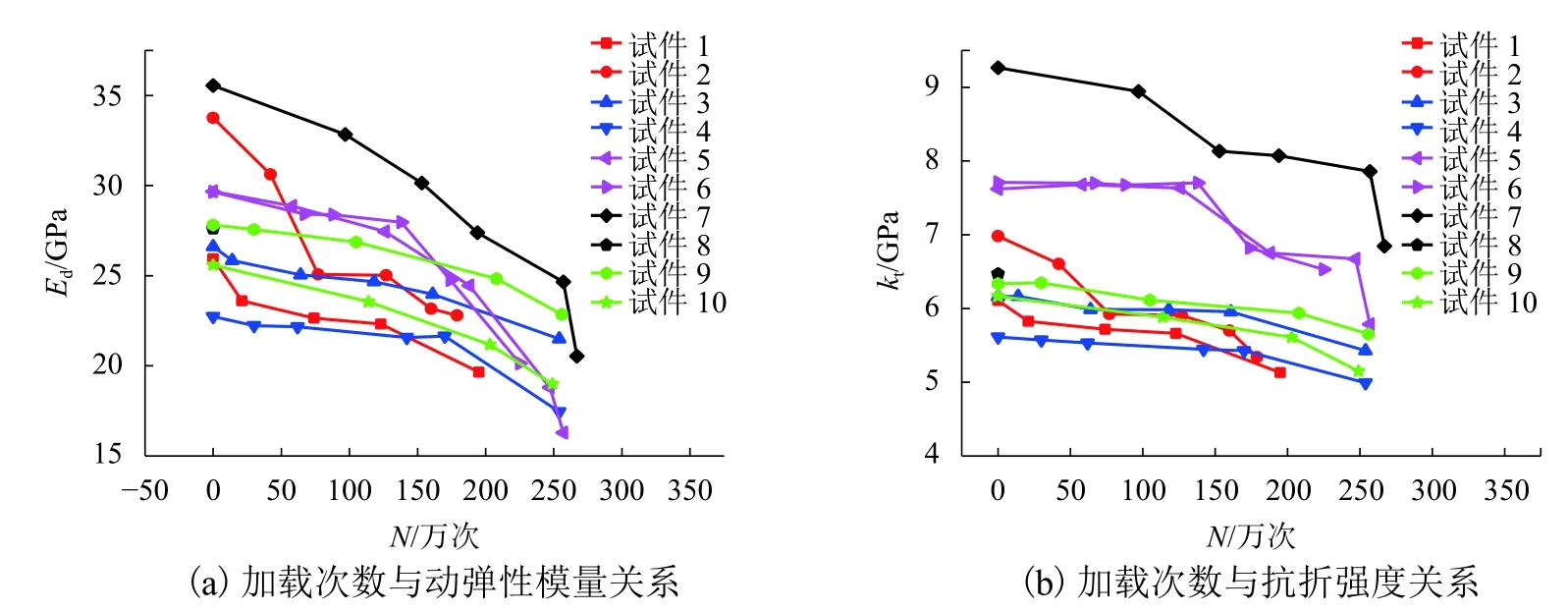
图 3 不同加载工况下混凝土力学性能衰减曲线Fig.3 Degradation curve of concrete mechanical property under various load conditions

由图3可以看出，混凝土力学特性的变化大致分为3个阶段：第1阶段，在承受荷载初期由于混凝土内部结构的微观缺陷导致应力集中产生微裂缝，使其宏观上的动弹性模量以及抗折强度衰减；第2阶段，由于裂纹扩展使得聚集在混凝土内部的能量得以释放，在荷载作用下能量达到了一种相对稳定状态，所以混凝土动弹性模量及抗折强度的衰减得以缓解；第3阶段，微裂缝扩展，内部缺陷加剧，相对平衡最终被打破，使其动弹性模量及抗折强度加速衰减.这与Alliche[25]、宋玉普[26]研究结果一致.

为减少材料本身因素引起的离散性，选择初始状态接近的试件数据来进行对比，根据图3选择试件 1、3、5、8、9 的数据.

4.2 频率对混凝土力学性能变化规律的影响

为表征混凝土试件具体损伤程度，根据第1节得到动弹性模量损伤变量dE= 1 -Ed/E0，在本试验中Ed表示不同加载次数下测试的动弹性模量.同理，定义混凝土抗折强度损伤变量dft= 1 -ft/ft0，其中ft0为初始抗折强度.

应力水平为0.3，加载频率分别为10、15、20 Hz的工况下，得到加载次数与混凝土损伤变化曲线，如图 4（a）所示.

由图4（a）可知：混凝土的动弹性模量以及抗折强度的损伤都随着加载次数的增加变大；当加载200万次时，加载频率为10 Hz的混凝土动弹性模量与抗折强度损伤较15 Hz和20 Hz大，分别为0.25和0.16；15 Hz工况下的混凝土损伤比20 Hz工况下损伤大，但是在加载100万次后，两条曲线逐渐靠近，说明加载后期20 Hz工况下混凝土动弹性模量损伤程度有超过15 Hz工况下的混凝土损伤的趋势；抗折强度差距较小，15 Hz工况下的混凝土抗折强度损伤程度在加载100万次之前以及170万次后，大于20 Hz工况下的损伤；在加载100万次～170万次左右，20 Hz工况下的损伤程度大于15 Hz工况下的损伤程度；在混凝土的损伤第1阶段与第3阶段均为15 Hz工况下的损伤程度大于20 Hz工况下的损伤；200万次加载后，加载频率越小，混凝土动弹性模量以及抗折强度的损伤程度越大，并且在10～15 Hz之间较明显；同一试件，动弹性模量的损伤程度比抗折强度的损伤程度大.

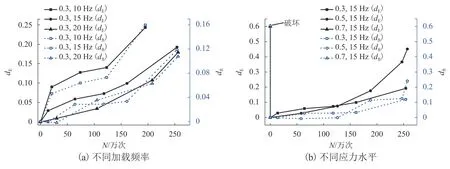
图 4 混凝土力学性能变化规律Fig.4 Degradation curve of concrete mechanical

4.3 应力水平对混凝土力学性能变化规律的影响

取加载频率为15 Hz，应力水平分别为0.3、0.5和0.7工况下混凝土试件测试数据，在测试应力水平为0.7的工况时，试件在1 000次循环荷载下遭到破坏，以动弹性模量和抗折强度损伤0.6为破坏准则[27]，得到加载次数与混凝土动弹性模量以及抗折强度变化曲线如图4（b）所示.

由图4（b）可知：当加载频率一定时，应力水平为0.7工况下混凝土动弹性模量和抗折强度下降最快；在循环荷载1 000次作用下混凝土试件便发生破坏，在150万次荷载作用后0.5倍应力水平明显比0.3倍应力水平的动弹性模量损伤以及抗折强度损伤大；加载频率一定，应力水平越大，混凝土动弹性模量以及抗折强度的损伤越严重，并且混凝土的动弹性模量损伤程度比抗折强度的损伤程度大.

由于应力水平0.7为列车荷载最不利工况，在试验中测试了几组数据作参考，如表6所示.其中，4个试件有3个在1 000次以及2 000次循环荷载下遭到破坏，说明应力水平0.7加剧了混凝土动弹性模量及抗折强度的衰减.从强度方向看，应力水平0.7的荷载是根据平均抗折强度的0.7倍施加，而混凝土试件平均抗折强度为7.46 MPa，所以MTS系统施加的荷载对应为0.7 × 7.46 = 5.22 MPa.试件1的初始抗折强度为9.27 MPa，其加载实际应力水平为5.22/9.27 = 0.56，其他3个试件的初始抗折强度接近7.46 MPa，对应的应力水平约为0.7.因此3个已破坏的试件才是反映应力水平为0.7的工况下混凝土动弹性模量及抗折强度的变化规律.

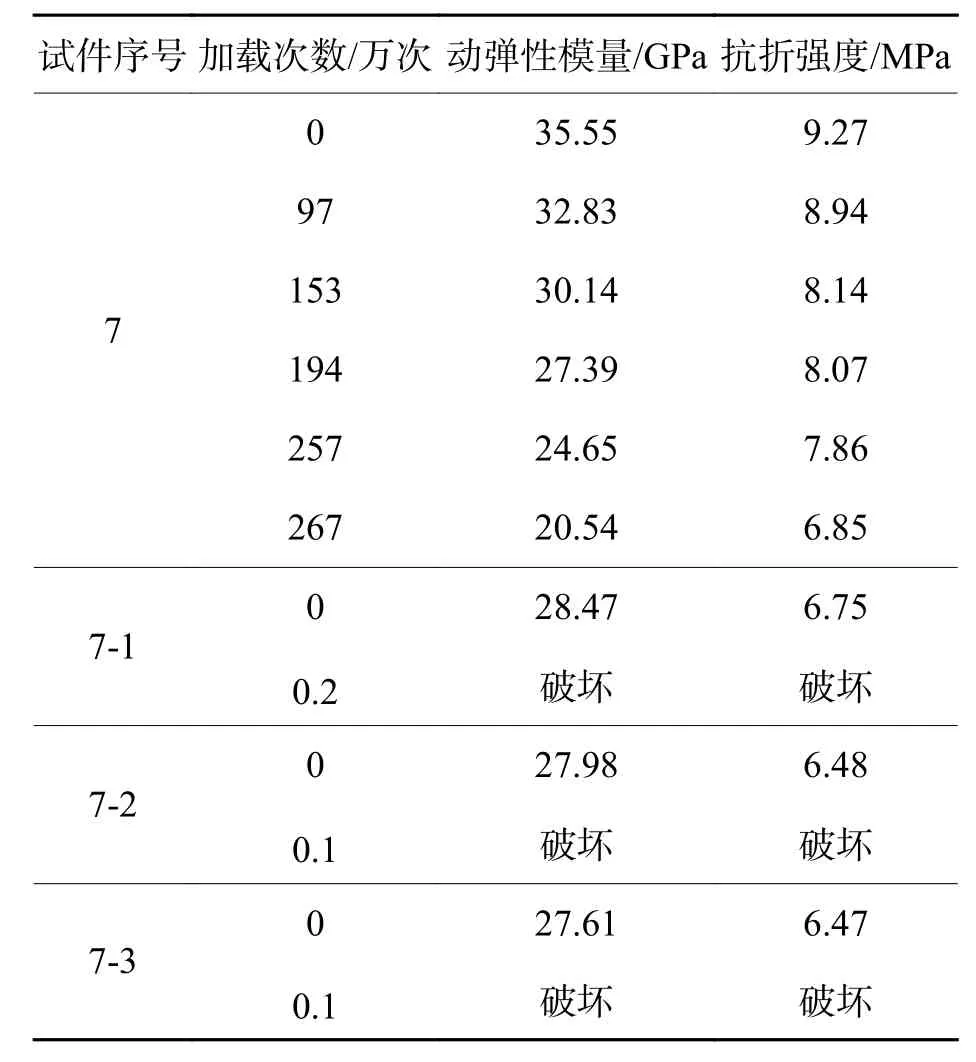
表 6 混凝土力学指标衰变测试结果Tab.6 Mechanics indexes degradation results under the stress level

4.4 不同荷载组合对混凝土力学性能变化规律的影响

根据应力水平和加载频率组合对应的客货车荷载，不同工况对应不同的客货车荷载.其中，应力水平0.3（加载频率10 Hz）和应力水平0.5（加载频率15 Hz）分别代表低速和普速货车荷载工况，应力水平0.3（加载频率15 Hz）和应力水平0.3（加载频率20 Hz）分别代表低速和普速客车荷载工况，应力水平0.7（加载频率15 Hz）代表最不利货车荷载工况.将各种工况的损伤曲线绘在同一坐标系中，如图5所示.

由图5可以看出：在模拟低速和普速货车荷载工况下，混凝土的损伤较模拟低速和普速客车荷载工况下严重；对比低、普速客车的损伤曲线，荷载幅值相同的情况下，在第1阶段，低速客车致损比普速客车致损快，说明低速客车荷载对混凝土初始的损伤发展影响较大；到后期第2、3阶段，两条曲线相互靠近，差别逐渐缩小，说明在损伤发展后期普速客车荷载对混凝土的伤损影响逐步加大.

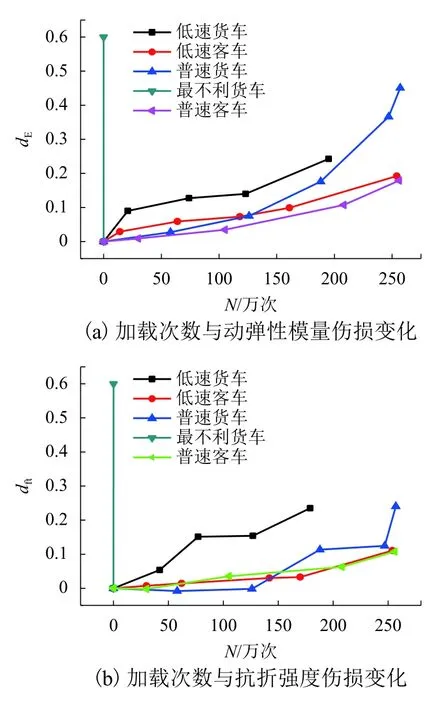
图 5 5种工况下混凝土损伤曲线Fig.5 Degradation curves of concrete mechanical property

结合混凝土动态力学性能的研究现状[28]，普速客车和货车荷载作用使得混凝土轨道板初期的动态抗弯性能有所提高，速度较高且轴重相对较轻的客车荷载使无砟轨道混凝土内部损伤产生和发展的速度相对较慢.随着无砟轨道服役时间增长，混凝土内部损伤开始演化，混凝土极限抗弯能力下降，此时车速对动力系数的影响有所增大，使得无砟轨道线路不平顺的问题加重，车速对动力系数的影响增大，因此普速列车荷载在无砟轨道服役后期会使混凝土动弹性模量及抗折强度损伤的发展加快.

对比低速以及普速货车作用下动弹性模量损伤曲线和抗折强度损伤曲线，第1阶段尽管普速货车的应力水平比低速货车大，但是低速货车荷载的损伤比普速货车荷载作用下轨道板的损伤快，说明低速货车在初期对轨道板损伤影响较大；当无砟轨道损伤累积发展到一定程度时，普速货车荷载作用下轨道板损伤逐渐逼近低速货车荷载作用下轨道板的损伤，最终可能比低速货车荷载作用下轨道板损伤快，线路状态甚至可能使速度较高的货车荷载动力系数大大提高，呈现出最不利货车荷载工况情况，使无砟轨道混凝土在服役过程中出现快速劣化，甚至破坏的情况.

由于在文中测试动弹性模量依照的是现有的弹性波法理论，动弹性模量与波速的关系已经拥有比较成熟完善的理论与实践参考，而测定抗折强度时采用的是波速与力学试验中的抗折强度的拟合标定曲线，有一定的离散性，但是从结果上来看，尽管在局部范围内动弹性模量的损伤程度与抗折强度的损伤程度关联性不明显，从整体趋势上来看，仍然能够在一定程度上说明随着荷载工况的不同，混凝土的力学性能的变化规律，由于是在无砟轨道研究领域内对特定列车荷载下的混凝土的力学性能变化的初探，同时由于试验经费以及试验时间、人员的限制，并没有足够的样本能够精确定量的判断两者的相关性，但是对于定性地推断两者损伤趋势方面能够具有一定的参考意义.

5 结 论

通过试验测试分析混凝土试件在不同应力水平以及频率条件下混凝土材料的动弹性模量和抗折强度力学指标的变化规律，得到以下结论：

（1）在客货车荷载作用下，动弹性模量的损伤程度较抗折强度大.初始混凝土状态在一定范围对其力学性能变化趋势影响不大，受加载的工况影响较大.

（2）在相同的加载频率下，应力水平越大，混凝土动弹性模量以及抗折强度的损伤越严重，应力水平为0.7的工况，混凝土动弹性模量和抗折强度损伤远大于其他工况.说明在货车荷载作用的最不利工况下，轨道板很可能会遭到破坏.

（3）在相同的应力水平下，当加载频率越低，混凝土动弹性模量和抗折强度的衰变越快.在250万次荷载作用后，20 Hz工况下混凝土动弹性模量损伤可能超过15 Hz工况.

（4）对于线路运营初期，低速的客货车荷载都会使混凝土损伤产生的速度更快，当无砟轨道内部已有一定程度的损伤累积，较高速荷载引起的列车荷载动力系数增大问题对混凝土损伤发展的影响较大，此时较高速度的客货车荷载会加速无砟轨道结构损伤的发展.