脉冲风洞测力系统结构动力学特性

吕金洲，张小庆，赵晓男，陈光雄，吴颖川

（1.西南交通大学机械工程学院，四川 成都 610000；2.中国空气动力研究与发展中心高超声速冲压发动机技术重点实验室，四川 绵阳，621000）

脉冲风洞[1-5]是高超声速飞行器技术发展的重要地面试验设备，这类风洞时间很短，启动时冲击载荷很大，引起的模型振动在试验时间内无法衰减，为风洞测力带来很大的困难.

为解决快速测力问题，国内外学者做了大量研究.对于激波风洞，由于试验时间仅为毫秒量级，多采用加速度计天平进行气动力载荷测量，Tanno等[6-7]、 Singh 等[8-9]、 Trivedi等[10]、 Satheesh 等[11]和Saravanan等[12]即通过该方法获得了激波风洞中试验模型的气动力载荷.同样，应力波天平[13]和光学测力技术[14-15]也在激波风洞测力中得到应用.刘洪山等[16]总结了应力波天平在国内激波风洞上的应用.对于试验时间超过100 ms的风洞，则多采用应变天平进行气动力载荷测量，汪运鹏等[17-18]采用应变天平对JF-12激波风洞进行了气动力载荷测量，贺伟等[19]对比脉冲燃烧风洞和长时间风洞测力结果，验证了单分应变天平的脉冲风洞测力方法，王锋等[20]将载荷辨识技术应用于脉冲燃烧风洞模型测力.程忠宇等[21]采用多加速度计振动分离惯性补偿技术对长细比超过20的试验模型进行了测力试验，取得了较为理想的试验结果.

综上所述，加速度计天平主要用于质量较小、试验时间更短的激波风洞，对于试验时间超过100 ms的脉冲风洞，则需采用刚度更高的应变天平，以保证试验过程中模型姿态不发生改变.随着高超声速技术的发展，φ2.4 m脉冲燃烧风洞试验时间超过300 ms，模型长度可达5 m，质量超过1 000 kg，以上特点决定其测力系统需要采用高度较高的应变天平.现阶段天平公式均通过静态校准获得，未考虑振动对测力结果的影响，导致天平输出结果和模型所受到的气动力载荷之间存在误差.为了提高测力精度并进行瞬态测力，需要消除模型振动对测力系统（forcemeasurement system，FMS）输出结果的影响.振动系统为经典二阶系统，外部作用力转化为加速度力、阻尼力和弹性力，天平测量弹性力，跟实际的外部作用力之间差了阻尼力和加速度力.惯性补偿的目的是在弹性力的基础上，叠加加速度力和阻尼力，使其充分逼近外部作用力.因此，本文将惯性补偿方法应用于脉冲风洞试验测力，获得天平弹性输出结果和模型惯性输出结果，两者耦合后消除振动信号，而后计算模型所受到的气动力载荷.

1 测力系统综述

图1为高超声速脉冲风洞试验测力系统简化图，主要包括试验模型、测力天平和支架3部分.试验模型是承受气动力载荷的主要部件，天平为测量设备，支架用于支撑天平和模型，各部分之间通过螺钉连接.

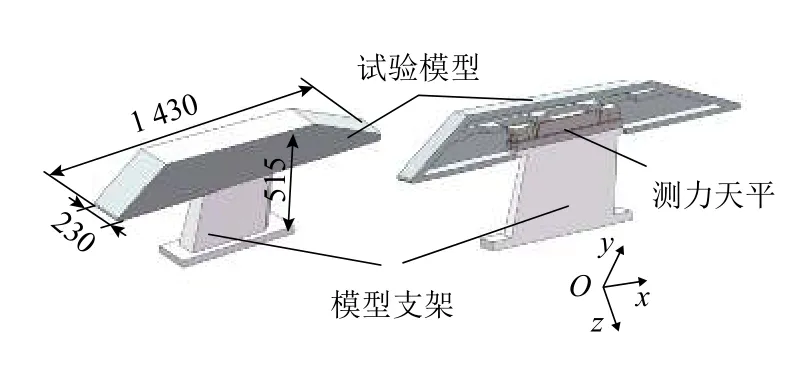
图 1 风洞测力系统Fig.1 Force-measurement system for wind tunnel

图2为3分量测力天平，包括浮动框、固定框和支撑梁3部分，固定框和浮动框通过支撑梁和测量元件连接在一起，该天平具有轴向、法向和俯仰3个分量的刚度，试验过程中测量元件产生应变，导致其上的应变计电阻产生变化，惠斯通电路输出电压，然后根据天平公式计算模型所受到的气动力载荷.

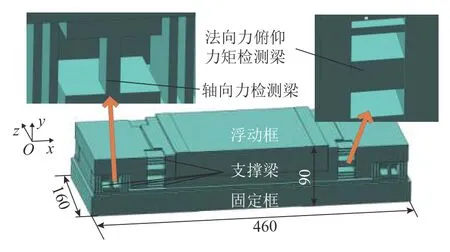
图 2 三分量测力天平Fig.2 3-component force balance

2 测力系统动力学建模

图3（a）为测力系统简化图，试验模型为框架结构，其刚度高于天平，支架为实体金属结构，刚度远大于试验模型和测力天平.因此，将支架及天平浮动框和模型假设为刚体.试验过程中，测力系统的应变最大部位为天平测量元件，将测量元件简化为具有三分量刚度的弹簧，此时测力系统可简化为图3（b）所示梁-弹簧-阻尼系统.其中天平浮动框和模型简化为梁m，弹簧测量元件简化为三分量弹簧k1=(k1x,k1y,k1Mz)和k2= (k2x,k2y,k2Mz)，由天平的对称性，k1x、k1y、k1Mz分别等于k2x、k2y、k2Mz.测力系统的阻尼简化为c1和c2.

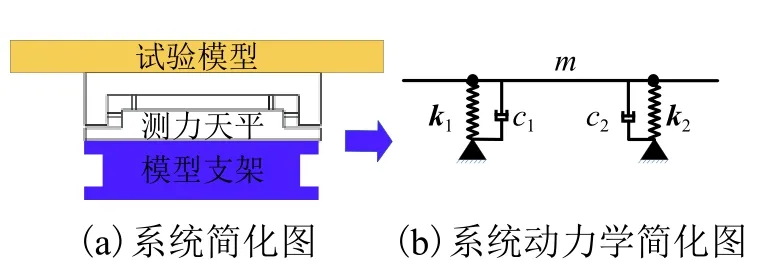
图 3 测力系统Fig.3 Force measuring system

根据以上简化结果可得到测力系统的动力学方程，如式（1）所示.

式中：M、C和K分别为系统质量、阻尼和刚度矩阵；q和F分别为模型位移和气动力载荷向量.

当K和C足够小时，天平可视为完全自由系统，在这种条件下，测力系统为惯性系统，因此仅需要知道模型的质量和转动惯量即可描述其响应特性，该条件即为加速度计天平的工作原理.当K和C无法忽略时，该测力系统称为刚度系统，φ2.4 m脉冲燃烧风洞试验测力系统即属于该类型，振动特性由M、C和K决定.如式（1）所示，测力系统所受到的气动力载荷等于弹性、阻尼和惯性输出结果之和，但是阻尼载荷很小，分析时进行了忽略.惯性补偿方法即将测力天平输出的结果在时域范围内与试验模型输出的惯性载荷进行耦合，消除振动对测量的干扰，获得测力系统的输出.

3 测力系统分析

3.1 虚拟标定

为计算测力系统弹性输出结果，首先需要对其进行虚拟标定，获得系统刚度矩阵K.图4为天平应变计粘贴位置（括号内编号为相应位置的对侧），为提高惠斯通电路输出电压，应变计应尽可能靠近测量元件的根部.11～18为轴向力测点，输出y向应变，结果记为μ11～μ18；21～28 和 61～68 分别为法向力和俯仰力矩测点，输出x向应变，结果记为μ21～μ28和μ61～μ68.

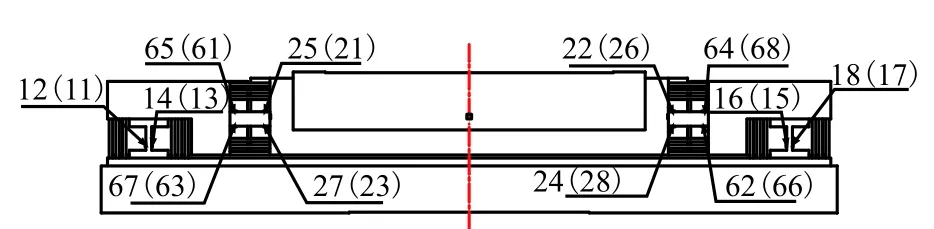
图 4 天平应变计粘贴位置Fig.4 Strain gauge positions on force balance

测力系统静态标定公式为

式中：

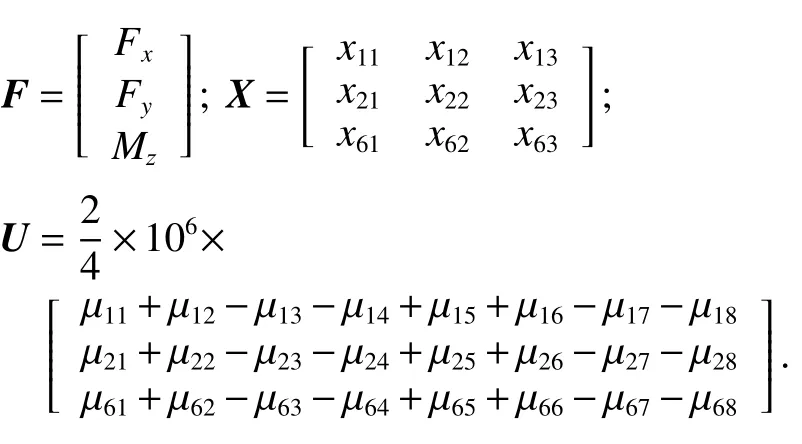
在向量F中，Fx、Fy和Mz分别为标定时对模型施加的轴向力、法向力和俯仰力矩.系数矩阵X中，x11、x22、和x63为主系数，x12、x13、x21、x23、x61、和x62为干扰系数.通过矩阵变换，测力系统刚度系数矩阵：

为计算X，需要对测力系统施加3个不相关的载荷向量，获得测点的应变值，将结果代入式（3）进行求解.

图5（a1）和（b1）分别为测力系统网格加密前、后的有限元模型，加密前测力系统包含137 883个节点和23 192个单元，加密后其节点数为58.2万，网格数量为12.41万，两者均大幅度提高，以上各分部件均采用六面体网格划分.对于测力天平，其测量元件和支撑梁等部位进行了加密，以便准确获得测点应变，浮动框和固定框等应变较小的部位则较为稀疏.试验模型和支架材料为45钢，密度7 850 kg/m3，弹性模量为200 GPa，泊松比为0.3；天平材料为Ni18Co8 Mo5TiAl，密度为 8 000 kg/m3，弹性模量为187.25 GPa，泊松比为 0.27.加载位置如图 5（a1）、（b1）所示.边界条件为支架底面固定，施加的3个载荷分别为F1= （1 000，0，0）T，F2= （0，5 000，0）T，F3=（0，0，1 000）T，其中，第 1、2项单位为 N，第 3项单位为 N·m.

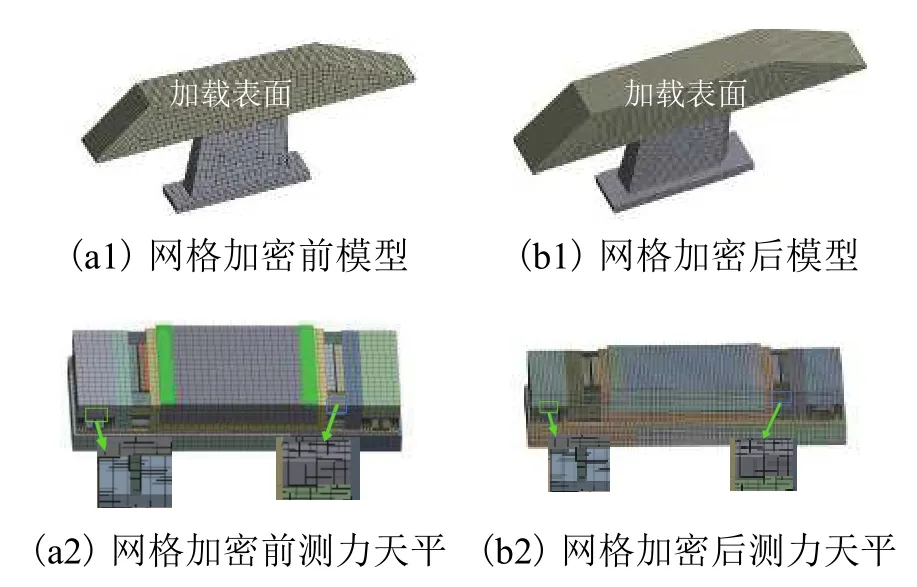
图 5 测力系统有限元模型Fig.5 Finite element model of FMS

根据仿真结果和式（3）解得测力系统有限元模型加密前后的弹性系数矩阵分别为

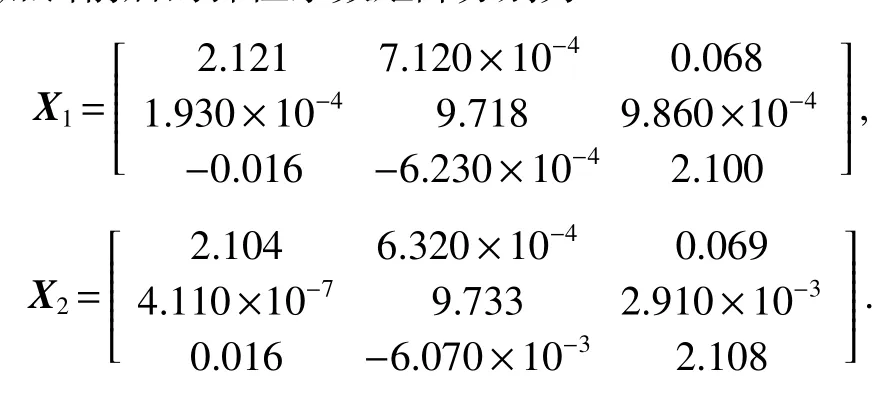
X1和X2显示，除主系数外，x13和x61远大于其它的干扰系数，这说明对于该测力系统，轴向力和俯仰力矩之间的耦合较为强烈，其它的干扰系数x12、x21、x23和x62相对很小，说明轴向力和法向力或俯仰力矩之间的耦合较弱.对比X1和X2可知，两者主系数相差很小，这说明对测力系统有限元模型网格大幅加密后，计算所获得的刚度矩阵变化很小，从而说明图5（a1）所示有限元模型足够精确，能够满足研究的需要.

3.2 输入载荷的确定

图6为φ2.4 m脉冲燃烧风洞试验段总压和各分量载荷输出结果变化规律（t为时间）.如图6所示，风洞启动后，试验段总压不断升高，而后达到稳定，持续约400 ms，燃料喷注时间约在风洞启动后50 ms.各分量输出结果均近似正弦规律变化，因此，确定输入载荷形式为正弦与阶跃的叠加形式.

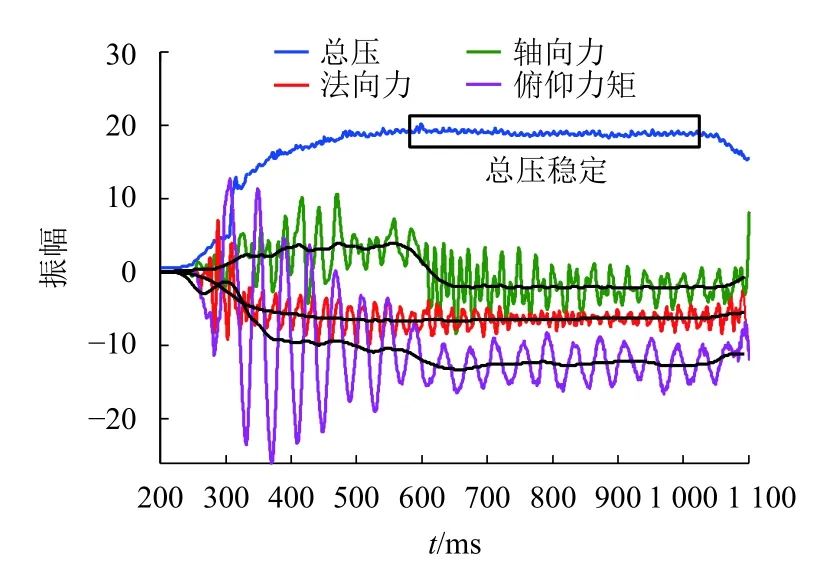
图 6 试验段总压及天平测量结果Fig.6 Total pressure of test chamber and measurement results of force balance

由于试验过程中模型所受气动力载荷无法确定，无法获得试验过程中风洞气流的波动频率，因此在对测力系统进行加载时，输入载荷的正弦部分频率分别为固有频率的0.5倍 （half times of the natural frequency，记为 H-f）、1 倍 （natural frequency，记为N-f）和 2 倍 （double times of the natural frequency，记为D-f），研究输入载荷频率低于、等于和高于系统固有频率时的瞬态响应.

为确定测力系统的固有频率，需要对其进行模态分析，结果如图7和表1所示，其轴向、法向和俯仰方向振动模态分别为三阶、六阶和一阶，相应的固有频率分别为121、172.64 Hz和80.65 Hz，仿真时均进行3分量加载.

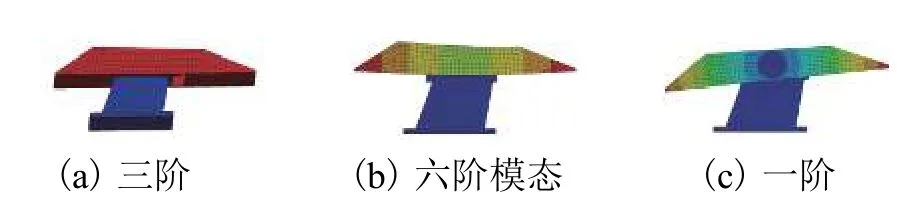
图 7 测量系统振型Fig.7 Vibration modes of FMS

表 1 测力系统模态参数Tab.1 Mode parameters of FMS

3.3 惯性载荷的获取

测力系统振动时必然存在弹性变形，要准确获得其惯性输出载荷十分困难，但模态分析结果表明，测力系统轴向振动以试验模型、天平浮动框和浮动框与固定框连接件的整体振动为主，法向和俯仰方向振动均以天平浮动框和试验模型整体振动为主，因此，可假定各分量振动为不同部件的整体振动.根据测力系统不同模态下振动部分的不同，通过3D软件获得测力系统的质量矩阵M（忽略质量矩阵中的干扰项）为

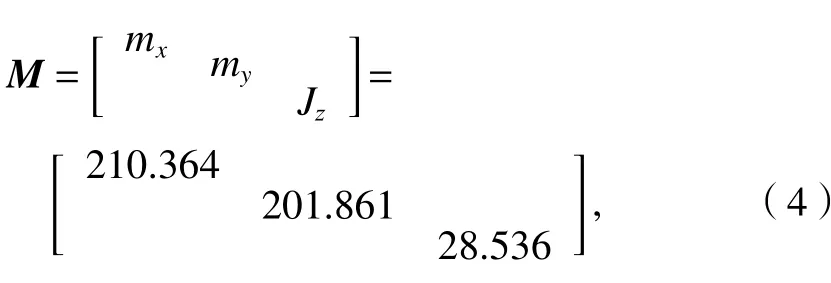
式中：mx和my分别为测力系统轴向和法向振动质量；Jz为其绕z轴的转动惯量.

为获得测力系统振动时输出的惯性载荷，分析时提取了多点的加速度，图8为加速度测点的位置.

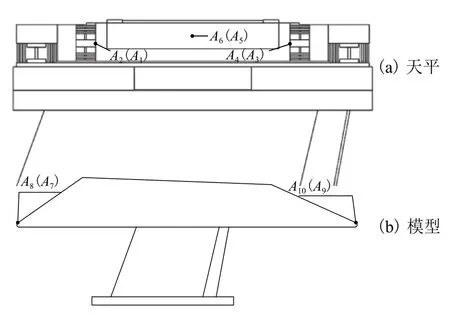
图 8 测力系统加速度测点Fig.8 Acceleration detection points of FMS

图 8中：A1～A6位于天平上，A7～A10位于模型上，其中取A1～A6点的x向的加速度均值作为测力系统x向的加速度，A1～A10点的y向的加速度均值作为测力系统y向的加速度，通过组合A7～A10加速度的变化结果获得测力系统的绕z轴转动的角加速度，测力系统加速度a具体算法如式（5）.

根据牛顿第二定律得测力系统惯性载荷为

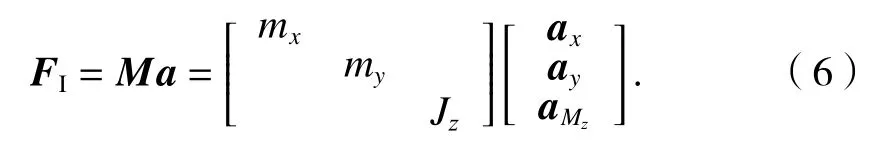
3.4 瞬态仿真结果

3.4.1 H-f正弦阶跃载荷加载

图9为H-f 正弦阶跃载荷加载时测力系统的仿真结果.其中，图 9（a）为输入载荷，图 9（b）为弹性输出载荷，图 9（c）为惯性输出载荷，图9（d）为弹性输出载荷和惯性输出载荷叠加后的结果.

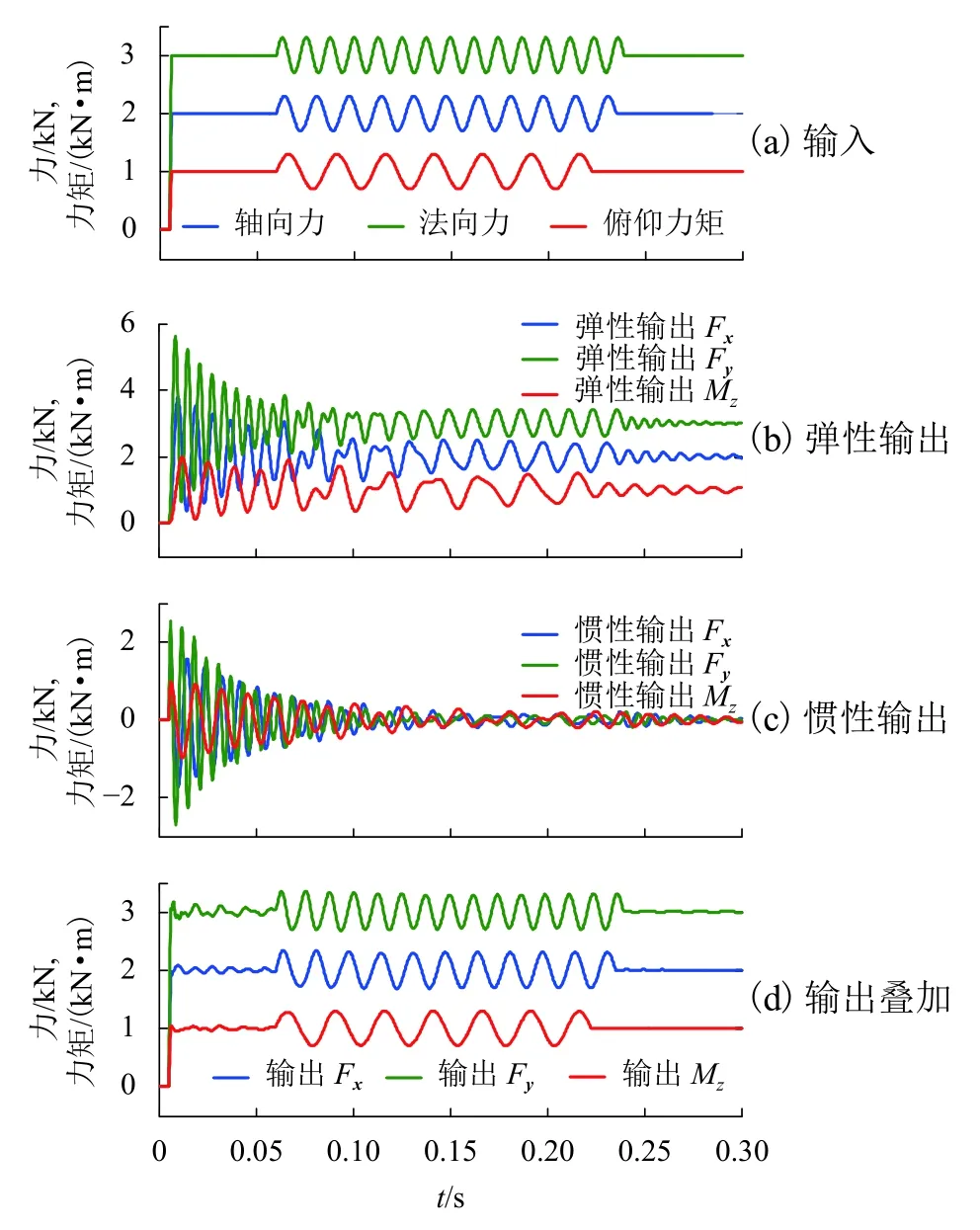
图 9 H-f正弦阶跃载荷加载时测力系统仿真结果Fig.9 Simulation results of FMS under action of H-f sine step load

从图9（a）中可以看出，轴向力、法向力和俯仰力矩从0增加到2、3 kN和1 kN·m，持续一段时间后，按照正弦规律进行振动，其振幅为300 N或N·m，3分量载荷的频率分别为60、81 Hz和40 Hz （即为相应固有频率的一半），振动一段时间后，输入载荷恢复稳定状态.

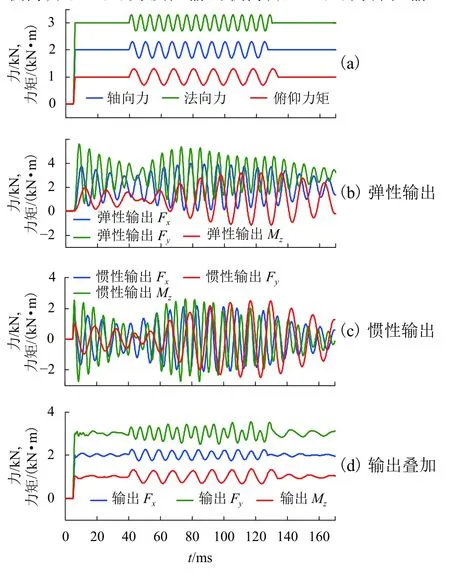
图 10 N-f正弦阶跃载荷加载时测力系统仿真结果Fig.10 Simulation results of FMS under action of N-f sine step load

测力系统仿真结果显示，惯性补偿前轴向力、法向力和俯仰力矩的幅值分别为3 795.5、5 620.6 N和1 982.1 N·m，惯性补偿后三者的幅值分别为2 344.9、3 364.2 N和1 305.0 N·m，补偿后幅值明显减小，接近于输入幅值.

分析结果显示，阶跃载荷加载阶段，测力系统自由振动被激发，而后逐渐衰减.正弦加载阶段，振动转变为自由振动和输入载荷的耦合振动.惯性补偿后，测力系统输出结果不仅振幅大幅度减小，而且瞬态输入输出基本一致.

3.4.2 N-f正弦阶跃载荷加载

图10为N-f 正弦阶跃载荷加载时测力系统输出结果.图 10（a）为输入载荷，图 10（b）为弹性输出载荷，图 10（c）为惯性输出载荷，图 10（d）为弹性输出载荷和惯性输出载荷叠加结果.输入载荷形式与H-f 加载时近似，不同之处在于正弦阶段3分量频率分别为120、172 Hz和80 Hz，即为相应的固有频率.计算时对有限元模型施加瑞利阻尼，以保证测力系统振幅不会发散.

测力系统仿真结果表明，惯性补偿前弹性输出结果幅值分别为3 985.2、5 605.4 N和3 161.8 N·m，惯性补偿后分别为2 257.3、3 538.4 N和1 320.2 N·m，补偿后明显减小，接近于输入值.

从图10中可以看出，当N-f 正弦阶跃载荷施加于测力系统时，系统产生共振，共振对弹性和惯性输出载荷均产生很大影响，表现为正弦加载阶段弹性和惯性输出均大幅增加.弹性瞬态载荷大幅超出输入载荷，测量元件的变形可能超过其弹性极限，造成天平损坏.共振同时放大了不同分量间的耦合关系，导致惯性补偿后，输入输出结果之间仍然存在较大的误差，轴向力输出结果尤为明显.

3.4.3 D-f 正弦阶跃载荷加载

图11为D-f 正弦阶跃载荷加载时测力系统的输出结果.图 11（a）为输入载荷，图 11（b）为弹性输出结果，图 11（c）为惯性输出结果，图 11（d）为弹性输出载荷和惯性输出结果叠加后测力系统的输出.输入载荷形式与H-f 和N-f 正弦阶跃载荷近似，不同之处在于正弦加载部分的频率分别为240、344 Hz和160 Hz，为相应固有频率的2倍.

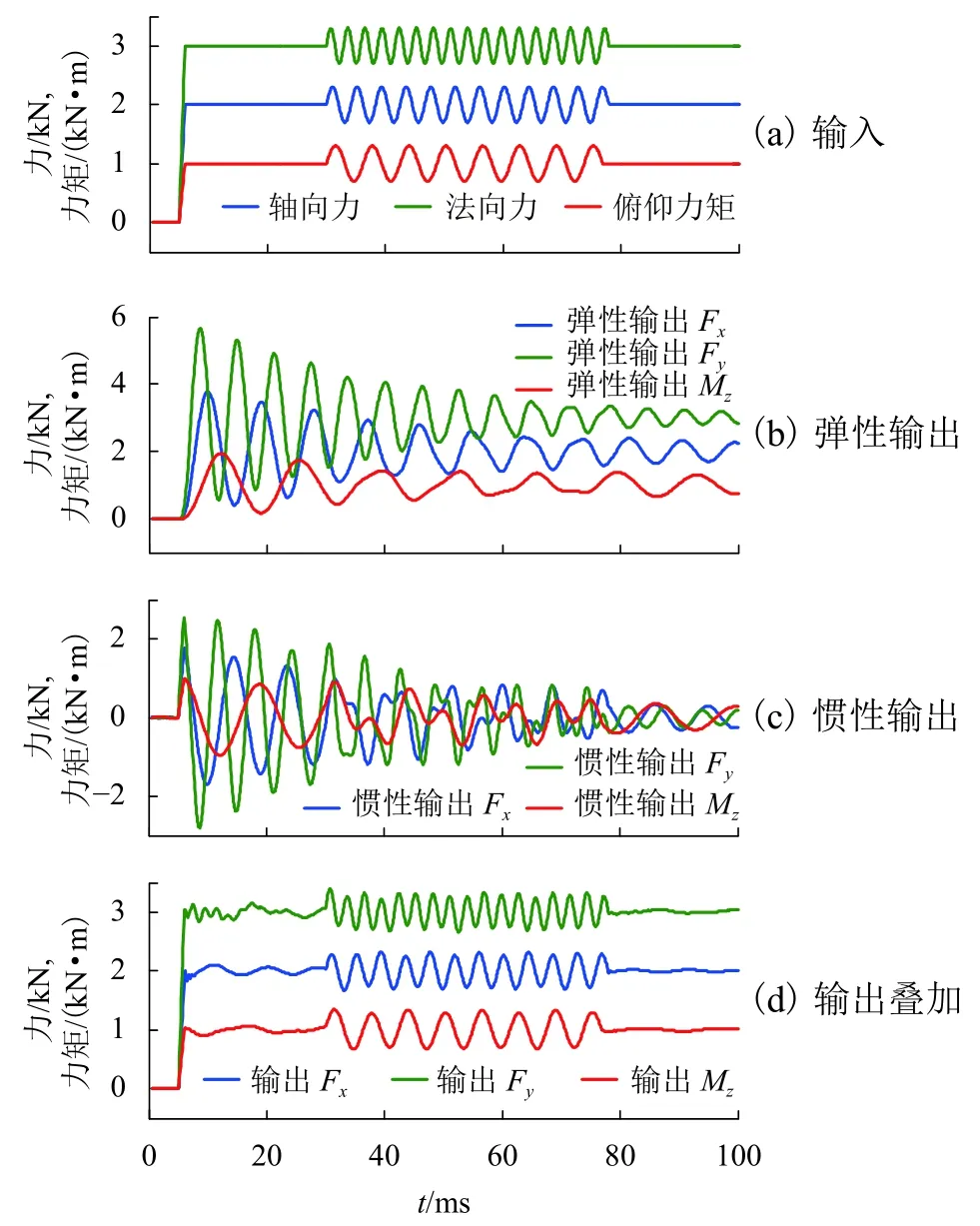
图 11 D-f正弦阶跃载荷加载时测力系统仿真结果Fig.11 Simulation results of FMS under action of D-f sine step load

输出结果表明，惯性补偿前各分量幅值分别为3 777.6、5 656.0 N 和 1 948.2 N·m，惯性补偿后分别为 2 330.3、3 395.6 N和 1 346.1 N·m，幅值明显减小，且接近于输入幅值.

分析结果表明，当N-f 正弦阶跃载荷施加于测力系统时，阶跃载荷加载阶段其自由振动被激发，此时输出结果最大，该阶段输出结果频率为测力系统的固有频率；正弦加载阶段系统转变为强迫振动，主要为加载形式和自由振动形式的耦合.惯性补偿后测力系统幅值大幅减小，而且输入输出结果基本一致.

3.5 测量精度分析

对于仿真分析结果定义加载时间段内输出结果与输入载荷之间的差值为测量误差D，如式（7）所示.

式中：FO为测力系统输出结果；FI为测力系统输入载荷.

测量结果的误差率定义为

式中：A为输入载荷的基准值或幅值.

3.5.1 均值测量精度分析

表2为测力系统各分量均值测量精度，从表中可以看出，当输入载荷频率为H-f 和N-f 时，均值测量精度高于99%，惯性补偿后略有提高，当输入载荷的频率为D-f 时，均值测量精度高于98.5%，惯性补偿后误差低于原来的1/2.分析结果表明，惯性补偿前后均值输出误差均很小，说明无论是否进行惯性补偿，均可以天平输出结果均值作为模型受到的静态气动力载荷.

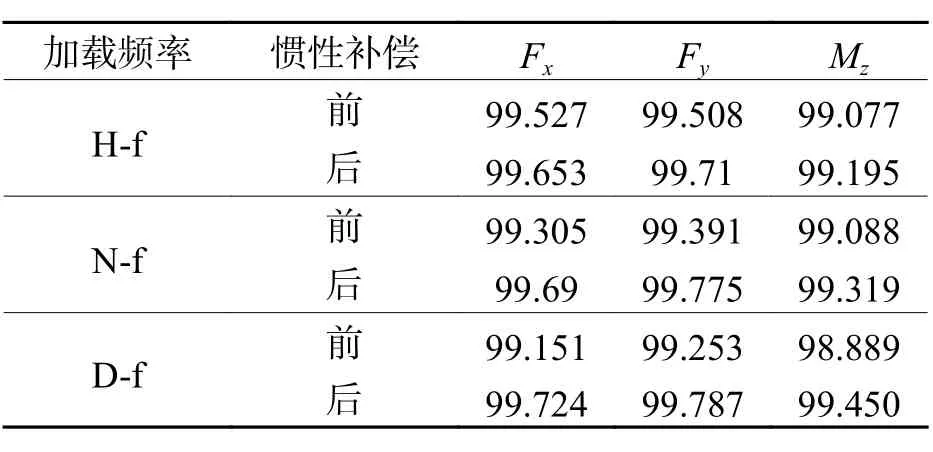
表 2 测力系统各分量均值测量精度Tab.2 Mean measurement accuracy of FMS in each component %

3.5.2 瞬态测量精度分析

图12和图13分别为测力系统惯性补偿前、后测力系统不同加载时的瞬态测量误差（由式（7）计算所得），该结果仅反应了加载时间内的测量误差，其中图 12（a）、（b）、（c）和图 13（a）、（b）、（c）分别为正弦加载频率为H-f、N-f 和D-f 时的测量误差.当加载频率为H-f 时，惯性补偿前轴向力、法向力和俯仰力矩的误差范围分别为-1 744～1 850.1、-2 562.2～2 568.8 N和-912～969.9 N·m，惯性补偿后分别为-56.8～77.3、-130.8～176.7 N 和-48.4～43.6 N·m；当加载频率为N-f 时，惯性补偿前轴向力、法向力和俯仰力矩的误差范围分别为-2 205.4～2 201.5、-2 590.6～2 567.1 N 和-2 406.9～2 395.2 N·m，惯性补偿后分别为-134.3～114.5、-236.7～249.7 N 和-126.4～121.1 N·m；当加载频率为D-f时，惯性补偿前轴向力、法向力和俯仰力矩的误差范围分别为-1 758.9～1 849.3、-2 637.1～2 565.4 N 和-909～969.7 N·m，惯性补偿后分别为-99.6～99.9、-154.1～146.6 N和-95.1～63.8 N·m.对比以上结果可以发现，惯性补偿后输出结果误差的幅值大幅度下降，较为接近测力系统的输入载荷.

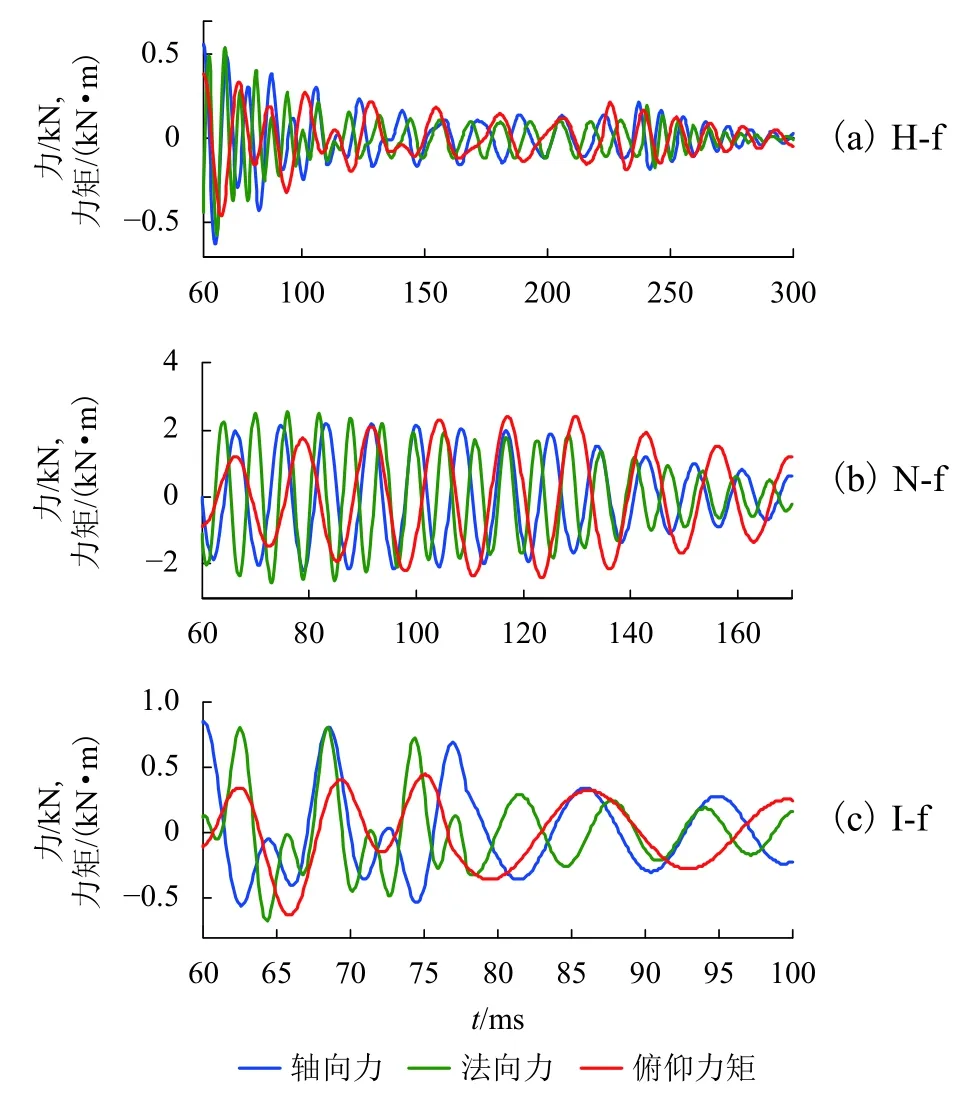
图 12 测力系统惯性补偿前输出结果误差Fig.12 Transient measurement errors of FMS before inertia compensation

表3为测力系统不同加载条件下的测量精度最小值.当加载频率为H-f时，瞬态测量精度高于93%；当加载频率为N-f时，瞬态测量精度高于87%；当加载频率为D-f时，瞬态测量精度高于92%.从表3中可以看出，瞬态测量精度普遍高于91%，仅共振条件下约为87%，说明惯性补偿后测力系统的输出结果在一定范围内可作为其受到的瞬态气动力载荷.同时系统产生共振时，各分量输出结果的瞬时测量精度均低于其他状态，说明共振不仅容易造成天平的损坏，而且会降低测力系统的测量精度.

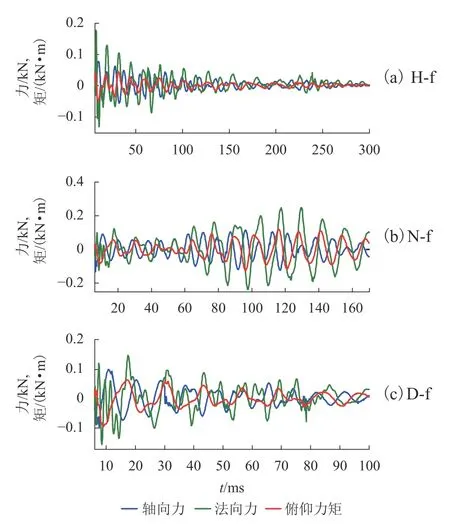
图 13 测力系统惯性补偿后输出结果误差Fig.13 Transient measurement errors of FMS after inertia compensation

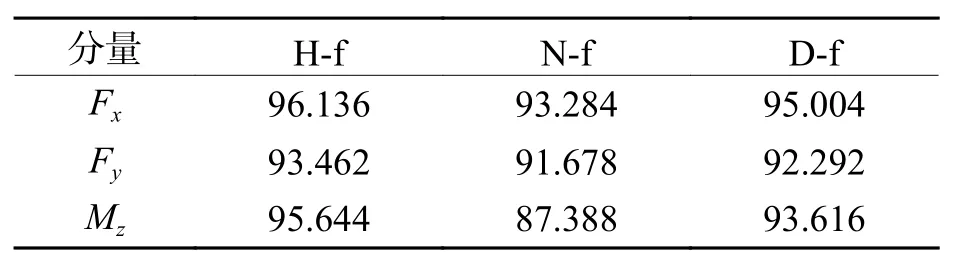
表 3 测力系统瞬态测量精度最小值Tab.3 Minimum values in measurement accuracy of FMS %

4 试验结果

测力系统风洞试验在φ2.4 m脉冲燃烧风洞中开展，测力系统安装于风洞试验段中，试验马赫数为6.5，在该状态下，风洞总压为6.54 MPa，总温约为1 676 K，总焓为2.145 9 MJ/kg.从风洞喷管中射出的气流，O2、H2O和N2的摩尔组分比例分别为0.207 1、0.232 6和0.560 3，平均摩尔分子量为26.5 g/mol.试验过程中风洞的静温为210.5 K，静压为51.3 kPa，比热比为1.281 5，试验过程中模型攻角为0°.

测力系统的弹性输出结果可根据天平公式计算获得，此次试验的天平公式如式（9）.

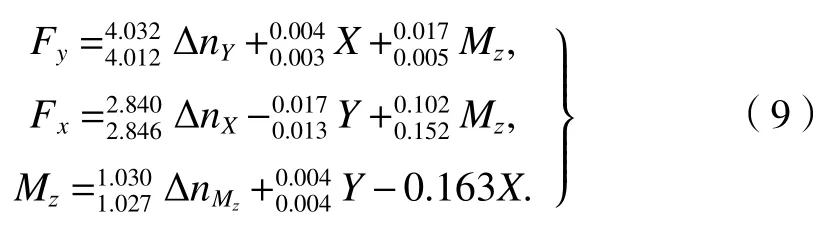
加速度计位置如图14中的A1和A2，两者之间的轴向距离为600 mm，均为3 向加速度传感器，分别记测点A1和A2的x向的加速度为a1x和a2x，y向的加速分别为a1y和a2y，根据测点A1和A2的x、y向的加速度计算试验过程中模型振动的加速度，结果如式（10）所述.

图 14 风洞试验测力系统Fig.14 FMS in wind tunnel

通过测量获得测力系统的质量矩阵如下：

而后根据式（6）计算测力系统的质量惯性输出结果.

图15为根据式（9）和式（6）计算所得的测力系统弹性输出结果和惯性输出结果，以及惯性补偿后测力系统的输出结果.从图中可以看出，惯性补偿前的轴向力Fx、法向力Fy和俯仰力矩Mz的波动范围分别为-1 333.8～2 650.1、-1 288.4～2 912.6 N和-2 203.8～457.8 N·m，惯性补偿后，三者的波动范围分别为-4.8～2 102.2、-13.13～1 896.1 N 和-1 074.6～2.5 N·m.惯性补偿后测力系统的各分量输出结果曲线的变化规律均与风洞后室总压的变化一致，证明惯性补偿后测力系统的输出结果可以作为试验模型在风洞气流中受到的气动力载荷.

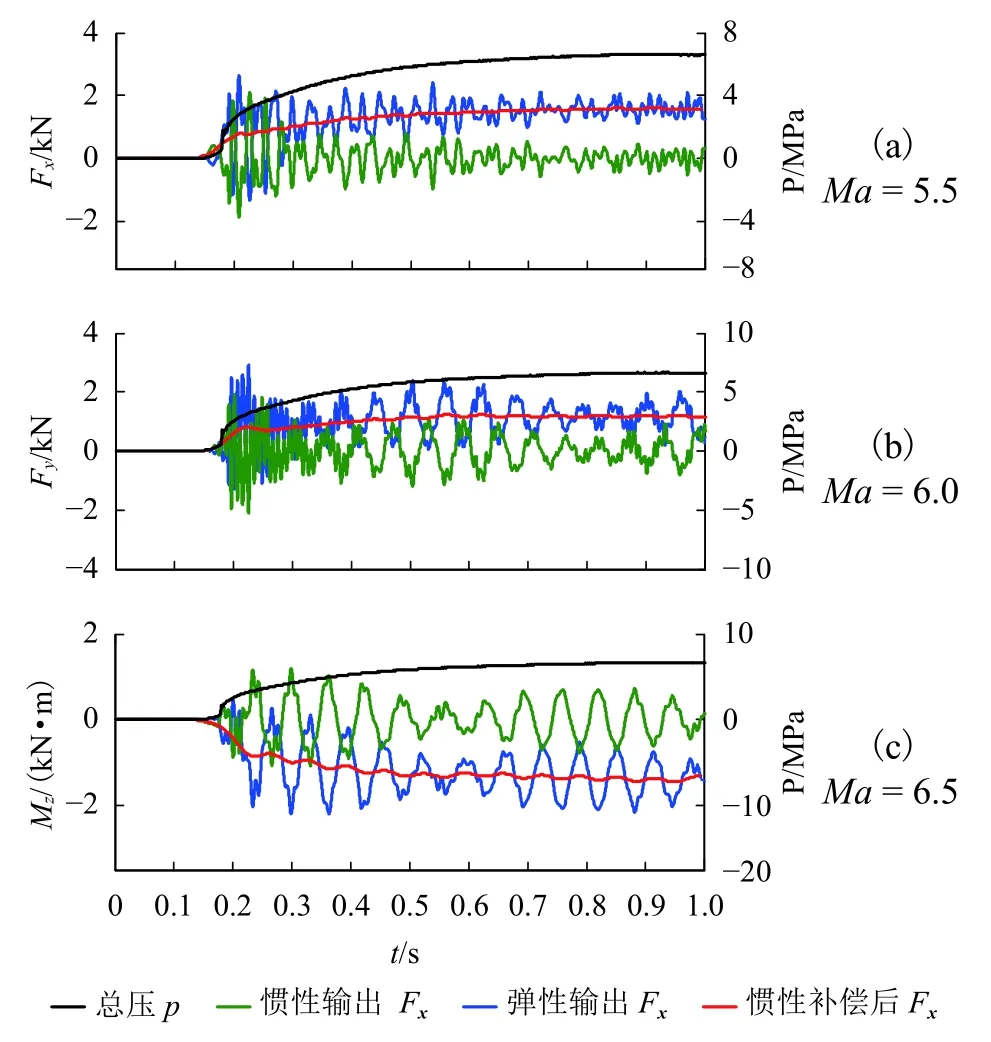
图 15 风洞试验结果Fig.15 Wind tunnel test results

5 结 论

本文基于惯性补偿方法对高超声速测力系统进行了研究，包括理论建模、静态虚拟标定、模态分析、瞬态分析和惯性补偿，得到以下结论：

（1）分析可知惯性补偿前测力系统均值测量精度高于98.9%，弹性输出均值可作为测力系统所受到的静态气动力载荷，对结果进行惯性补偿可进一步提高测量精度，惯性补偿后测量精度高于99.2%；

（2）测力系统产生共振时，惯性补偿前瞬时输出结果幅值大大超出输入载荷幅值（超出量分别为：985、1 605 N和 1 162 N·m）不仅容易造成天平损坏，还会对瞬态测量结果产生干扰；

（3）在一定精度范围内，当输入载荷频率远离测力系统固有频率时，可以将惯性补偿后的输出结果作为试验模型受到的瞬态气动力载荷.

参考文献：

[1]STALKER R J.A study of the free-piston shock tunnel[J].AIAA Journal， 1967， 5(12)： 2160-2165.

[2]PATE S R， SILM L G， STALLINGS D W， et al.Development of an MHD-augmented， high enthalpy，shock tunnel facility[J].AIAA Journal，1974，12(3)：289-297.

[3]OLIVIER H， GROENIG H， BOZEC A L.Hypersonic

model testing in a shock tunnel[J].AIAA Journal，1995， 33(2)： 262-265.

[4]ROBINSON M J， MEE D J， TSAI C Y， et al.Threecomponent force measurements on a large scramjet in a shock tunnel[J].Journal of Spacecraft & Rockets，2004， 41(3)： 416-425.

[5]SCHULTZ I A， GOLDENSTEIN C S， STRAND C L， et al.Hypersonic scramjet testing via diode laser absorption in a reflected shock tunnel[J].Journal of Propulsion & Power， 2014， 30(6)： 1586-1594.

[6]TANNO H，KOMURO T，SATO K，et al.Aerodynamic force measurement technique with accelerometers in the impulsive facility HIEST[M]//Shock Waves.Berlin： Springer， 2009： 471-476.

[7]TANNO H， KOMURO T， TAKAHASHI M， et al.Unsteady force measurement technique in shock tubes[J].Review of Sci-entific Instruments，2004，75(2)： 532-536.

[8]SINGH P， MENEZES V， IRIMPAN K J， et al.Impulse force bal-ance for ultrashort duration hypersonic test facili-ties[DB/OL].（2015-5-24）[2017-08-18]. https://www.hindawi.com/journals/sv/2015/803253/.

[9]SINGH P， TRIVEDI S， MENEZES V， et al.D ynamic calibration and validation of an accelerometer force balance for hypersonic lifting models[J].The Scientific World Journal， 2014， 2014(6)： 813759.

[10]TRIVEDI S，MENEZES V.Measurement of yaw，pitch and ide-force on a lifting model in a hypersonic shock tunnel[J].Measurement，2012，45(7)： 1755-1764.

[11]SATHEESH K， JAGADEESH G.Analysis of an internally mount-able accelerometer balance system for use with non-isotropic models in shock tunnels[J].Measurement， 2009， 42(6)： 856-862.

[12]SARAVANAN S， JAGADEESH G， REDDY K P J.Aerodynamic force measurement using 3-component accelerometer force balance system in a hypersonic shock tunnel[J].Shock Waves， 2009， 18(6)： 425-435.

[13]SMITH A L，MEE D J，DANIEL W J T，et al.Design，modelling and analysis of a six component force balance for hypervelocity wind tunnel testing[J].Computers & Structures， 2001， 79(11)： 1077-1088.

[14]LAURENCE S J， HORNUNG H G.Image-based force and mo-ment measurement in hypersonic facilities[J].Experiments in Fluids， 2009， 46(2)： 343-353.

[15]LAURENCE S J，KARL S.An improved visualization-based force-measurement technique for short-duration hypersonic facilities[J].Experiments in Fluids， 2010， 48(6)： 949-965.

[16]刘洪山，徐翔，姜华.应力波天平在国内激波风洞上的应用[J].实验流体力学，2006，20(1)： 36-39.LIU Hongshan， XU Xiang， JIANG Hua， et al.The application of the stress wave force balance in shock tunnel[J].Journal of Experiments in Fluid Mechanics，2006， 20(1)： 36-39.

[17]WANG Yunpeng， LIU Y， LUO C， et al.Force measurement using strain-gauge balance in a shock tunnel with long test duration[J].Review of Scientific Instruments， 2016， 87(5)： 1068.

[18]WANG Y， LIU Y， JIANG Z.Design of a pulse-type strain gauge balance for a long-test-duration hypersonic shock tunnel[J].Shock Waves， 2016， 26(6)： 1-10.

[19]贺伟，童泽润，李宏斌.单模块超燃发动机推力测量天平研制[J].航空动力学报，2006，20(1)： 36-39.HE Wei， TONG Zerun， LI Hongbin.Investigation of thrust balance for the single module scramjet[J].Journal of Aerospace Power， 2006， 20(1)： 36-39.

[20]王锋，贺伟，毛鹏飞，等.脉冲风洞测力系统建模与载荷辨识方法研究[J].振动与冲击，2015，34(1)： 94-103.WANG Feng， HE Wei， MAO Pengfei， et al.D ynamic modeling of testing system in impulse facilities and load identification method[J].Journal of Vibration and Shock， 2015， 34(1)： 94-103.

[21]程忠宇，陈宏，张琦.多加速度计振动分离惯性补偿测力技术[J].流体力学实验与测量，1999，13(4)： 57-61.CHENG Zhongyu， CHEN Hong， ZHANG Qi.Inertia compensation technology based on multi-accelerometer vibration separating[J].Experiments and Measurements in Fluid Mechanics， 1999， 13(4)： 57-61.