浮置板下声子晶体隔振器带隙特性研究

农兴中，李 祥，刘堂辉，盛 曦，王 平，赵才友

（1.广州地铁设计研究院股份有限公司， 广东 广州 510010；2.西南交通大学高速铁路线路工程教育部重点实验室，四川 成都 610031；3.西南交通大学土木工程学院，四川 成都 610031）

随着我国地铁的大规模修建，地铁运行引起的环境振动越来越影响人们的生产与生活[1]，地铁诱发的地面建筑振动频率成分主要为80 Hz以下的低频振动[2]，而人体对低频振动较为敏感[3-4]，因此地铁减振措施主要针对于低频振动.浮置板道床作为地铁常用减振措施，通过道床减振的方式隔离向环境土壤传播的垂向振动.浮置板轨道系统实现隔振的原理是在轨道与基础之间插入一个固有频率极低的质量-弹簧系统，由浮置板道床提供较大质量，由浮置板板下支承提供较低的垂向刚度，可衰减频率范围在倍固有频率以上的振动成分[5].常用的浮置板板下支承类型有钢弹簧与橡胶隔振器.

目前声子晶体在减振降噪领域的研究成果丰富，1993年，Kushwaha[6]在研究镍/铝二维固体周期复合介质时首次提出了声子晶体的概念；Koo等[7]将声子晶体引入管路系统中，将管路加周期弹性支撑，得到了弯曲振动带隙并进行实验验证，发现其带隙对弯曲振动有一定隔振效果；Sheng等[8]提出了声子晶体的局域共振带隙机理，这标志着声子晶体研究的重大突破；Yu等[9]率先将声子晶体理论引入到梁板类结构设计中，实现了利用带隙特性抑制一定频率范围内的振动传播.本文作者所在课题组已将声子晶体理论初步应用于轨道结构研究中，其中文献[10]基于声子晶体理论提出了一种用于浮置板下满铺支承的减振垫板，进行了一定的理论计算与带隙优化工作，但是未考虑减振垫对整体轨道减振效果的影响，且制造精度和难度较高.因此，本文对文献[10]中提出的元胞结构进行优化，将满铺的减振垫改为点支撑的隔振器，通过结构设计使其垂向刚度与传统钢弹簧一致，建立了三维声子晶体隔振器浮置板轨道有限元模型，计算了整体结构的力传递率，并与传统钢弹簧浮置板轨道的计算结果进行对比.此外，计算了声子晶体隔振器的垂向刚度.

1 声子晶体隔振器简介

声子晶体是由两种或两种以上弹性介质组成的具有弹性波带隙的周期复合材料.弹性波在声子晶体中传播时，受其内部周期结构的作用，形成特殊的色散关系，将没有色散关系曲线的频率范围称为带隙.理论上，带隙频率范围的弹性波传播被抑制，而其它频率范围（称为通带）的弹性波将在色散关系的作用下无损耗地传播.声子晶体的带隙机理有两种，分别为布拉格散射机理与基于共振机理，本文的声子晶体隔振器基于声子晶体局域共振机理，与传统钢弹簧的安装位置一致，声子晶体橡胶隔振器浮置板轨道结构示意图如图1所示.

图 1 声子晶体隔振器浮置板轨道结构示意Fig.1 Schematic diagram of the floating slab track with vibration isolators of phononic crystals

本文所设计的声子晶体隔振器一维声子晶体结构元胞由橡胶垫层、钢散射体、软橡胶材料和基体外壳（铝合金）组成，如图2（a）所示，声子晶体隔振器由3个元胞构成.软橡胶和钢散射体形成局域振子，提供局域共振型带隙，而基体外壳和橡胶垫层主要提供垂向刚度.声子晶体隔振器元胞几何尺寸如图2（b）所示，上图为声子晶体元胞俯视图的一半，下图为声子晶体元胞的前视剖面图，几何材料参数如表1所示.

声子晶体隔振器尺寸与钢弹簧隔振器相差不大，可匹配现有浮置板钢弹簧隔振器的空间设计，将其置于浮置板与基底之间.声子晶体隔振器作为功能部件，可产生低频宽带的带隙，抑制带隙频率范围内的弹性波从浮置板道床向基底的传播；作为结构部件，可为浮置板提供垂向刚度，形成固有频率较低的质量-弹簧系统[11]，保留传统浮置板道床的减振效果.

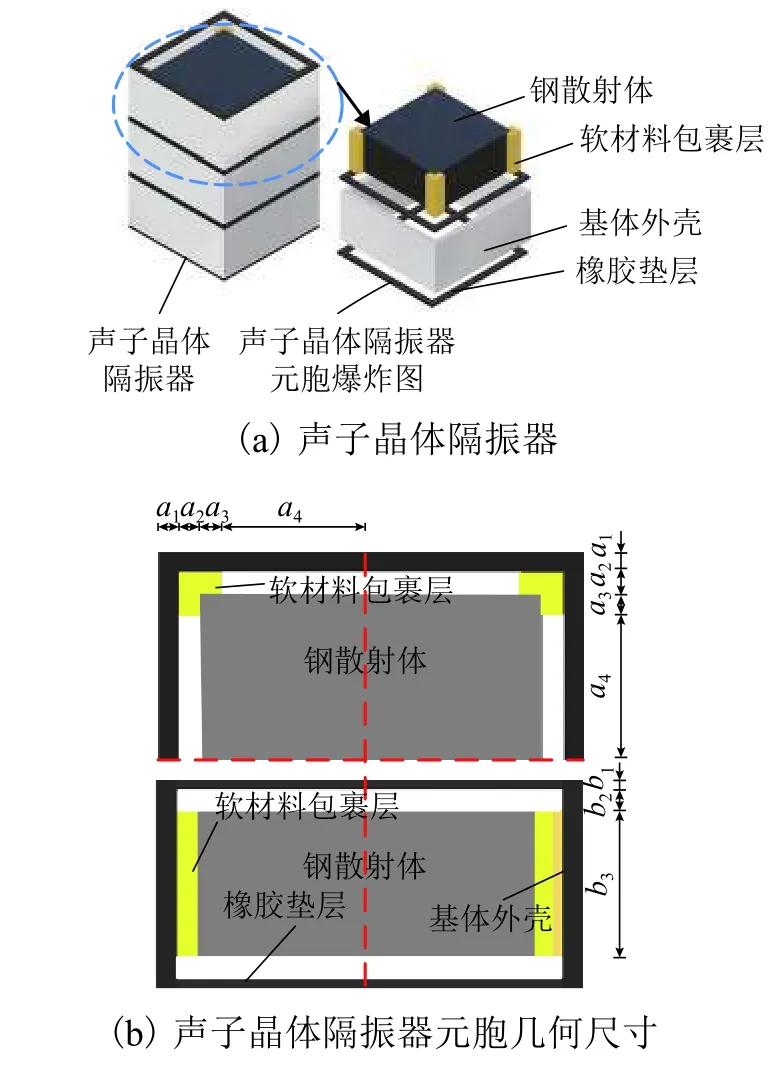
图 2 声子晶体隔振器结构Fig.2 Vibtration isolator structure of phononic crystals

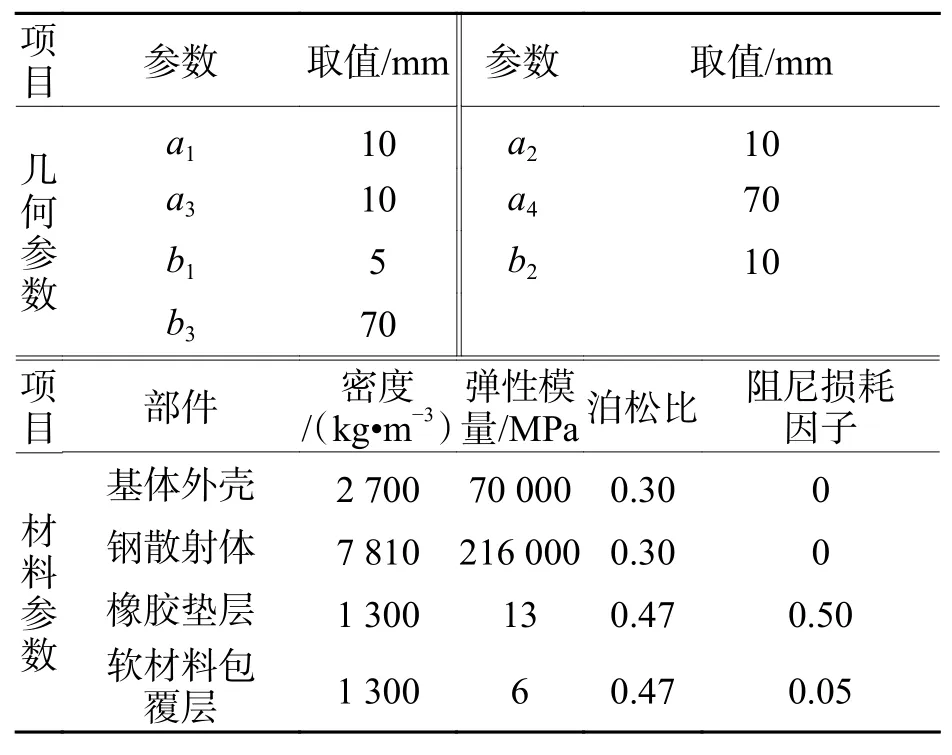
表 1 声子晶体隔振器元胞部分参数Tab.1 Some parameters related to vibtration isolators and its phononic crystal cell

2 声子晶体隔振器带隙特性

2.1 能带结构

当理想弹性介质（连续、均匀、各向同性及完全弹性）发生小变形时，其运动控制方程（不计体力）可表示为[12]

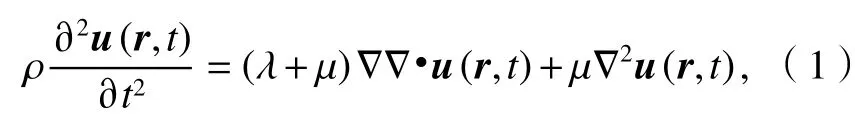
式中：u（r,t）为位移波函数；r为位置坐标；t为时间；ρ为密度；λ和μ为 Lamé常数； ∇ 为 Hamilton微分算子.

式（1）中的解满足 Bloch定理[13]：

式中：K为倒空间内的波矢（一维声子晶体为k）；uK（r）为波幅.由于结构的周期性，uK（r）可表示为周期函数[14]：

式中：R为正格矢.将式（3）代入到式（2）可得周期性边界条件：

将位移波函数和周期性边界条件代入控制方程，可得到包含波动频率与波矢关系的特征值，即能带结构[15].声子晶体隔振器能带结构可通过有限元软件COMSOL Multiphysics计算求得，对图2所示的元胞结构进行实体建模，在元胞上下截面设置周期性边界条件，令波矢扫描一维声子晶体不可越 Brillouin区边界（0，π/b），b为元胞晶格常数，b= 2b1+ 2b2+b3，计算不同波矢下的特征频率.为了减小网格尺寸对100 Hz以下计算结果的影响，最大单元网格尺寸不超过0.01 m.声子晶体隔振器前10阶能带结构曲线计算结果如图3所示.

图 3 声子晶体隔振器能带结构Fig.3 Band structure of vibration isolators of phononic crystals

对于图3所示的能带结构，尽管所有能带曲线均表征传播方向为轴向的导波，但并非所有导波的振动方向为轴向.当k= π/b时，声子晶体隔振器前10阶导波模态如图4所示.

图 4 声子晶体隔振器前10阶导波模态Fig.4 First 10th guided wave modal of isolators

图 5 振动方向为垂向的声子晶体隔振器能带结构Fig.5 Band structure of isolators with vibration in the vertical direction

由于地铁减振措施主要针对垂向振动，因此在研究声子晶体隔振器带隙特性时，应筛选振动方向为垂向的导波模态[16].筛选后的能带结构如图5所示.由图5可知，声子晶体隔振器第一带隙起始频率fs为 51 Hz，对应的k= π/b；截止频率fe为 147 Hz，对应的k= 0.波矢即波数矢量，表示单位长度内的波数，波数与波长对应，因此k= π/b对应波长为晶格常数一半的弹性波，k= 0对应弹性波长为无穷大的弹性波，两个波长下的垂向导波模态即为带隙的起始与截至模态.

2.2 边界频率

为了探究声子晶体隔振器的带隙特性，计算了决定第一带隙边界频率的共振模式，如图6所示.

图 6 第一带隙起始频率共振模态和截止频率共振模态Fig.6 Resonance modes at start frequency and cut-off frequeny of the first bandgap

由图6可知，决定起始频率的共振模式表现为相邻钢散射体带动软橡胶包覆层发生反相位共振，而基体外壳与橡胶垫层振动较小，整个结构在此共振模式下实现动态平衡，因此起始频率fs约等于钢散射体的共振频率.

2.3 带隙特性验证

声子晶体隔振器振动带隙的计算是在无限周期的条件下进行的，由于隔振器实际尺寸的限制，而本文中的声子晶体隔振器实际周期数为3，需利用传输特性[17]刻画其实际隔振效果，对带隙特性进行验证.由于声子晶体隔振器为一维周期结构，故在隔振器上端施加简谐加速度激励，计算下端加速度响应，通过式（5）求得声子晶体隔振器的加速度传递率（T），分析其传输特性，如图7所示，图中，Xin和Xout分别为输入和输出激励.

图 7 声子晶体隔振器传输特性有限元计算模型Fig.7 Finite element model for transmission characteristics of isolators

式中：aout和ain分别为输出端和输入端加速度幅值平均值，以传递率数值小于0的限界确定振动传递的衰减频段.加速度传递率是利用有限元软件COMSOL Multiphysics进行计算的，计算结果如图8所示.

图8中的虚线和实线分别表示无阻尼和有阻尼（同时包含内层和外层橡胶阻尼）时的传递率计算结果.当不考虑阻尼时，振动衰减频率范围为51～147 Hz；考虑阻尼时，振动衰减频率范围为48～147 Hz.比较图5和图8可知，通过能带结构得到的带隙频率范围和通过传递率得到的振动传递衰减频段吻合较好.

图 8 声子晶体隔振器频响函数Fig.8 Frequency response function of isolators

3 声子晶体隔振器浮置板轨道整体减振效果计算

为了验证声子晶体隔振器在浮置板轨道中的减振效果，并且与普通钢弹簧浮置板轨道的减振性能进行对比，取相同刚度的钢弹簧与声子晶体隔振器分别进行计算，进行对比分析.

3.1 声子晶体隔振器垂向静刚度

声子晶体隔振器作为结构部件，需为浮置板道床提供垂向刚度.为了保留传统钢弹簧浮置板轨道的隔振效果，声子晶体隔振器的垂向静刚度需与钢弹簧隔振器的垂向静刚度一致.相关文献表明[18]，钢弹簧隔振器垂向静刚度实测为6.0 kN/mm左右.

本文采用有限元软件计算声子晶体隔振器垂向静刚度.固定约束声子晶体隔振器下端面，在上端面施加垂向静荷载F，计算上端面的平均位移D，声子晶体隔振器垂向静刚度由表达式F/D而得.

经计算，声子晶体隔振器垂向静刚度为6.0 kN/mm，与钢弹簧隔振器的垂向静刚度相近.

3.2 声子晶体隔振器浮置板轨道整体减振效果

图 9 声子晶体隔振器浮置板轨道三维轨道模型Fig.9 Three-dimensional floating slab track with isolators

声子晶体隔振器浮置板整体减振效果为振动传递衰减效果和隔振效果的叠加.为了探究声子晶体隔振器浮置板整体减振效果，本节建立了三维轨道模型，如图9所示.由于模型沿纵向的长度有限，为了减少反射波对计算结果的影响，在钢轨和浮置板的两端施加低反射边界条件.在整个模型正中位置处的跨中钢轨轨头施加简谐垂向力Fin=F0eiωt（F0为垂向力的幅值），经计算提取最近声子晶体隔振器传递至下部基础的力Fout.通过计算力传递率（force transfer rate，

FTR）rFTR来反映声子晶体隔振器浮置板轨道整体减振效果：

当力传递率较小时，浮置板轨道即有着较好的减振效果.采用有限元法求解上述模型，所有轨道部件均采用实体建模，划分的有限元模型如图10所示.

图 10 有限元模型网格Fig.10 Finite element meshing of the model

同样，本节对传统浮置板轨道建立了三维轨道模型，计算其力传递率，用以对比声子晶体隔振器浮置板轨道的计算结果.计算时，钢弹簧隔振器采用弹簧单元模拟，垂向刚度为6.0 kN/mm，这与声子晶体隔振器垂向静刚度相同.上述模型的计算参数如表2所示.

声子晶体隔振器浮置板力传递率计算结果如图11所示.由图11可知，两条力传递率曲线均在25 Hz处与97 Hz处出现波峰，这是因为此频率下浮置板轨道发生弯曲共振.当频率高于25 Hz，两种轨道结构的力传递率随着频率的增大而逐渐减小.由于声子晶体隔振器和钢弹簧隔振器的垂向静刚度相同，38 Hz以下的力传递率几乎一致.

表 2 模型计算参数Tab.2 Model calculation parameters

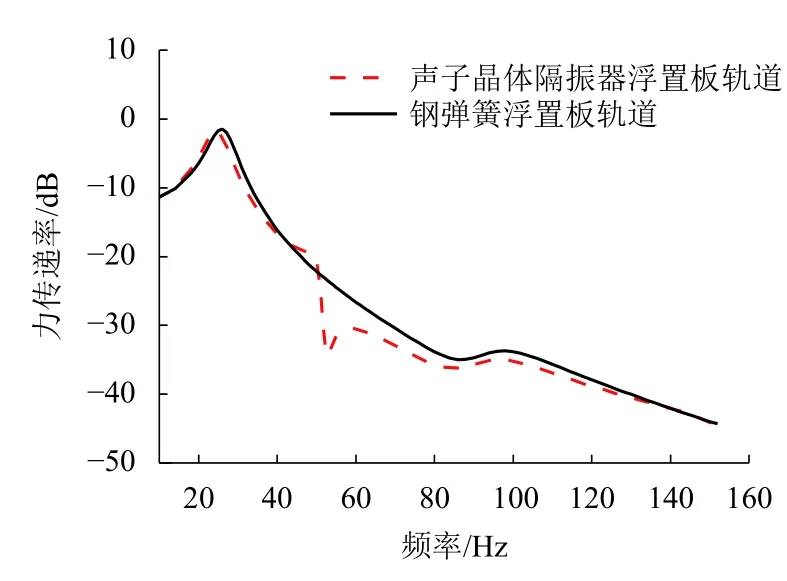
图 11 力传递率计算结果Fig.11 Calculation results of force transmissibility

为了进一步评价声子晶体隔振器与钢弹簧浮置板轨道的减振效果，建立考虑基础参振的动力学模型进行同样冲击荷载作用下的减振性能对比分析，轨道部分模型材料参数与边界条件同上述整体轨道模型，仰拱部分参数如表3，为了加快计算效率，整体模型采取轨道结构的一半，采用对称边界条件，整体模型示意图如图12.

在整个模型正中位置处的跨中钢轨轨头施加脉冲荷载，经计算提取最近声子晶体隔振器传递至下部基础的振动.通过对比声子晶体隔振器浮置板轨道与钢弹簧浮置板轨道传递至下部基础的加速度来评价其减振性能，图13（a）为下部基础振动加速度时域计算结果对比，图13（b）为下部基础振动加速度频域结果的对比.

表 3 仰拱部件计算参数Tab.3 Calculation parameters of invert components

图 12 考虑基础参振的整体计算模型Fig.12 Overall calculation model with base vibration

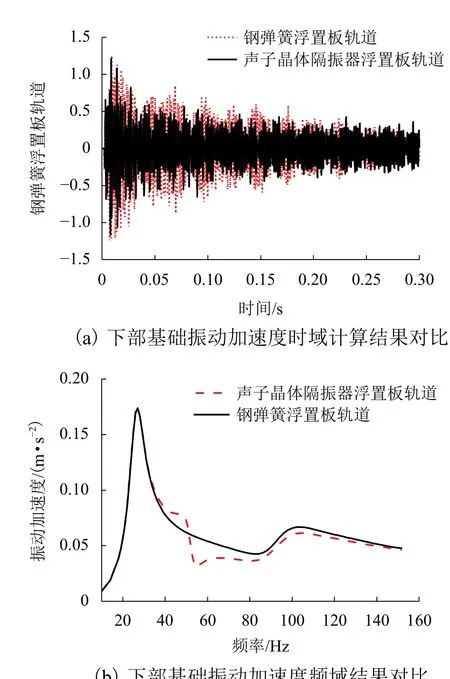
图 13 下部基础振动加速度时频域计算结果Fig.13 Frequency-domain results of the vibration acceleration for lower base

由图13（a）可知，声子晶体隔振器浮置板轨道下部基础的振动加速度在大多数时间段内小于钢弹簧浮置板下部基础的最大振动加速度，说明声子晶体隔振器浮置板轨道具有一定的减振效果；由图13（b）的频域结果可知，在51～150 Hz带隙范围内，相比普通钢弹簧浮置板轨道具有更好的减振效果，且在51 Hz附近，减振效果最佳.

由于声子晶体隔振器具有振动传递衰减特性，在50～129 Hz频率范围内，声子晶体隔振器浮置板轨道的力传递率低于传统浮置板轨道，说明其减振效果得以加强.在51 Hz处声子晶体隔振器与传统钢弹簧浮置板力传递率相比，可减小10 dB左右，在整个声子晶体带隙范围内，有60%频带范围内相比钢弹簧浮置板可减小2 dB以上.且声子晶体隔振器可以通过参数优化，实现对减振效果增强频率范围的精准控制.

4 结 论

本文提出了一种基于局域共振带隙机理的声子晶体隔振器，并将其应用于地铁浮置板轨道结构中.本文主要结论如下所示：

（1）声子晶体隔振器第一带隙的起始频率主要由钢散射体的共振决定，截止频率主要由钢散射体与软材料和基体材料所组成的联合体的反相位共振决定；

（2）声子晶体隔振器所提供的垂向刚度与第一带隙频率范围是相互独立的；声子晶体隔振器的振动传递衰减特性以及带隙频率范围可以通过修改材料进行控制，从而可以满足更多工程的减振需求；

（3）将声子晶体隔振器与钢弹簧分别应用于浮置板轨道计算其力传递率与基础的振动加速度，表明新型浮置板轨道相比传统钢弹簧浮置板轨道，可提供与传统钢弹簧相近的垂向刚度，在保留传统钢弹簧浮置板轨道低频隔振性能的前提下，进一步抑制低频带隙频率范围内纵波从道床板向基底的传播，与传统钢弹簧浮置板力传递率相比，在51 Hz左右可减小10 dB左右，带隙其余大部分可减小2 dB左右.

致谢：感谢广州地铁设计研究院股份有限公司“基于声子晶体理论的新型减振降噪措施理论与试验研究”研发项目支持.