基于分形表征的粗糙微纳米孔隙瓦斯气体传输方程
王登科,李文睿,魏建平,4,于 充,张凯旋
(1.河南理工大学 河南省瓦斯地质与瓦斯治理重点实验室-省部共建国家重点实验室培育基地,河南 焦作 454000; 2.中国矿业大学 深部岩土力学与地下工程国家重点实验室,江苏 徐州 221116; 3.河南理工大学 安全科学与工程学院,河南 焦作 454000; 4.煤炭安全生产河南省协同创新中心,河南 焦作 454000)
多孔介质中流体的质量传递、渗透率、流动阻力和扩散性能均与介质内部的微观结构密切相关。煤作为一种具有从微孔到大孔范围的多孔介质材料,其内部流体的传热传质一直以来都是研究的热点和难点。由于煤体内部存在有机质和无机质分布的不均匀性,流动通道呈现出复杂多变的结构特征,多采用理想水动力管束模型和宏观流动方程研究气体传输机理,难以对真实孔隙流动通道内的传输机理进行准确定义,随着科研技术的不断进步,这一限制条件正在被打破,已有专家学者采用先进的SEM[1]、显微CT[2]、3D打印[3-4]和原子力显微镜[5]等技术手段对煤体、页岩和砂岩内部孔裂隙结构进行了定性和定量描述。此外,已有学者证明多孔介质煤岩材料内部的孔隙结构可以采用分形几何理论进行表征,辅以计盒法可求得其分形维数[6-7]。XU和YU[8]的研究结果表明孔隙结构不仅是分形的,而且分形维数还可表示为结构参数的函数;并在此基础上建立了多孔介质孔隙毛细管束分形模型,用于多孔介质的分形维数与渗透率、扩散系数之间关系的研究。此外,基于随机分形Menger海绵体模型[9],王恩元和何学秋还建立了煤岩孔隙结构的随机分形模型[10]。李子文等[11-12]研究发现,只有当孔隙压力低于10 MPa时以压汞法测量出的孔隙才具有随机分形模型的特征,此时对应的孔隙半径约为60 nm。郑仟[13]、员美娟[14]、李玉丹[15]、王洪磊[16]等通过理论和实验研究表明,毛细管束分形模型对孔隙结构的表征更加准确且适用的孔隙尺寸范围更广,由此建立的多孔介质内部流体渗透率模型也更加准确[17]。国外学者通过类比孔隙结构分形,发现孔隙内部表面粗糙元或者接触点也满足一定的分形标度规律[18-19]。杨姗姗[17,20]建立了锥体的粗糙元分形模型,得到了摩擦因子和泊肃叶数的分析解模型,并讨论了孔隙结构参数对泊肃叶数的影响,这使得微观孔隙结构的分形研究得到了进一步的发展和延伸。
笔者以粗糙微通道中孔隙形态和内壁粗糙元分形分析为基础,推导了粗糙微纳米孔隙中的瓦斯气体传输方程,将瓦斯气体等效视渗透率模型与实验结果进行对比,从孔隙结构参数的精确求解和分子流动机理两方面印证了笔者所建瓦斯气体传输方程的合理性和准确性。
1 煤样孔隙结构实验结果
利用河南理工大学的JSM-6390LV扫描电镜(图1)对煤样的孔隙进行了扫描,结果如图2所示。

图1 JSM-6390LV扫描电镜
根据电镜扫描得到的煤体孔隙内部具体形貌细节(图2),可以发现煤的孔隙及其内部粗糙结构与纳米管束分形模型的基本假设相吻合[21]。因此,借鉴前人的研究成果[22],可将孔隙通道简化为圆管,内表面粗糙元以简化后的半球体代替,如图3所示,并可按照分形标度定律通过结构参数分形对孔隙和粗糙元进行分形表征。

图2 煤中粗糙孔隙微通道形貌结构
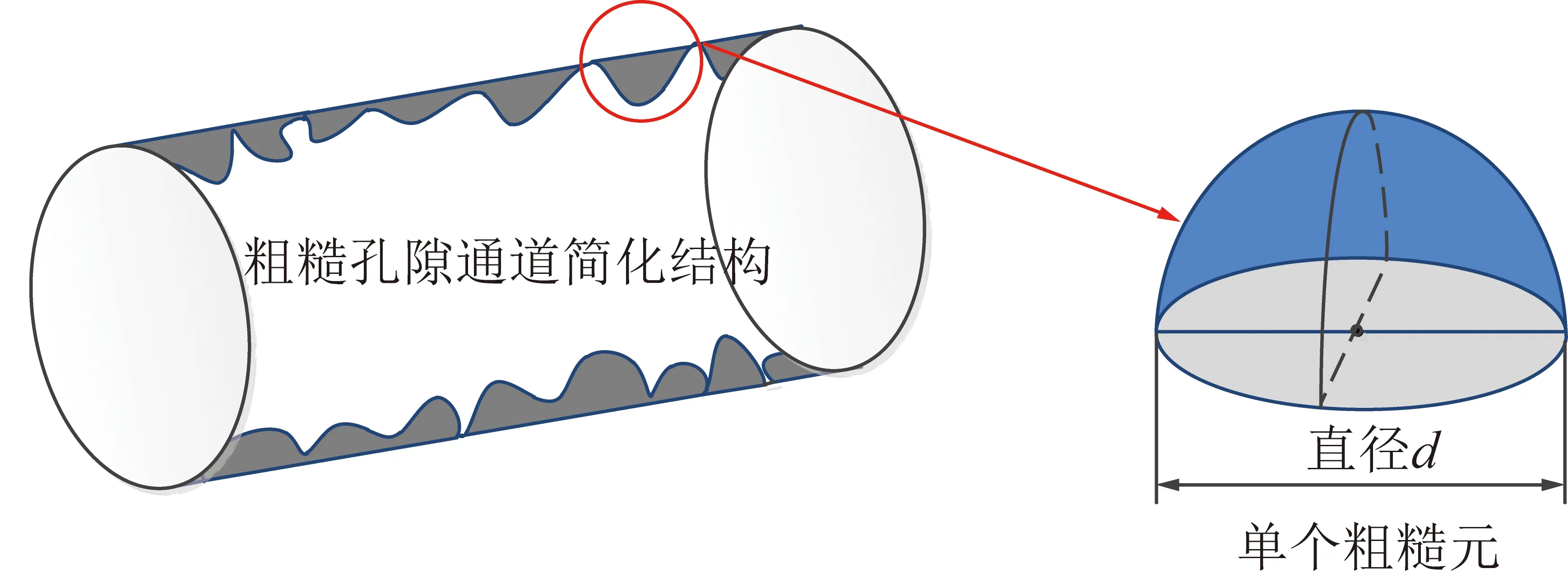
图3 煤中孔隙微通道结构简化模型
2 粗糙微通道的分形表征
2.1 孔隙分布的分形表征
YU[23]的研究表明,多孔介质中孔隙孔径分布与孔隙结构满足分形特征,孔隙数量分布函数表达式为
N(≥dp)=(dm/dp)Df
(1)
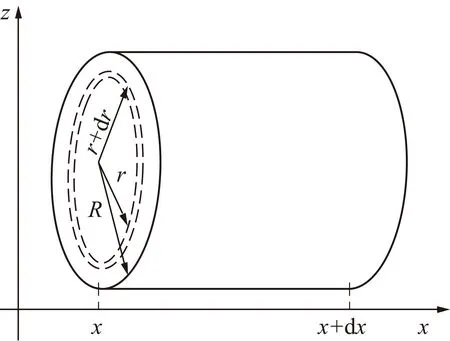
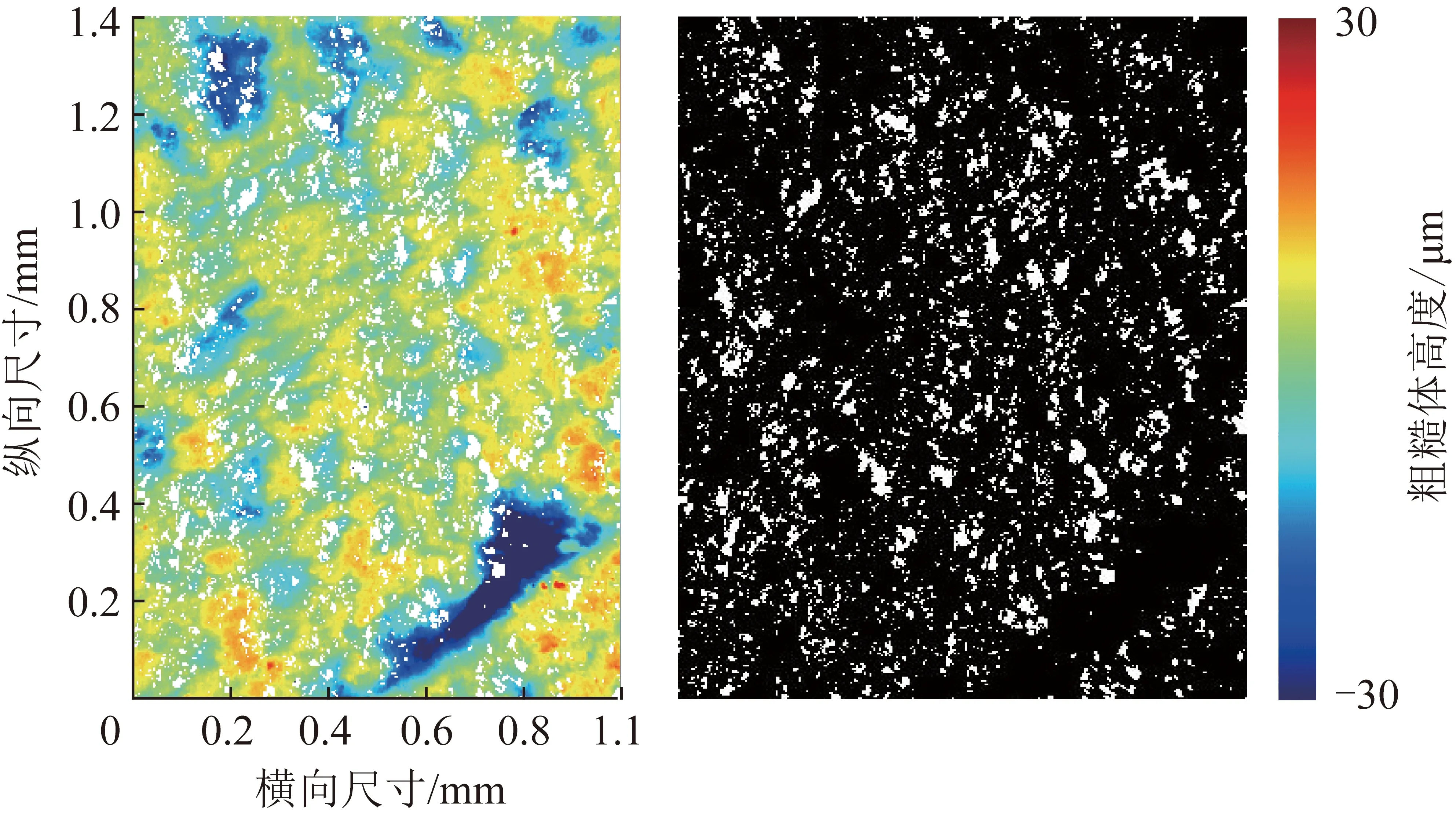
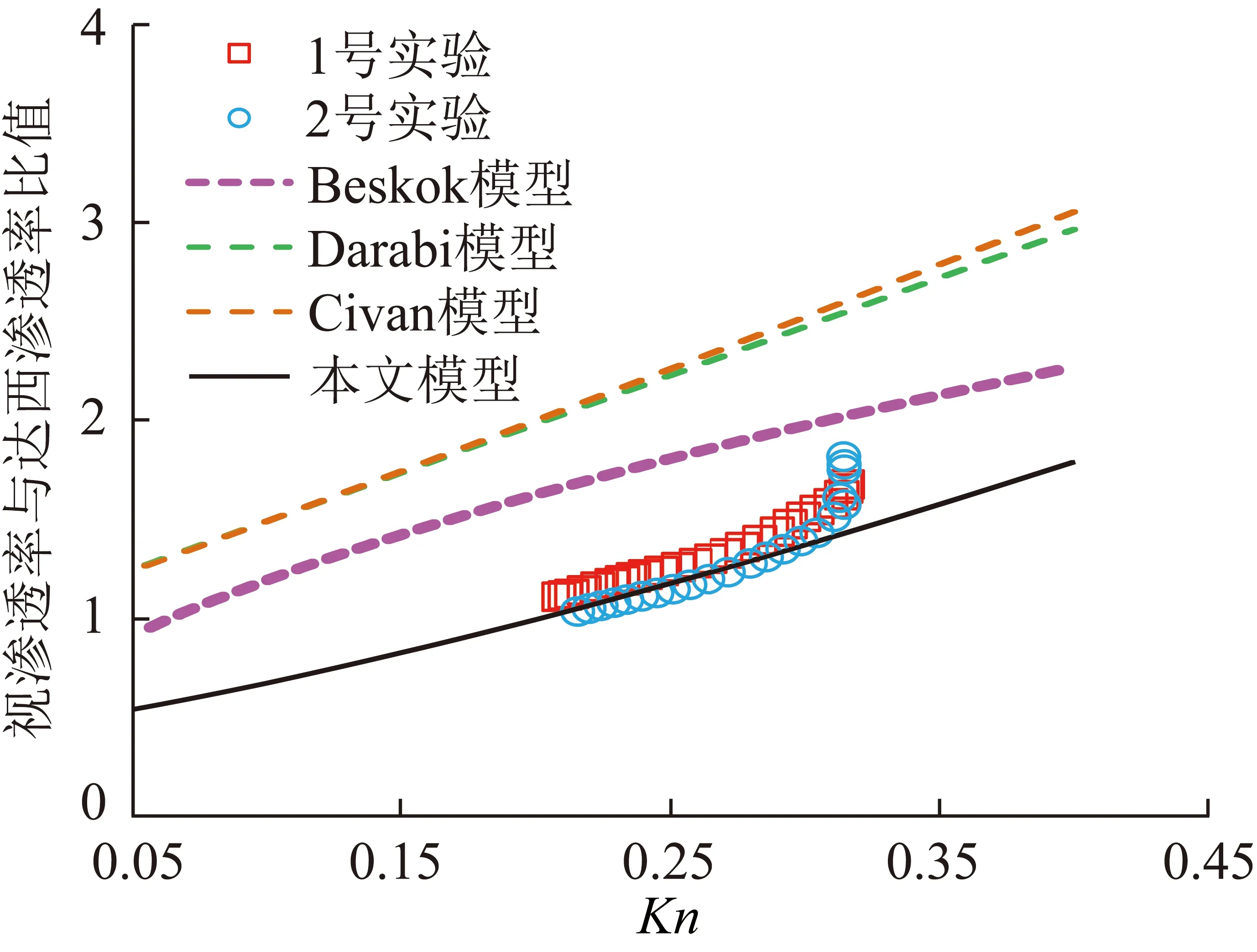
式中,dp为多孔介质纳米孔的直径,m;N为直径≥dp的孔隙数量;dm为多孔介质孔隙直径最大值,m;Df为孔隙直径的分形维数,在二维和三维空间内的取值分别为0 在式(1)中可把孔隙数量表达式看作一个连续的可微分函数,则直径为dp~(dp+ddp)的孔隙数量为 (2) 式中,-dN>0 表明孔隙数量随着孔隙半径减小而增加的关系。 对于具有自相似特征的孔隙结构,其直径大小[23]可用式(3)计算孔隙分形维数 (3) 式中,χ为欧几里德维数,在二维平面中χ=2,在三维平面中χ=3;φ为多孔介质的孔隙度,%;σ为孔隙最小直径与最大直径之比。 对于粗糙元底面直径大小的分形维数表达式可类比于式(3),但粗糙元的分形维数D的取值为0 (4) 式中,ε为孔隙粗糙体微元底面直径的最小值与最大值之比,ε=dmin/dmax;φ′为在一个分形集合中,所有半球体的底面总面积占整个分形集合单元总面积的百分数。 同理,直径为dr~d+ddr的粗糙元数量为 (5) 其中,dr为粗糙元底部直径,m;dmax为粗糙元底部直径最大值,m;N′为直径≥dr的粗糙元数量;-dN’>0 表明粗糙元数量随着孔隙半径减小而增加的关系;D为粗糙元的分形维数。 一个分形集合的单元中所有半球体的体积可以通过从最小粗糙元到最大粗糙元的积分求和得到: (6) 一个分形集合单元中所有半球体的底面积总和为 (7) 这里,考虑到孔隙直径属于二维平面,所以χ=2。将式(5)代入式(7)中,可得到 (8) 因此,由式(8)可得出一个孔隙结构单元中的总面积为 (9) 所以,在孔隙内部半球体粗糙元的有效平均高度为 (10) 微孔隙通道中的瓦斯气体传输不同于传统的水动力学流体传输规律。尤其当微通道孔隙的孔径与瓦斯气体分子自由程处于同一数量级时,瓦斯气体分子与孔隙壁面之间的碰撞愈发剧烈,气体稀薄效应也更加显著,其流动速度明显受到孔隙结构影响[25-26]。因此,学者们提出了以Maxwell分子碰撞散射模型去揭示稀薄气体分子在微通道孔隙中的真实传输情况。其基本思想为:分子的碰撞运动由两种反射组合而成,假设来流分子中发生漫反射的部分为t,则剩余部分发生镜面反射。 假设w0是气体相对于壁面的速度,则在流动方向存在法向速度梯度,dw/dz,法向方向速度为 (11) 另外,根据Maxwell散射模型可得孔壁表面分子速度w0为 (12) 联立式(11)和(12)可得 (13) 需要说明的是,在微孔隙中,除了分子与壁面的碰撞以外,分子与分子之间还发生着不同程度的碰撞。热力学理论认为,单位时间内分子碰撞的次数等于分子与分子之间碰撞次数与分子与壁面碰撞次数之和[27],因此可得出 (14) 式中,T1为单位时间内分子与分子碰撞消耗的时间;T2为单位时间内分子与壁面碰撞消耗的时间;Ttotal为分子碰撞的某一单位时间。 假设分子发生碰撞的初始热运动速度均为v,则各形式碰撞次数可表示为 (15) 式中,λ为气体分子平均自由程;r为圆管半径。 将式(15)代入(14)中可得 (16) 由此,可以得到分子与壁面的碰撞次数占总碰撞次数的比例系数c为 (17) 其中,Kn为克努森数,等于分子平均自由程与孔隙半径之比,无量纲,Kn越大表示气体传输过程中分子碰撞越剧烈。 在式(11)中分子碰撞后在法相方向上的位移可表示为 (18) 进一步,将式(18)代入式(13)可得粗糙微通道壁面分子的速度为 (19) 如图4所示,在圆柱径向x~x+dx,轴向r~r+dr方向流体受到壁面的切应力为 (20) 式中,μ为气体动力黏度,Pa·s。 图4 圆管内微元体传输结构 (21) 根据式(21)进行一次积分后可得到 (22) 通过对式(22)进行再次积分进一步得到孔隙流体速度 (23) 当r=0时,壁面分子流速为定值,则a=0;当满足真实孔隙半径大小边界条件,即式(19)中r=R时,通过联立式(23),管壁面的速度满足: (24) 由此可得常数b为 (25) 再将式(25)代入式(23)进而可得到微通道内某一质点的流体速度表达式 (26) 当某一孔隙半径为定值r0时,通过单个微通道的体积流量可以表示为 (27) 根据孔隙通道的真实情况,在此对气体传输通道的有效半径进行细化可得 (28) 式中,re为粗糙孔隙微通道内的有效半径,m。 因此,微通道内具有滑移流效应的平均流速可表示为 (29) 相应地,考虑到真实气体效应影响,孔隙微通道内的质量流量可以表示为 (30) 式中,J为粗糙孔隙微通道内的气体质量通量,kg/(m2·s);Q为气体体积流量,m3/s;ρ为游离瓦斯气体真实密度,kg/m3。 同时考虑到多孔介质的孔隙率影响,式(30)气体质量通量方程可转化为等量视渗透率为 (31) 式中,Ks为连续性滑流气体传输等量视渗透率,m2;φ为多孔介质孔隙率,%。 受煤体内孔径连通性的影响,孔隙压力处于一个动态松弛变化的过程,导致孔隙内的气体扩散传输呈现出由瞬态激发到缓慢衰减的一个漫长过程[28]。若不考虑煤的理化性质对气体吸附性能差异性的影响[29],单纯研究孔隙内可流动气体的传输特性就变得直观具体,仅就某一孔隙作为气体流动通道载体来说,稳定压力梯度驱动下的气体扩散传输可通过理论公式进行定量研究。 对于非连续流的分子扩散传输,主要以分子间碰撞和分子与壁面碰撞两种形式存在。在两种分子扩散同时存在情况下,以浓度梯度为驱动力的扩散传输通量方程[25]可表示为 (32) 同理,气体扩散质量通量传输方程式(31)转化为等量视渗透率为 (33) 式中,Kd为分子扩散传输通量的等量视渗透率,m2。 将滑流方程和扩散方程的等效视渗透率相加即可得到纳米孔气体传输统一视渗透率数学模型: (34) 式中,Kapp为考虑粗糙孔隙分形特征的瓦斯气体传输统一视渗透率,m2。 对于未经修正的多孔介质固有渗透率,其表达式为 (35) (36) 对于A的取值,AGRAWAL和PRABHU[30]系统性的研究了参数A中t的取值,建议取值为0.9较为合适,即A=11/9;此后,DARABI[31]等经过数值模拟、计算分析与实验对比验证了取值的合理性,因此在下文模型计算过程中则直接取该值代入计算。 图5 粗糙形貌的3D扫描成像仪 利用河南理工大学的Optical Tensiometer设备(图5)对取自煤体孔隙内壁的煤片进行微米级3D形貌结构扫描分析,利用自带的OneAttension软件进行详尽的定量化表征,二维成图效果如图6所示,三维成图效果如图7所示。 图6 煤体孔隙壁面粗糙形貌结构 图7 孔隙壁面粗糙体三维分布特征 图6中左图为粗糙表面二维结构图,右图为对应的图片二值化处理结果。在二维平面中,图中白色斑点部分为光滑无粗糙区域,暗部为粗糙结构分布区域,通过MATLAB编程技术求得粗糙元投影底面总面积占整个平面比例φ′为77.08%。由于在二维孔隙直径内部粗糙元分形维数D=2表示粗糙元铺满整个平面,所以此处根据77.08%比例关系求得对应D=1.541 6。 图7中以粗糙体峰值0高度作为孔隙壁面分割基准面,以上部分为上凸粗糙体,以下为下凸粗糙体。由于第2节中将粗糙体假想为半球微元体,所以粗糙体微元底面直径最小值与最大值之比ε就转化为粗糙元高度之比。在实际岩石孔隙中,存在孔隙内壁粗糙元直径大小与孔隙半径相当,此时粗糙元最大直径dmax即为孔隙半径。因此,在φ′=77.08%,D=1.541 6,dmax=r的赋值条件下,可求出相对粗糙度值,求解公式为 (37) 为便于计算这里将粗糙元最低轮廓(图7中浅色部分所构成的宏观轮廓)偏离基准面的算术平均值作为粗糙体理想化最小高度值(该值由设备自带的OneAttension软件处理得到),相对粗糙度计算结果见表1。 表1 壁面粗糙结构的参数信息 Table 1 Parameters about the structure roughness of inner surface in pore 表面轮廓偏离分割基准面的算术平均差/μm最大峰值/μm粗糙元高度之比ε相对粗糙度γ4.17446.2630.0090.352 本文所提出的相对粗糙度计算公式(式(37)),相较于DARABI等[31]提出的孔隙粗糙度经验性表达式(分子直径与孔隙局部直径比值的指数式修正系数,见表2中Darabi模型),以真实孔隙简化后的微结构分形几何解析表达式,更能直观反映出煤体中微纳米孔隙的结构参数,能更好地反映粗糙元底面直径、排布方式、内壁面积覆盖度等因素对气体传输通道有效半径的影响。 对于孔隙瓦斯气体传输方程,采用等效的渗透率方程验证是最为直接有效的方法[32]。因此,在未经修正的多孔介质固有渗透率模型基础之上,学者们又提出了多种较为精确的视渗透率模型,具体见表2。 本文孔隙渗透率验证实验步骤为:首先以纳米薄膜材料为孔隙载体,通过SEM扫描技术对纳米孔隙薄膜孔径分布进行表征(图8);然后利用MATLAB对图片进行二值化处理求得孔隙率(参数见表3);并利用河南理工大学PMI微渗透测试设备(图9)进行渗透率实验。最后,将本文视渗透率模型和几种典型视渗透率模型的计算结果与实验结果进行对比,对比结果如图10所示。 表2 几种典型孔隙流体的视渗透率模型 Table 2 Several typical apparent permeability models of gas flow in pore 模型简称视渗透率模型数学表达式阐述Darabi模型[31]Kapp=éëêê1+4AKn+64φKn3τπδr()Df-2ùûúúKDacy,δr()Df-2为考虑粗糙度影响的修正系数,Df=2.5,孔隙迂曲度τ=2.2,甲烷分子直径δ=0.38nmCivan模型[32]Kapp=[1+β(Kn)Kn]1+4Kn1+Kn()KDacy,β(Kn)=6415π1+0.199Kn0.365()Beskok模型[33]Kapp=[1+α(Kn)Kn]1+4Kn1+Kn()KDacy,α(Kn)=12815π2arctan(4Kn0.4) 图8 纳米孔隙薄膜SEM图和对应的二值化图 表3 纳米薄膜物理特性参数 图9 纳米薄膜微渗透性测试设备 图10 理论模型与实验数据比较结果 不论是微米级的孔隙通道还是纳米级孔隙通道,其内部形貌结构在一定程度上都较为类似。PFUND等[34]通过微米级管道的流体分析,得出相对粗糙度随着孔隙尺度的减小而增大,孔隙壁面粗糙将对流体传输造成显著影响。图10中的模型对比结果有效验证了这一观点,相较于其他理论模型不考虑粗糙度影响或者采用粗糙度经验性公式的视渗透率模型,本文模型更加精确可靠。同时从图10中也可以看出,本文所建立的视渗透率传输模型与实验结果吻合效果良好,充分证明了用分形方法表征孔隙微观结构进而研究粗糙微纳米气体传输的合理性和准确性。 (1)以分形表征得到的微纳米孔隙的粗糙元有效平均高度,精细地反映了微纳米孔隙表面的粗糙结构机制,并且每个结构参数的物理意义明确,能够揭示影响有效孔隙半径的微观结构机制,这对于以分形拓扑理论构建自仿射粗糙微通道进行煤层瓦斯气体流动模拟研究具有重要意义。 (2)相较于直接在气体传输方程中采用粗糙度经验公式修正微纳米孔隙瓦斯气体传输通量的方法,利用粗糙形貌3D扫描成像设备,对孔隙粗糙表面微结构进行定量表征,所求得的相对粗糙度值更加科学可靠。 (3)所建立的基于分形表征的粗糙孔隙瓦斯气体传输方程综合考虑了孔隙粗糙度、气体速度滑移和分子扩散对瓦斯气体流动的重要影响,计算结果更为准确合理,有效揭示了瓦斯气体微观传输机制。2.2 孔隙内部粗糙元分形分析
3 粗糙孔隙内气体传输方程
3.1 滑移流动方程
3.2 非连续流气体扩散传输方程
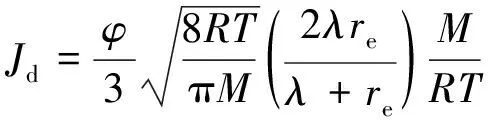
3.3 微纳米孔隙气体视渗透率模型
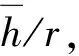

3.4 微纳米孔隙相对粗糙度的测试与求解


3.5 视渗透率模型验证性实验




4 结 论

