平台转动对SAR成像的影响分析
许 辉,孙英钦,安广锐,张一军
(1.西安应用光学研究所, 陕西 西安 710065; 2.苏州途视电子技术有限公司, 江苏 常熟 215536)
引言
合成孔径雷达(synthetic aperture radar,SAR)是一种高分辨对地成像雷达[1-3]。相比于光学成像,具有全天候、全天时、多波段、多极化、穿透性强等特点[4],在环境监测、地形测绘、战场侦察等方面有着重要应用[5-9]。
SAR一般都安装在运动平台(例如飞机、卫星等)上,匀速向前移动,以某个固定频率不断地向平台侧方发射脉冲信号并接收目标反射的回波,对回波进行相参处理后可获得目标的高分辨图像。SAR发射大时间带宽积脉冲信号,利用脉冲压缩技术实现距离向高分辨;SAR平台运动可以合成大孔径的等效阵列天线,从而获得方位向高分辨[10]。
由于受各种因素的影响,实际中SAR平台存在运动误差,包括[11]:1)平台沿航向的加速度不为0;2)平台的横向(即垂直于航向的方向)速度不为0;3)平台存在绕质心的转动,即偏航、俯仰和横滚3个方向的转动。前两项因素是平台偏离匀速直线运动的表现,在很多文献中都有讨论[12,16],而关于平台转动对成像效果影响的研究较少。分析了平台三轴转动对SAR成像质量的影响,首先对平台转动进行建模,然后从波束照射区域、回波幅度调制、回波相位调制等方面对平台转动的影响展开分析。
1 SAR平台转动模型
将SAR平台的转动分解为绕“3个相互垂直的坐标轴”的转动,即偏航、俯仰和横滚。以机载SAR为例,偏航指机头指向的沿水平向的变化,俯仰指机头指向的沿垂直向的变化,横滚指飞机绕其中轴线的转动,如图1所示。
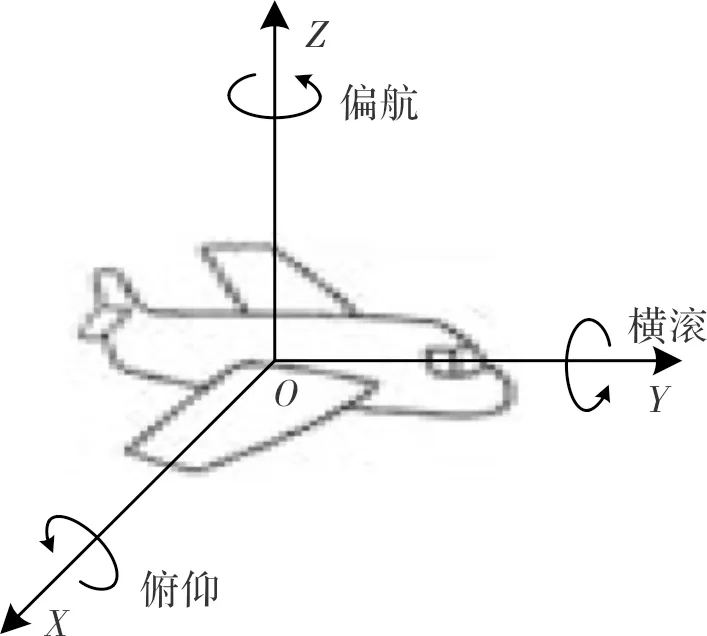
图1 平台转动模型Fig.1 SAR platform rotation model
SAR平台的转动可分解为多个正弦形式转动的叠加。以单一频率正弦转动为例,假定平台转动为正弦模型,即姿态角(偏航角、俯仰角、横滚角)满足如下模型:
θ=A·sin(2πft+φ0)+θ0
(1)
式中:A为正弦转动幅度;f为正弦转动频率;φ0为初相;θ0为姿态角均值。对(1)式求导,得到姿态转动的角速度为
ω=2πfA·cos(2πft+φ0)
(2)
对(2)式求导,得到姿态转动的角加速度为
(3)
因此在正弦转动模型下,姿态角变化的幅度为A,角速度最大值为2πfA,角加速度最大值为(2πf)2A。
为了更为直观地了解平台转动的量级,下面以某实验SAR平台为例给出了3个姿态角的具体模型。由于初相φ0对后面的分析基本没有影响,因此这里假定初相φ0=0。
偏航角模型
θyaw=3.6sin(1.67t)
(4)
俯仰角模型
θpitch=2.5sin(2t)+8.5
(5)
横滚角模型
θroll=3sin(4t)
(6)
注意:上述3个模型中姿态角的单位都是度。
2 平台转动对SAR成像的影响分析
平台转动对SAR成像的影响体现在3个方面。
1)改变雷达波束的照射区域
横滚角变化,会改变波束在距离向的照射区域;偏航角变化,会改变波束在方位向的照射区域。照射区域的变化可能会导致场景边缘的目标无法实现方位向完全积累。
2)回波产生幅度调制
姿态角变化时,会导致目标回波的天线加权变化,产生回波能量变化,即回波幅度调制。
3)回波产生相位调制
由于天线一般都安装在平台边缘,而平台都是绕其质心转动,所以平台转动会改变天线的相位中心位置,从而导致目标斜距变化,引入相位调制。
下面仍以某实验SAR为例对这3个方面的影响分别进行具体分析。该实验SAR采用裂缝天线单面阵形式,工作在条带成像模式下,其系统参数如表1所示。

表1 实验SAR系统参数Table 1 Parameters of experimental SAR system
为了验证理论分析结果,使用SAR回波仿真软件生成回波数据,并进行处理,将结果与理论分析进行对比。SAR回波仿真软件界面如图2所示。
图2 SAR回波仿真软件界面Fig.2 Interface of SAR echo simulation software
2.1 雷达照射区域的变化
当SAR平台横滚角变化时,天线波束的俯仰角会随之变化,导致雷达波足区域沿距离向发生改变,如图3所示。
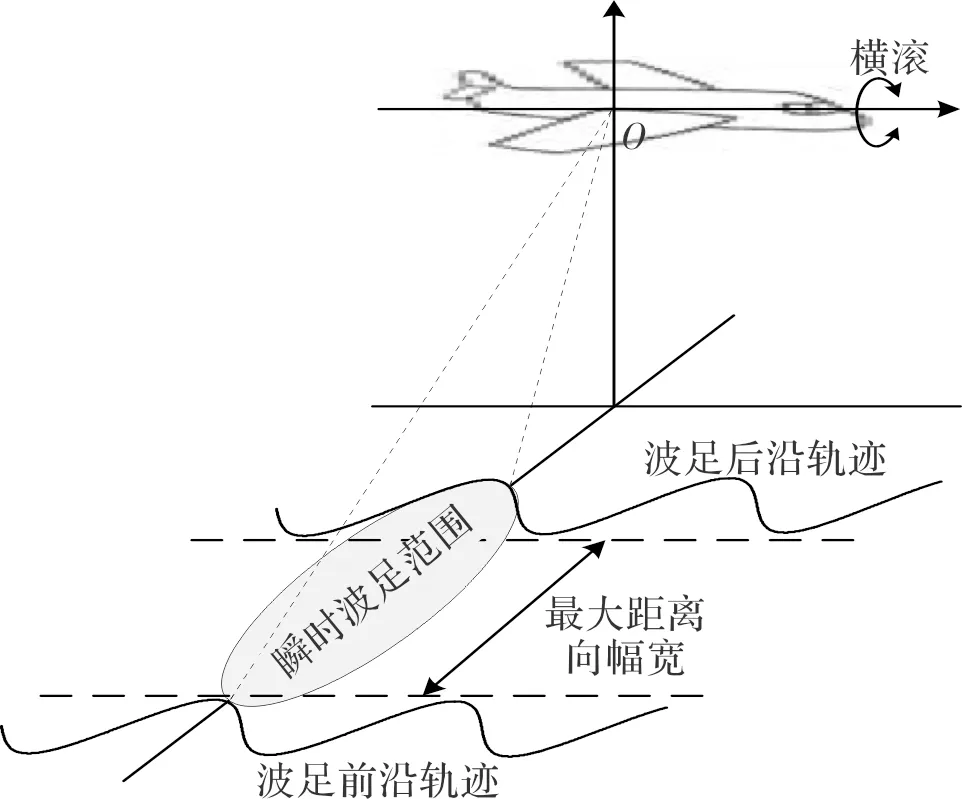
图3 SAR平台横滚角变化时的波束足迹Fig.3 Footprint of SAR when roll angle varies
假定横滚角速度为ωroll,在方位积累时间内,由于横滚角的变化导致天线俯仰角的变化占整个天线俯仰波束宽度的比例为
(7)
式中:Ts为方位积累时间;φE为俯仰波束宽度,该比例是由横滚角变化导致的距离向成像幅宽损失。为了保证整个成像区域在方位积累时间内都被雷达波足所覆盖,则最大的距离向成像幅宽为
(8)
式中:R为作用距离;β为SAR天线俯仰角。
类似地,当SAR平台偏航角变化时,导致雷达波足区域沿方位向发生改变,方位向成像幅宽损失为
(9)
式中:φA为方位波束宽度;ωyaw为横滚角速度,最大的方位向成像幅宽为
Wa,max=R(φA-ωyawTs)
(10)
针对该实验SAR系统,以最大的横滚角速度计算,得到方位积累时间内最大的横滚角变化为0.21°,距离向成像幅宽损失为12.1%。以高度40 km、作用距离80 km为例,距离向成像幅宽最大为4.3 km。
以最大的偏航角速度计算,得到方位积累时间内最大的偏航角变化为0.11°,方位向成像幅宽损失为3.5%。以作用距离80 km为例,方位向成像幅宽最大为4.1 km。
2.2 回波的幅度调制
由于方位积累时间较短,在这段时间内姿态变化尚未完成一个周期,因此回波幅度调制也未完成一个周期。这里将通过数值仿真的方法分析回波幅度调制对聚焦的影响。
由于天线俯仰波束宽度较窄,并且横滚角变化较快,因此俯仰向天线加权的变化最快,回波幅度调制最明显。因此这里主要分析俯仰向天线权值对回波幅度调制的影响。
假定俯仰向天线方向图为sinc函数形式,即双程的幅度加权为
(11)
式中β为目标视线偏离波束中心的俯仰角。图4给出了WE随β的变化曲线。

图4 俯仰向双程天线幅度加权曲线Fig.4 Echo amplitude weighted curve of two-way elevation beam
选择横滚角变化最快的时间段[-Tsmax,Tsmax]进行仿真。当目标位于俯仰波束边缘时,其幅度调制变化最大,因此假定目标位于俯仰波束边缘。此时,目标偏离波束中心的俯仰角β为
β=φE/2+3sin(4t)
(12)
图5给出了目标的回波幅度调制的结果,从图中看出回波幅度有约4 dB的变化。

图5 目标位于俯仰波束边缘时的回波幅度变化Fig.5 Echo amplitude change at elevation edge of footprint
图6给出了目标的方位脉压结果,通过与无幅度调制的结果对比,可以看出幅度调制对聚焦的影响很小。
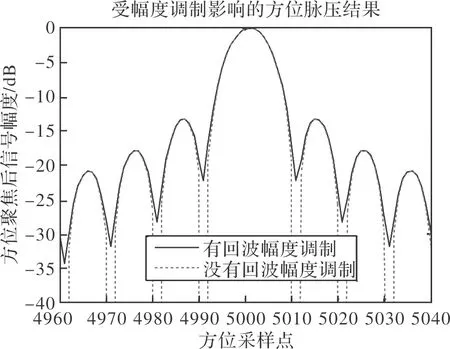
图6 目标位于俯仰波束边缘时的方位脉压结果Fig.6 Azimuth compression at elevation edge of footprint
2.3 回波的相位调制
平台转动会引起天线相位中心的变化,该变化受天线与平台质心的相对位置的影响很大。由于这里无法明确天线的相对位置,因此只考虑2种极端情况,第一种是天线相位中心与平台质心连线平行于雷达视线,第二种是天线相位中心与平台质心连线垂直于雷达视线方向,并且平台的旋转轴垂直于两者连线以及雷达视线。
假定天线相位中心与平台质心的距离为L。
1) 第一种情况
平台与目标的相对位置关系如图7所示。此时,目标回波的相位调制可近似表示为
(13)
由于方位积累时间相对于姿态角变化周期很短,因此在方位积累时间内,可以认为平台在匀速转动,即角度θ近似为
θ=ωt
(14)
因此,(13)式可以表示为
(15)

图7 第一种情况下几何关系示意图Fig.7 Geometric relation under case 1
即相位调制可以近似表示为二次相位。若要求二次相位小于π/4,则需要满足
(16)
式中取最大的角速度ω=12°/s,则得到L<288 m。
分别以L=5 m和288 m为例进行仿真,相位调制如图8所示。从图中可以看出,相位调制以二次相位为主。当L=5 m时,相位调制很小,只有约0.014 rad;当L=288 m时,相位调制约为0.81 rad,即0.26π,与理论计算值基本一致。
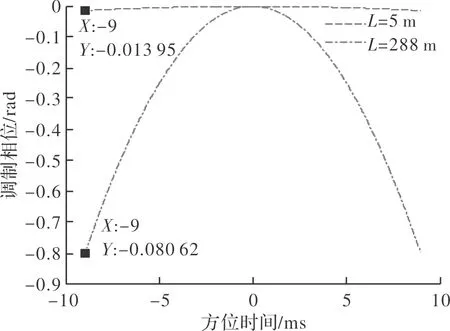
图8 第一种情况下的相位调制Fig.8 Phase modulation under case 1
对存在相位调制的信号使用SPECAN方法进行方位脉压处理,结果如图9所示。从图中可以看出,当L=5 m时,脉压结果与理想情况几乎相同,当L=288 m时,主瓣展宽只有1.36%,副瓣上升到-12 dB左右,如果对副瓣水平有要求,可以通过加窗技术将其抑制到较低水平。
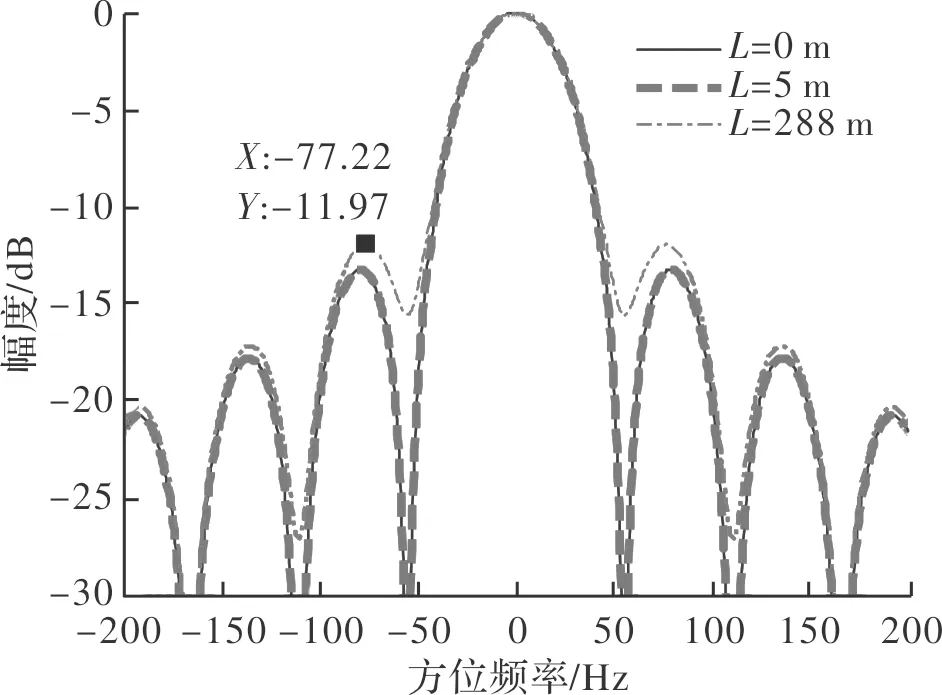
图9 第一种情况下的方位脉压结果Fig.9 Azimuth compression under case 1
2) 第二种情况
平台与目标的相对位置关系如图10所示。
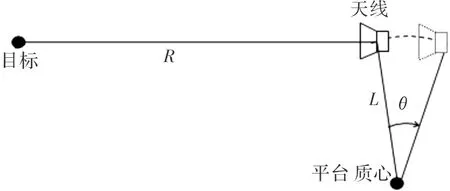
图10 第二种情况下几何关系示意图Fig.10 Geometric relation under case 2
此时,目标回波的相位调制可以近似表示为
(17)
即相位调制可以近似表示为一次相位,该一次相位会导致目标方位位置的偏移,偏移量为
(18)
式中偏移量δ以方位分辨单元长度为单位。若要求目标方位位置偏移小于一个方位分辨单元长度,则一次相位对应的频率应小于方位积累时间的倒数,因此L需要满足
(19)
取ω=12°/s,则得到L<1.07 m。
分别以L=1 m和5 m为例进行理论分析和仿真。取最大的角速度ω=12°/s,根据(17)式和(18)式可以计算,L=1 m时线性相位为2.96 rad,偏移量为0.94个方位分辨单元,L=5 m时线性相位为14.80 rad,偏移量为4.71个方位分辨单元。
通过仿真得到相位调制如图11所示,从图中可以看出,相位调制以线性相位为主。当L=1 m时,相位调制约为2.96 rad;当L=5 m时,相位调制约为14.79 rad,与理论计算结果相一致。
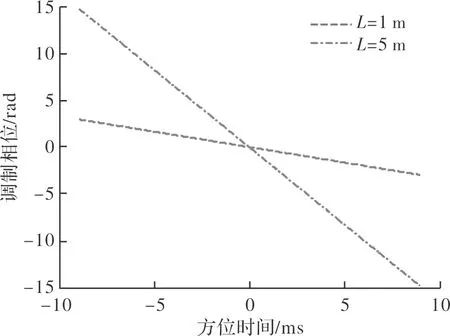
图11 第二种情况下的相位调制Fig.11 Phase modulation under case 2
对存在相位调制的信号使用SPECAN方法进行方位脉压处理,结果如图12所示。从图中可以看出,当存在相位调制时,脉压结果主要发生了平移,主瓣展宽和副瓣升高都很小。当L=1 m时,脉压结果相对于L=0 m的理想情况向左平移了约0.93个方位分辨单元,当L=5 m时,脉压结果向左平移了约4.68个方位分辨单元,与理论计算值一致。

图12 第二种情况下的方位脉压结果Fig.12 Azimuth compression under case 2
2.4 小结
对上述分析结果总结如下:
1)平台转动最大会导致12.1%的俯仰波束宽度和3.5%的方位波束宽度的成像幅宽损失;
2)平台转动引入的幅度调制对聚焦的影响很小,可以忽略;
3)平台转动引入的二次相位调制很小,可以忽略;一次相位调制会导致目标方位位置的偏移,在最极端的情况下,为了使偏移量小于一个方位分辨单元,需要满足天线相位中心与质心之间的距离小于1.07 m。
3 结论
分析了平台转动对SAR成像的影响,首先建立了平台转动的正弦模型,分析了转动幅度、角速度和角加速度之间的关系,然后从成像幅宽的变化、回波的幅度调制和回波的相位调制等3个方面进行了详细分析,分析结果可以为SAR系统设计和算法论证提供参考和约束。

