基于双镜反射法的亚角秒级小角度测量*

马 韬，王卫华，曹赫扬，吴刚祥

(1. 苏州大学 光电科学与工程学院·苏州·215006；2. 江苏省先进光学制造技术重点实验室&教育部现代光学技术重点实验室·苏州·215006；3. 上海航天控制技术研究所·上海·201109)

0 引 言

近年来，高分辨力微小角度测量理论、方法和技术发展迅速，进一步满足了更高精度的角振动、结构挠性形变、瞄准与定位等角度计量需求，对机械工业、航空航天、军事国防等领域的技术发展起着极为重要的促进作用[1]。

相对于机械式和电磁式等方法，光学测角方法具有精度高、非接触等优点，且方法种类多，可选择性大，应用更为广泛。根据测角方式的不同，光学测角方法可以分为直接测角法和位移解算测角法两种。直接测角法是测量值直接反映角度变化，角度实体的微小横移不会对测量结果有显著影响，如自准直法[2-3]、双镜反射法[4-5]、莫尔条纹法[6-7]、内反射反射比法[8]、内反射干涉相位法[9-10]等。位移解算测角法是测量角度实体的转动切向位移，再根据角度的转动半径计算相应的角度变化量，由于角度轴心位移不可忽略，必须同时测量不同位置的两个测点的切向位移，再根据两个测点的切向位移差值与间距进行角度解算，如激光外差干涉法[11-12]、共焦显微镜法[13-14]、白光干涉法[15]等轴向测距法。

本文介绍的测量方法是通过双平面镜多次反射，激光束出射角度增量随反射周期数2倍放大，从而获得较大的激光光斑位移，实现微小角度的测量，具有结构简单、分辨力高、精度可靠等优点。双镜反射法是一种二维角度测量方法，且通过调整激光反射周期数，可以灵活地调整角度测量精度和测量范围。研制的二维偏转角度测量装置采用大尺寸、高精度的融石英玻璃反射镜，具有更大的操作空间，且降低了环境温度对测量精度的影响[4]，测角精度提升到0.1″；采用大幅面、高分辨率的CMOS图像传感器作为激光光斑位置探测器，与二维位置敏感器[5](Position Sensitive Detector, PSD)相比，具有更高的激光光斑位置定位精度，适用于静态或低频动态角度的测量。

文中论述了双镜反射法的计算原理，介绍了测量装置的构成，并提出了一种评价基于双镜反射法测角装置的测角不确定度的方法。

1 设计思路

采用双平面镜激光多次反射实现微小角度高精度测量的设计思路如图1所示，其光路原理是：以基准镜表面为测量基准面，其与激光出射光轴交点为原点建立坐标系，探测器表面与基准镜表面位于同一平面；待测镜与被测物体固定，运动姿态与被测物体同步，待测镜平面和基准镜平面间隔为H；激光相对基准镜平面以θ角出射，照射待测镜后反射回基准镜，此为一个反射周期。经过多个反射周期后，激光光束投射到与基准镜相邻的探测器表面上；当待测镜随被测物体偏转一个小角度α时，激光光束经待测镜一次反射后，反射光线相对入射光线夹角增大2α，第n次反射周期后的反射光线相对入射光线夹角增大2nα，因此激光光束与探测器的交点位置发生改变，求解激光光斑位置变化量相关公式即可得到被测物体的偏转角度。

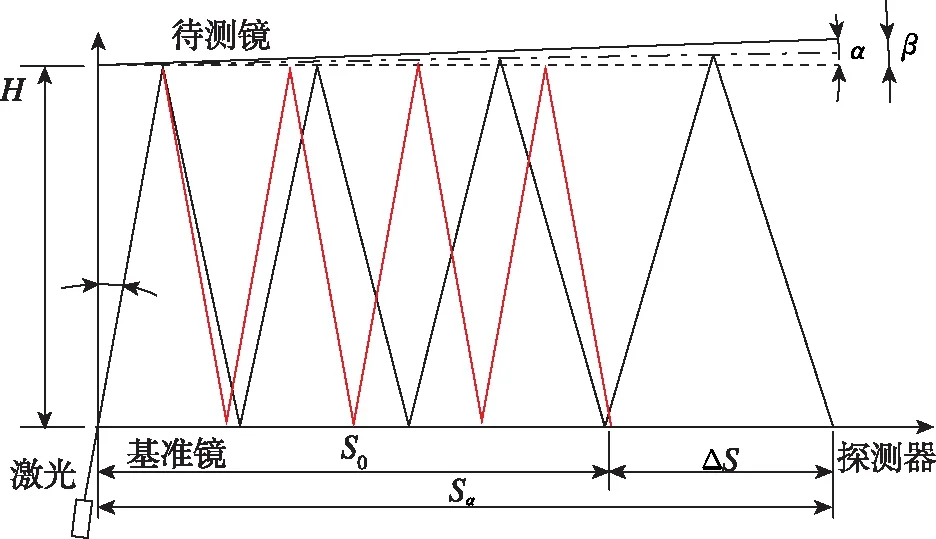
图1 光路原理图Fig.1 Principle diagram of angle magnification by dual mirrors reflections

只考虑一维方向，假设初始状态时待测镜平面和基准镜平面平行，激光光束与基准镜平面的第n个交点到坐标原点的距离S0为：

S0=2nHtanθ

(1)

当待测镜相对初始位置偏转一个微小的角度α，且tanθ较小时，基准镜平面上第n个激光交点到原点的距离Sα可以近似为：

Htan(θ+2nα)

(2)

则相对于初始位置S0，第n个激光交点的位移ΔSα可以近似为：

ΔSα=Sα-S0≈2n2αH

(3)

即激光交点的位移ΔSα与两镜间距H成正比，与待测镜的偏转角度α成正比，与反射周期数n的平方成正比。

则n次反射周期相对1次反射周期的光点位移量的放大倍率η为：

(4)

从式中可以看出，激光光束与基准镜平面交点的位移量与反射周期数的平方成正比，增加反射周期数可以显著提高测角的灵敏度。

当待测镜相对初始位置偏转另一微小角度β时，基准镜平面上第n个激光交点的位移ΔSβ可以近似为：

ΔSβ=Sβ-S0≈2n2βH

(5)

则偏角为β时的激光光点相对于偏角α时的激光光点的位移为：

ΔSβ-α=Sβ-Sα≈2n2(β-α)H

(6)

从公式(6)中可以得出结论：当待测镜偏转角度很小时，激光光束和基准镜平面交点的位移量与待测镜的偏转角度近似成正比，并不要求待测镜平面和基准镜平面的初始状态为平行。但两镜近似平行有助于减小多次反射时激光光束与待测镜平面交点到基准镜平面的距离H值的变化量，降低误差。

正交方向上的激光光束与基准镜平面交点的位移量同理可以计算：

(7)

其中，υ和ω分别表示正交方向上，待测镜偏转前后与基准镜平面之间的夹角。

2 光学模型的建立

根据使用需求，利用光学设计软件ZEMAX建立了仿真光学模型，光路图如图2所示。

图2 光路仿真Fig.2 Optical path layout of dual mirrors reflections

待测镜平面的尺寸为150mm*40mm，基准镜平面的尺寸为100mm*40mm，探测器平面的尺寸为23.04mm*23.04mm。根据一种给定的测试条件，两镜之间的距离为H=1m。反射周期数n=5，则激光光束的投射距离为10m。激光光束与基准镜平面的夹角θ=0.7133°，则第5次反射周期后，激光光束与基准镜平面的交点到原点的距离为124.49936mm。调整激光光束汇聚角度，在探测器上获得较小的激光光斑，便于图像处理时确定光斑中心的位置坐标。

当待测镜偏转一个微小的角度α=0.1″时，激光光斑的位移为ΔSα=24.24μm。因此，选择测量能力优于该位移值的光点位置探测器，即可保证0.1″的角度测量精度。

根据探测器的尺寸，可以很容易地计算出反射周期数n=5时，测角范围约为95″。此时，两镜有效反射区域的间距H的最大变化量约为0.046mm，相对于H=1m，即由与待测镜偏角引起两镜间距H变化造成的测量误差最大仅为0.0046%，可以忽略不计。

表1给出了上述参数条件下，0.1″偏角对应的激光光斑位移值和测角范围与反射周期数的关系。

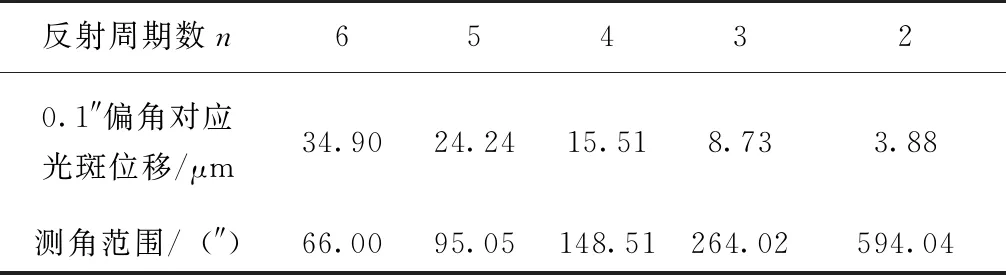
表1 光斑位移和测角范围与反射周期数的关系Tab.1 Relation between reflection cycles and laser spot shifting, angle measurement range

从表中可以看出，对应相同的0.1″偏角，反射周期数越多，光斑的位移越大，即具有更高的角分辨能力，但相应的，角度测量范围也越小。此外，根据之前的分析，增大两镜间距H可以增大激光光束与基准镜平面交点的位移，但在反射镜尺寸的限制下，增大间距可能会减少反射次数，反而造成测量精度的下降，因此减小两镜间距增加反射次数更有利于提高测角精度。

3 试验及结果分析

3.1 试验结果

根据第2节描述的光学模型进行了试验装置的研制，装置实物如图3所示，分为待测镜模块和基准镜模块两个部分。基准镜模块可以实现激光光束的发射和接收，输出激光光斑图像；测镜模块与被测物体固定，体现被测物体的运动姿态。在测量时，基准镜模块安装在二维角度调整台上，根据镜面上激光光斑的位置分布调整基准镜的俯仰和偏摆角度，使其与待测镜平行。基于公式(6)可知，激光光斑的位移量与待测镜的偏转角度近似成正比，并不要求待测镜平面和基准镜平面严格平行，即微小的角度偏差不会影响测角精度。

图3 双镜反射法角度测量装置实物图Fig.3 Picture of instrument of angle measurement by dual mirrors reflections

测量装置采用20mW半导体激光器作为光源，滤波后经激光物镜汇聚出射。滤波孔径小于激光物镜的艾里斑，出射波前可以近似看作理想波面，聚焦在探测器表面时可以获得良好的光斑质量。

采用一种高分辨率CMOS图像传感器作为激光光斑位置探测器，主要参数有：像素分辨率5120*5120，像素尺寸4.5μm*4.5μm，探测器有效尺寸为23.04mm*23.04mm。对于第2节给出的仿真结果，待测镜偏转0.1″时，激光光斑位移为24.24μm，即位移了约5.387个像素，单像素对应的偏角约为0.0186″，通过亚像素插值算法，可以进一步提高偏角测量的灵敏度。

与PSD相比，选用的CMOS图像传感器具有更高的光斑位置定位精度，但帧率只有40fps，即最高只能满足40Hz的动态角度测量，因此该探测器适用于静态或低频动态角度的测量。

调整激光功率使探测器接收到的光斑处于过饱和状态，试验表明，动态角度测量时，过饱和形式的光斑分布具有更可靠的质心提取精度，而高斯形态分布的光斑更适用于静态角度的测量。实测的激光光斑图像如图4(a)所示，光斑约占257.7个像素，直径约为1.16mm，受过饱和影响略大于1.13mm的艾里斑直径。通过图像处理，获得的激光光斑质心坐标如图4(b)所示。

(a)激光光斑

(b)激光光斑质心坐标获取图4 激光光斑及质心坐标获取Fig.4 Laser spot and centroid coordinate extraction

质心坐标获取的图像处理流程如图5所示。通过图像算法，可以实现亚像素级的质心坐标位置提取，光斑质心位置的不确定度优于0.1像素。

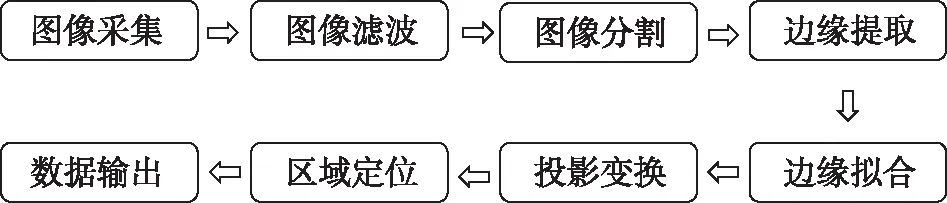
图5 图像处理流程Fig.5 Image processing of laser spot centroid

3.2 结果分析

通常，测量装置的精度需要采用符合计量标准的校准方法或设备进行标定。在标定之前，一般需要保证测量装置的线性度和重复精度等性能指标达到一定的精度等级，以便于根据标定结果进行补偿或修正，使调整后的测量数据具有相应的准确度。因此，通过适当的技术或方法，验证测量装置的不确定度是评价测量装置具备标定可行性的前提。

对于研制的基于双镜反射法的微小角度测量装置，理想的检测状态是给定一个标准的角度值，根据对该角度的实测结果进行精度评价，但具有高置信度的优于0.1″的微小角度较难获取，即很难确定待测镜的真实偏转角度，因此在计量标定之前，通过某种方法验证双镜反射法测角装置的不确定度更具实际意义。

分析公式(2)，基准镜平面上第n个激光交点到原点的距离Sα不仅与待测镜的偏角α有关，还与激光光束与基准镜平面的出射角θ有关，通过调整出射角θ也可以获得激光光斑在探测器表面的位移，从而验证光斑位移与出射角θ之间的线性关系以及不确定度。虽然此验证不能直接反映待测镜偏角α的作用，但硬件性能一致，且光路结构具有相似性，通过分析出射角θ与光斑位移的关系对评价待测镜偏角α的作用具有一定的参考价值。当激光物镜确定后，根据物象关系可以容易地建立出射角θ与激光点源垂轴高度的线性关系，即分析激光点源和激光光斑的相对位移即可表征测角装置的不确定度，通过实验，获得的此项数据如表2所示。

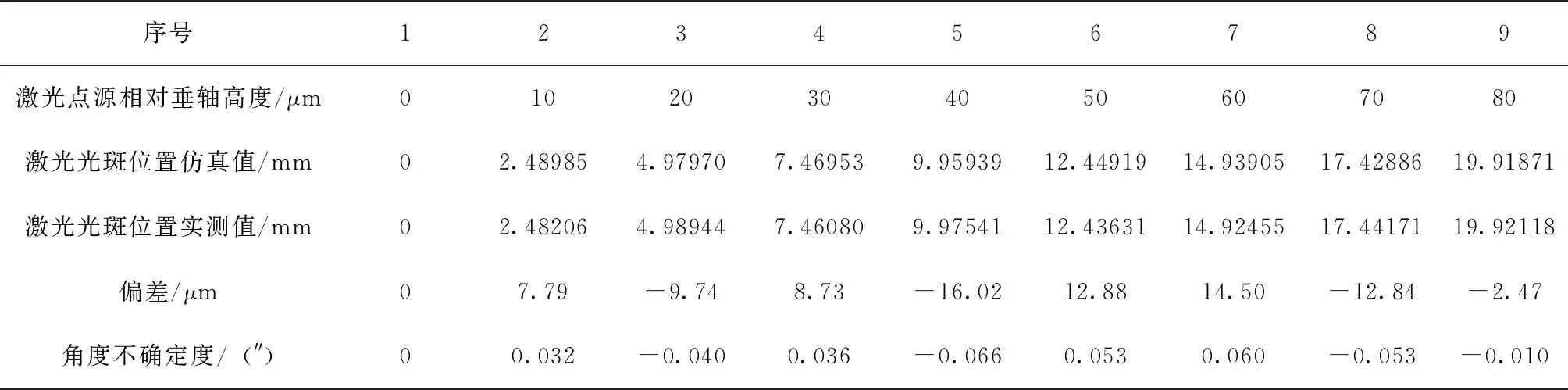
表2 激光点源和激光光斑的相对位移关系Tab.2 Relation between relative displacement of laser source and laser imaging spot

从表格所列的数据中可以看出，受制造精度影响，测量精度相对理论值有所下降，最大角度不确定度为0.06″，但仍能满足0.1″的设计需求。虽然该评价方法并非直接反映待测镜的偏角测量精度，但仍具有一定的参考价值。

4 结 论

论文介绍了双镜反射法测量小角度的原理，根据使用需求进行了光学仿真，并研制了试验装置，验证了该方法的可行性。基于双镜反射法的小角度测量方法和装置能够实现亚角秒级的测角精度，具有分辨率高、精度可靠、结构简单的优点，选用高分辨率CMOS图像传感器作为激光光斑位置探测器适用于静态或低频动态角度的高精度测量。双镜反射法是一种直接测量角度变化的方法，对被测物体的微小平移不敏感，影响该方法测量精度的因素主要有双平面镜的面形精度和空气扰动两个方面。双平面镜的面形精度可以通过先进的光学制造工艺和检测手段保证；在使用该方法进行微小角度测量时，应避免剧烈的空气扰动。