一种正负刚度并联低频隔振器的刚度和动力学特性分析*

刘彦琦，王好奎，黄庭轩，曹东兴

(1.北京市劳动保护科学研究所·北京·100054；2.机械结构非线性振动与强度北京市重点实验室·北京·100124；3.北京工业大学 机械工程与应用电子技术学院·北京·100124;4.上海航天控制技术研究所·上海·201109)

0 引 言

2008年Ibrahim[2]等回顾了非线性被动隔振器的进展情况，详细总结了近年来实现负刚度的典型结构设计方案。对于准零刚度隔振系统的典型设计形式是用一根垂直正刚度弹簧和两根倾斜的对称弹簧来实现的[3-6]。此外，还有其他很多方法，利用欧拉压杆受轴向力屈曲与正刚度弹簧并联的设计方案[7-13]，利用设计滚子球面结构实现负刚度特性并与正刚度并联构成隔振器的设计方案[14-17]，利用水平弹簧和连杆连接并与承载台铰接实现负刚度与正刚度并联的设计方案[18-19]，此外，在减振体上安装动力吸振器同样是一种可靠的减振措施[20-22]。但是目前大多数文献多集中研究分析隔振器的刚度特性，对于阻尼特性没有给予重点考虑。

本文设计一种具有准零刚度特性的非线性低频隔振器，引入非线性阻尼对隔振系统的影响。论文首先分析了系统的刚度和阻尼特性，对隔振带宽进行了优化分析，最后利用谐波平衡法求解隔振器动力学响应，分析了隔振器参数等对振幅放大系数和振动传递率的影响。

1 基于正负刚度并联原理的隔振器设计

图1所示为本文设计的正负刚度并联低频隔振器。其正刚度由一根垂直弹簧提供，刚度为kv，且垂直方向上安装一个阻尼系数为cv的阻尼器；负刚度由4根倾斜对称安装的弹簧提供，刚度值分别为kh，弹簧自由长度为L1，弹簧上端铰接点与下端铰接点竖直方向距离为h，水平方向距离为a；与倾斜弹簧成对安装倾斜阻尼器，阻尼系数为ch，阻尼连杆长度为Lc，阻尼器上端铰接点与下端铰接点垂直方向距离为h。

图1 隔振器原理图Fig.1 The principle diagram of the vibration isolator

1.1 隔振器刚度分析

1.1.1 隔振器的负刚度特性分析

如果仅考虑倾斜弹簧作用，对如图1所示隔振器进行受力分析，系统的弹性力为：

(1)

进行无量纲处理：

(2)

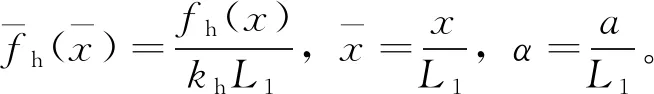
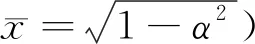
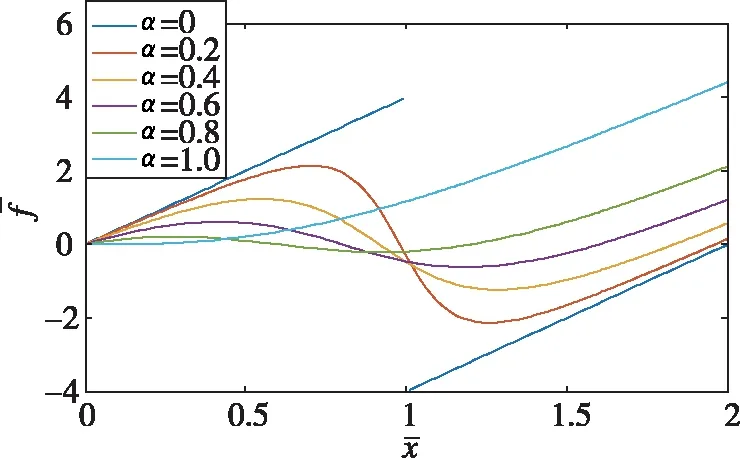
图2 负刚度无量纲弹性力-位移曲线Fig.2 The curve of negative stiffness non-dimensional elastic force - displacement

隔振系统可以承受的最大无量纲力可以通过计算系统的极值得到。由

(3)

可得：

(4)

则可得出系统可以承受的最大无量纲力为：

(5)

由(2)可得，倾斜弹簧的刚度为：

(6)

研究负刚度的刚度位移特性，如图3所示为无量纲倾斜弹簧不同参数α条件下的刚度—位移曲线。根据曲线可知：当α=0时，即初始时倾斜弹簧处于垂直状态，垂直方向上的刚度为一定值；当α=1时，即初始时倾斜弹簧为水平状态，垂直方向上的刚度大于0。当α从0到1逐渐变大时，负刚度的峰值逐渐变小。

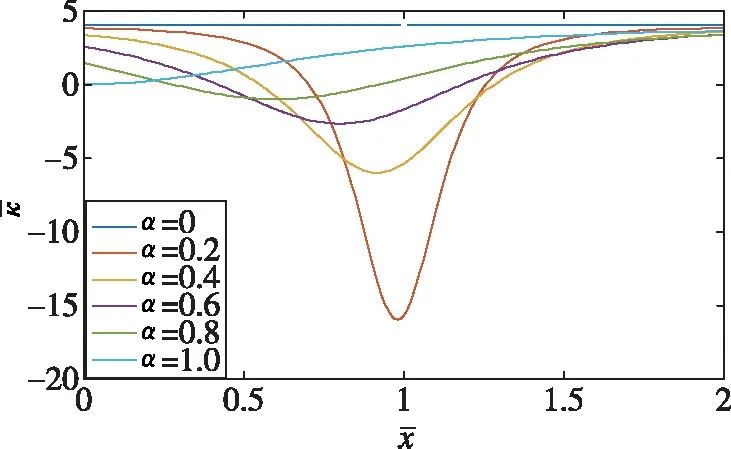
图3 负刚度无量纲刚度-位移曲线Fig.3 The curve of negative stiffness non-dimensional stiffness - displacement

综上，单纯的倾斜弹簧特性曲线呈现非线性，且负刚度系统具有不稳定性。仅依靠负刚度无法实现隔离振动的目的，但是系统的刚度特性的几何非线性和负刚度特性，可以与正刚度元件一起组成隔振系统，使正负刚度并联隔振系统具有高静刚度低动刚度的特性。

1.1.2 正负刚度并联刚度特性

正负刚度并联系统的弹性力为：

(7)

进行坐标转换，令y=x-h，则式(7)变为：

(8)

进行无量纲，得到：

(9)

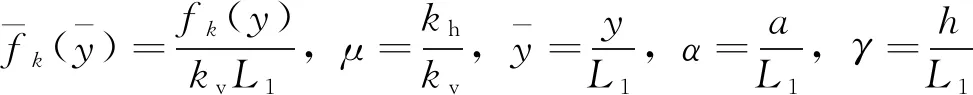
可得出无量纲刚度为：

(10)

(11)

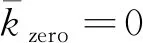
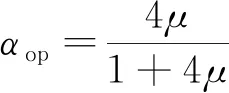
(12)

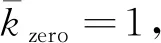
研究正负刚度并联的无量纲刚度特性。如图4所示为μ=0.4条件下正负刚度并联无量纲刚度—位移曲线。由图可以得出：当μ确定后，如果选取的α>αop，则静平衡位置处的刚度值为正；反之如果选取的α<αop，则静平衡位置处的刚度值为负。由于负刚度的不稳定性，在正负刚度并联隔振系统中必须避免出现负刚度。从理论上讲，系统出现零刚度意味着可以隔离的频率范围从0Hz 开始；但是实际中零刚度是很难出现并且几乎不可能出现的(加工、安装的误差都会导致零刚度无法实现甚至会导致系统出现负刚度情况)。

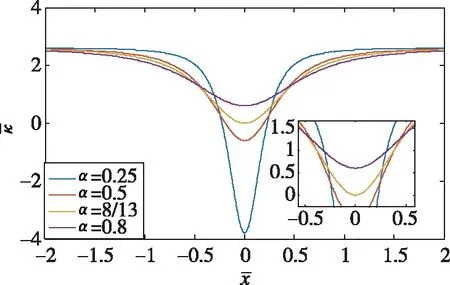
图4 μ=0.4条件下正负刚度并联无量纲刚度-位移曲线Fig.4 The curve of the positive and negative stiffness parallel non-dimensionless stiffness - displacement under the condition of μ=0.4

考虑到实际工程中的加工及装配误差因素，使系统在静平衡位置处接近于0的一个正刚度是最理想的情况，则选取的参数应为α=(1+ε)αop或μ=(1-ε)μop，其中ε为一小量。

设当μ=(1-ε)μop，则μ<μop，

(13)

同理，当α=αop(1+ε)，则a>aop，

(14)

当α=(1+ε)αop或μ=(1-ε)μop时，系统在静平衡位置处的刚度为正且为一个小量，既能满足低频超低频隔振的需求，又可以在工程中实现。

1.2 隔振器参数优化设计

1.2.1 位移隔振带宽优化

为研究正负刚度并联情况下的隔振区域，如图3所示d为隔振器的隔振带宽。由式(10)可求得无量纲隔振位移带宽为：

(15)

将μ=(1-ε)μop代入到上式，则无量纲隔振位移带宽变为：

(16)

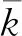
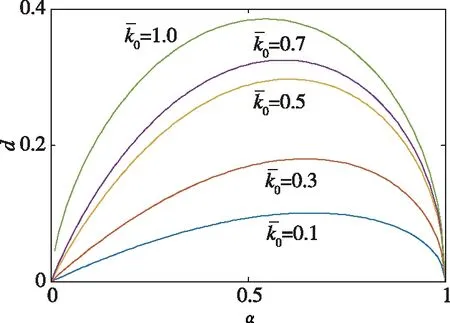
图5 隔振器无量纲隔振位移带宽-初始几何条件曲线Fig.5 The curve of vibration isolator’s non-dimensionless displacement bandwidth - the initial geometry

在工程实际中可以根据隔振需要，及期望隔振系统的无量纲刚度，合理设计参数，使隔振系统具有最大的隔振位移带宽。

1.2.2 斜弹簧数量的影响

由式(10)可知去量纲的两组非线性负刚度组成的系统刚度为：

一组非线性负刚度组成的系统刚度为：

(17)

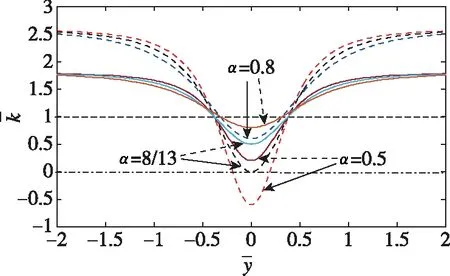
图6 不同数量负刚度情况隔振器无量纲刚度-位移曲线Fig.6 Different number of negative stiffness non-dimensionless stiffness - displacement curve

1.3 隔振器阻尼特性分析

竖直布置阻尼的阻尼力：

(18)

水平布置阻尼的阻尼力：

(19)

设响应为余弦函数y=Ysin(ωt)，则式(18)、(19)可变为：

(20)

(21)

图7 阻尼力-位移无量纲曲线Fig.7 The curve of damping force - displacement

2 动力学特性分析

2.1 建立平衡方程

初始条件：承载质量块m处于静平衡位置(静平衡位置时倾斜弹簧处于水平状态，即y=0)。在外激励为F0cosωt作用下，得出系统的平衡方程如下：

(22)

其中

(23)

且满足条件：mg=kvh

则平衡方程为

(24)

将式中的非线性项用3阶Taylor近似表达：

(25)

(26)

谐波平衡法求解方程，设y(t)=Ycos(ωt+φ)，代入方程(26)中，同次谐波合并，消除高次项：

(27)

存在等式关系：

(28)

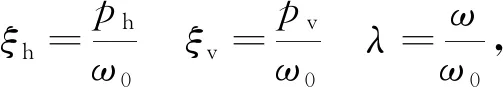
(29)

则可以求得：

Y=

(30)

则无量纲振动响应(振幅放大系数)为

(31)

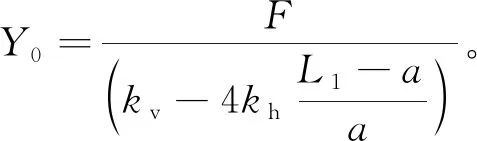
则振幅放大系数为：

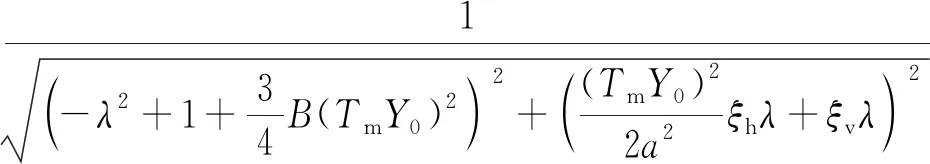
(32)

振动传递给地基的力为：

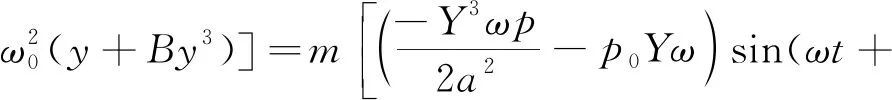
则对应的幅值为：

(33)

可得振动系统力的传递率为：

(34)

2.2 系统解析解正确性验证

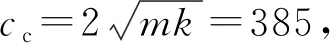
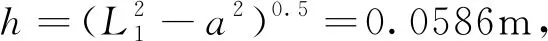
对如上所述参数使用一次谐波平衡法进行近似求解，并为了验证解的正确性，将该解与数值解进行对比，如图8所示，实线部分为采用Rung-Kutta求解的数值解，虚线部分为使用一次谐波平衡法求得的近似解析解，由图可知，二者在稳态部分可以很好地重合，即可以认为谐波平衡法求解的正确性。

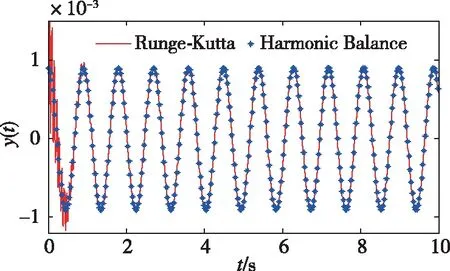
图8 谐波平衡法与Rung-Kutta法响应对比Fig.8 Comparison of harmonic balance method and Rung-Kutta method

2.3 系统参数对振幅放大系数的影响

研究负刚度对振幅放大系数的影响，如图9所示，F0、kv、L1、a不变的条件下，改变水平弹簧的刚度值，即改变隔振系统的负刚度值，从而研究刚度非线性对振幅放大系数的影响。曲线随着水平弹簧刚度值变大向右移动，且曲线的峰值降低。在0<λ<λ1频率段，振幅放大系数Tm随着水平弹簧刚度kh的增大而减小；在λ1<λ<λ2频率段，振幅放大系数Tm按照水平弹簧刚度kh从小到大的顺序分别大于水平弹簧刚度等于0时的Tm值；在λ2<λ<λ3频率段，振幅放大系数Tm随着水平弹簧刚度kh的增大而增大；当λ>λ3频率段，无论水平弹簧刚度kh如何变化，Tm都很小，且都等于水平弹簧刚度kh等于0时的值。即该隔振器增加水平弹簧刚度值有利于减小振动物体响应的峰值。

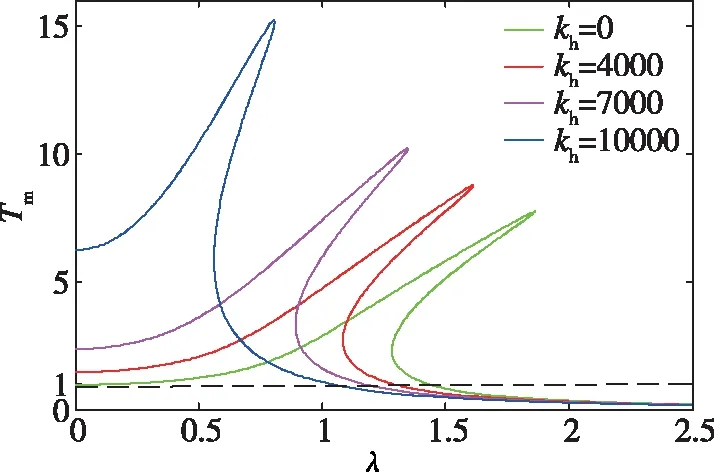
图9 刚度非线性对振幅放大系数影响曲线Fig.9 Influence curve of stiffness nonlinearity on amplitude amplification coefficient

研究非线性阻尼对振幅放大系数的影响，如图10所示，固定其他参数不变条件前提下，改变水平阻尼的阻尼系数，研究不同水平阻尼系数情况下，振幅放大系数的变化曲线。在0<λ<λ1及λ>λ2频率段，无论水平阻尼系数ch如何变化，振幅放大系数Tm的曲线都近似重合，且随着激励的不断增大，振幅放大系数Tm趋近于0；在λ1<λ<λ2频率段，振幅放大系数Tm及其峰值随着水平阻尼ch的增大而减小。即在低频段和高频段，水平阻尼对振幅放大系数影响不大，在中频段，增大水平阻尼会降低振幅放大系数及其峰值。总体而言，增加水平阻尼，对于降低振幅放大系数是有利的。

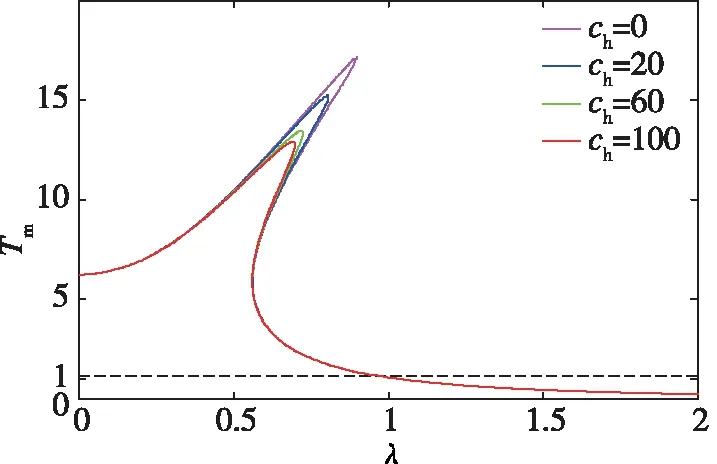
图10 阻尼非线性对振幅放大系数影响曲线Fig.10 Influence curve of damping nonlinearity on amplitude amplification coefficient

研究竖直阻尼对振幅放大系数的影响，如图11所示在固定其他参数条件不变的前提下，改变竖直阻尼的阻尼系数，研究不同竖直阻尼系数情况下，振幅放大系数的变化曲线。曲线随着竖直阻尼的增加向左移动，且峰值降低；在0<λ<λ1频率段，振幅放大系数Tm及其峰值随着数值阻尼的增大而降低；在λ>λ1频率段，不论竖直阻尼如何变化，振幅放大系数曲线近似重合，且随着激励的不断增大，振幅放大系数Tm趋近于0。即增加阻尼的阻尼系数，有利于降低系统的振幅放大系数。

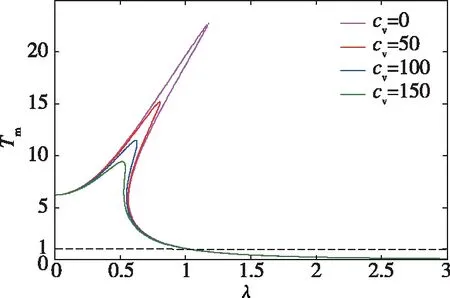
图11 阻尼对振幅放大系数影响曲线Fig.11 Influence curve of damping on amplitude amplification coefficient

对比图10和图11，在相同参数情况下，改变竖直阻尼的阻尼系数相比于改变水平阻尼的阻尼系数，会对系统的振幅放大系数产生更大的影响。

研究激励幅值对振幅放大系数的影响，如图12所示kh、kv、L1、a不变的条件下，改变激励幅值的大小，研究不同的激励幅值情况下，振幅放大系数的变化曲线。振幅放大系数曲线随着激励幅值的增大向右移动，且峰值降低。在0<λ<λ1频率段，振幅放大系数Tm随着激励幅值F0的增大而减小；在λ1<λ<λ2频率段，振幅放大系数Tm按照激励幅值F0从小到大的顺序分别大于激励幅值为30时的Tm值；在λ2<λ<λ3频率段，振幅放大系数Tm随着激励幅值F0的增大而增大；当λ>λ3频率段，无论激励幅值如何变化，Tm都很小，且都接近于0。即对于该隔振器，当系统参数设定后，对于不同的激励幅值有不同的振幅放大系数特性，该隔振器对于较大的幅值激励振幅放大系数更小。

图12 激励幅值对振幅放大系数影响曲线Fig.12 Influence curve of excitation amplitude on amplitude amplification coefficient

综上，增加系统的非线性刚度和非线性阻尼及竖直阻尼，都利于降低系统的振幅放大系数，且在系统的系数都确定的情况下，对于不同的激励幅值，激励幅值越大，系统的振幅放大系数越小。

2.4 系统非线性项对振动传递率的影响

为研究非线性刚度对振动传递率的影响，如图13所示，在固定系统其他参数，改变水平弹簧刚度值，即改变隔振系统的非线性刚度，从而研究非线性刚度对振动传递率的影响。曲线随着水平弹簧刚度的增加向右移动且峰值降低。在0<λ<λ1频率段，振动传递率T随着水平弹簧刚度kh的增大而减小；在λ1<λ<λ2频率段，振动传递率按照水平弹簧刚度kh从小到大的顺序分别大于水平弹簧刚度等于0时的振动传递率T的值；在λ2<λ<λ3频率段，振动传递率T随着水平弹簧刚度kh的增大而增大；当λ>λ3频率段，无论水平弹簧刚度kh如何变化，T都很小，且都等于水平弹簧刚度kh等于0时的振动传递率值。即增加水平弹簧刚度值(增加隔振系统非线性刚度)对于提高系统隔振性能是有利的。

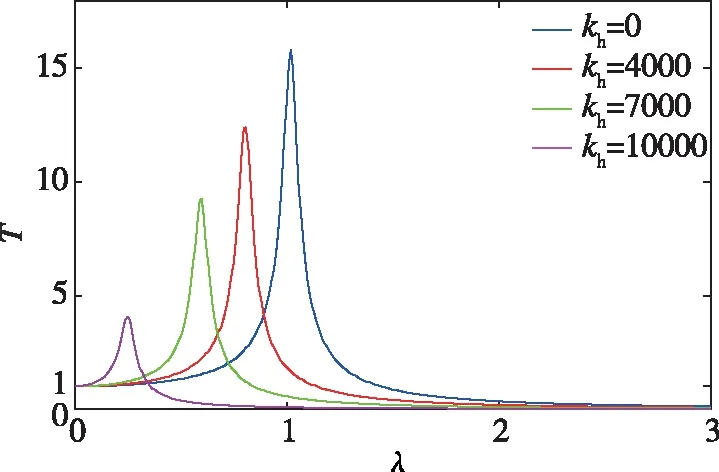
图13 非线性刚度对振动传递率影响曲线Fig.13 Influence curve of nonlinear stiffness on vibration transfer rate

为研究非线性阻尼对振动传递率的影响，如图14所示，固定系统其他参数，改变水平阻尼的阻尼系数ch，即改变非线性阻尼，从而研究非线性阻尼对振动传递率的影响。在0<λ<λ1和λ>λ2频率段，振动传递率曲线不论水平阻尼的阻尼系数如何变化曲线都近似重合，且随着激励频率逐渐增加，振动传递率趋近于0；在频率段λ1<λ<λ2段，振动传递率曲线及其峰值随着水平阻尼的增加降低。即增加水平阻尼对于降低系统的隔振率提高系统的隔振性能是有利的。

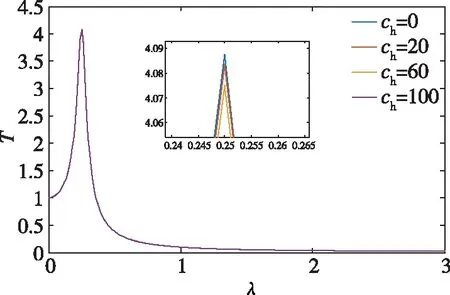
图14 非线性阻尼对振动传递率影响曲线Fig.14 Influence curve of nonlinear damping on vibration transfer rate

综上，增加系统的非线性刚度和非线性阻尼都有利于降低系统隔振传递率，提高系统的隔振性能，虽然阻尼非线性对系统的隔振性能影响不大，但是不能忽略。

3 总 结

本文研究具有非线性刚度和非线性阻尼的一种基于正负刚度并联原理的隔振器，对隔振器的刚度特性和阻尼特性进行分析，并分析其位移隔振带宽，对不同的斜弹簧数量进行对比分析，研究该隔振器的优势及特点；对该隔振器进行了动力学特性分析，建立了系统的平衡方程，利用谐波平衡法求解系统响应及系统的振幅放大系数和力传递率，并进行了数值分析，解析解与数值解进行了对比验证，分析了非线性刚度、非线性阻尼、阻尼特性以及激励幅值等对隔振器振幅放大系数的影响，此外，数值分析了非线性刚度及非线性阻尼对隔振器激振力传递率的影响。研究结果表明，对本文提出的这类正负刚度并联隔振器设计，可以根据激励情况及隔振要求进行隔振器的刚度、阻尼及几何参数的优化设计。