挠性空间结构振动的独立模态空间最优控制方法*

金 珊, 郭延宁，李传江

(哈尔滨工业大学 航天学院·哈尔滨·150001)

0 引 言

随着航天任务需求增多，航天器功能扩展、平台增大，越来越多的航天器都附带挠性结构，且尺寸、规模逐渐增大，结构愈发复杂化。加拿大Radarsat-1卫星的SAR天线的展开长度约15m，太阳帆板的面积约25m2。美国的Lacross合成孔径雷达卫星，太阳能电池阵长达45.1m，最多可提供20kW的能量。2004年发射的Anik-F2卫星，其太阳能单翼长达20m，提供18kW的能量。仍在规划阶段的，如美国国防部ISAT项目中，涉及长度超过300m的展开式桁架结构。诸如此类的航天器在未来航天器中具有显著的发展趋势。

外太空复杂的环境干扰作用，航天器不断进行姿态机动或变轨，而挠性空间结构表现出低频振动、模态密集等非线性动力学特性，与本体强耦合，振动会严重干扰航天器本身的姿轨控制，不仅影响正常载荷任务的进行，更甚者会导致控制失效。改进控制方案，能够提高航天器的姿态跟踪精度、响应速度和系统稳定性，研究如何对大型挠性空间结构进行有效主动振动抑制问题具有实际工程意义。

调研国内外文献发现，对于普通带挠性附件的航天器控制国内外已经进行了大量理论研究和试验验证，取得众多研究成果。被动振动控制是比较容易实现的一类方法，成本较低，通常不需要额外能量，能保证系统稳定性。其主要实现是利用阻尼材料改变系统特性[1-2]，或在挠性结构上额外增加阻尼器等装置[3]。

挠性结构主动振动抑制有两种设计思路，一种是沿袭传统刚体航天器的振动控制，将挠性结构与中心体整合成一个全挠性系统进行控制方法研究[4-7]。胡庆雷等[8]针对挠性航天器大角度姿态机动，提出将输入成形法与变结构控制法相结合的控制方法。另一种是将控制作用直接施加于挠性结构，通过构成独立的闭环反馈控制回路实现振动抑制。Mehiel等[9]对太空可展开望远镜，设计了基于命令追踪发生器的离散自适应控制器。张维存等[10]提出了一种多模型自适应控制算法，一定程度上克服传统算法在被控系统参数跳变时响应品质下降的问题。Ryan等[11]提出递归最小二乘法的自适应参数估计量改进正位置反馈控制。Mahmoodi等[12]利用一阶补偿器提供阻尼控制改进传统正位置反馈控制。陈学前等[13]采用离线神经网络提高控制器的鲁棒性，并给出了一种模态空间最优控制律。王波等[14]对主被控模态独立模态控制，对非主被控模态利用耦合模态控制，降低了系统能耗并提高鲁棒性。李生权等[15]提出了一种基于加速度信号的独立模态空间控制法。李维[16]对压电智能结构定义广义本构关系，设计线性二次型最优反馈控制器。李传江等[17-18]提出一种结合动态补偿思想的双幂次趋近律与终端滑模面的有限时间控制律。由于存在次生模态、参数跳变时控制品质下降等问题，仍存在进一步研究的必要性。针对挠性结构各阶模态在实模态空间下具有耦合特性，将控制问题转化到独立模态空间中进行分析，并基于最优理论设计控制器进行仿真验证。

1 挠性空间结构有限元模型与模型降阶

一般地，多自由度系统动力学方程式可表示为

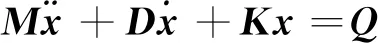
(1)

其中，x为物理空间的结构位移，M、D、K分别为系统n*n阶的质量矩阵、阻尼矩阵和刚度矩阵，Q为节点载荷力。空间结构可以抽象简化为杆等结构单元的组合，集成可得到整体结构的质量矩阵和刚度矩阵。由动力学问题的有限元分析方法[19]和上式，系统的特性矩阵有

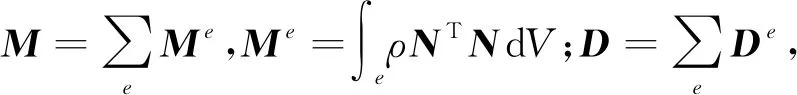
(2)

ρ为系统的材料密度，μ为系统阻尼比，N为位移的插值函数，Σ为应变量矩阵[20]。

对于这类分布参数的结构，仍采用偏微分方程描述其运动形式，从而建立常微分方程表达的控制模型。

(3)

其中，Dp为阻尼系数，B为n*r作动器安装位置矩阵，f为r*1控制力向量，r为作动器安装个数。y为m*1测量向量，m为传感器安装个数；Cd、Cv为输出系数矩阵，分别代表位移和速度传感器；D为作动力直接输出系数。

系统响应按模态叠加可表示为

(4)

其中，φi为第i阶振型，φ=[φ1,φ2,…φi]；ηi为第i阶模态坐标，η=[η1,η2,…ηi]T

式(4)代入式(3)得

(5)

其中DΓ=diag(2ξ1ω1,2ξ2ω2,…，2ξnωn)，ξi,ωi,i=1,2,…，n为系统固有模态阻尼比及频率。

系统模态叠加的状态方程为

(6)

式中PN为系统的状态响应向量。N=1,2,…,n为截断阶数。

在线性空间中定义能量范数

(7)

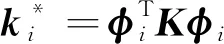
进一步，定义系统能量判据

(8)

取不同的模态截断阶数，计算式(8)，得到曲线如图1所示，当模态阶数超过10以后，曲线变化趋于平缓，因此选择前10阶模态进行计算来近似代替整体结构的振动状态。

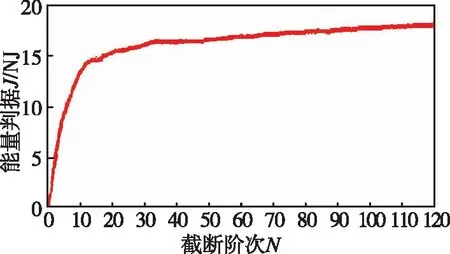
图1 能量判据与模态截断阶数关系曲线Fig.1 Energy criterion and modal truncation order curve

2 基于独立模态空间理论的控制器设计

根据系统响应(5)，可得其在实模态空间的表达式：

(9)

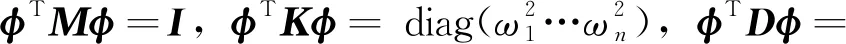
转换成关于模态状态向量z的状态方程：

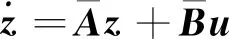
(10)

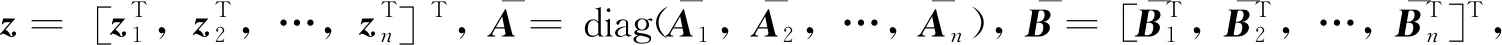
i=1,2,…,n

由模态正交归一化条件，得到从物理空间到模态空间的状态解耦为

(11)

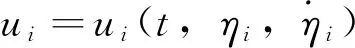
(12)

则闭环系统的模态方程为

(13)

可确定实际控制力为

u=φTBf=Γf

(14)

2.1 系统频率响应的模态滤波器设计

由振型的叠加原理如式(5)，又由于模态具有正交性和归一性，状态解耦后的模态空间方程可以表示为

η=φTMp=ΨTδ

(15)

其中nt为测量点数。ΨT=φTM为模态滤波器解耦矩阵。

定义系统在第t自由度下激励的频率响应函数为

(16)

对于一个特定的输入频率，频率响应函数可简化为

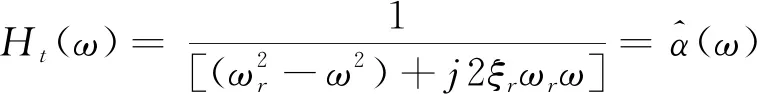
(17)

2.2 模态参数获取的Luenberger观测器设计

状态空间中系统的被控模态用状态方程表示为

(18)

为系统引入Luenberger观测器，观测器的形式为

(19)

其中Kr为观测器的增益矩阵。

模态控制力可表示为

(20)

令Vr=(Ir+KrCr)-1，其中Ir为单位矩阵，则有

(21)

观测器的误差为

(22)

2.3 基于最优理论的独立模态空间控制器设计

设第i阶模态的控制力向量为fi=gi1ηi+gi2ηi,i=1,2,…,n，其中gi1、gi2为控制器的增益系数。

建立最优控制的性能指标函数为

(23)

Ri用于平衡系统能量和外界输入能量，将控制力向量的线性反馈代入性能指标函数，并使Si最小，可以解得控制器增益为

Ri+2Riωia)1/2

(24)

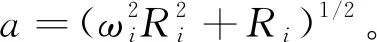
存在可测的外界扰动λ时，第i阶模态状态空间方程可写成

(25)

模态控制力为

(26)

求取合适的Gi使状态反馈满足系统渐近稳定[21]，系统的第i阶传递函数‖Ci(sI-Ai-Bi1Gi)-1Bi2‖∞<γ，且Ai+Bi1Gi渐近稳定，其中γ为一正常数。根据H∞次优控制方法可知存在ε>0和正定矩阵Q，使以下代数Ricatti方程存在正定解Pi

(27)

求解上述方程组得

2+2(1+a)1/2)1/2)-1]

(28)

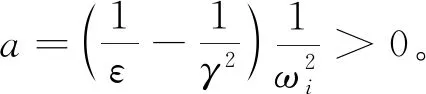
系统控制增益系数为

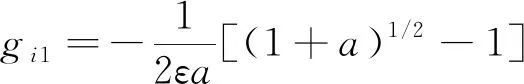
(29)

3 挠性空间结构振动控制仿真分析

3.1 仿真模型

以桁架结构和一组帆板结构为例(如图2所示)给出相关挠性空间结构的部分主要参数如表1所示。截取前10阶模态参数，只对前3阶进行控制，分别在中心体保持静止和不同转动和干扰工况下进行主动振动控制。

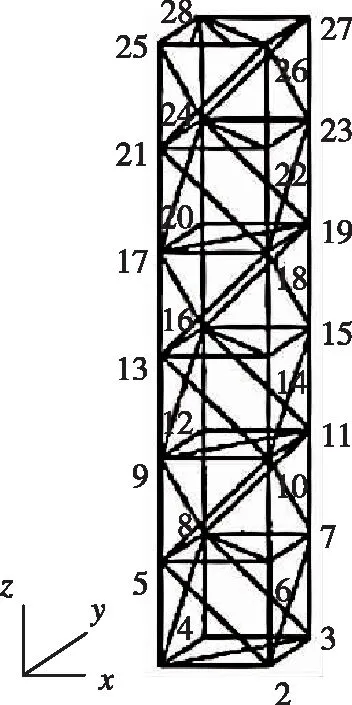
(a) 桁架节点编号示意图

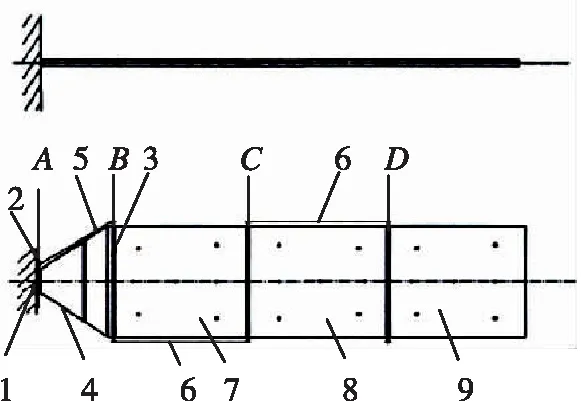
(b) 帆板结构示意图图2 仿真挠性空间结构示意图Fig.2 Schematic diagram of the flexible space structures

表1 被控大型挠性空间结构模型部分参数Tab.1 Partial parameters of the controlled large flexible space structure model

3.2 结果分析

参考作动器配置的计算结果，采用1、2阶布置5个作动器，3阶布置2个作动器。从图3中可以看出能够有效地进行主动振动抑制。如图3中虚线所示，桁架结构的振动在自然状态下衰减得很慢，施加控制后结构的振动很快衰减。各方向的位移衰减超过97%，同时各阶作动器的作用时间均小于150s。将控制器增益换成H∞次优控制律，控制效果类似。

对于单翼帆板结构，假设航天器中心体从初始位置姿态[0.5,-0.5,0.5]°、初始角速度[-0.01,0.02,-0.03] (°)/s开始，调整中心体附带天线以固定角速度绕-Y轴、+X轴旋转，到目标姿态，在此过程中考虑挠性空间结构的振动情况并进行主动振动控制。采用比例积分微分(Proportional Integral Differentiation, PID)控制器进行控制效果对比。图4给出前5阶模态坐标变化和被控对象三轴振动耦合力矩变化。

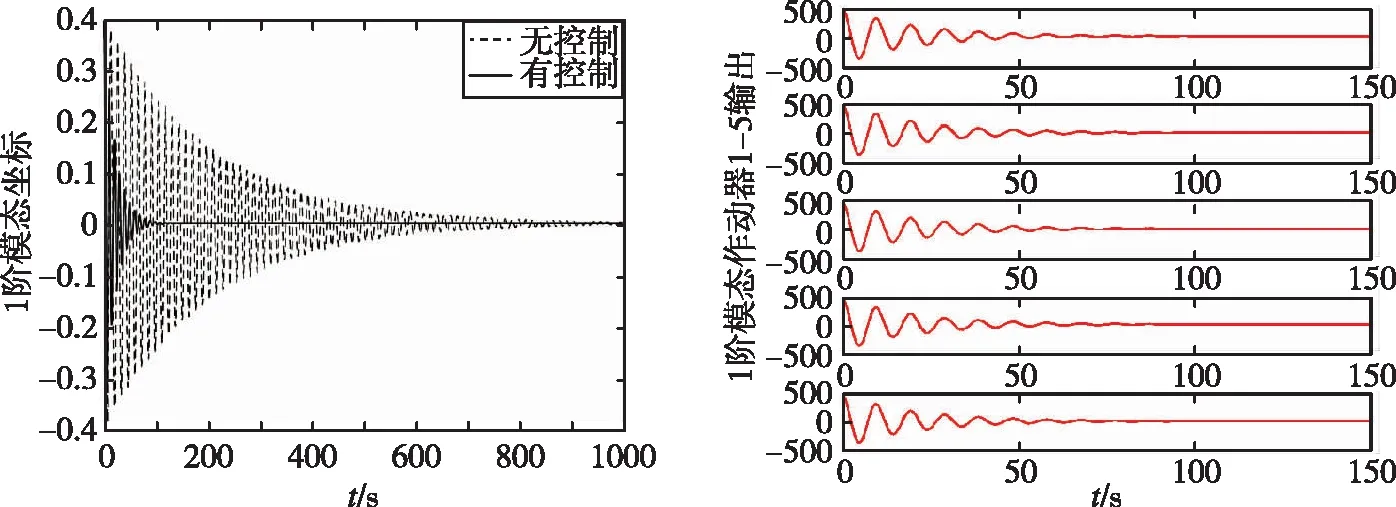
(a)1阶模态振动和作动器输出

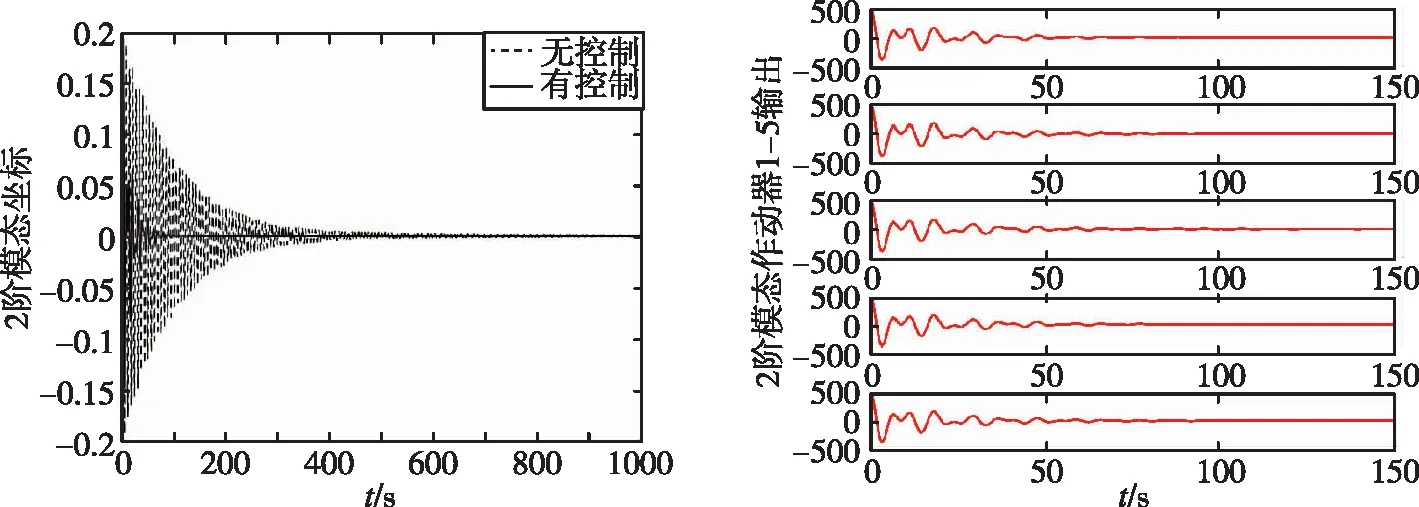
(b)2阶模态振动和作动器输出

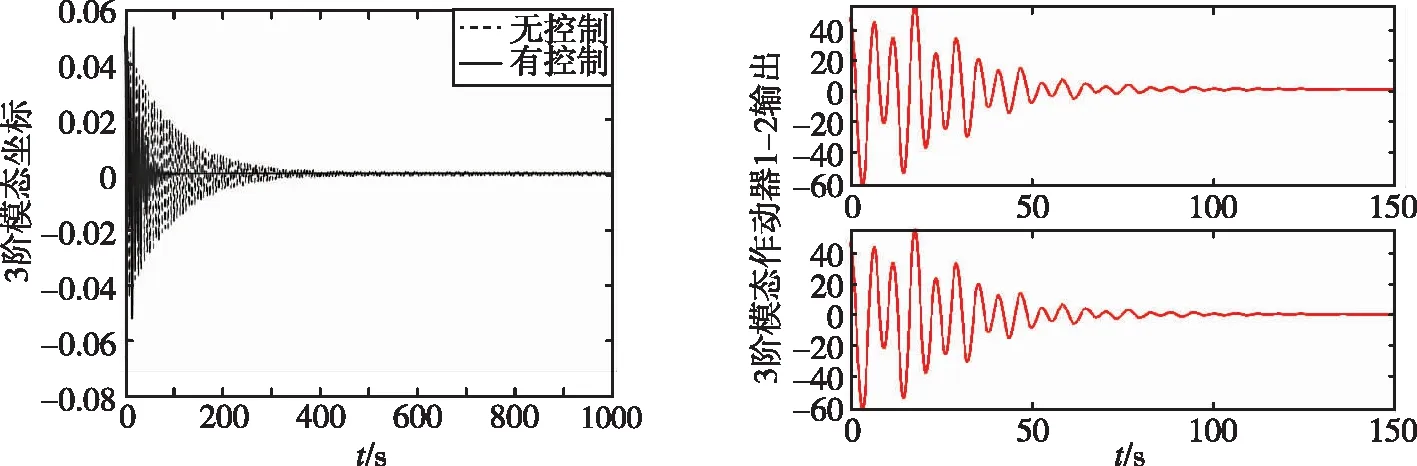
(c)3阶模态振动和作动器输出图3 前3阶模态曲线和作动器输出Fig.3 1-3 order modal curve and actuator output

如图4所示，作动器的输出对1阶模态的控制溢出影响较大，与PID控制器相比，第1阶模态振动的衰减程度较小，最优独立模态空间控制(Independent Modal Space Control, IMSC)控制器最大振幅约为后者的70%，H∞次优IMSC控制器最大振幅约为PID的57%，而2～5阶模态振动的衰减程度明显减小，系统的振动抑制能力增强，三轴耦合力矩的大小有所减弱。

(a)PID方法

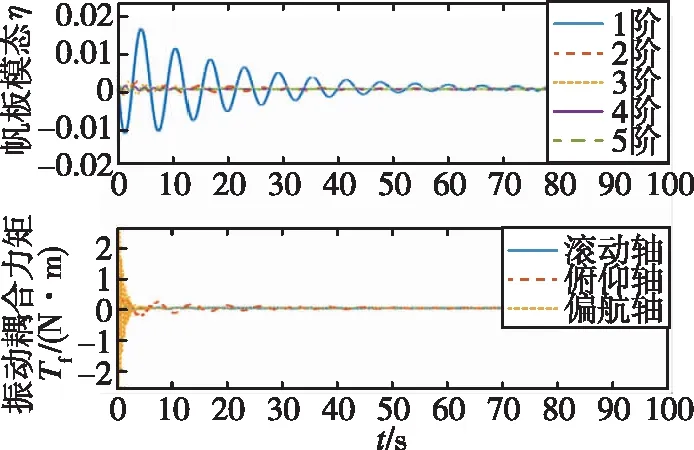
(b)最优IMSC方法

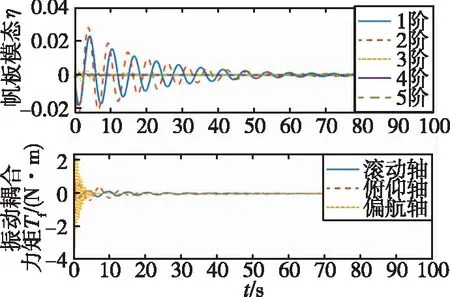
(c)PID方法

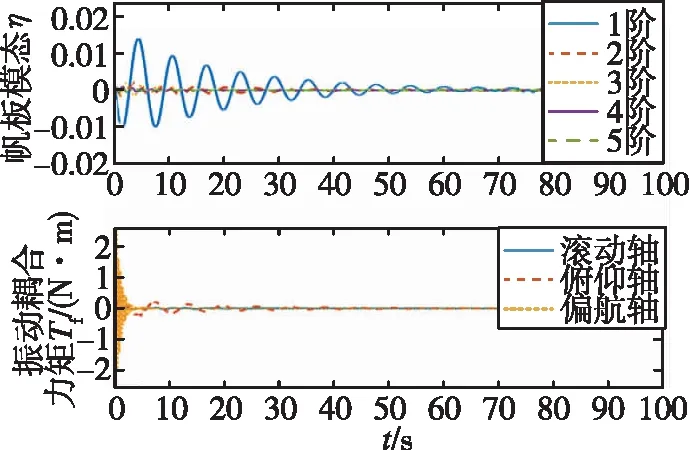
(d)H∞次优IMSC方法图4 帆板结构主动振动控制仿真曲线Fig.4 Simulation curve of active vibration control of panel

在中心体调整稳定过程中，在15s时外加幅值为0.1的脉冲干扰，振动控制曲线如图5所示，均会在10s内产生一个较大的振幅，最优控制IMSC方法下模态坐标的最大振幅约0.23，H∞次优IMSC方法下模态坐标的最大振幅约为0.15，较前者小约35%。这是由于H∞次优独立模态空间控制律的设计中包括了外力干扰项，控制律的作用更有针对性，在抑制外力引起的干扰时，系统具有更好的抗扰性能。

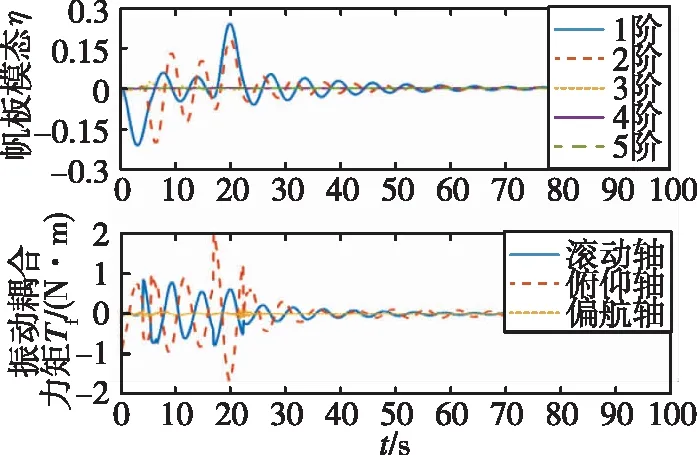
(a)最优IMSC方法

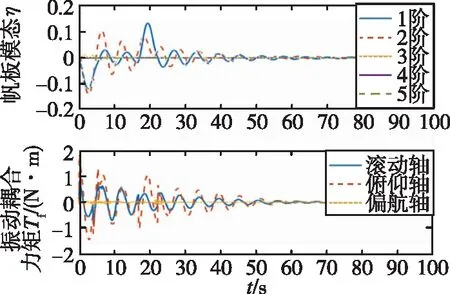
(b)H∞次优IMSC方法图5 脉冲干扰下帆板结构IMSC方法振动控制仿真曲线Fig.5 Simulation of panel IMSC vibration control under pulse interference

4 结 论

本文研究了大型挠性空间结构的有限元分析与建模、主动振动控制，采用简化的空间挠性附件，如桁架和帆板等为仿真模型算例，验证了基于独立模态空间控制理论的控制律，对中心体机动工况和受到外部干扰激励下，挠性结构的振动模态进行了主动控制。但本文未考虑溢出问题和密集模态的影响，因此在后续研究中应考虑观测溢出、控制溢出和低频模态密集分布的控制问题。