一种新型的挠性航天器作动器布局优化方案*

郭延宁，王鹏宇，金 珊

(哈尔滨工业大学 航天学院· 哈尔滨·150001)

0 引 言

近年来，随着航天技术的不断发展，航天器的规模不再受一次发射条件的限制，大尺度挠性航天器因此进入了人们的视野。例如，苏联在20世纪80年代发射的“和平”号空间站，长13.1m，质量为21t，其侧面还装有多个挠性太阳能帆板[1]。除大型空间站外，一些用于深空探测、对地成像、目标跟踪的新型航天器也装配有大规模挠性附件或挠性舱段。例如，日本的工程试验航天器ETS-VIII[2]、美国的“Mars Geoscience/Climatology Orbiter”火星探测器[3-4]，都采用了大规模的外展式桁架结构，用于实现天地通信或电磁隔离。这些大型附件一般具有刚度低、阻尼小、振动频率密集等特点，且其挠性振动与航天器本体姿态运动之间往往存在较大耦合，如果不对其进行有效振动抑制，将导致航天器失稳等严重后果。因此，研究大挠性航天器的振动抑制问题，具有重要的工程意义。

对于挠性航天器的振动抑制问题，已有大量学术成果，主要方法可分为被动振动抑制和主动振动抑制[4]。其中，被动振动抑制是通过对挠性部件进行结构设计，实现对振动的耗散、阻尼或隔离。该方法存在着精度低、鲁棒性差等缺陷，往往难以满足现代航天任务的高精度需求[5]。主动振动控制通过安装在挠性附件上的作动器，能够实现对挠性附件的高精度控制；且其控制回路与航天器姿态系统分离，便于控制规律设计和系统稳定性分析[6]。在采用主动振动抑制时，振动作动器的位置直接决定了系统对挠性振动的抑制能力，而如何对作动器进行合理配置，仍是目前需要深入研究的问题。

对于作动器布局方法的研究主要从两个方面展开，一是根据实际需求，设计作动器安装位置的优化指标或约束条件；二是改进优化算法，提升优化速度[7]。对于优化指标设计问题，目前已经形成了一套较为完备的理论体系，本文对工程中常用的优化指标归纳如下：

(1)考虑系统能量的优化指标：从能量耗散的角度出发，重点研究弹性势能衰减与作动器输出控制力之间的数学关系，在实现对挠性结构振动抑制的同时减少作动器的控制力[8-10]。基于系统弹性势能，李俊宝等通过引入能量耗散因子描述了系统弹性势能的衰减速率，构建了相应的优化指标，进而实现了作动器的优化配置[8]。类似地，顾荣荣等从有效衰减能量出发，根据Lyapunov第二法定义了目标函数并对作动器安装位置进行了设计[9]。

(2)考虑系统可控的优化指标：在对系统进行控制律设计之前，首先要保证系统状态是可控的，因此用于描述系统状态受控程度的概念应运而生，即系统可控度。Hamdan等基于二阶微分方程，基于响应系数矩阵给出了系统可控度的计算方法，为作动器的配置带来了方便[11]。在此基础上，李东旭等重新定义了振动控制系统可控度的概念，将作动器的控制电压引入到系统设计中来并建立了更为实用的优化准则[12]。

(3)考虑失效和可靠性的优化指标：对在轨运行的航天器进行维修成本高昂且存在很多技术难题，因此考虑作动器故障的安装位置优化指标具有重要的工程价值。Matunaga等[13]从容错系统设计的角度出发，分析了作动器失效的各种形式，建立了相应的数学模型，为容错优化指标的建立和考虑可靠性的作动器优化配置提供了理论基础[14]。

上述优化指标均从理论角度出发，分别对振动控制系统的能耗、可控度、容错性进行优化，然而为作动器供电的电缆所引发的能量损耗及电磁干扰并未考虑其中。此外，大型挠性航天器具有模态频率低且密集的特点，高阶模态振动对航天器姿态控制的影响不能忽略，在设计作动器安装位置时，需先保证系统对各阶模态都具一定的控制能力。综上，本文针对振动作动器优化布局问题，提出考虑系统状态可控度及作动器电缆长度的复合优化指标，并根据该指标采用遗传算法对作动器安装位置进行寻优，在保证系统可控度的同时，减小作动器供电电缆长度，进而减少系统的能耗和电磁干扰。

1 数学模型的建立

本文利用有限元法建立挠性航天器的振动控制模型。假设航天器挠性部件上的有限元节点数目为n，安装作动器的数目为nc，且所有作动器均跨接在两个相邻的有限元节点上。在有限元模型中，认为各节点之间由无质量的弹簧链接，进而通过数学分析建立各节点之间的力学关系和运动约束。作动器嵌入桁架后，可认为作动器只对其跨接的两个节点有力的作用；而对其他节点的作用力则是有限元模型的内力，由无质量弹簧进行传递。如图 1所示，若作动器沿着节点编号m→n方向安装，其与本体系三轴方向的夹角分别为α、β、γ，则作动器安装方向在本体系下的方向余弦为cosα、cosβ、cosγ。

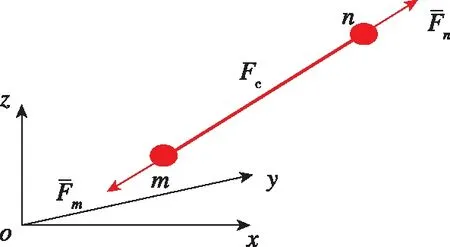
图1 有限元节点受力分析图Fig. 1 Force analysis for a finite element

当作动器产生幅值为Fc的控制力时，节点n受力为

(1)

节点m受力为

(2)

则作动器为整个挠性结构提供的控制力为

(3)

考虑航天器刚挠耦合特性及环境干扰，航天器上所有挠性部件的振动控制规律，均可采用如下数学模型进行描述[15]

(4)

其中，M∈Rn*n、C∈Rn*n、K∈Rn*n分别为系统的质量、阻尼、刚度矩阵；ω∈R3*1为航天器姿态角速度在本体系下的投影；L∈Rn*3是航天器姿态运动与挠性结构各有限元节点振动的耦合系数；δ为挠性附件上有限元节点的位移矩阵；fd∈Rn*1、fa∈Rnc*1分别代表干扰力列向量和作动器输出的控制力列向量；B∈Rn*nc为振动作动器的安装位置矩阵，由作动器的方向余弦组成。

为了便于控制系统设计，还需要将振动控制方程式(1)转换至模态空间下，并进行适当的模态截断。定义系统的振型矩阵为U∈Rn*n，则根据振动理论可知

δ=Uη

(5)

其中，η为挠性部件的振动模态坐标。考虑对上式进行模态截断，则有

δ=Uaηa

(6)

其中，Ua是系统前na阶振动的振型矩阵，ηa为截断后的振动模态坐标。

进一步，可得模态空间下的系统振动控制方程，具体形式为[15]

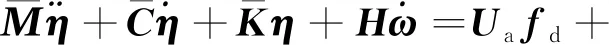
(7)

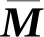
2 基于遗传算法的作动器布局优化方案

2.1 考虑作动器电缆长度的复合优化指标

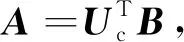
VTAcV=uTu

(8)

其中，Ac=ATA是一个nc*nc阶正定矩阵。

根据式(8)，可得如下不等式

(9)

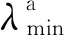
(10)

则可建立如下的作动器安装位置优化指标：

(11)

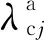
如前所述，作动器电缆越长其能量损耗越大，且更容易对航天器的高精度载荷产生电磁干扰。因此，缩短作动器电缆长度可以有效减小系统能量损耗及电磁干扰，提高振动控制系统的可靠性。综上，将式(11)中的优化指标改写为

(12)

其中，X为作动器安装位置向量；μ为加权系数，μ越大则作动器电缆长度在优化指标中所占权重越大。该加权优化指标兼顾了系统可控度和作动器电缆长度，在保证系统可控的前提下，能够有效缩短作动器电缆长度。

2.2 遗传算法优化

遗传算法采用了达尔文进化论中优胜劣汰的思想，利用复制、交叉、变异等操作来模拟自然进化过程，完成对复合性能指标的最优个体的全局搜索，具有优化速度快、干扰鲁棒性强等优势[11]，其操作流程如图2所示。

图2 遗传算法操作流程图Fig. 2 Flow chart of the genetic algorithm

(1)编码与解码

本文利用二进制字符串对作动器的所有可选安装位置进行编码，二进制字符串长度与可选安装位置总数相等。具体操作规则为：安装作动器的位置二进制编码设置为1；未安装作动器的位置相应二进制编码设置为0。例如，在某个挠性部件上预先选定了10个位置作为可选安装位置，在编号为3、5、7的位置上安装作动器，则对应的二进制编码为[0 0 1 0 1 0 1 0 0 0]。

(2)适应度比例选择操作

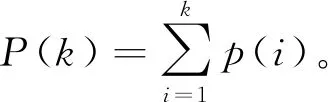
(3)交叉操作

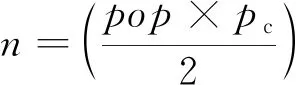
(4)变异操作

设变异概率为pm，对于每一位基因都产生一个[0,1]之间的随机数c，用于判断变异是否发生，若c≤pm则对该编码进行变异操作，即由0置1或由1置0。变异操作能够为种群不断引入新的个体，提高遗传算法的全局搜索能力，有效避免搜索陷入局部最优。

3 仿真试验及结果分析

本节采用Matlab/Simulink，验证所提方法的有效性。 在对作动器安装位置进行优化之前，需预先规定作动器的可选安装位置并进行编码。以现代航天器上常用的太阳能帆板为例，在如图3所示的有限元模型上均匀选取21组相邻节点作为可选安装位置。该太阳能帆板长7.38m，宽1.82m，有限元节点1354个，其具体挠性参数如表1所示。

表1 航天器挠性帆板参数Tab.1 Parameters of a flexible solar panel

为了便于计算，本文采用3个作动器对挠性结构的前3阶模态进行控制，并设计作动器的最优安装位置。根据优化指标式(12)，对作动器安装位置进行优化，在如图3所示的21个可选安装位置中选取3个作为作动器的最终安装位置。优化结果如图4至图7所示，在采用遗传算法优化过程中，种群最大适应度曲线如图8至图11所示，表2对上述仿真结果进行对比和归纳。

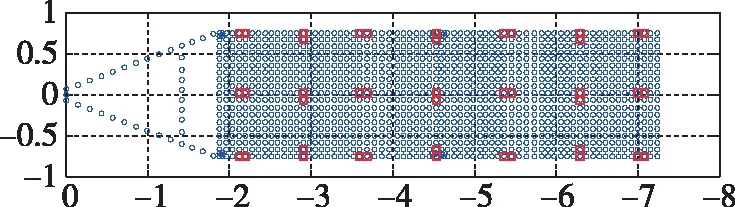
图3 可选安装位置示意图Fig.3 Optional positions of actuators

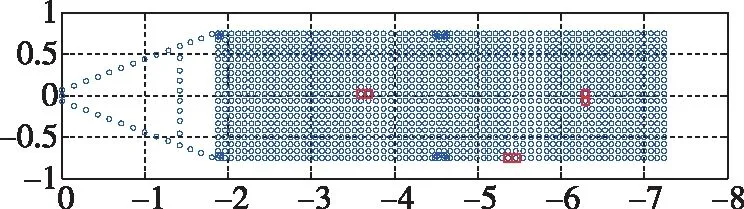
图4 最优安装位置 (μ=0)Fig.4 Optimal configuration of actuators with μ=0

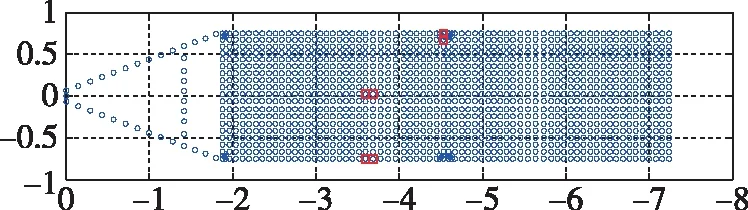
图5 最优安装位置(μ=2.2*10-5)Fig.5 Optimal configuration of actuators with μ=2.2*10-5

图6 最优安装位置(μ=4.0*10-5)Fig.6 Optimal configuration of actuators with μ=4.0*10-5

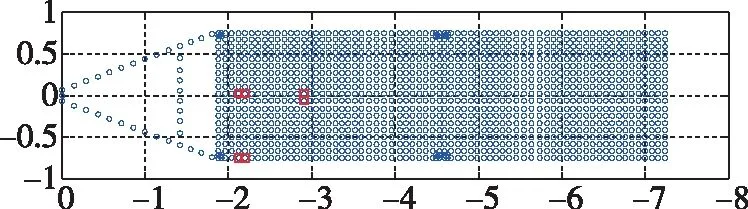
图7 最优安装位置(μ=6.3*10-5)Fig.7 Optimal configuration of actuators with μ=6.3*10-5

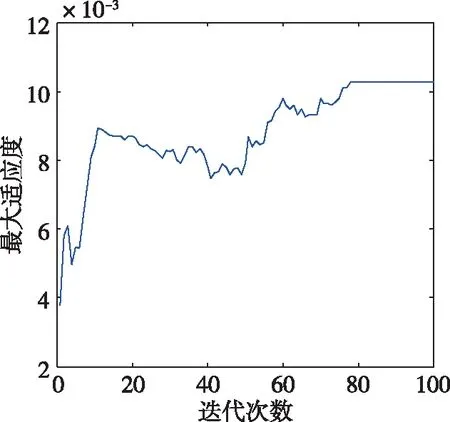
图8 种群最大适应度曲线(μ=0)Fig.8 The maximum population fitness with μ=0

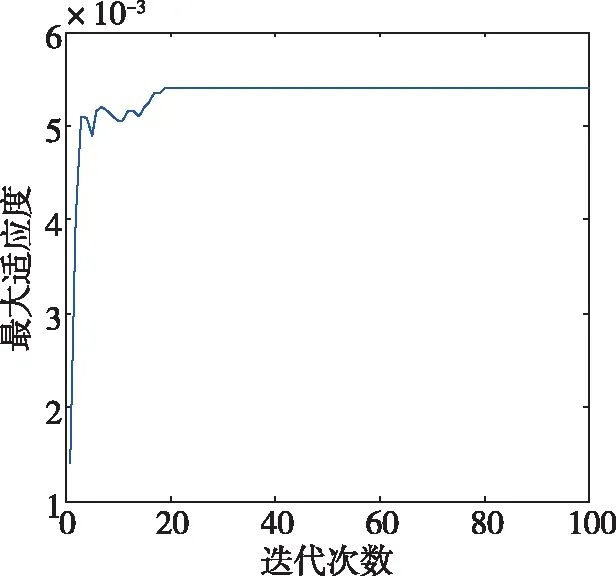
图9 种群最大适应度曲线(μ=2.2*10-5)Fig.9 The maximum population fitness with μ=2.2*10-5

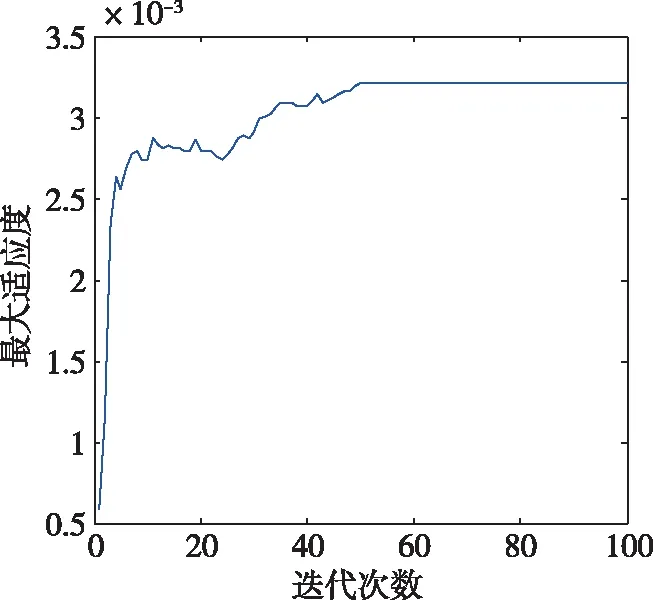
图10 种群最大适应度曲线(μ=4.0*10-5)Fig.10 The maximum population fitness with μ=4.0*10-5

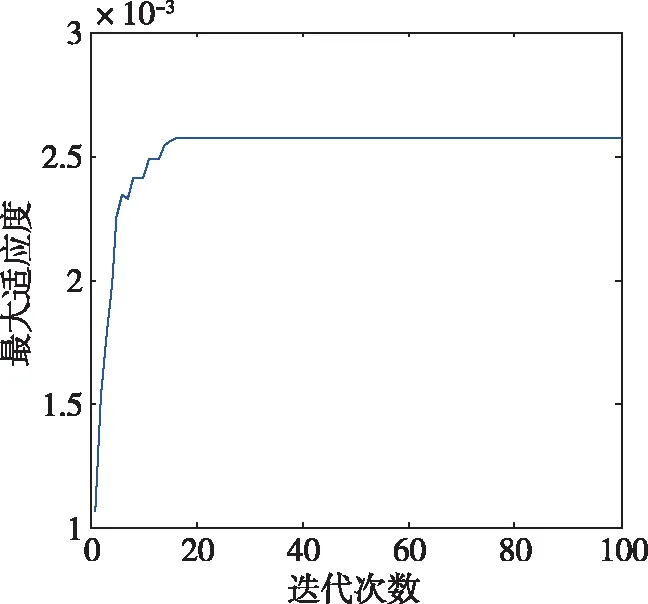
图11 种群最大适应度曲线(μ=6.3*10-5)Fig.11 The maximum population fitness with μ=6.3*10-5

表2 仿真结果总结Tab.2 Summarize of the simulation results

根据图8至11可知，种群最大适应度在不同情况下均能收敛于一个固定值，这说明遗传算法通过一定次数的迭代后找到了作动器的最优安装位置。由图4至图7及表2可知，优化指标(12)中的加权系数越大，优化结果中作动器的电缆越小，与理论分析结果一致，说明改进的优化指标兼顾了系统状态可控度及作动器电缆长度，证明了优化指标的有效性。

4 结 论

本文针对航天器挠性附件的振动抑制问题，研究了作动器的优化配置方案。综合考虑闭环系统的可控度和作动器的电缆长度，提出了一种新型的复合优化指标，该指标在保证系统对振动的抑制能力的前提下，能够有效缩减作动器电缆长度，减小航天器在轨运行期间的能量损耗和电磁干扰，具有较高的工程应用价值。在此基础上，采用遗传算法，实现了作动器安装位置的快速寻优。本文以挠性太阳能帆板的前三阶模态振动为例，通过大量数值仿真验证了所提方法的有效性。