一种柔性可展桁架结构的主动振动抑制技术*

朱东方，刘付成，黄 静，孙禄君，黄庭轩

(1. 上海航天控制技术研究所·上海·201109；2.上海市空间智能控制技术重点实验室·上海·201109)

0 引 言

随着空间遥感探测任务对高品质载荷的需求不断提升，航天器的结构尺寸不断趋向大型化发展。随着航天器结构尺寸的增大，传统机械结构在质量、体积和成本等方面的代价越来越大，并且由于机械展开式大型空间机构有大量旋转关节或驱动机构，使得其制造复杂和可靠性差。相对于传统机械结构存在的上述弊端，采用形状记忆复合材料(Shape-Memory-Polymer-based Composites，SMPC)的可展桁架结构凭借其质量小、形状回复率大、结构稳定等优点，在航空航天领域得到了迅速发展与应用[1-3]。

同时，柔性可展桁架结构的自由度高、构型复杂、运行环境特殊，使得对其进行动力学分析时建模难度大、耗时耗力，且难以用于结构的设计与振动控制。因此，建立复杂柔性可展桁架结构的合理简化模型是开展动力学分析与控制的关键之一。Noor等提出了空间周期性桁架结构连续体等效模型研究方法[4-7]，基于能量等效原理，分别将梁式和板式的周期桁架单元等效为梁模型和板模型，得到了等效连续体模型的刚度和质量系数，并通过静力学、动力学和热分析验证了等效模型的精度。Lee运用能量等效原理将周期桁架结构等效为考虑拉伸、剪切与弯曲之间耦合的Timoshenko梁模型，结合有限单元法推导等效连续梁结构的刚度和质量矩阵，并对其进行了结构振动特性分析[8]。郭宏伟和杨慧等对直线式类梁桁架和环形类梁桁架进行了连续体模型等效，对其振动特性进行对比分析[9-10]。刘福寿等研究了环形周期桁架结构的等效连续体模型，对环形桁架结构面内和面外的振动特性进行了分析[11]。虽然连续体等效建模可以对柔性桁架结构的动力学特性进行分析，但较难建立适用于含作动执行机构的智能桁架结构主动振动控制器设计的动力学模型。为了建立上述模型，需要采用能够保留局部作动执行机构特性的建模方法。模态综合建模方法是将整体结构按照一定策略进行分解，分析分解得到的多个子结构系统动力学特性，然后将子结构按照原始界面几何连续原则进行装配连接，根据子结构间存在不独立坐标得到动力学方程，最终建立整体结构动力学模型。由于模态变换过程中，针对各个子结构仅选取少数模态进行综合，因而通过子结构方法降低整体结构求解阶数，既能提高计算效率，同时还可以对更大更复杂的模型进行仿真计算。Hurty于20世纪60年代首次提出固定界面模态综合技术[12]，Craig和Bampton提出Craig-Bampton方法对Hurry的固定界面模态综合技术进行改进[13]，目前自由界面模态综合技术通常指Craig-Bampton方法。自由界面模态综合技术由Hou S N于1969年提出，综合过程中完全将高阶模态忽略导致计算精度难以保证，Rubin在剩余柔度基础上引入剩余惯性项，提出2阶近似剩余模态综合方程极大提高了计算精度[14]，王文亮等采用李兹法给出自由界面模态综合方程[15]。杨文山等采用模态综合方法研究了一种基于子结构方法的舰艇整体结构模态信息求解方法和水下爆炸载荷作用下冲击环境预报技术[16]。

在建立了柔性结构动力学模型后，需要设计适用的控制器实现对其挠性振动抑制。主动振动抑制控制理论也是研究的重点，目前学者们已经研究了许多控制方法可以有效地抑制大型柔性结构的振动，例如混合正反馈(Hybrid Positive Feedback，HPF)控制设计[17]、正位置反馈(Positive Position Feedback，PPF)[18]、基于最小能量的控制器[19]、基于Lyapunov函数的非线性振动系统的控制方法[20]、极点-配置-积分谐振控制方法等[21]。随着柔性结构的尺度变大，控制元件的选择和控制方法的合理设计是两个影响抑振效果的主要因素。Wang等使用可控性指标对压电执行机构-传感器对的尺寸和位置进行了优化[22]。Yang等采用最大化的能量耗散作为性能指标实现执行机构的优化配置与系统的控制[23]。Liu等将闭环传递函数矩阵的空间H2范数作为执行机构优化配置的性能指标[24]。Güney等提出了同时设计H∞控制器和优化执行机构传感器位置方法[25]。当给定执行机构的优化性能指标后，需要考虑如何求解最优位置。不同的方法已经用于求解最优配置问题，如禁忌算法、粒子群算法、模拟退火算法、遗传算法等。尽管Wang等使用粒子群算法实现了执行机构的最优配置，但是粒子群算法在求解最优配置问题中只能得到非凸函数的全局最优解[26]。Sadri等使用遗传算法得到了各向同性板上执行机构的优化位置[27]。Sheng等研究了一系列的微型遗传算法用于大量数目的执行机构的优化配置问题，讨论了微型遗传算法在不同随机种子产生器、不同算法重启标准以及不同数目执行机构条件下的求解效果[28]。虽然上述研究方法针对典型结构或典型问题目前已经取得了相应研究成果，但对于柔性可展桁架结构的主动振动抑制问题需要开展针对性的研究。

本文针对采用形状记忆复合材料的智能柔性可展桁架结构，首先基于模态综合的方法建立其整体动力学模型，然后采用动态滑模控制律设计主动振动控制器，并基于遗传算法对作动执行机构的布局配置进行优化，最后通过数值仿真验证所设计方法的有效性和精度。

1 智能柔性可展桁架结构动力学建模

智能柔性可展桁架结构是柔性可展桁架结构与作动执行机构共同构成。作动执行结构串接在柔性可展桁架结构内部，主要是在柔性可展桁架结构展开锁定的状态下工作；在保证柔性可展桁架结构具备相应刚度的基础上，提供作动执行力矩，实现对柔性可展桁架结构挠性振动的主动抑制控制。

1.1 柔性可展桁架结构的动力学模型

柔性可展桁架结构采用文献[29]中的结构形式，主要由复合材料纵梁、连接隔板、斜拉索和矩阵板构成，横截面为三角形，展开锁定后的柔性桁架结构如图1所示。

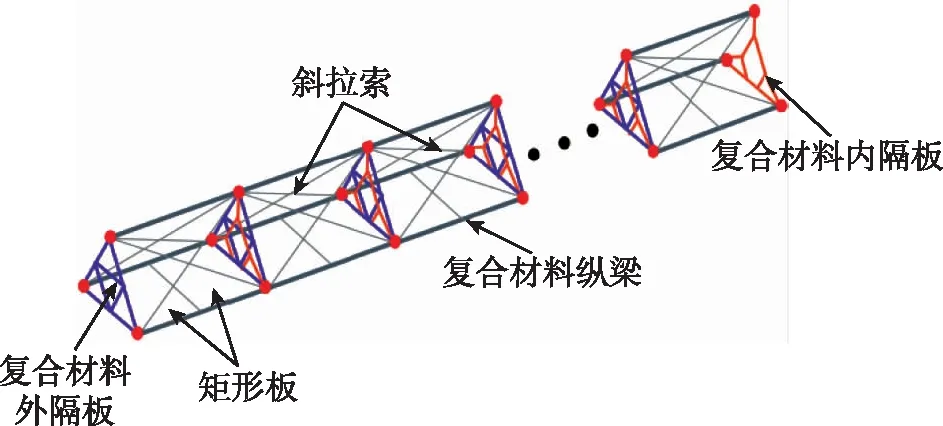
图1 柔性可展开桁架结构示意图Fig.1 Schematic diagram of the integral structure

根据图1中柔性可展桁架整体结构的几何特征可见，其结构具有周期特性，单节桁架结构可作为其周期胞元。对于超大尺度的柔性可展桁架结构，为了建立适用于控制器设计的低阶动力学模型，结合其周期性特征，采用固定界面模态综合建模方法。单节桁架结构采用有限单元法对结构进行离散化(见图2)，将连接界面的交界面节点自由度定义为界面自由度，将其余节点统称为内部节点，相关自由度定义为内部自由度。

图2 单节桁架结构有限单元法离散后节点定义Fig.2 The nodes of a single truss structure discretized by the finite element method

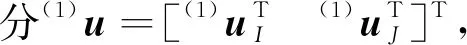
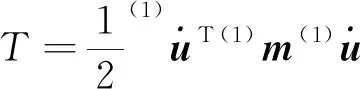
(1)

其中(1)m和(1)k分别为质量矩阵与刚度矩阵。

为了建立低阶模型，将物理坐标(1)u变换到模态坐标(1)p，并选择交界面节点的物理坐标作为广义坐标，则采用模态坐标描述为

(2)

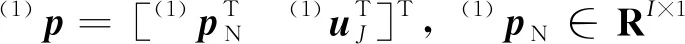
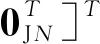
在(1)ΦN中略去对系统响应贡献度较小的高阶模态，仅保留k阶主模态(1)Φk时，自由度减缩后的变换为

(3)

其中，固定界面主模态(1)Φk可通过求解界面固定状态下的单节桁架结构动力学方程得到，约束模态(1)ΨIJ可通过逐一释放界面自由度使其产生单位位移而得到的各组静态变形构成。

将式(3)代入式(1)，建立单节桁架结构模态坐标方程为

(4)

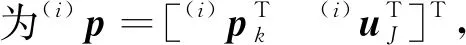
(5)

根据界面位移协调条件(i)uJ=(i+1)uJ，则柔性可展开桁架结构的模态坐标可转换为

(6)

其中，T2为波尔矩阵，(c)uJ表示所有子结构各界面中的独立节点坐标向量。

p=T1T3q

(7)

根据式(4)和式(7)，可以建立由各子结构动力学方程组装成的总体动力学方程为

(8)

其中，

1.2 作动执行机构的动力学模型

作动执行机构提供两个方向的控制力矩，实现对柔性可展开桁架结构弯曲振动形态的主动控制。作动执行机构的原理图和结构图如图3所示。

(a)原理图

(b)结构图图3 作动执行机构的原理图与结构图Fig.3 The schematic and structural drawings of the actuator

根据图3中定义，建立作动执行机构的力矩平衡方程为

(9)

其中，M表示音圈电机产生的力矩，J表示动平台转动惯量，θ表示动平台转动角度，c表示系统阻尼系数，mc表示电机动子质量，l表示转动力臂，x表示电机运动距离。

结合音圈电机原理，建立系统的动力学方程为

(10)

其中，c′表示音圈电机阻尼系数，Km表示音圈电机驱动力系数，Ks表示电机力常数，R表示电阻，k表示系统刚度，I表示线圈中的电流。

由于作动执行机构转动角度非常小，采用线性近似关系tan(θ)≈θ。由式(9)和式(10)，建立作动执行机构单自由度传递函数为

(11)

同理，可以建立作动执行机构另外一个自由度的传力函数。

1.3 智能柔性可展桁架结构的动力学模型

对于智能柔性可展桁架结构，是将作动执行机构安装在柔性可展桁架结构内部，提供相应的控制力矩。根据式(8)和式(11)，建立智能柔性可展桁架结构的动力学模型为

(12)

其中，Fc表示作动执行机构的控制力矩，F表示柔性可展桁架结构所受外部激励作用。

2 智能柔性可展桁架结构主动振动控制器设计

(13)

其中，A=-M-1K，B=M-1。

为了提高主动振动控制器的鲁棒性，更好地适应系统未建模动态的影响，采用鲁棒性较强的滑模变结构控制方法设计控制律。为了降低滑模变结构切换控制律的高频切换抖动影响，采用动态滑模控制理论设计控制器，将不连续项转移到控制的一阶导数中，从而得到在时间上本质连续的动态滑模控制律。

定义系统的误差和切换函数分别为

(14)

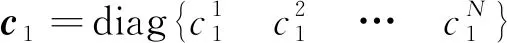
则

(15)

构造新的动态切换函数为

(16)

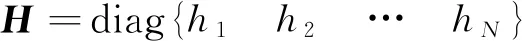
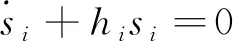
根据到达条件，采用等速趋近律，设计系统的动态滑模控制律为

(17)

将控制律(17)积分，可以得到系统(13)的动态滑模变结构控制律，然后结合式(11)可以获得作动执行机构的实际输出力矩。

3 作动执行机构布局优化配置

在柔性可展桁架结构复合材料纵梁的折叠约束下，为了保证作动执行机构的输出能力，将作动执行机构安装柔性可展开桁架子结构连接的交界面节点处。为了实现作动执行机构最少的数量对柔性可展开桁架结构的主动振动控制，需要对作动执行机构的位置进行布局优化配置。

为了反映控制器增益、作动执行机构位置及数目与柔性可展桁架机构振动控制性能间的影响关系，设计系统的线性二次型性能指标函数为

(18)

其中，Q和R分别为半正定的状态加权矩阵和正定的控制输入加权矩阵。

式(18)表示系统的能量主要由两部分组成，第一项为结构振动能量，第二项为控制能量。通过求解系统状态的Riccati方程，可以得到系统(13)的控制律为

Fc=-KX(t)=-R-1BTPX(t)

(19)

其中，P为如下Riccati方程(22)的正定解。

ATP+PA-PBR-1BTP+Q=0

(20)

当初始条件为X(0)时，t时刻方程的解为

(21)

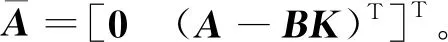
将式(19)和式(21)代入式(18)可得

(22)

在最小化性能指标约束下，通过求解Riccati方程，可同时实现控制增益和作动器布局优化配置。但由于性能指标函数与系统的初始状态有直接关系，可能会影响最终的优化结果，所以假定系统的初始状态是在n维单位球上均匀分布的随机量，用性能指标函数的平均值作为目标函数进行计算，以避免系统初始状态的影响。

则式(22)可转化为

(23)

对于优化问题(23)，可采用遗传优化算法等多种智能优化算法进行求解。

4 仿真研究

选择4节桁架子结构构成的桁架结构作为仿真对象，桁架结构的几何尺寸参数和材料属性参数如表1和表2所示。

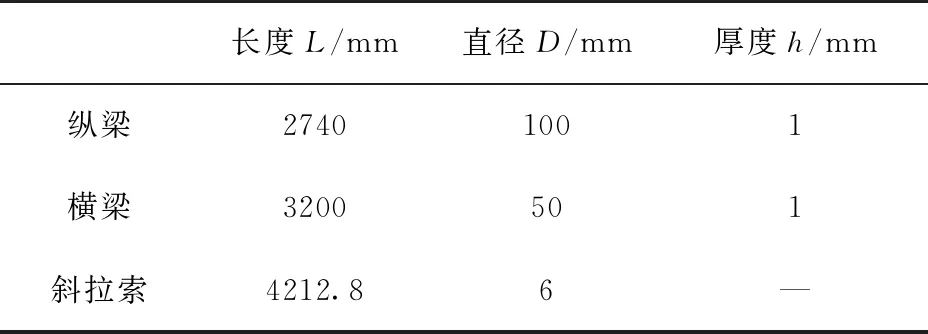
表1 桁架结构的几何尺寸参数 Tab.1 Geometrical parameters of truss members

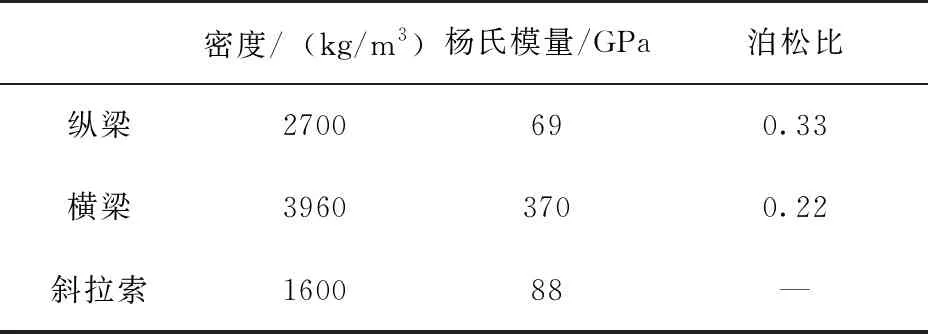
表2 桁架结构的材料属性参数Tab.2 Material parameters of truss members

根据上述参数，采用1节中的建模方法，每个子结构保留7阶主模态，建立悬臂态的4节桁架结构动力学模型。然后将4个子结构的12个连接交界面节点处均作为初始候选位置，选择5个最优位置，采用遗传优化算法进行优化配置。优化后的作动执行机构的布局优化配置图如图4所示。

图4 作用执行机构布局优化初始位置(红点位置)与优化位置图(黑点位置)Fig.4 Optimized initial position (red spot position) and optimized position (black spot position) of actuators

优化后最优适应度值与平均适应度值收敛如图5所示。

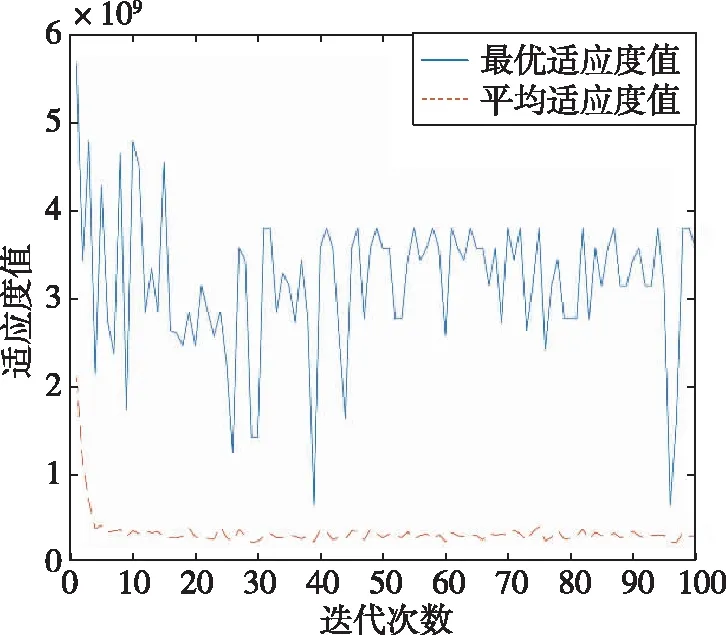
图5 最优适应度值与平均适应度值收敛曲线Fig.5 Convergence curve of optimal fitness value and average value

根据优化的作动执行机构位置，在4节桁架结构的自由端顶点前1s施加50N与矩形板法线平行的阶跃干扰力，采用动态滑模控制律(17)，进行闭环控制仿真。

图6 无控制下柔性桁架结构自由端节点位移响应Fig.6 Displacement response of free end node of flexible truss structure without control

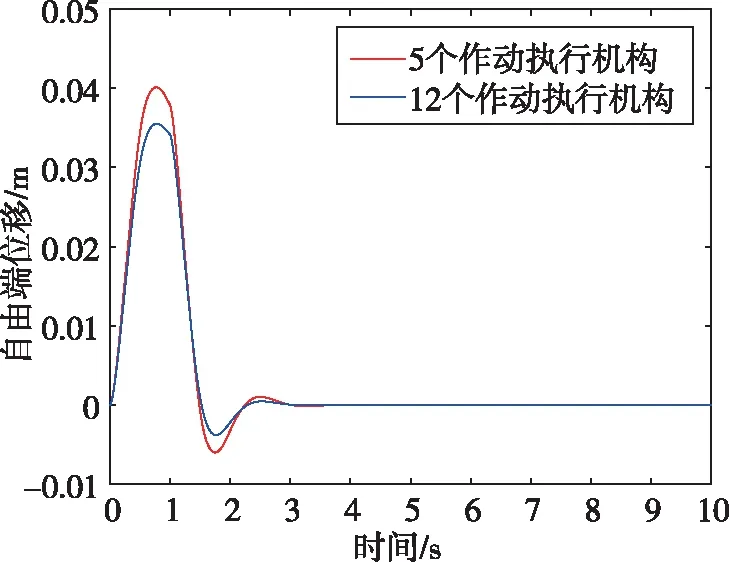
图7 不同数量作动执行机构作用时柔性桁架结构自由端节点位移响应Fig.7 Displacement response of free end node of flexible truss structure with different actuating actuators

从图6和图7对比可以看出，采用作动执行机构实施主动控制作用时，能够快速衰减柔性桁架结构的挠性振动，并且能够有效地降低干扰作用产生的振动的幅值。从图7中不同数量作动执行机构作用下柔性桁架结构的响应对比可以看出，经过布局优化配置后，仅采用5个作动执行机构即可实现与所有作动执行机构全部工作时相当的控制效果，验证了布局优化算法的有效性。

5 结 论

本文针对柔性可展桁架结构的主动振动控制问题，采用模态综合方法、动态滑模控制方法和遗传算法等提出一种主动振动控制器设计方法。主要结论如下：

(1)根据柔性可展桁架结构的周期性几何特征，采用模态综合方法在建立周期胞元单节桁架结构的降阶模型基础上，基于固定界面协调条件，综合建立整体桁架结构适用于控制器设计的低阶模型；进而建立作动执行机构的动力学模型，建立智能柔性可展桁架结构的动力学模型。

(2)针对柔性可展桁架结构易受到外部干扰影响问题，设计了鲁棒性强的动态滑模控制器，将不连续切换项引入到控制的一阶导数，大大削弱了控制作用的高频抖动。

(3)设计了作动执行机构布局优化配置的线性二次型性能指标函数，采用遗传算法获得了最优安装位置。

(4)仿真结果表明，所设计的主动振动控制器保证了系统的鲁棒性，达到了控制要求，具有较好的工程应用前景。