基于封严间隙的涡轮盘篦齿综合优化设计

陈志英，汪宇峰，刘 勇，赵连鹏

（北京航空航天大学能源与动力工程学院，北京100191）

0 引言

随着航空发动机涡轮前温度和增压比的提高，对封严装置的性能要求也相应提高。封严效率以流量系数为评价指标，转、静子之间的径向间隙是影响封严效率的重要因素[1]。径向间隙越小，泄漏量越小，有利于提高发动机气动性能，但是径向间隙过小会导致转、静子之间碰摩，引发部件磨损和整机振动等问题[2]。因此，如何合理设计涡轮篦齿间隙，保证航空发动机持续稳定工作，一直是专家学者研究的重点。李云菊等[3]对涡轮盘封严篦齿裂纹进行故障诊断，结果显示篦齿内部不同齿的形变量存在差异；龚梦贤等[4]的研究表明，为提高发动机性能而提高涡轮前温度的做法会加大篦齿的形变和应力，引起碰摩和局部高温；王锁芳等[5]对直通型篦齿的研究表明，泄漏系数与篦齿间隙成正比关系。针对发动机中转、静子之间的间隙，Howard W D、Olsson W J等[6-7]采用试验与数值计算相结合的方法分析，Zhao W D等[8-9]研究表明离心载荷、温度载荷、转子不平衡响应是影响涡轮径向间隙的主要因素；从结构概率设计的角度分析发现这些因素呈现一定的随机性，可以认为其服从某种分布[10]，因而间隙值与确定性分析相比会存在一定的偏差，可能导致篦齿封严间隙存在较大的概率分布区间。国内外学者对篦齿发生碰摩故障的原因、封严间隙与封严效率之间的关系、影响间隙的主要因素等都有深入研究。然而对工作状态下多道篦齿径向形变不一致以及碰摩概率的定量分析则鲜有涉及；传统结构优化设计也欠缺优化前后的流场分析对比；对于考虑间隙与封严效率之间关系的篦齿改进设计也缺乏深入实践。

本文从涡轮级间封严篦齿径向间隙出发，考虑各随机变量的分散性，将涡轮盘相关尺寸参数作为设计变量，不同齿的间隙作为目标函数，轮盘质量与碰摩概率作为重要约束，运用NSGA-II算法进行优化设计，并引入流场分析对封严效率进行验证。

1 稳态篦齿间隙计算

通过对篦齿间隙的有限元计算进行确定性分析，并通过结构尺寸灵敏度和篦齿间隙概率分析确定优化设计的设计变量和优化目标。

1.1 篦齿间隙确定性计算

涡轮级间篦齿封严间隙D由内、外环装配关系决定（如图1所示），封严间隙为封严外环内径r1与封严内环外径r2的差值

图1 篦齿封严间隙关系

篦齿间隙受转子离心载荷、热载荷、转子不平衡振动等多种因素综合影响，本文以浮动整环式级间封严方案为研究对象，该封严形式的特点是通过转、静子之间热响应特性的匹配设计，使封严外环随工作状态实现自动浮动[11]，从而达到封严的目的，即封严外环径向位置由工作状态确定，所以式（1）可写为

式中：R2为工作状态下发动机篦齿内环外径的设计值；D0为工作状态下发动机封严间隙的设计值；α为转子不平衡振动造成的间隙变化。

涡轮盘装配有90个工作叶片，因而建立1/90循环对称结构模型，不考虑涡轮盘的冷却通气孔，材料选用高温合金GH4169，有限元模型如图2所示。

为尽可能真实地模拟涡轮盘的工作情况，主要载荷及边界条件如下。

（1）叶片高速旋转产生的离心力以均布载荷的形式加载到轮缘表面[12]，根据估算加载到轮缘表面的压力为170 MPa。

（2）通过施加给模型转速来模拟轮盘最大工作状态的离心力，转速为13300 r/min。

（3）采用涡轮盘温度分布经验公式来模拟热载荷

图2 涡轮盘有限元模型

式中：Tb为盘心温度；Tr为盘缘温度；Rb为盘心半径；Rr为盘缘半径；R为半径。

（4）对涡轮盘与高压轴连接的安装边施加法向与轴向的位移约束，模拟涡轮盘安装情况。

涡轮盘上的3道封严篦齿的径向设计尺寸一致。而计算结果显示3道篦齿径向形变不一致，篦齿距离轮盘中心的轴向距离越远，径向形变越大，如图3所示。

图3 篦齿径向形变结果

取3道篦齿各自的最大形变量。此工作状态下，中间篦齿间隙设计值取0.400 mm，可得3道篦齿径向间隙

式中：Di为第i道篦齿的径向间隙；Si为第i道篦齿的径向形变。3道篦齿的径向形变量与间隙见表1。

表1 稳态下篦齿径向形变与间隙 mm

1.2 结构尺寸灵敏度分析

结构尺寸因为加工等原因有一定的不确定性，利用灵敏度分析找出影响篦齿封严间隙和涡轮盘质量的关键尺寸作为不确定性变量，引入概率分析中，同时为后续优化设计确定关键的设计变量。

轮盘的内、外缘和轮盘与轴颈连接处的尺寸，以及可直接改变封严间隙的尺寸均不能轻易改动。因此本文选取轮毂、辐板和篦齿轴向的结构尺寸作为设计变量，如图4所示。图中P1为第3道篦齿距离轮盘轴向边缘的距离；P2、P3和P4为每道篦齿的轴向长度；P5为幅板外径；P6为轮毂高度；P7为幅板厚度；P8为轮毂厚度；P9、P10为轮毂上、下两侧圆角半径。尺寸参数在不改变结构拓扑关系的变化范围内。

图4 涡轮盘尺寸参数

采用拉丁超立方体抽样设计方法[13]建立149个试验点，考察影响涡轮盘质量与篦齿径向间隙的关键尺寸，对10个结构尺寸进行灵敏度分析。结果如图5所示，图中M为涡轮盘质量。

图5 结构尺寸灵敏度分析结果

由灵敏度分析结果可知，P1、P2、P3、P5是影响篦齿间隙的关键尺寸，P5、P8是影响涡轮盘质量的关键尺寸，因此选择 P1、P2、P3、P5、P8作为设计变量代入到后续分析中。

1.3 篦齿间隙概率分析

考虑尺寸参数、工况载荷、材料参数的分散性，对涡轮篦齿径向间隙进行概率分析。其中发动机转速的控制精度为±2%，转速随机变量ω的标准差为(ω×2%)/3，叶片旋转产生的离心力P的标准差可通过与转速ω的关系求得，材料参数弹性模量E和泊松比v变异系数为0.02，尺寸参数取原尺寸的区间，假设以上参数均满足正态分布，抽样范围均为±3σ，相关数据见表2。

表2 随机变量的统计特征

基于确定性有限元模型，采用拉丁超立方体抽样设计方法抽取147组数据作为训练样本进行有限元分析。将147次试验数据作为训练样本进行Kriging响应面[14]拟合，得到3道篦齿间隙的响应面函数

再计算30组数据作为校验样本对响应面拟合情况进行校验，并利用决定系数R2和均方根误差e评价响应面拟合精度，其中R2越接近1，表示训练样本拟合越好；e越接近0，表示拟合精度越高[15]。决定系数和均方根误差为

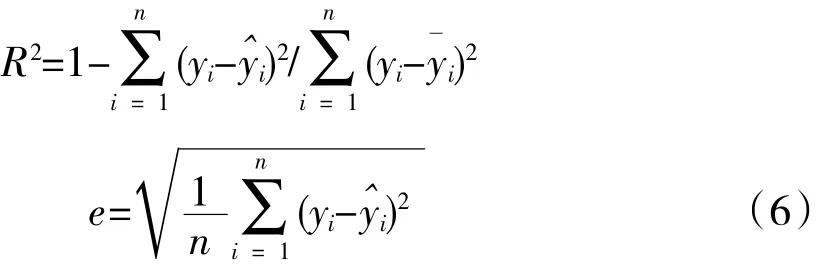
式中：n为样本数量；yi为第i个样本值；y^i为利用代理模型得到的预估值；y¯为所有样本点相应点的平均值。

训练样本与校验样本拟合结果如图6所示。从图中可见，训练样本与校验样本的预测值均与真实值较为接近，说明代理模型拟合情况良好。

图6 训练点与校验点拟合情况

计算得到的3道篦齿间隙的决定系数与均方根误差见表3。

表3 响应面精度参数

训练样本的决定系数均为1，训练样本和校验样本的均方根误差均非常接近0，说明响应面拟合精度高，满足使用要求。

响应面建立之后，进行100万次随机抽样，得到3道篦齿间隙D1、D2、D3的概率分布，如图7所示。

图7 篦齿间隙概率分布

由飞行器机动飞行引起的转子径向不平衡振动幅值叠加变化范围约为0.30 mm[16]，则当不平衡振动为0.30 mm时，结合式（2）得到第3道篦齿发生碰摩的概率为

2 综合优化设计

对篦齿结构进行优化以达到降低篦齿碰摩概率的目的，同时优化后的结构有相应约束条件：涡轮盘质量不增加、封严效率不降低。

2.1 NSGA-II算法

多目标优化是指在某种条件下对多个数值目标同时优化。遗传算法是1种模仿生物界自然选择与自然遗传机制的随机搜索算法，其中Deb等[17]提出的NSGA-II方法具有收敛性好、收敛速度快和多样性的优点，在航空领域被广泛应用于结构优化设计[18-20]。

NSGA-II算法优化过程为：首先随机产生初始种群P0，进行非支配排序，随后利用选择、交叉、变异等遗传算法操作得到第1代子代种群Q0；第2代开始，对把父代种群Pn与子代种群Qn合并而来的种群Rn进行快速非支配排序，得到非支配前端F1，F2……；对非支配前端中的个体进行拥挤度计算，选取合适的个体组成新的父代种群Pn+1；之后通过选择、交叉、变异等操作生成新子代种群Qn+1，一次进化操作完成；迭代，当达到终止条件时停止运算，得到多目标优化问题的Pareto非劣解集。主要过程如图8所示。

图8 NSGA-II算法主要过程

2.2 综合优化模型

基于NSGA-II优化方法建立优化模型。优化设计时，需要增大第3道篦齿的封严间隙以降低其碰摩概率，以正态分布的“3σ”原则为约束条件，即第3道篦齿不发生碰摩的概率应不低于99.74%，有

前2道篦齿无碰摩风险，因此基于保证封严效率的原则，需减小前2道篦齿的封严间隙。则分别约束D1与D2不大于原始设计值，同时涡轮盘质量不大于原始设计值，目标函数求D1与D2的最小值尺寸参数在不改变轮盘拓扑结构的变化范围内。X=（P1,P2,P3,P5,P8）为尺寸设计变量，建立多目标综合优化模型

初始筛选样本为1万个，经过15次迭代，11337次求值，得到优化结果。D2迭代计算过程如图9所示。

优化前、后的涡轮盘关键设计尺寸对比见表4。

图9 迭代计算过程

表4 优化前、后参数对比 mm

结合结构尺寸灵敏度分析结果，对比优化设计前、后的结构可知，为增大第3道篦齿间隙，延长了第3道篦齿到轮盘轴向边缘的距离；为减小前2道篦齿间隙，延长了前2道篦齿到轮盘中心距离、减小了幅板外径；为保证涡轮盘质量不大于原设计质量，减小了轮毂厚度。

径向间隙、质量与初始设计对比见表5。

表5 优化前、后结果对比

从表中可见，前2道篦齿间隙分别减小了7.07%、3.00%，第3道篦齿间隙增加了3.61%，涡轮盘质量降低了0.73%，满足优化目标和约束条件。

对优化后的篦齿间隙进行不确定性分析，第3道篦齿间隙优化前后概率分布曲线对比如图10所示。

图10 优化前、后第3道篦齿间隙概率分布对比

计算结果表明，径向振动值为0.30 mm时，第3道篦齿发生碰摩的概率为0.173%，满足约束条件，优化后涡轮盘篦齿碰摩风险大大减小。

2.3 封严效果分析

在篦齿封严中，流量系数Cd是评价封严效果的重要依据[21]，其表达式为

式中：m˙为实际质量流量；m˙ideal为理想质量流量；p1*、p4、T1*分别为进口总压、出口总压和进口总温；A1为篦齿流道最小流通面积；Rg、κ分别为气体常数和绝热指数。

针对优化前、后的篦齿结构进行流量系数计算，建立流场分析有限元模型，如图11所示。其中湍流模型为k-e模型，采用增强的壁面函数，壁面yplus小于1，模型进口为压力进口条件，出口为压力出口条件，壁面采用无滑移壁面边界条件。

图11 流场分析有限元模型

计算不同压比下的流量系数，对比优化前、后篦齿结构封严效果。得到的优化前、后的流量系数随进、出口压比变化的曲线如图12所示。

图12 优化前、后的流量系数随压比的变化关系

从图中可见，在不同压比条件下，优化后的流量系数比优化前的小5.39%～6.01%，说明优化后的结构封严效果更好。

优化前、后篦齿内部流道压力场分布如图13所示。

从图中可见，相对于优化前的流场，优化后的结构中气体流经优化后的第1个篦齿产生了激波系，气体压力相对降低更多，因此优化后出流气体压力更低，流量系数更小，优化效果显著。

图13 优化前、后流道压力分布

3 结论

本文以降低涡轮级间封严篦齿碰摩概率和保证封严效率为研究目标，对涡轮盘结构尺寸进行优化设计，得到如下结论：

（1）对篦齿间隙进行有限元计算的结果表明，在稳态工作条件下3道篦齿径向形变不一致，篦齿距离轮盘中心的轴向距离越远，径向形变越大，间隙越小；对篦齿间隙进行不确定性分析的结果表明，在考虑发动机转子不平衡振动情况下，第3道篦齿有发生碰摩的风险。

（2）多目标优化与流场分析结果表明，与优化前相比，优化后涡轮盘质量减小了0.73%，第3道篦齿发生碰摩的概率从18.580%降到0.173%；优化后的结构流量系数减小了5.39%～6.01%，证明优化后的篦齿设计碰摩风险大大降低并且封严效果更好，表明该优化方法的工程应用价值较高。

（3）对直通型篦齿结构的间隙计算和优化设计表明，综合考虑多道篦齿工作中的不协调形变引发的碰摩风险和封严效率的变化等因素，结合静力学分析与流场分析等多学科手段，对设计可靠性高、封严性能好的篦齿结构有一定的工程指导意义。