高性能二元收敛喷管型面设计方法
李 娜,吉洪湖
(1.南京工业大学能源科学与工程学院,南京211800;2.南京航空航天大学能源与动力学院,南京210016)
0 引言
在满足航空发动机推力性能设计要求的同时,喷管设计还希望获得高效率,以提高发动机的单位推力,降低耗油率。二元收敛喷管取代传统轴对称收敛喷管能够获得相对更好的红外隐身效果[1-3],但却牺牲了气动效率[4-7]。为此,需开展高性能参数二元收敛喷管型面设计方法研究。二元收敛喷管型面设计是指在喷管进、出口截面几何参数(进、出口截面面积和出口宽高比等)和喷管长度给定的情况下,根据喷管型面可以采用的描述方式,构造1个从发动机涡轮出口圆形截面光顺过渡到喷管出口矩形截面的高性能二元收敛喷管型面。采用纵向型线的描述方法难以得到合理控制和设计,而采用垂直于喷管轴线的横截面来描述[8-13],各横截面形状连续变化,可以形成光滑过渡的二元收敛喷管型面。20世纪80年代,文献[14]利用超椭圆方程可同时描述圆形至矩形等不同形状截面的特点,用于设计二元喷管的圆形到矩形转换段;文献[15]介绍了1种采用圆角矩形(4个直角采用圆弧过渡的矩形)设计超声速风洞圆形到矩形收敛段的方法。当选取不同的几何参数值时,圆角矩形也可以以统一方式描述从圆形到矩形连续变化的不同横截面形状,也可以用于设计二元收敛喷管型面。
本文借鉴超椭圆和圆角矩形的上述优点以及前人设计经验,发展和完善了基于超椭圆和圆角矩形截面的二元收敛喷管型面设计方法,并对横截面控制参数与沿程变化规律之间的几何约束关系进行探讨分析。
1 基于横截面的二元收敛喷管型面设计方法
1.1 基于超椭圆的二元收敛喷管横截面设计
1.1.1 超椭圆截面描述方法
圆转矩形的不同形状横截面如图1所示。若采用超椭圆方程描述图1中二元收敛喷管轴向任意x处的横截面,在y-z平面内,超椭圆方程为

图1 圆形转矩形的不同形状横截面
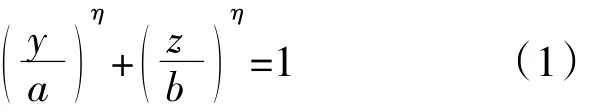
式中:a、b分别为超椭圆截面的长、短轴半径;η为超椭圆截面的可变指数。
当a=b,η→+∞时,式(1)描述的截面为圆截面;当η→+∞时,式(1)描述的截面形状逐渐趋近于方形或矩形。理论上,η趋于无穷大,超椭圆方程才能描述严格的直角矩形截面。但实际应用时,采用超椭圆截面设计二元收敛喷管时,出口截面不宜设计为严格的直角矩形,可以取η为较大的数(如50)来设计喷口矩形截面。
1.1.2 超椭圆截面控制参数
对任意超椭圆截面,当给定a、b、η时,超椭圆截面形状和面积完全确定,面积A为

式中:Г(·)为伽马函数

1.1.3 二元收敛喷管进、出口截面的超椭圆参数
在给定喷管进、出口截面几何参数(进、出口截面面积和出口宽高比等)和喷管长度的情况下,采用超椭圆截面设计二元收敛喷管型面,首先需要计算进、出口截面的超椭圆参数值。
假设二元收敛喷管进口圆截面面积为A7,进口圆截面直径D7=2,那么进口圆截面的超椭圆参数为

假设喷管出口截面面积(喉道面积)为A8、出口宽高比为AR(AR=a/b),同时假设出口截面为指数为ηe(取较大的数,如取ηe=50)的超椭圆截面,那么出口截面的其他超椭圆参数为

1.2 基于圆角矩形的二元收敛喷管横截面设计
1.2.1 圆角矩形截面描述方法
若采用圆角矩形描述二元收敛喷管轴向任意x处的横截面,在y-z平面内,圆角矩形可采用几何形状和参数来统一描述,如图2所示。从图中可见,圆角矩形4个直角均采用1/4圆弧过渡,a为圆角矩形的半宽,b为圆角矩形的半高,r为顶角圆弧半径。显然,当a=b=r时,圆角矩形变为圆,当r=0时,变为直角矩形。

图2 圆角矩形截面形状及参数
若采用数学方程来描述图2中的圆角矩形,那么在y-z平面第I象限内,圆角矩形方程可分段表示为

1.2.2 圆角矩形截面控制参数
对任意圆角矩形截面,当给定a、b和r时,圆角矩形的形状和面积完全确定,面积A为

若给定a、b和A,顶角圆弧半径r可由式(13)惟一确定

1.2.3 二元收敛喷管进、出口截面圆角矩形参数
采用圆角矩形截面设计二元收敛喷管时,进口圆截面的圆角矩形参数为

当出口截面为严格直角矩形时,出口截面的圆角矩形参数为
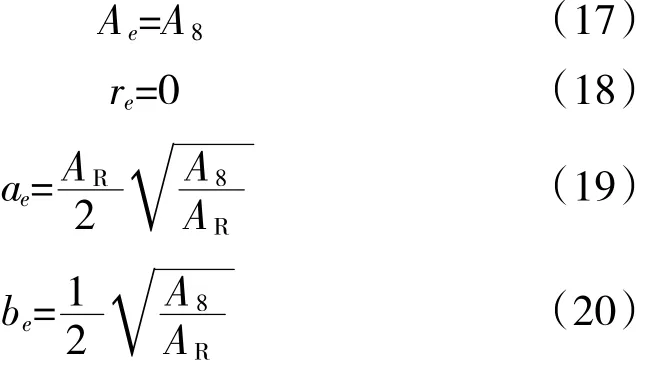
当出口截面采用顶角圆弧半径为re(>0)的圆角矩形时,出口截面的其他圆角矩形参数为

1.3 二元收敛喷管横截面控制参数沿程变化规律设计
为了使采用超椭圆或圆角矩形横截面设计的二元收敛喷管具有高的气动性能,需要对喷管截面控制参数沿程变化规律进行设计和控制。
假设喷管截面控制参数为p,p沿喷管轴向(x轴)的分布规律用函数p(x)表示,那么在进、出口截面控制参数值均已知的情况下(假设进口截面控制参数值为Pin,出口截面控制参数值为Pe),参数p的沿程变化规律p(x)可表示为插值函数形式

式中:x0为进口截面位置;L为喷管长度;φp(x)为截面相对位置x=(x-x0)/L的函数,且满足条件:φp(0)=0,φp(1)=1。
因此,在喷管进、出口截面参数已知的情况下,喷管截面控制参数沿程变化规律p(x)的设计可转变为截面位置函数φp(x)的构造和设计。
在给定喷管进、出口截面几何参数(进、出口截面面积和出口宽高比等)和喷管长度的情况下,无论采用超椭圆还是圆角矩形来描述二元收敛喷管的横截面形状,进、出口截面参数均是已知的。因此,φ(p0)=0和 φ(p1)=1是函数 φ(px)需要满足的基本约束条件。但要获得高的喷管气动性能,函数φ(px)还需要满足如下条件:
在函数 φp(x)需要满足的约束条件中,φ(p0)=0和 φ(p1)=1可称为零阶约束条件,(0)=0 和(1)=0可称为1阶约束条件。在满足上述零阶约束条件和1阶约束条件的同时,x从0变化至1时,(x)先从0逐渐增大,然后又减小至0,即在x∈(0,1)区间内,φ(′x)只存在1个极大值(当然也可能存在多于1个极大值的情况,但本文不考虑这种情况)。因此,函数 φ(px)还需满足如下2阶约束条件:在x∈(0,1)区间内,方程)=0 只有 1 个根。
应该说,满足上述要求的连续函数φp(x)的形式有无数种。选择如下多项式函数来构造函数φp(x)

式中:c0、c1、c2、c3、……为待定系数。
根据0阶和1阶约束条件,可得到

根据式(26)、(28)可知,要同时满足 0阶和 1阶约束条件,多项式函数的阶次不能低于2次。将c0=c1=0 代入式(27)、(29),可进一步得到
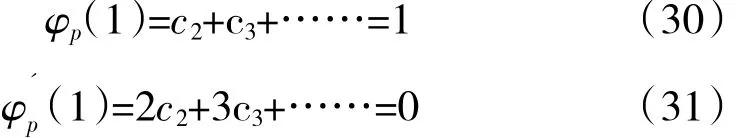
由上面2式可知,2次多项式函数不能同时满足式(30)、(31)。因此,同时满足0阶和1阶约束条件的多项式函数阶次不能低于3次。
根据式(30)、(31),结合 2阶约束条件,得到同时满足上述要求的3次和4次多项式函数。
3次多项式函数

4次多项式函数

式中:c4∈ -3,3[ ]且 c4≠0。若 c4=0,式(33)就变为如式(32)所示的3次多项式。
可以通过减少或增加约束条件构造出满足不同二元收敛喷管设计要求的更多其他函数关系,构造方法与上述过程类似,详细公式内容见文献[15]。而本文所构造设计的上述多项式函数已具有较好的代表性和典型性,为进一步研究高性能二元收敛喷管横截面控制参数沿程变化规律的选取打下基础。
上面构造的典型3次和4次多项式函数曲线如图3所示。
根据图中曲线的变化规律特点,可以将上述多项式函数分为典型的3类:第1类是进、出口函数值变化缓急程度一致的函数关系(图3中“Ⅲ型函数”),如:3 次函数,见式(32);第 2 类是进口函数值变化较为剧烈、出口函数值变化较为缓慢的函数关系(图3中“IV-2型函数”),如:4次函数φp(x)=6x2-8x3+3x4;第3类是进口函数值变化较为缓慢、出口函数值变化较为剧烈的函数关系(图3中“IV-1型函数”),如:4次函数φp(x)=4x3-3x4。
在喷管进、出口截面面积和出口宽高比、喷管长度给定的前提下,构造二元收敛喷管型面的关键步骤是选择横截面控制参数及各参数的沿程变化规律,由进、出口截面参数值计算喷管沿程中间截面参数值,从而形成各中间截面。多种喷管方案详细列表见文献[15]。

图3 4种典型多项式函数曲线
2 二元收敛喷管构型方案的数值计算分析
2.1 物理模型
以某混合排气涡扇发动机为基准发动机,基于其工作过程参数和设计点推力性能要求,开展混合排气二元收敛喷管设计研究。该发动机的原始喷管为固定式轴对称收敛喷管,由于采用混合排气方案,尾喷管同时起到混合室的作用,如图4所示。喷管喉道面积(以面积比A8/A7表示)为A8/A7=0.477,喷管长度(以长径比L/D7表示)为L/D7=0.465。对于混合排气喷管,喷管进口截面位置也是1个关键几何参数,本文以喷管进口截面到内涵出口截面之间的无量纲轴向距离N/D7表示,其中N为喷管进口截面至内涵出口截面之间的实际轴向距离。基准轴对称收敛喷管的该进口截面位置参数N/D7=0.129。

图4 基准轴对称收敛喷管几何模型
基于基准轴对称收敛喷管几何尺寸设计AR=4(出口矩形的宽高比为4)二元收敛喷管的几何模型。二元收敛喷管的喉道面积、喷管长度以及喷管进口截面位置均与基准轴对称收敛喷管完全相同。将轴对称收敛喷管修改设计为二元收敛喷管时,内涵通道和中心锥的几何形状和尺寸均保持原始设计不变。

图5 二元收敛喷管构型方案
为对比不同喷管的气动性能参数,分别对轴对称收敛外涵喷管、纵向型线二元收敛外涵喷管以及超椭圆和圆角矩形二元收敛外涵喷管进行分析,如图5所示。所有喷管均具有相同的进、出口截面面积和喷管长度(喷管进、出口截面面积比A8/A7=0.477,喷管长径比L/D7=1.0),所有二元收敛喷管的出口宽高比均相同(AR=4)。其中,超椭圆二元收敛喷管方案AⅢaⅢbⅢ是指选择长轴半径a、短轴半径b和面积A作为超椭圆截面的独立控制参数,同时,控制参数的沿程变化选择依据图3中的3次多项式函数。圆角矩形二元收敛喷管方案AⅣ-2bⅣ-2rⅣ-2是指选择矩形半高b、顶角圆弧半径r和面积A作为圆角矩形截面的独立控制参数,控制参数的沿程变化选择依据图3中的进口函数值变化较为剧烈、出口函数值变化较为缓慢的IV_2型函数。
2.2 数值计算结果
喷管流场计算模型分为内、外流场计算域,设喷管出口截面当量直径为D8,外流域圆柱体直径为10D8,长度为30D8。喷管进口总压均设为1.5×105Pa,进口总温设为500 K。外流场边界设置为压力出口,出口静压设为1.01325×105Pa,总温为300 K。采用结构化网格对计算域进行空间离散,计算网格总数约180万。
基准轴对称收敛喷管和AR=4超椭圆二元收敛喷管的内、外流场流线分布如图6、7所示。从图中可见,基准轴对称喷管的内涵气流基本是由外涵气流包围着沿喷管轴向流出,2股气流之间的掺混相对较弱。而二元收敛喷管的内涵气流基本占据了喷管射流的中心区域,外涵气流则被“挤”向靠近喷管出口“窄边”的两侧,内、外涵气流排出喷管后呈散射状,掺混程度相对比较强烈。

图6 基准轴对称收敛喷管的内、外涵气流流线

图7 AR=4的二元收敛喷管内、外涵气流流线计算结果

图8 二元收敛喷管宽、窄边对称面
二元收敛喷管的宽边对称面和窄边对称面如图8所示。在这2个对称面上,基准轴对称收敛喷管和AR=4超椭圆二元收敛喷管的射流速度分布特征如图9所示。从图中可见,轴对称收敛喷管的射流具有轴对称特征,在2个对称面上的速度分布完全相同,而二元收敛喷管在2个对称面上的速度分布存在显著差别,在宽边对称面上的速度分布呈现出“多峰”形貌。

图9 轴对称和AR=4二元收敛喷管在宽、窄边对称面上的x方向速度分量等值线分布
轴对称喷管、纵向型线二元喷管、超椭圆横截面二元喷管以及圆角矩形横截面二元喷管的流量系数和推力系数计算结果见表1。流量/推力的数值均是以基准轴对称收敛喷管的流量/推力为单位进行无量纲化的结果,喷管的总推力Fg为

式中:m˙8为喷管出口质量流量;U为喷管出口轴向速度;p8和pa分别为喷管出口静压和出口环境压力。
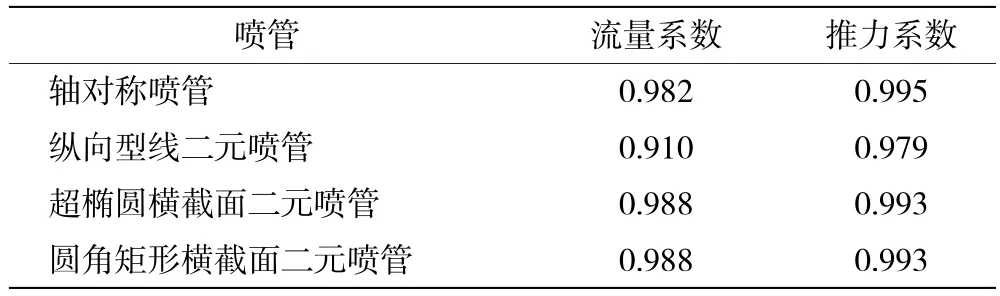
表1 不同喷管性能参数比较
从表中可见,纵向型线二元喷管的流量系数和推力系数明显低于轴对称喷管。超椭圆二元喷管AIV-2aIV-2bIV-2和圆角矩形二元喷管AIV-2aIV-2bIV-2均具有光顺过渡的几何外形,特别是采用了型面控制参数值在喷管出口附近平缓过渡的设计,使得喷管内流平稳,流动损失和非轴向射流动量损失明显降低,因此,该2种二元喷管的流量系数和推力系数均已比较接近轴对称喷管。
3 二元收敛喷管构型方案的试验分析
混合排气系统模拟试验台主要包括内涵燃气发生系统、供油点火系统、外涵气流系统和混合排气系统4大部分。内涵燃气发生系统主要由内涵风机和燃烧室组成,设计质量流量为1 kg/s。外涵气流系统主要由外涵风机和稳压腔组成,设计质量流量为1.2 kg/s。内、外涵气流质量流量均在一定范围内可调。供油点火系统主要由油箱、油泵、燃油控制台及高能点火器等组成,为燃烧室提供燃油和点火控制。混合排气系统主要由涡轮模拟件、中心锥、支板以及喷管等部件组成,较真实地模拟了某种涡扇发动机混合排气系统。混合排气系统可以换装不同类型喷管。内涵气流经燃烧室燃烧加热后,可以使涡轮模拟件出口截面的气流总温达到800 K以上,与所模拟的真实发动机实际涡轮出口气流总温比较接近。内涵高温燃气气流与外涵气流在混合排气喷管内混合并排入大气。
对原轴对称喷管和基于上述方法设计改型的出口宽高比分别为AR=2和AR=6的2种超椭圆截面二元收敛试验喷管进行试验研究。3种喷管总推力的数值计算和试验结果对比见表2。二者之间存在一定差别,但由数值方法和试验方法所得到的AR=2和AR=6的二元喷管的总推力与基准轴对称喷管的相对差别均在3%以内。考虑到试验件加工和试验测量误差,上述结果基本说明所设计的2种改型超椭圆截面二元喷管的总推力较接近于基准轴对称喷管的,同时也验证了数值计算方法的可靠性。

表2 3种喷管的总推力数值计算与试验结果对比
4 结论
本文主要开展了高性能二元收敛喷管型面设计方法研究。对比分析表明:采用纵向型线简单设计的二元喷管性能参数明显低于轴对称喷管的。而(超椭圆或圆角矩形)横截面构型的二元喷管具有光顺过渡的几何外形,特别是采用型面控制参数值在喷管出口附近平缓过渡(选用“IV_2型函数”)的设计,使得喷管内流平稳,流动损失和非轴向射流动量损失明显降低,其流量系数和推力系数均已较接近轴对称喷管的。由此可见,基于超椭圆或圆角矩形横截面构型二元喷管设计方法,通过选取合适的截面控制参数和沿程变化规律,均可设计出性能较高的二元收敛喷管。

