基于性能指标约束的一类输入死区非线性系统最优控制

郭子杰 白伟伟 周 琪 鲁仁全

不确定非线性系统控制问题一直是控制领域内研究的热点和难点[1−8].以模糊逻辑系统,神经网络为基础的自适应控制设计方法,打破了以往系统中非线性函数要满足某些限定条件或参数化的限制[1],解决了不满足匹配条件及不确定的非线性系统的控制器设计问题.并广泛应用于纯反馈和严格反馈的单输入单输出系统[2−3],多输入多输出系统[4−5],以及多智能体系统[6]中.值得注意的是,基于backstepping 技术的控制设计方法在每一步都需要对已设计的虚拟控制器进行反复求导,从而产生“计算爆炸”问题.而动态面控制技术通过在backstepping 设计的每一步中引入一阶低通滤波器,有效地避免了这一问题[9].在此基础上,文献[10]提出一种命令滤波方法,利用误差补偿机制消除动态面技术中滤波误差对系统性能的影响.上述工作为不确定非线性系统控制提供了一种简便化,结构化的方法,但以上成果均没有考虑最优控制问题.

最优控制是一类考虑系统控制性能和节能效应的控制策略[11].传统的动态规划(Dynamic programming,DP)采用按照时间阶段逆向递推的方法有效解决了最优控制问题[12],但其后向求解的模式往往会导致“维数灾”现象的发生[13].自适应动态规划(Adaptive dynamic programming,ADP)方法作为DP 方法的近似解法,弥补了DP 方法的不足,为求解复杂非线性系统最优控制问题提供了新的思路[14].Murray 等[15]首先针对连续系统提出了一种迭代ADP算法,并从数学上证明了该算法的可行性.Vamvoudakis 等[16]提出了基于策略迭代的在线ADP 方法,克服了迭代ADP 算法无法适应系统变化的缺点.上述的研究成果对ADP 理论的发展具有里程碑的意义.为了保证系统运行时的稳定性,文献[15−16]所提出的方法要求给定一个初始稳定的控制策略.针对此问题,Zargarzadeh 等[17]提出一种基于单网络评价技术的在线ADP 算法,并采用新的参数训练方法,突破了初始稳定控制策略的限制.近年来,ADP 受到国内学者的广泛关注[18−22],已经成为一种重要的优化控制方法.

目前,采用ADP 方法研究非线性系统的最优控制问题已经取得了一系列研究成果,然而针对带有输入死区和指定性能约束条件的非线性系统所做的研究较少.事实上,死区作为一类非光滑非线性函数经常出现在机械连接,液压制动器和传感器等实际工程系统中,极大地影响系统的性能,甚至引起系统不稳定[23].对此,文献[24−25]借助死区的斜率来解决输入死区问题.另一方面,工程中希望控制器不仅能够保证系统稳定,而且使系统跟踪误差在一定条件下收敛.文献[26]通过预先设定跟踪性能函数,提出一种指定性能方法,使得系统的跟踪误差保持在两个指定性能函数组成的有限范围内,解决了控制器设计参数调节难的问题.

基于以上讨论,本文针对一类考虑指定性能和具有输入死区约束的严格反馈非线性系统,提出一种自适应模糊最优控制方法.本文的主要工作如下:1)结合命令滤波技术和backstepping 方法设计了一种前馈控制器,与文献[19,27]的方法相比,本文采用命令滤波技术不但能克服“计算爆炸”问题,而且能补偿滤波器误差,取得更好的控制效果.2)设计了一种新的ADP 结构对误差系统进行优化,利用单网络在线逼近器求解近似最优控制器.3)本文解决了一类考虑输入死区和指定性能约束的非线性严格反馈系统的优化控制问题.最后,通过实例仿真验证所提控制方法的有效性.

1 问题描述

考虑一类严格反馈系统:

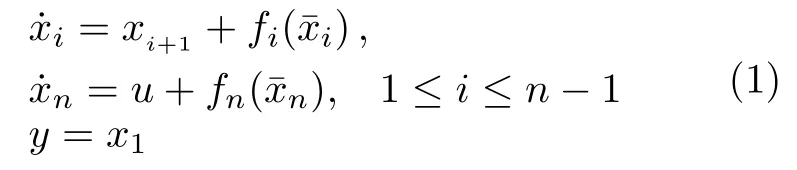
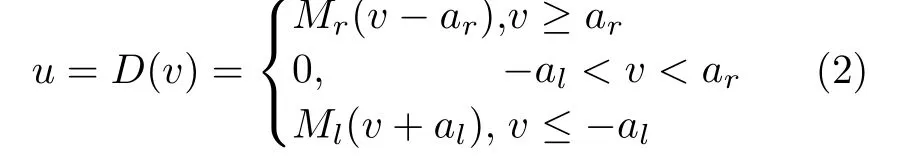
其中,v∈R是死区输入信号,Mr和Ml表示死区的斜率,al和ar是断点,Mr,Ml,ar,al都是正常数.

假设1[24].存在一个正常数ϖ满足|v|≤ϖ.

假设2[25].给定的参考信号x1d及其一阶导数是光滑的、已知的且有界.

死区输入(2)可简化为

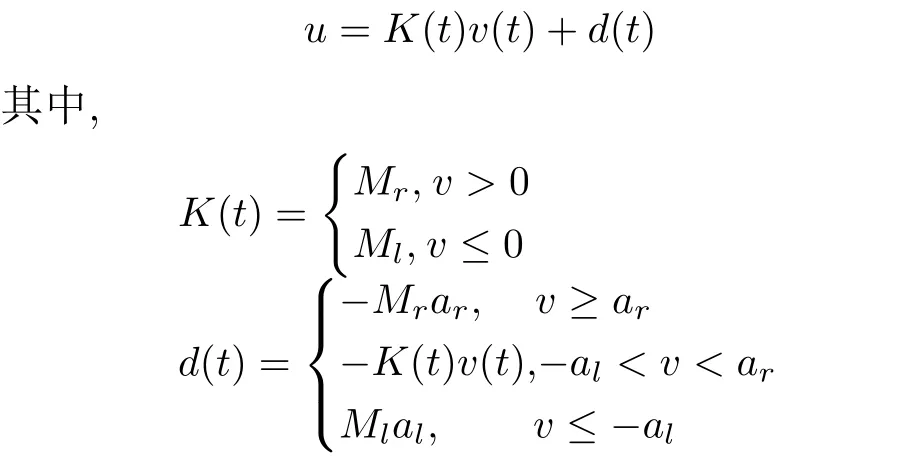
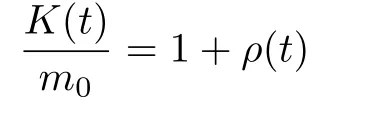
其中,ρ(t)是分段且有界的函数,满足

根据以上讨论,可得

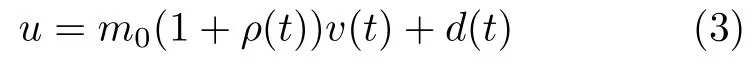
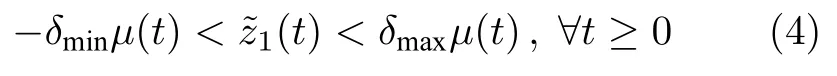
则称系统的暂态性能满足指定性能的要求.其中,δmin,δmax>0 是可调节的参数,指定性能函数取为µ(t)=(µ0−µ∞)e−nt+µ∞,函数µ(t)是严格单调递减的函数,n>0,µ0=µ(0),µ∞=limt→∞µ(t),那么µ0>µ∞>0,而且满足δmaxµ(0).上面不等式可以等价于以下等式

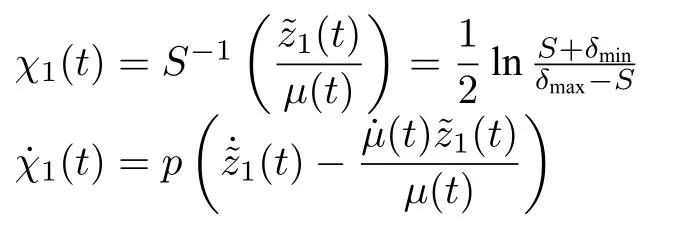
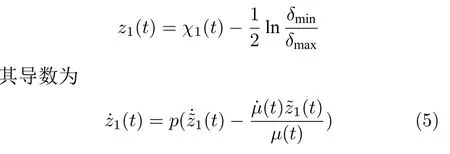
本论文的控制目的:针对一类考虑指定性能和具有输入死区约束的非线性严格反馈系统设计一种自适应模糊最优控制器,保证闭环系统中所有信号都是一致最终有界的,误差信号收敛到以“0”为中心的邻域内,并且满足指定性能要求,同时代价函数达到最小值.

引理1[19].对任意给定的精度ς >0,都存在模糊逻辑系统wTϕ(Z)能逼近任意连续的非线性函数F(Z), 使得F(Z)=wTϕ(Z)+ϑ(Z), 其中|ϑ(Z)|≤ς,这里F(Z)是定义在紧集 ΩZ ∈Rq上的函数,w是理想权重向量,定义为

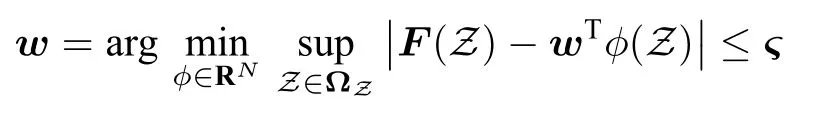
引理2[19](Young's 不等式).对于任意x,y ∈Rn,有以下不等式成立:

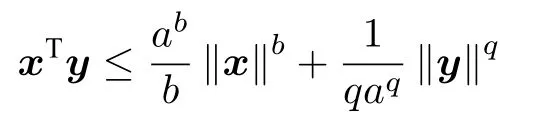
其中,a>0,b>1,q >1且 (b−1)(q−1)=1 .

2 控制器设计

在本节中,首先结合backstepping 方法和命令滤波技术,设计前馈控制器Ua.然后,采用自适应动态规划方法设计出最优反馈控制器U∗.最后,整个控制输入Uw=Ua+U∗.

2.1 前馈控制器设计

首先进行如下坐标变换

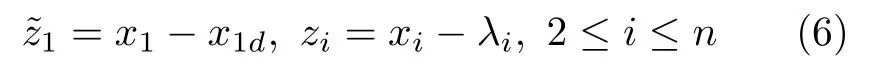
其中,x1d为参考信号,λi是虚拟控制输入xid通过一阶命令滤波器的输出.是前馈虚拟控制输入,为最优反馈虚拟控制输入.最后一步中定义v=va+v∗,va为前馈实际控制输入,v∗为最优反馈实际控制输入.一阶命令滤波器表达式为

其中,τi是时间常数.为了消除滤波器误差λi−xid的影响,设计误差补偿信号ζi(2≤i ≤n−1)为

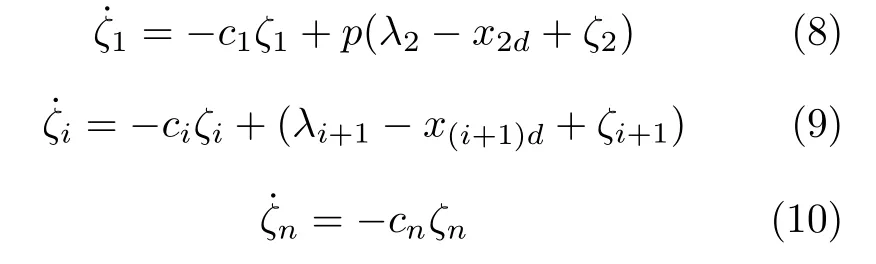
其中,ci >0是设计参数,ζ(0)=0 .

定义补偿跟踪误差为

结合式(5)∼(11),对求导可得

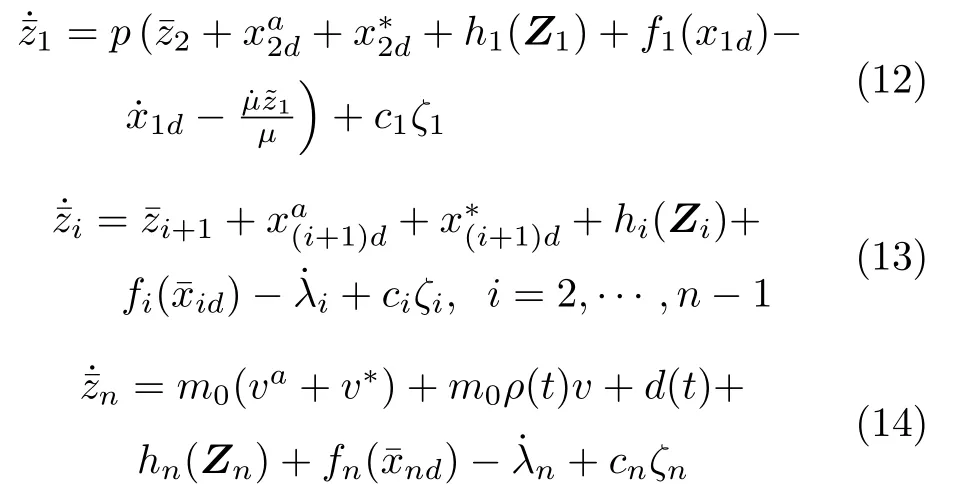
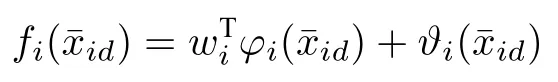
第1步:考虑如下Lyapunov 函数

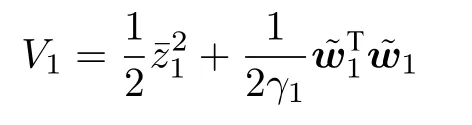
设计前馈虚拟控制器和自适应律如下:

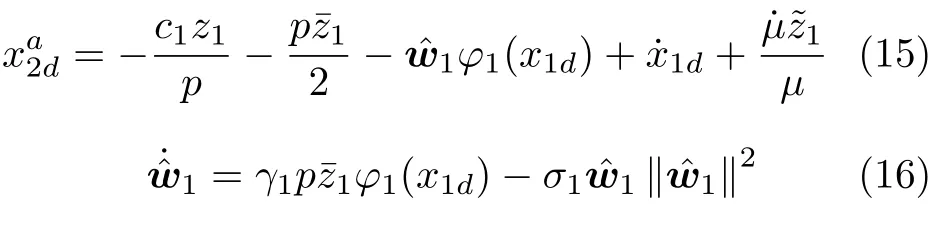
根据式(15)和式(16),对V1求导有

第i步(2≤i ≤n−1):考虑如下Lyapunov 函数

设计前馈虚拟控制器和自适应律如下:

根据式(17)∼(19),对Vi求导有

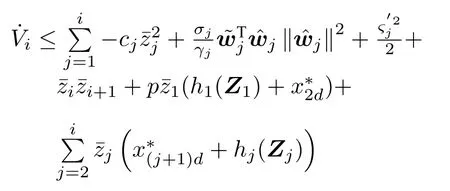
第n步:考虑如下Lyapunov 函数

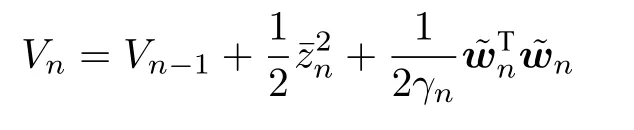
设计前馈控制器va和自适应律如下:

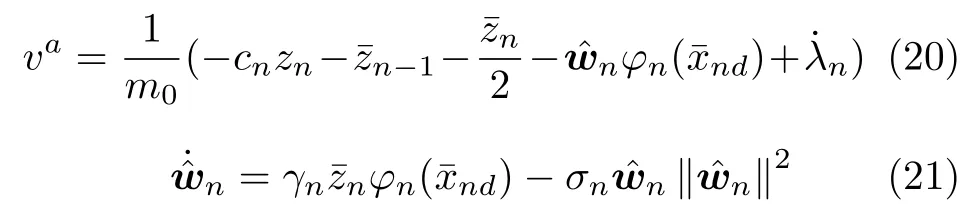
根据式(20)和式(21),对Vn求导有

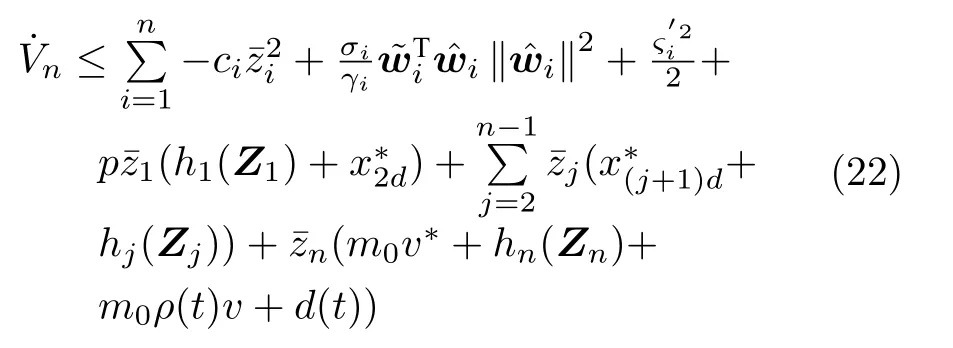
根据Young's 不等式,对式(22)不等式右边第2、6 项变换如下

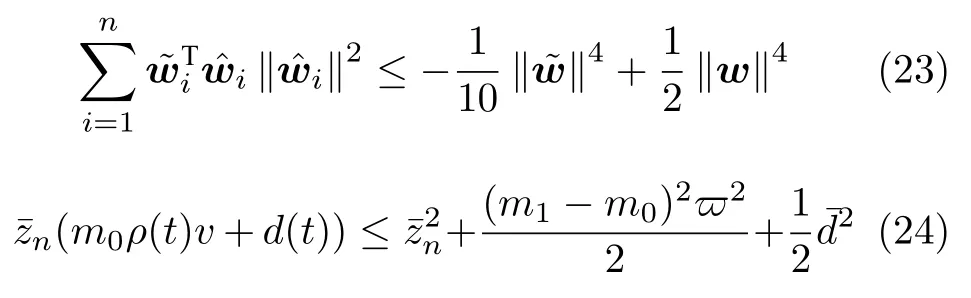
将式(23)和式(24)代入式(22),可得

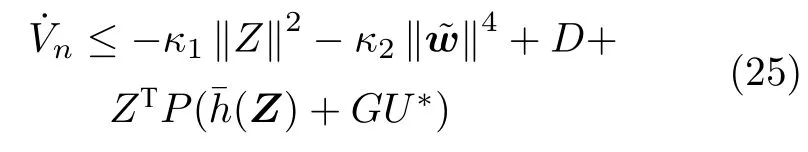
如前所述,系统(1)的控制输入Uw=[x2d,...,xnd,v]T由两部分Ua和U∗构成,前馈控制器的表达式如式(15),(17),(18),(20)所示.由式(25)可知,前馈控制器Ua不能保证整个闭环系统的稳定性.因此,需要设计最优反馈控制器使得Uw能够保证被控系统(1)稳定.

2.2 最优反馈控制器设计

本节中,设计最优反馈控制器U∗使如下误差仿射系统稳定,并且使得代价函数达到最小.

定义系统(26)的代价函数为

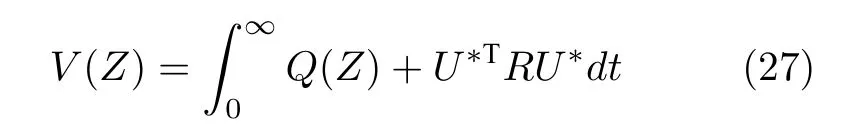
其中,Q(Z)是半正定的罚函数,R=RT>0 .

根据代价函数(27),定义哈密顿函数如下

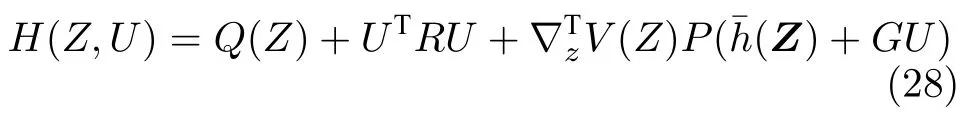
其中,∇zV(Z)是V(Z)对Z的偏导,通过求解=0,解得最优控制输入

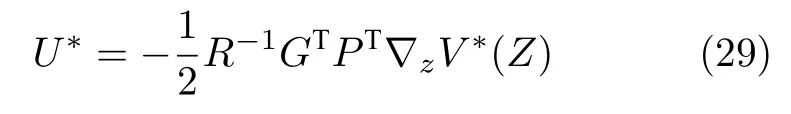
将式(29)代入式(28)可得最优控制输入的充分必要条件:此时哈密顿函数最小.其中,E=PGR−1GTPT,且V∗(0)=0.

引理3[27].对于系统(26),代价函数(27),最优控制器(29),存在径向无界且连续可导的Lyapunov 函数J(Zs),J(Z),使得其中此外, Λ(Z)>0 是一个半正定函数矩阵,满足当∥Z∥=0,有∥Λ(Z)∥=0;当ℓmin≤∥Z∥≤ℓmax,有Λmin≤∥Λ(Z)∥≤Λmax,ℓmin,ℓmax,Λmin,Λmax都是正常数; limZ→∞Λ(Z)=∞,同时使等式Q(Z)+U∗TRU∗=(Z)Λ(Z)成立,其中,那么可得

根据引理1,利用模糊逻辑系统逼近最优代价函数,可得

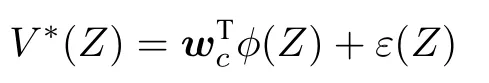
其中,wc为理想的权值,ϕ(Z)为模糊基函数,ε(Z)为逼近误差.则最优代价函数的梯度为

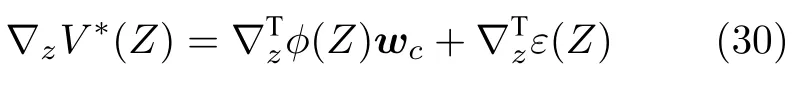
将式(30)分别代入式(28),(29)可得

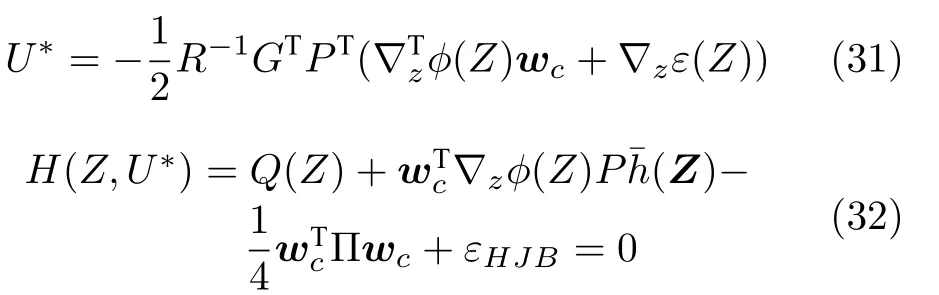
利用模糊逻辑系统对代价函数进行估计,则有

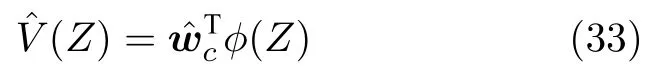
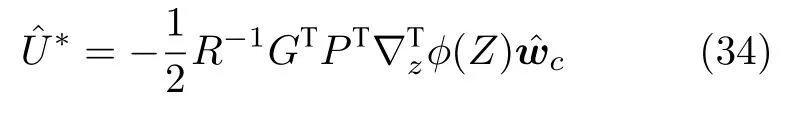
将式(34)代入式(28),得到哈密顿函数的估计为

为使 最小,利用梯度下降法设计得

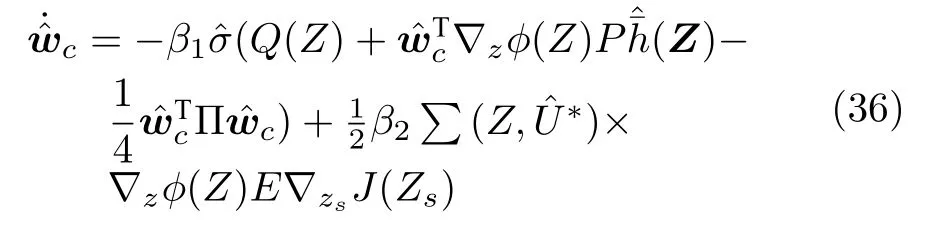
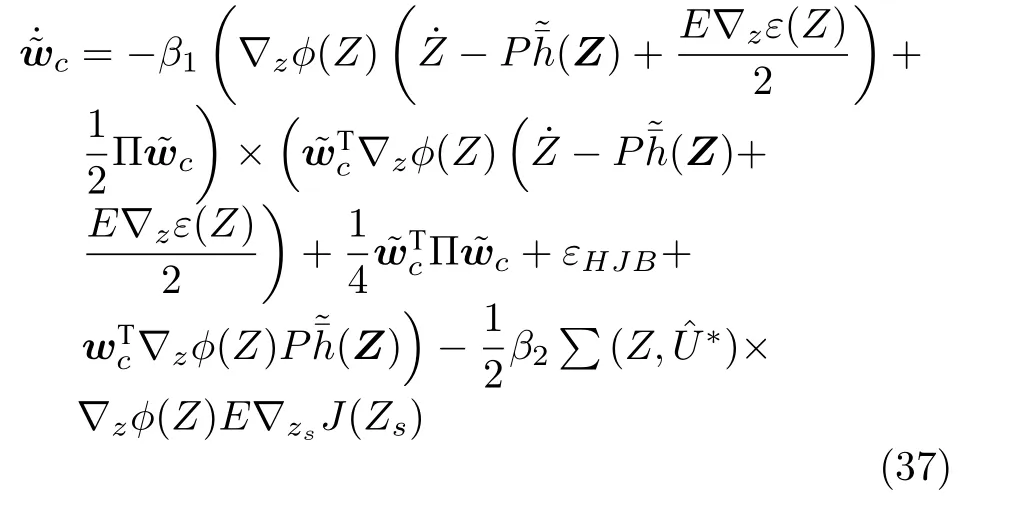
根据自适应律(16),(19),(21),引入附加项,可得

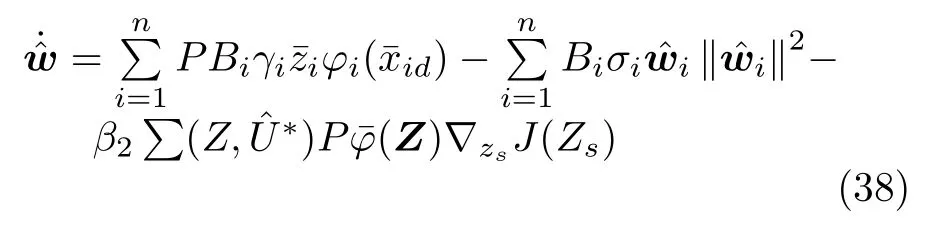
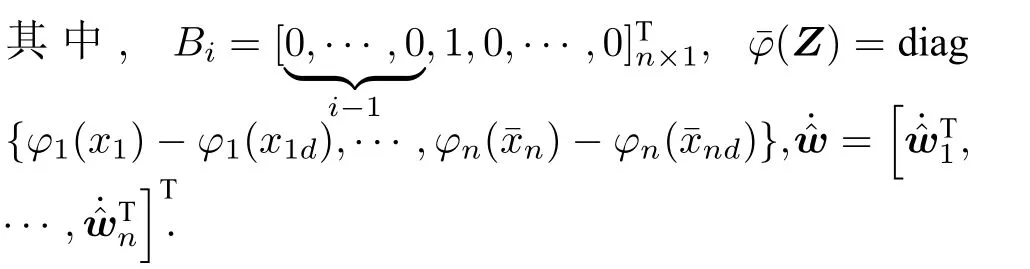
定理1.针对一类考虑指定性能和具有输入死区约束的严格反馈非线性系统(1),设计前馈虚拟控制器(15),(17),(18),前馈实际控制器(20),反馈最优控制器(34)及自适应律(36)和(38),通过选择合适的参数使得闭环系统内所有信号一致最终有界,跟踪误差以最优的方式收敛且满足指定性能要求.

证明.见附录A.

3 实例仿真

本节将通过一类机械臂系统仿真验证所提出自适应模糊最优控制方法的有效性和可行性.带有输入死区约束的机械臂系统动力学方程如下:

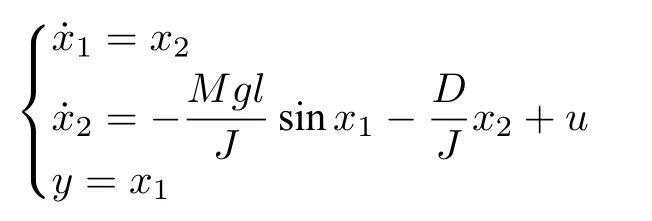
其中,x1,x2分别为连杆角速度和角加速度,M=1 kg为连杆总质量,g=9.8 m/s2为重力加速度,l=1 m 为机械臂连杆的质心距连杆的转动中心的距离,D=2 N·m·s/rad 为连杆转动的粘性摩擦系J=1 kg·m2数,为连杆转动惯量.

参考信号x1d=sin(t).死区参数Mr=3,Ml=1,ar=1.5,al=3.模糊隶属度函数为4,5.初始值为x1(0)=1.4 ,x2(0)=−0.2 .=[1,1,1,−1,−1]T.性能函数µ=2.5e−0.5t+0.05,δmin=0.6,δmax=0.8.设计参数为c1=10,c2=50,γ1=1,γ2=1,σ1=50 ,σ2=50 ,β1=0.01 ,β2=0.01,给定系统代价函数(27)中R=[0.2,0;0,0.01],其余参数初始值均为0.

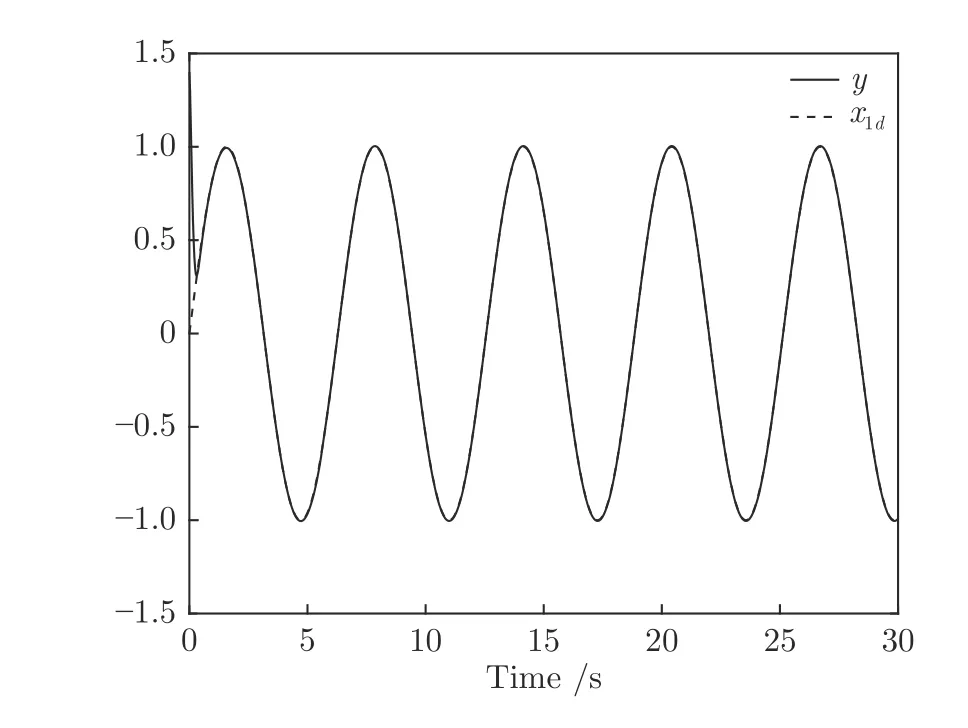
图1 参考信号 x1d和输出信号yFig.1 Reference signal x1d and output y

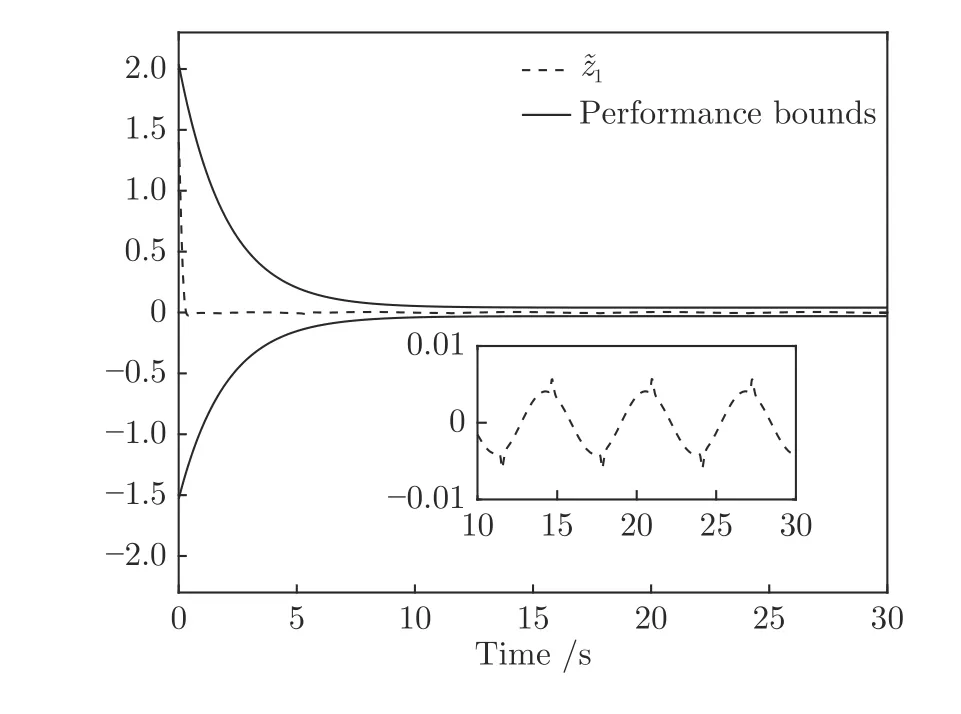
图2 的轨迹和指定性能边界曲线Fig.2 Trajectories of and performance bounds

仿真结果如图1∼4 所示,图1 给出了参考信号x1d和系统输出信号y的跟踪轨迹,系统输出y在5 s 内跟踪上参考信号,表明本文的控制方法能使系统输出具有良好的跟踪效果.图2 给出了跟踪误差的轨迹曲线,由图中可以看出跟踪误差收敛于以原点为中心的有界邻域内,满足预设性能的要求,并且稳态误差小于0.01.图3 给出了代价函数权值和哈密顿函数的估计值的变化曲线,表明权值信号能快速收敛到目标权值并使得哈密顿函数趋于0.图4 描绘了执行器输入信号v和执行器输出信号u的响应曲线.由仿真结果可知本文提出的控制方案使得闭环系统内所有信号都是有界的,保证了系统的稳定性.

图3 代价函数权值?和哈密顿函数?的轨迹(i=1,2,3,4,5)Fig.3 Thetrajectoriesof cost functions weights wˆci andHamiltonian ?(Z,?)(i=1,2,3,4,5)

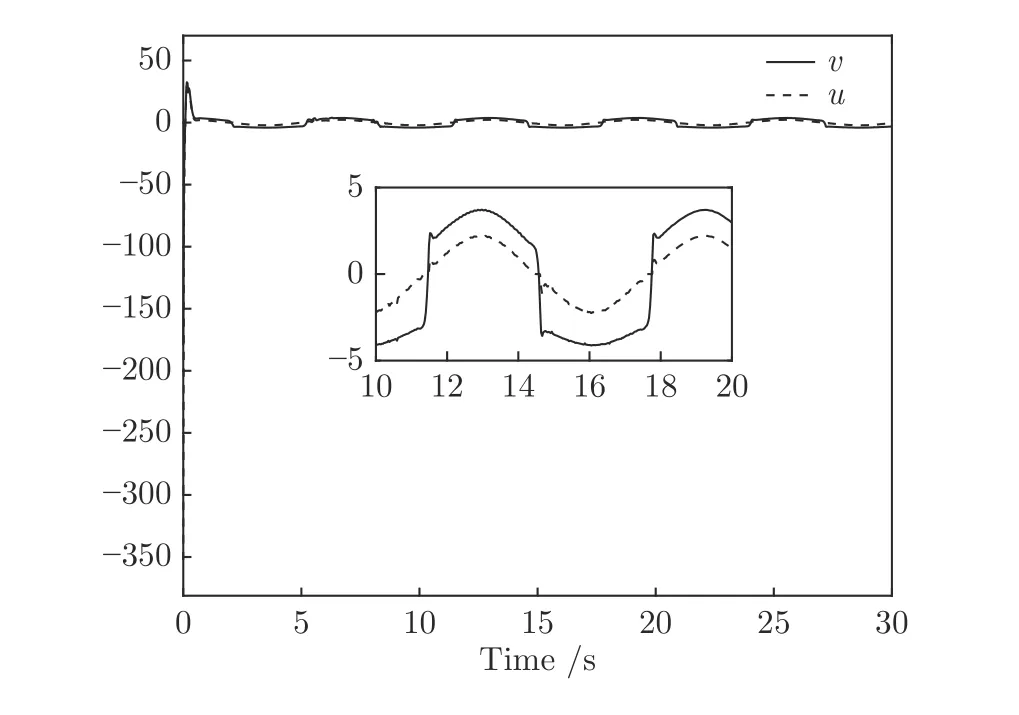
图4 执行器输入信号 v 和执行器输出信号uFig.4 Trajectories of actuator input v and actuator output u

4 结束语

本文针对一类参数未知的严格反馈非线性系统,考虑输入死区和指定性能两个约束条件,提出了一种自适应模糊最优控制方法.首先在backstepping 方法和命令滤波技术的基础上,利用死区斜率信息和性能指标函数设计了前馈控制器.进而采用单网络的ADP 方法,设计了最优反馈控制器.最后采用Lyapunov 函数稳定性理论证明了闭环系统的稳定性.仿真结果表明了本文设计方法能够有效解决考虑死区和指定性能的严格反馈系统的优化控制问题.

附录A

选取Lyapunov 函数为