北江大堤的瞬态渗流分析与减压井防渗效果模拟

徐文兵, 姚清河, 王生，伍明兆

(中山大学航空航天学院，广东 广州 510006)

堤防工程是防洪工程体系的重要基础，是抵御洪水的重要屏障[1]。我国的堤防工程一直缺乏应有的重视和研究，存在着堤身质量差、防渗能力差、缺乏有效的监测手段等众多问题，而在所有安全问题中，渗流破坏是堤防工程最主要的、最常见的问题[2-3]。1998年长江发生特大洪水，长江中下游渗透险情达65 100处，占总险情的88%。而在7处较大的溃口中，有5处都是因为渗透变形发展成渗透破坏，最终导致堤基溃决[4]。近两年来，“山竹”、“天鸽”等极端恶劣天气的到来使得堤防水位骤升，加剧了许多堤防工程的渗流破坏。堤坝渗流问题频频发生，堤防工程渗流分析成为当下的研究热点之一[5-8]。堤防工程渗流分析方法主要包括模型实验、数值模拟、资料分析[4]。模型实验往往需要耗费大量的人力物力、成本高昂，而且受实验条件限制，难以对各种特殊工况进行全面的研究。资料分析需要进行现场勘测、收集大量监测数据，往往需要很高的经济成本。而数值模拟成本较低、精度较高、可模拟多种工况，给予适当条件能获得精度较高的结果。因此，目前相关研究普遍采用数值模拟的手段进行分析。众多学者通过有限元分析(FEM)方法对堤防工程的渗流问题进行了数值模拟。Zienkiewiz[9]等首先应用有限元法对饱和孔隙介质中不可压缩流体的恒定流进行了分析，提出了有限元适用于所有按变分形式计算的场问题的观点。张家发等[10]针对长江中下游堤防工程现状概化出典型条件，采用有限元数值模拟方法对堤身堤基渗流场进行了模拟计算，分析了作用水头、堤身渗透性、弱透水覆盖层厚度、分别隐伏于覆盖层下和出露于地表的强透水层的厚度、外滩宽度和河流切割程度等因素对堤身堤基渗流规律的影响，总结出一般性规律。Vermee[11-12]利用一种数值模拟与可靠度分析耦合的自适应响应面的一阶可靠度法来分析瞬态渗流，考虑了路堤内瞬态渗流对堤防稳定性的影响，分析认为稳定浸润线是堤防稳定的关键。Wu等[13]采用有限元程序COMSOL求解了土坡降雨渗流、变形和稳定性的影响。邱宽红等[14]通过有限元分析软件GeoStudio，结合工程实例对堤防工程稳定流进行了渗透稳定性分析，比较了桩基施工前后的渗流特性。

在减压井防渗效果研究方面，张挺和詹杰民等[15]通过实测资料分析和稳态渗流场模拟计算,分析了北江大堤各种防渗措施的功效,认为防渗减压工程对本堤段防渗是有效的,并对大堤的防渗安全进行了评价,为堤防的防渗建设提供了参考。李景娟等[16]在稳态渗流的基础上对减压井贯入深度、井管直径、井间距、出水口高程以及滤层透水性等因素进行了二维渗流有限元计算。综上所述，目前减压井的模拟分析大部分是基于稳态渗流场；有关“山竹”、“天鸽”等极端天气水位暴涨情况下减压井防渗效果的变化鲜有报道。

1 渗流基本方程

根据达西定律，多孔介质的渗流方程可表达为[17]：

(1)

v=kJ

(2)

式中，Q为渗流量；k为渗透系数；A为渗流截面面积；J为渗流的水力坡度；H为总水头；s为水头损失；v为渗流模型的断面平均流速。

Richard于1931年将达西定律推广到非饱和渗流中，得出了非饱和渗流的基本微分方程：

(3)

式中，Kx、Ky、Kz为沿x、y、z方向上的渗透系数；Q1为单元体的边界流量；θ为单元体积含水量；t为时间。当x、y、z三个方向的渗透系数不变，单元体不受外界降雨与蒸发时，即没有外界流入量与流出量，可得：

(4)

当单元体处于各向同性渗流场时，即Kx=Ky=Kz时，(4)式则变为：

(5)

2 计算实例

2.1 模型建立

采用渗流有限元分析(FEM)方法，针对北江大堤石角坝段8+230断面进行建模分析。该坝段高程为17.85 m，模型截面总长度181 m，堤顶宽8.0 m，迎水坡坡比1∶3，原路面以上背水坡坡比1∶3，原路面以下背水坡坡比1∶38。石角段大堤建在厚约15～25 m的强透水层上。堤防横断面近似为梯形，堤身材料包括粉土、粘土、淤质粘土和人工填土等。堤基上层材料为粘土，下层为强透水层，主要包括细砂层、中粗砂层、卵砾石层，模型示意图见图1。假定同一区域内土体的渗透性均一，为各向同性介质[18-20]，相关地质参数见表1。

1985年，国务院批准将厦门经济特区范围扩大到全岛。这年夏天，习近平从河北南下赴厦履新，担任市委常委、常务副市长。

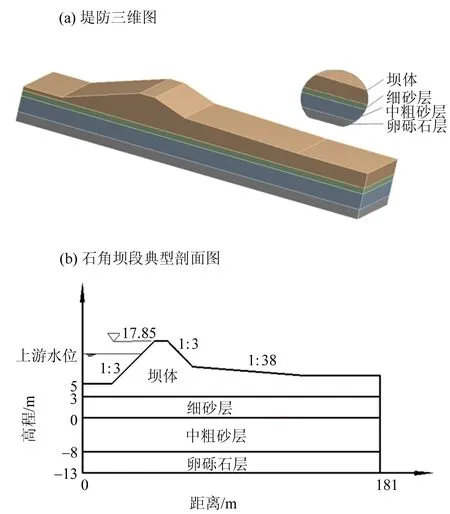
图1 堤防示意图Fig.1 Schematic diagram of embankment

表1 模型渗透系数表Table 1 Model permeability coefficient table (cm·s-1)

2.2 网格独立性验证

对于数值模拟，需要确定计算所用网格的网格数量与计算获得的结果之间的独立性，也就是要进行网格无关性验证。设外江水位为11.38 m，网格全局单元尺寸为0.7、1、1.3 m进行验证。

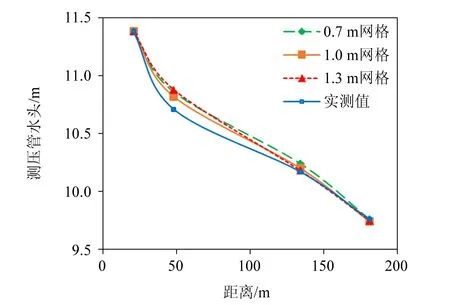
图2 网格独立性验证 Fig.2 Grid independence validation

从图2中可以看出，三种不同网格计算出的测压管水头值曲线几乎重合，可认为单元尺寸为1 m时的网格已达到网格无关，因此我们选择单元尺寸为1 m的网格进行数值模拟。

2.3 有效性验证

将数值模拟的浸润线水头值与四种工况下实际测量所得的测压管水头值进行对比，进行有效性验证。已知三根测压管在外江水位为8.7、9.54、10.56、11.38 m的工况下的测压管水头，测压管分别布置在水平距离48、134、181 m处，水头实测值如表2所示。

数值模拟的边界条件为上游为外江水位，下游为B3测压管的实测值。模拟后的结果如图3所示。把数值模拟数据与测压管实际值进行对比分析，图4为外江水位8.7和11.38 m工况下模拟得出的水头值、测压管实际测量水头值。

表2 8+232测压管水位实测值Table 2 Measured water level of 8+232 piezometric pipe m

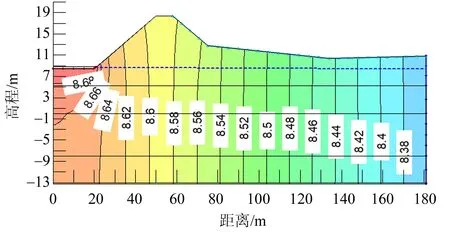
图3 外江水位为8.7 m时的模拟结果Fig.3 Numerical simulation results when the water level of the outer river is 8.7 m

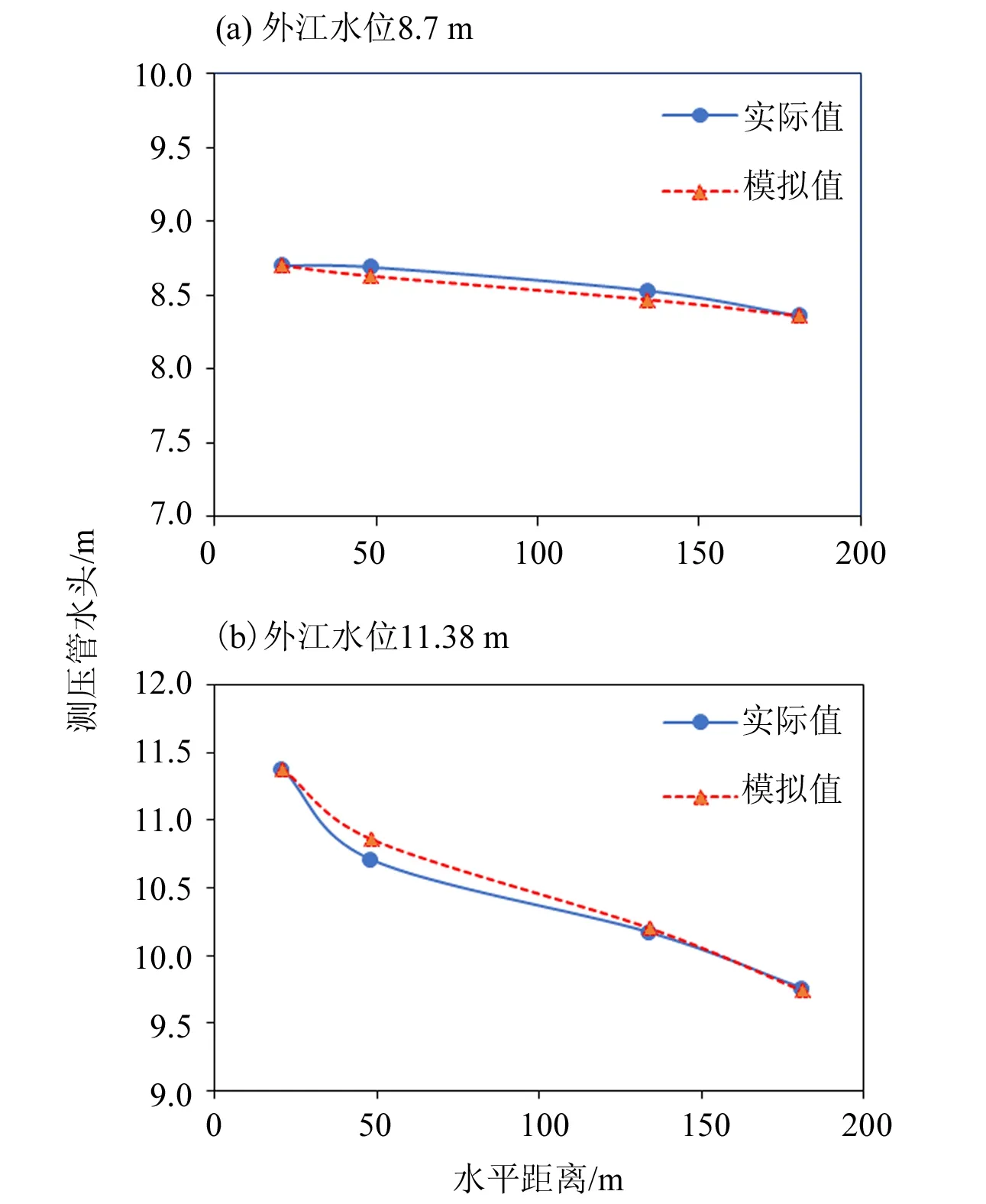
图4 计算水头值与实测水头值对比图Fig.4 Comparison between calculated head value and measured head value

从图中可以看出，模拟得到的测压管理论值与实际测量值十分接近，最大误差不超过0.32 m，最小误差为0，平均误差为0.104 m。总体来说，模拟数值比实测值偏大，模拟结果更为保守、安全，表明建立的数值模拟模型十分贴近提防实际状况。

3 计算结果分析

通过数值模拟我们可以对稳态、瞬态、加了减压井防渗措施的各种堤防状况进行分析，其中主要包括浸润线、渗流量、坡降等方面。外江水位(上游水位)边界条件如图5所示。

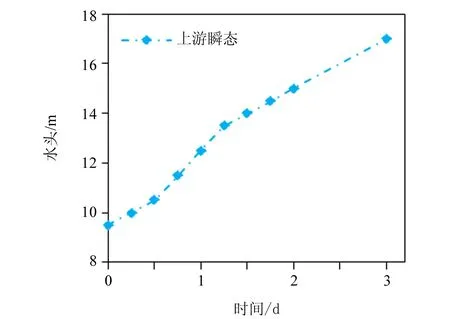
图5 瞬态时上游水位的边界条件Fig.5 Boundary conditions of transient upstream water level

3.1 瞬态渗流分析

在实际工程中，堤防失事最大的原因就是由于渗流破坏引起的。在坝体及坝基中的渗流作用下，由于其机械或化学作用，使土体颗粒流失、产生局部破坏的变形(如管涌或流土等)。水的渗流作用会使土体饱和度增加，非饱和区域的基质吸力降低，从而增加边坡失稳的可能。特别是在水位变化的情况时，坝体内由于水位突然的升降，会使土体内存在着较大的渗流应力，从而更容易造成边坡土体的破坏。所以，对堤防的瞬态分析能够比较好的预测堤防出现破坏时的水位，对堤防的安全运行具有很强的指导意义。

图6为瞬态时浸润线的变化曲线。从图中可以看出，随着水位的升高浸润线变化越来越大，坝段面等势线值增大，最高水位时最低等势线值达到11。当外江水位在15 m左右时，浸润线过原路面以上背水坡坡脚，随着雨量的增加此处将会容易发生管涌、流土等现象。

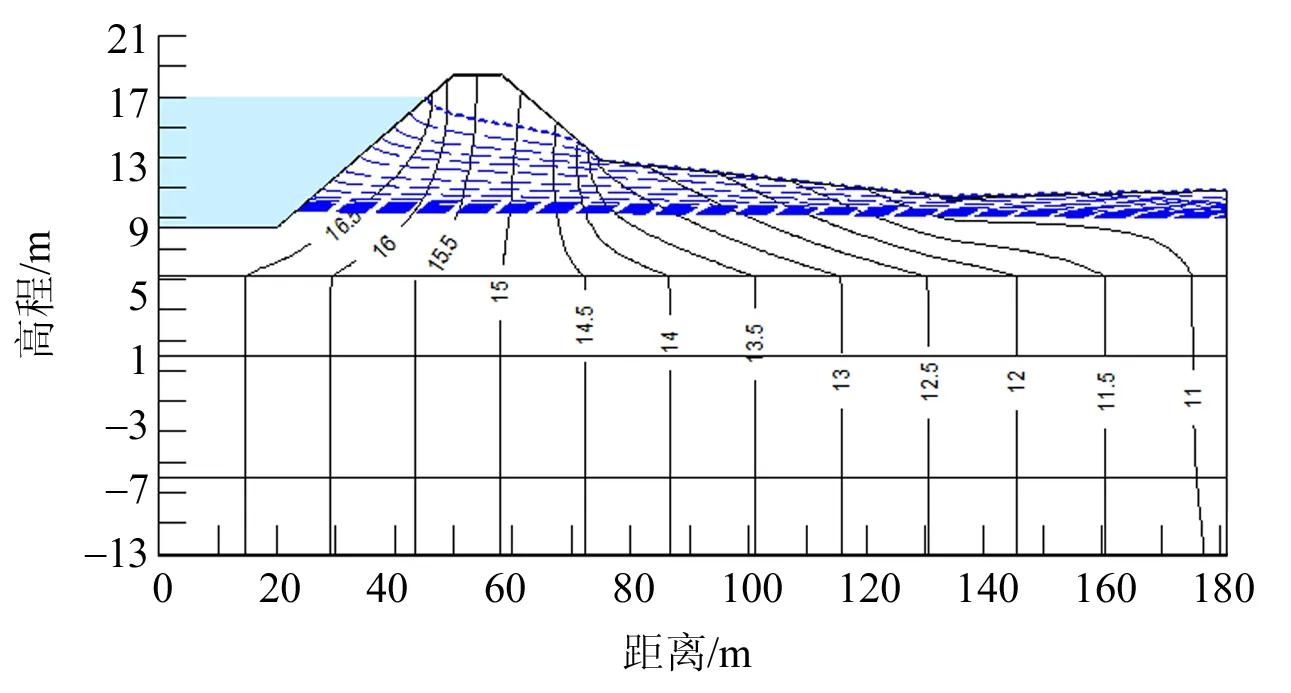
图6 瞬态时浸润线的变化曲线Fig.6 Change curve of phreatic line in transient state

图7-8中，同等水位下瞬态的渗流量要比稳态渗流量大，渗流量最大达到9.43×10-5m3/d，同等水位下降雨时应做出更高的安全措施。随着水位的增长，坝体渗流量也逐渐变大，坝体的坡降也呈曲线增加。当水位在15.78 m时，得出坡降达到0.5堤防发生破坏[21]；为了增加堤防的安全性，我们对堤防加入减压井防渗措施。

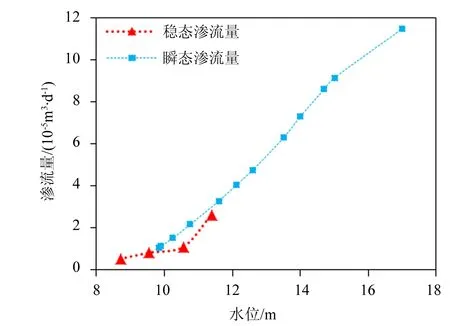
图7 瞬态、稳态流量变化图Fig.7 Changes in transient and steady-state seepage quantity

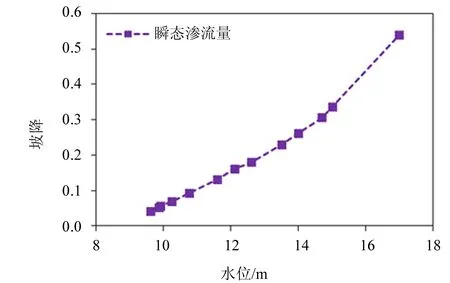
图8 瞬态坡降变化图Fig.8 Changes in transient seepage water grade

3.2 减压井渗流分析

减压井作为主要的渗流控制手段之一，在堤防工程中受到广泛使用。减压井常在堤防、大坝等工程中使用。如果设计、施工不合理或运行管理不善会造成出水量小,减压效果差,危及堤防安全。因此，对减压井的位置及贯入深度研究具有重要意义。本文主要对不同深度、不同位置的减压井进行分析。减压井深度设为10、11、12.5、16.5 m四种类型，水平距离设为84、94、114 m处设置贯入深度为12.5 m。

随着外江水位的变高，浸润线高度也升高，溃堤危险就越大。如图9所示，当减压井深入强透水层时浸润线高程明显降低(降低高程为8～12 m之间)，大量的水在减压井处被排出，防止发生管涌与流土、沼泽化等现象。减压井左边的等势线值几乎变为0，可见减压井的作用显著。

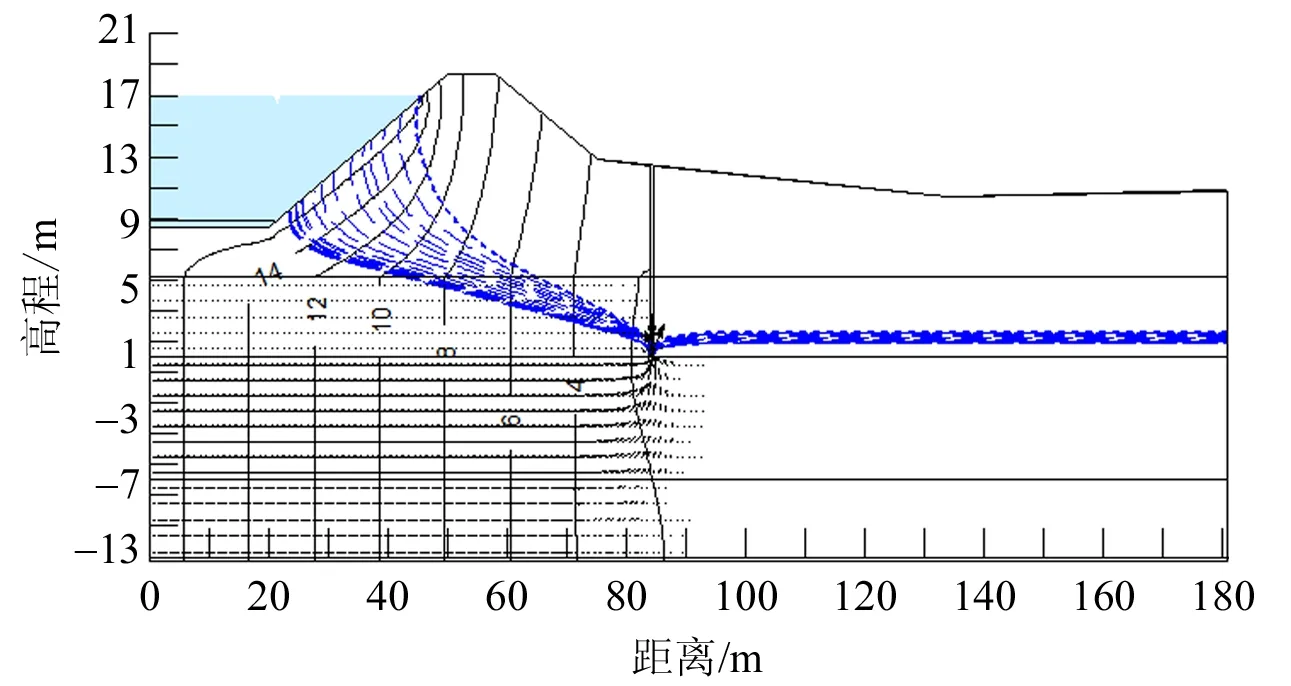
图9 加减压井数值模拟浸润线变化Fig.9 Variation diagram of phreatic line in numerical simulation of pressure relief wells

如图9(a)所示，减压井排水减压效果受贯入深度影响较大，随着贯入深度的增加，效果逐渐提升;贯入深度由9 m增至11 m时排水减压效果提升相对较小，这2处分别位于细砂层3/5与4/5深度，说明同一渗透系数土层内，贯入深度至该土层3/5～4/5深度范围内较为合理。如图9(a)所示，四种减压井随着水位的增加渗流量也逐渐增加，可见减压井深度为16.5 m对堤防的防渗效果最佳，最佳渗流量为4.51×10-10m3/d。与不加减压井时渗透量为10-5m3/d相比，防渗效果显著。可见，如不考虑经济、技术等综合因素，在不同渗透系数土层减压井贯入深度越深越好。

如图9(b)，我们将深度为12.5 m的减压井放在水平距离为84、95、114 m处，渗流量各不相同，相差近10倍。可见，由于地质条件的不同，同样的减压井放在不同的位置效果差距很大。水平距离为95 m时的防渗效果最好，最小的渗流量2.37×10-10m3/d。

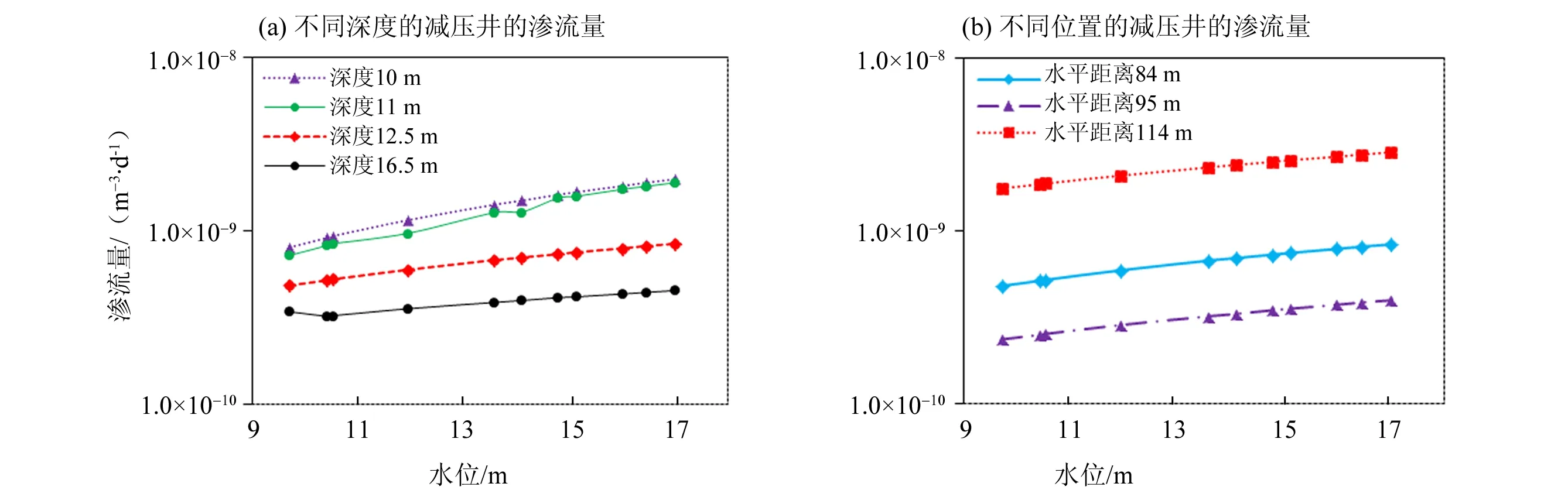
图10 加减压井后的渗流量曲线 Fig.10 Seepage quantity curve after adding relief wells

4 总 结

堤防基础地质变化大，地形复杂，许多数据不易观测。本文通过数值模拟计算了堤防瞬态的渗流场，并选择了合适的减压井防渗措施。最后，针对不同的防渗方案进行了分析。研究结果为：

(1)模型的平均误差为0.104 m，贴近提防实际状况。因此，可以准确、有效的对渗流场进行数值模拟，得到坡降、浸润线及渗透流速情况。水位为15.78 m时，得出坡降达到0.5堤防发生破坏。

(2)在同等水位下，瞬态比稳态渗流量更大。加减压井作为防渗措施后效果显著。与未加减压井时相比，渗流量相差很大。

(3)加减压井后最佳渗流量为8.4×10-10m3/d。浸润线水头降低最高达12 m，渗流量减小有利于防止堤防发生管涌与流土、沼泽化等现象。

致谢：文中北江大堤的地形、地质、水文资料均出自于广东省北江大堤管理局，特此致谢！