基于Xilinx FPGA SRL16E实现最优Half-band插值滤波器*
张 繁
(上海诺基亚贝尔股份有限公司,江苏 南京 210037)
0 引 言
数字滤波器的设计与实现在无线通信数字信号领域有着广泛的应用。我们在学习和研究数字滤波器的原理和设计的同时,在FPGA中实现高效而又省资源的数字滤波器,对工程实现有着十分重要的意义。
1 数字滤波器简介
1.1 数字滤波原理
数字滤波器是对数字信号实现滤波的线性时不变离散系统。它的实质是一个运算过程,即输入的数字信号序列通过特定的运算转变为输出的数字序列。时域上两个序列的线性卷积相当于在频域上其相应的频谱序列的乘积。滤波从本质上来说,就是滤波器冲激响应的傅里叶变换所得到信号频谱的乘积。
1.2 FIR滤波器
2 半带插值滤波器原理
插值是在保持信号频谱内容不变的情况下提高信号采样率。插值的第一步是在每个有效的输入采样之间插入L-1个零值采样点,从而把采样率提高L倍。这使得原始信号的频谱延拓L-1次,这个过程即为“采样率扩展”。插值之后,频域上信号频谱的形状不变。最后将插入零采样值的输入流通过低通滤波器,滤波器的通带位于原始信号频谱位置,滤波器输出所有延拓频谱。
半带(half-band)插值滤波器是一种特殊的低通FIR数字滤波器,通带和阻带关于二分之一Nyquist频率对称,因为有近一半的滤波器系数为0,用来实现数字滤波可以大幅度减少运算量,有利于滤波器的实时实现。图1为脉冲响应,图2为多相划分。图3为充分利用系数数据中0项的优化体系结构。
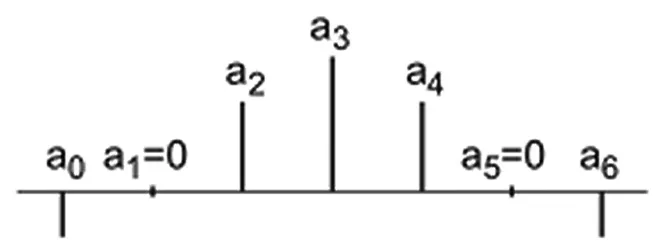
图1 脉冲响应
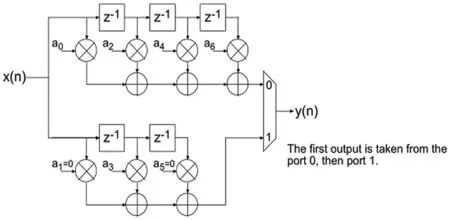
图2 多相划分

图3 对0项优化后的半带插值滤波器结构
3 Xilinx FPGA SRL16E用法介绍
3.1 SRL16E基本结构
SRL16E实际上是查找表LUT的另一种操作模式,如图4所示。
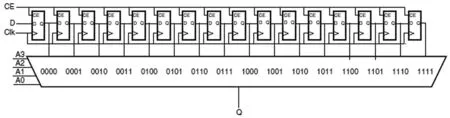
图4 SRL16E 基本结构
16个配置单元被组织成一个移位寄存器连接到多路复用器(multiplexer)。多路复用器根据A[3:0]从16个单元中选择一个作为输出。
3.2 FIR Filter用法
众所周知,Xilinx FPGA SRL最基本的用法就是用于移位寄存器或data delay。如果一个数据要delay 10个周期,那么如果用寄存器打拍法需要打10拍,即需要10个D触发器,需要占用5个Slice。而如果使用SRL16E来实现,不仅用法简单,而且只需要占用一个SLICEM。而这里我们要运用的是它的另一种advanced场景:FIR Filter application。如图5所示,在这里,SRL16E构成了FIR filter的抽头。
在这种应用下,移位寄存器和多路复用器是完全独立的。在CLK和CE信号的控制下,移位寄存器会从D input读取数据,而Q output则完全取决于A[3:0]的选择。时序如图6所示。
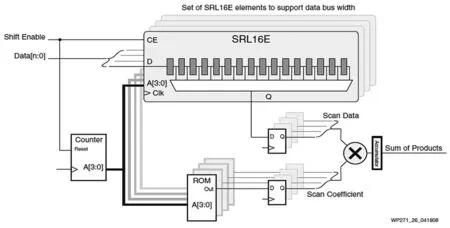
图5 FIR Filter Logic

图6 FIR Filter timing
在该模式下,CE和A[3:0]的值不是固定不变,而是根据设计需要,CE为脉冲,在CE为高时,SRL16E会读取DIN的数据,然后当CE为低后,紧接着根据A[3:0]的值来决定Q输出哪个抽头。如图 6所示,Shift Enable为 CE, Counter为 A[3:0],而Scan Data则为Q输出。
4 基于SRL16E的最优插值滤波器设计与实现
4.1 设计
在本例中,我们对Half-band插值滤波器采用SRL16E FIR Filter及DSP48E来构造。跟往常我们在输入数据处插值不一样,这里先通过滤波器计算出插值数据,根据插值数据特征,再进行2倍插入。可以节省FPGA一半乘法器的资源。
我们先假设参数:
Fs = 122.88MHz (output)
Number of taps = 15.
Filter Taps:[c0,0,c1 0,c2 0,c3 m,c3,0,c2,0,c1,0,c0],其中 m =1。
首先按照常规Half-band插值模式进行计算:
①.输入数据为61.44Msps,输入数据为:
d0,d1,d2,d3,d4,d5,d6,d7,d8,d9,d10,d11,d12…
②.对输入数据进行插值得到122.88Msps新输入数据:
d0,0,d1,0,d2,0,d3,0,d4,0,d5,0,d6,0,d7,0,d8,0,d9,0,d10 0,d11,0,d12…
而系数为:
[c0,0,c1,0,c2,0,c3,m,c3,0,c2,0,c1,0,c0]
③.在122.88M数据率下按照如下方式进行卷积计算插值:
如图7所示,输出序列为y0,y1,y2,y3,y4,y5,……
y0=d0*c0+0*0+d1*c1+0*0+d2*c2+0*0+d3*c3+0*m+d4*c3+0*0+d5*c2+0*0+d6*c1+0*0+d7*c0=(d0+d 7)*c0+(d1+d6)*c1+(d2+d5)*c2+(d3+d4)*c3
y1=d3*m=d3
y2=d1*c0+0*0+d2*c1+0*0+d3*c2+0*0+d4*c3+0*m+d5*c3+0*0+d6*c2+0*0+d7*c1+0*0+d8*c0=(d1+d 8)*c0+(d2+d7)*c1+(d3+d6)*c2+(d4+d5)*c3
y3=d4*m=d4
y4=d2*c0+0*0+d3*c1+0*0+d4*c2+0*0+d5*c3+0*m+d6*c3+0*0+d7*c2+0*0+d8*c1+0*0+d9*c0=(d2+d 9)*c0+(d3+d8)*c1+(d4+d7)*c2+(d5+d6)*c3
y5=d5*m=d5
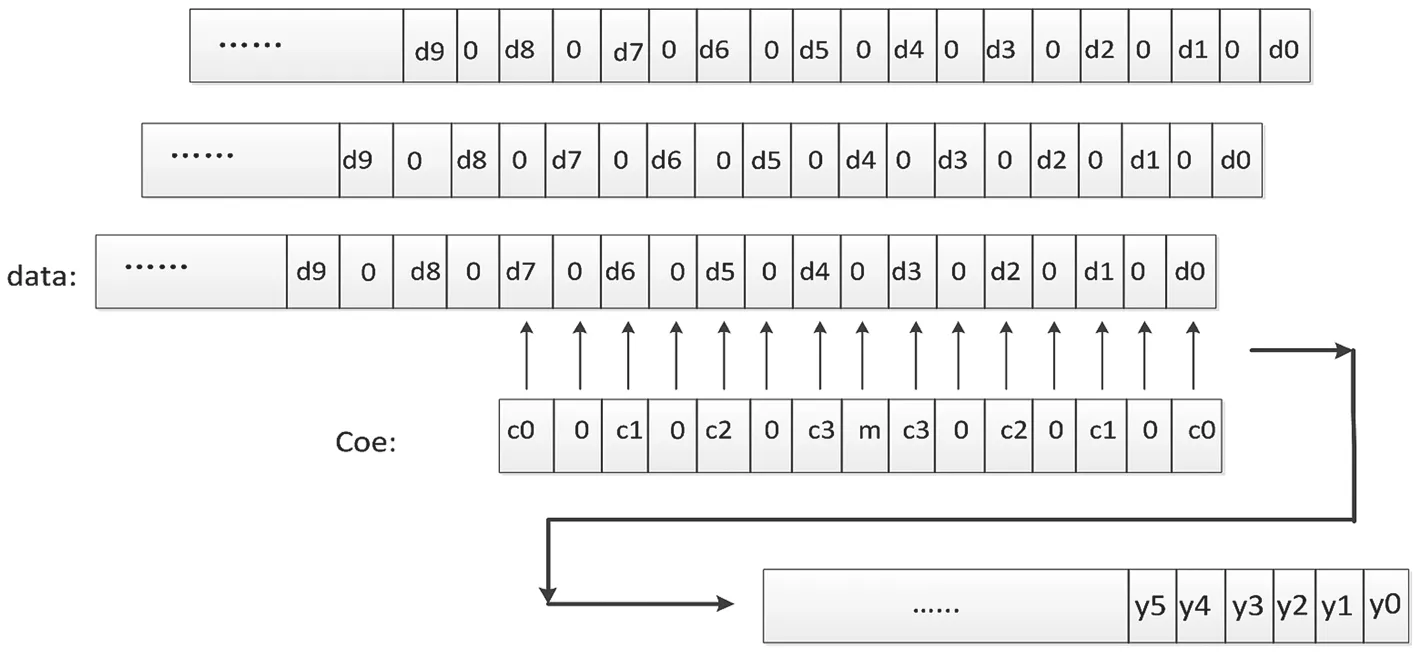
图7 Half-band插值滤波器计算过程
因为系数是对称的,所以FPGA在进行最优化设计实现时采取了如下方法:DSP48E中提供A和D输入进行pre addition。先算出y0,y2,y4,y6,…的插值序列(phase0序列,61.44 Msps数据率),再与y1,y3,y5,y7,……的序列(phase1序列,61.44 Msps数据率)合路,完成最终完整的122.88 Msps的输出序列y0,y1,y2,y3,y4,y5,……。如图8所示。

图8 DSP48E 计算内插值
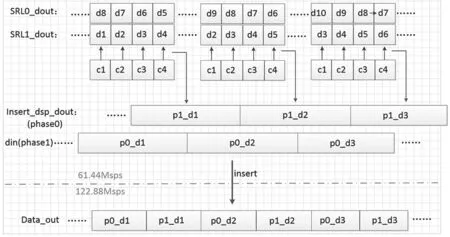
图9 FPGA实现最优Half-band插值过程
插值过程如图9所示。根据FPGA实现最优Half-band插值过程图,我们可以看到,在对半带插值滤波器进行0项优化结构之后,再根据系数对称的特征进行优化处理,还能再进一步节省一半的乘法器资源。
4.2 实现
用Questasim仿真软件对FPGA代码进行仿真。SRL16E_0及SRL16E_1产生的输出分别送给DSP48E的A跟D输入,并计算出插值结果phase0_data(61.44Msps)。仿真结果如图10所示。Phase0与原输入phase1_data(61.44Msps)进行插值,最终得到data_out(122.88Msps),仿真结果如图11所示。

图10 DSP48E仿真结果

图11 插值仿真结果
5 结 语
除了根据系数对称的特点进行优化,在条件允许下,还能对乘法器进行时分复用,以进一步节省乘法器资源,这对于一些资源紧张的FPGA设计来说是一种非常有用的方式。有效利用FPGA的资源结构,抓住设计特点进行FPGA最优化设计对工程实现具有十分重要的意义。

