一种基于双混沌映射的数字图像分块加密方案

伊皮提哈尔·塔依尔，阿布都热合曼·卡的尔

（1.新疆财经大学统计与数据科学学院，乌鲁木齐 830012；2.新疆财经大学信息与管理学院，乌鲁木齐 830012）

0 引言

近年来，随着网络技术的飞速发展，网络交互过程中的信息安全问题备受关注，因此出现了大量了信息保密方案，又因为混沌系统具有初值强敏感性、强随机性等奇特的特性，因此基于混沌理论的保密通信方案开始涌现。例如，薛亚娣等人[1]利用Logistic混沌系统与Henon混沌系统设计了一种基于组合混沌系统的图像加密算法，周一聪等人[2-4]设计了基于新一维混沌系统的图像加密方案，Hua等人[5]设计了一维混沌映射的通用框架，使三种常用的一维映射够两两结合，形成具有更好混沌行为的新映射。李頔等人[6]根据LM-PRNG直接生成随机数数据分布的特性，设计了一种基于直方图优化法的改进Logistic伪随机数发生器（ILMPRNG），Shen等人[7-9]提出基于超混沌系统的加密算法，Xing等人[10]提出了一种基于AES密钥生成调度和混沌映射的灰度图像加密方案，Liu等人[11]提出了一种基于多种常用混沌映射的图像块加密算法，Reddy等人[12]提出了一种利用混沌映射将患者信息嵌入医学x射线图像的方法，保护了患者信息的机密性，并增加了对医学图像的保护，Liang等人[13]提出了一种基于Chebyshev混沌神经网络的视频水印算法。

本文在上述研究的基础上，提出了一种新的基于双混沌映射的图像分块加密方案，其方法是使用两种混沌映射构造伪随机序列发生器，生成二维随机密钥流，通过图像分块的方式，采用“扩散-混淆”两轮加密方式进行加密，得到最终的密文图像。实验结果表明了该算法可以抵抗差分攻击、穷举攻击等各攻击类型，提高了图像信息的安全性。

1 映射描述

1. 1 Chebyshev映射

Chebyshev映射是简单且有效的映射，Chebyshev映射的非线性差分方程如式（1）所示：

其中，w是Chebyshev映射的度，它相应的不变密度如式（2）所示：

Chebyshev映射具备优良的非线性动力学特性，当w∈[2,6]时，该映射的Lyapunov指数为正数，说明该映射是混沌的。Chebyshev映射的分岔图与Lyapunov指数谱如图1所示，当w∈[2,6]时，映射处于混沌状态。

图1 Chebyshev映射的分岔图与Lyapunov指数谱

1. 2 Henon映射

Henon迭代映射如式（3）所示：

其中，a∈[1.1,1.4],b=0.3时，该映射进入混沌状态[2]，Henon映射存在单值确定的逆，其逆映射如式（4）所示：

该映射的分岔图与混沌吸引子图如图2所示。

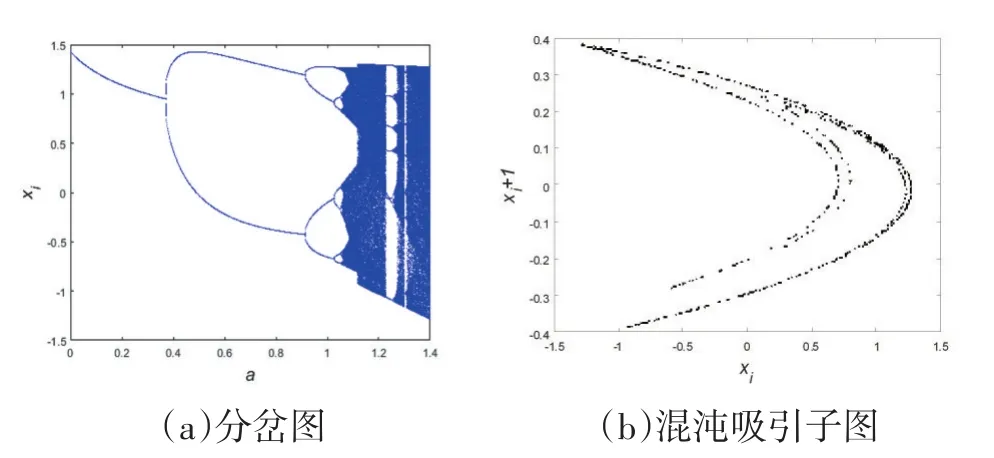
图2 Henon映射分岔图与混沌吸引子图

由此可见Henon映射分岔图呈现倍周期分岔，表明Henon映射存在混沌状态。为满足图像加密的条件，将Henon映射进行取模改造，改造后的Henon映射如式（5）所示。

2 算法描述

2. 1 加密算法

本算法主要分为两步，首先利用切比雪夫映射构造伪随机序列发器，生成密钥流，利用密钥流对明文图像P进行像素位置打乱的置乱加密操作得到密文图像C1，其次，对图像进行预处理，将图像分为上部与下部两个分块，然后利用厄农混沌映射对图像块分别进行扩散处理，得到最终密文图像C。

基于双混沌映射的数字图像分块加密方案的算法流程图如3所示，具体步骤如下：

Step 1输入原始图像P，该图像的大小为M×N，本文中M和N均为256，该明文图像为灰度图像。

Step 2利用Chebyshev映射构造伪随机序列发生器 ，参 数 设 置 为u1=4，x0=0.100001，u2=2，y0=0.300001，通过M×N次的迭代得到二维随机矩阵，生成密钥流 Kc，Kc如式（6）所示：

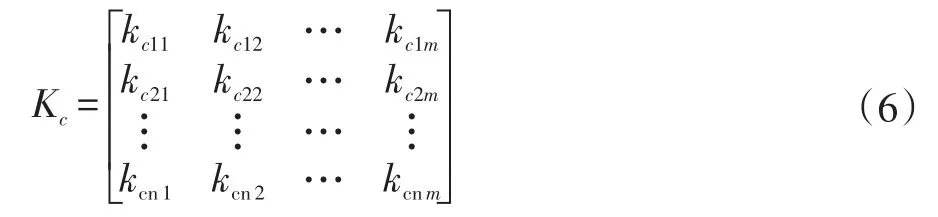
Step 3将二维伪随机序列矩阵作为密钥流，通过明文图像像素与Kc(m,n)的映射关系进行置乱，将明文图像像素作为元素单位，对行内每一个元素按照Kc的排列方式进行排列，从而实现对原有图像像素位置的打乱，实现加密第一步，得到密文图像C1。

Step 4对密文图像C1进行图像预处理，将图像分为上、下部两个子块，得到两个图像块，分为别C1u和C1d，图像大小如式（7）所示。

Step 5利用改造后的Henon映射作为扩散加密函数，其中参数设置为 a=5，b=0.8，d=3，x0=1，y0=3，构造序列发生器，产生两个长度为M×N/2的混沌序列，记为X(i),Y(j)。

Step 6利用 X（i），和 Y（j）对图像上部与下部两块分别进行加密，为了增强比特分布的随机特性，第二轮加密使用异或扩散运算，如式（8）所示，得到密文图像C的上部Cu及下部Cd。

Step 7拼装Cu与Cd，得到最终的密文图像C，如式（9）所示。

图3加密算法流程图

2. 2 解密算法

解密算法为加密算法的逆过程，再此不再详细说明，基于双混沌映射的图像分块解密方案的算法流程图如图4所示，具体步骤如下：

Step 1对密文图像C进行分块处理，分为上部和下部两个子块，分别为Cu和Cd。

Step 2将Henon映射对作为解密函数，利用混沌序列对上部和下部两个子块进行异或扩散操作解密，得到上部和下部两块解密图像，即C1u，C1d，随后，拼装C1u和 C1d，得到密文图像 C1。

Step 3利用Chebyshev映射生成二维随机序列矩阵作为解密函数，对加密图像C1进行像素位置置乱的混淆解密操作，得到明文图像P。

图4解密算法流程图

3 仿真实验

3. 1 实验环境

采用电脑配置为Intel Core i5 CPU 2.40GHz，Windows 7，利用MATLAB 2017b实现加密算法程序设计。

3. 2 加密结果

选择大小为512×512的明文灰度图像P，如图5（a）所示。通过本文提出组合映射算法进行加密，得到第一轮Chebyshev混淆加密图像C1，效果如图5（b）所示，第二轮Henon映射扩散加密效果图C如图5（c）所示。比对 5（a）、5（b）、5（c）图可明显看出，密文图像与明文图像大相径庭，一轮加密和二轮加密的加密图像也有重大区别，无法从图像中得到明文图像中的重要信息，表明该算法可以对图像进行有效的加密，并且可以获得理想的加密效果。

图5加密效果

4 性能与安全性分析

4. 1 密钥空间

以本算法实验环境为例，双精度实数精度可达到10-15，本文的密钥为Chebyshev映射与Henon映射的初值选取与参数选择。又因为本算法中采用二维序列作为密钥流，因此包括：

计算可知，本算法密钥空间为10120>>2100，因此密钥空间足够大，可有效抵抗穷举攻击。

4. 2 直方图分析

我们知道，一个好的加密算法是具有强烈的抗统计分析能力的，我们可以通过直方图分析得知算法是否具有抗统计分析能力。由图6可以看出，密文图像与明文图像的直方图截然不同，密文图像直方图分布十分均匀，可看出密文图像的灰度值在[0,255]上的取值概率十分均等，可以得出该算法能够有效抵抗统计分析，因此安全性很高。

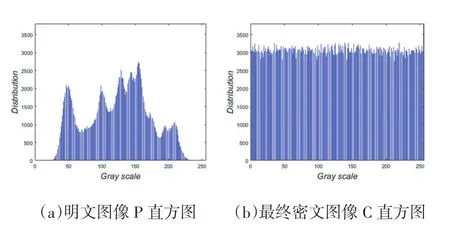
图6直方图

4. 3 敏感性分析

（1）密钥敏感性

密钥敏感性是指当密钥发生微小变化时，加密同一明文图像得到的两个密文图像的差别情况[2]。图7为密钥改变10-15后，加密同一明文图像得到的完全不同地密文图像，由此可以看出，该算法的密钥敏感性较强。

图7密钥敏感性测试

（2）明文敏感性

明文敏感性的测试方法是通过加密算法对明文图像P加密得到加密图像C，随后改动明文图像任意像素的一个比特，得到图像P’，通过加密算法得到加密图像C’，通过对比C与C’计算UACI与NPCR值。

表1为本文算法明文敏感性分析得出的UACI与NPCR值，由表1可以看出，UACI接近理想值与NPCR均接近理想值，因此该算法的明文敏感性较强。

表1明文敏感性分析结果

4. 4 加密速度

由数据验证结果可得，该算法的加密时间为1.737138秒。由此可以看出，该文算法具有加密速度较快的优点。

4. 5 相关系数

一般来说，图像的相邻像素之间存在高度的相关性，因此一些不法分子利用图像信息的这一特点窃取图像中的重要信息，从而达到攻击目的。然而加密算法可以有效地消除图像的相邻像素之间的相关性，达到抗攻击的效果。相关系数的计算公式如式（12）所示。

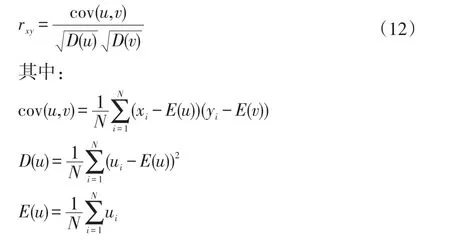
表2为不同算法的相关性系数对比，将本文算法的相关性系数与文献[1]的相关性系数及Logistic混沌系统下的相关系数进行比较。由表可见，明文图像的相关性系数超过0.85，可以看出明文图像的相邻像素间的相关性很强，通过加密算法处理之后，相关系数明显减少，并且，相对文献[2]和Logistic混沌系统下的相关系数，该算法像素间相关性更弱，从而可以得出本算法具有更好的不可确定性与随机性，因此可以获得更好的加密效果。

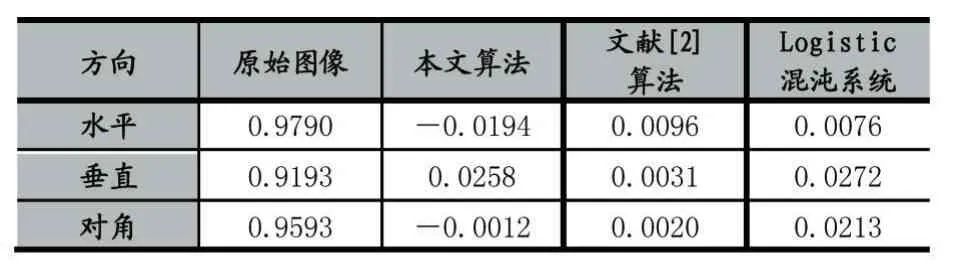
表2不同算法的相关系数比较

4. 6 信息熵

信息熵反映的是图像的不确定性，信息熵越大，不确定性就越大，可视的信息内容就越少，因此就可以判断加密算法的安全性是否较强。信息熵的计算公式如式（13）所示：

表3信息熵

由表3可以看出，明文图像的信息熵与理论有明显差别，并且，密文图像的信息熵接近于理想值，因此该算法的信息熵较大，不确定性较大，加密效果很好。

5 结语

本文提出了一种基于双混沌映射设计数字图像分块加密方案，该算法利用Chebyshev映射构造伪随机序列发生器生成二维序列密钥流，对明文图像进行混淆加密。其次，将密文图像分为上下部两个子块，通过Henon映射分别对两个子块进行扩散加密，子块拼装得到最终密文图像。数据模拟验证，该算法可抵御各类攻击，安全性能较高。具有密钥敏感性强，简单、易实现，加密速度快等优点。