基于可信度方法在严格优势策略中的算法研究
李虎阳,常永虎
(遵义医科大学医学信息工程学院,遵义563000)
0 引言
文献[1]在限定收益的情况下,讨论可信度对重复博弈的影响,要求双方在选择忠诚策略时的总收益大于一个选择忠诚,一个选择背叛时的总收益。但重复博弈更多的是对单次博弈的重复,本文不失一般性地讨论重复博弈,分析了在可信度方法下,参与人能够从严格优势策略中选择其他策略。
囚徒困境是博弈中经典的案例之一,对它的描述如下:警察在案发现场逮捕了两位嫌疑人,但没有足够的证据对他们进行判罚,警察将他们关押在不同的房间进行审讯,以保证他们之间不能沟通。警察分别告诉每个人采取的策略及其收益:如果两个人都坦白,因为证据充分,每个人将会被判处8年的监禁;如果两个人中有一个坦白,一个抵赖,则坦白的会被立刻释放,抵赖的被判处10年监禁;如果两个人都抵赖的话,因为证据不足,每个人将被判处1年监禁。根据以上描述,我们使用二维矩阵表1表示。
如表1所示,参与人A与参与人B的收益一致。以参与人A为例,在单次博弈中,作为理性的参与者,选择“坦白”策略时,其收益分别为-8(B选择坦白)和0(B选择抵赖)总是大于A选择“抵赖”的收益-10(B选择坦白)和-1(B选择抵赖),同理于参与者B,因此最后两个参与人都会选择“坦白”策略,且(坦白,坦白)是该博弈的Nash均衡点,但实际上(抵赖,抵赖)能够使两个参与人的收益最大,该案例说明个人最优策略并不会导致集体最优。

表1
但如果多次进行上述博弈的话,结果可能不太一样。在重复博弈中,每个参与人都能够知道其他参与人的历史策略,因此会根据其他参与人的历史策略,在下轮博弈中,惩罚或者奖励其他参与人,最终可能会打破单次博弈的均衡,获取全局最优。
可信度是对人或者事物的信任程度,其往往由经验或历史行动策略决定。在实际生活中,参与人对于惩罚和奖励总是不对称的,当发现其他参与人选择背叛时,往往会选择比较严厉的惩罚策略,并迅速降低其可信度,但其他参与人选择忠诚时,并不能迅速提高其可信度。
1 博弈与可信度
1. 1 博弈
定义1:博弈(Game Theory)是指参与人在一定的条件下,采取规则允许的行动策略,并从中获得相应收益的过程,可以用一个三元组表示:
G={P,S,U}
其中P是参与者集合,P中的每一个元素表示一位参与者;S是行动策略集合,每个参与者可供选择的策略集;U是收益集合,表示在博弈中,所有参与者在选择某个行动策略后,各个参与者的收益。
以囚徒困境为例,P={A,B},S={坦白,抵赖},U={Ua{坦白,抵赖}=Ub{抵赖,坦白}=0,Ua{抵赖,坦白}=Ub{坦白,抵赖}=-10,Ua{坦白,坦白}=Ub{坦白,坦白}=-8,Ua{抵赖,抵赖}=Ub{抵赖,抵赖}=-1}。在该博弈中,参与者都完全了解对方的行动策略以及收益函数且该博弈只进行一次,因此该博弈是完全信息静态博弈,其中(坦白,坦白)是该博弈的Nash均衡点。
重复博弈是动态博弈的一种特殊情况,是指在收益相同的情况下进行多次博弈的过程。参与人在每次博弈前,都知道历史博弈结果,且参与人的行动是同时进行的,因此参与者在选择策略时,会根据其他参与者的历史策略进行选择,同时还会考虑当前自己的行动策略对后续博弈的影响,因为自己的某一个背叛或者违约行为,都可能被其他参与人在未来进行报复。
1. 2 Nash均衡点
在博弈中,假设每个参与者都是理智且是自私的,参与者之间不存在利益承诺等其他外部因素,每个参与者在选择行动策略总是考虑是自己的收益最大。
定义2:在一个n人博弈中,如果存在行动策略s={s1,s2,…,si,…,sn},在其他参与者不改变策略的情况下,对每一个参与者i,不存在s’i策略使得参与者i的收益大于si的策略,则s称为该博弈的Nash均衡点。
Nash均衡属于非合作博弈均衡,博弈双方都不会改变自己的策略,因为单方面改变自己策略时,会导致自己的收益下降。囚徒困境中,坦白策略是每个参与者的严格优势策略,它是指无论对方采取何种策略,自己采取坦白这种策略总比其他任何策略要好,因此(坦白,坦白)成为本博弈的Nash均衡点,但是在重复博弈中,该Nash均衡点将可能被打破,最终会趋向于集体最优。
1. 3 可信度
在实际生活中,人们更希望与诚信的博弈方进行博弈,最终以实现双赢,参与者认为博弈方是否诚信,往往根据博弈方的历史策略,或者第三方的推荐建立对博弈方的信任程度,即可信度。可信度是指参与者对其他参与者的相信程度,根据其他参与者的历史选择相信为真的程度。在重复博弈中,每个参与者都相信自己的每次行动策略会影响到自己的可信度,且博弈方会根据自己的可信度在下轮博弈中采取对自己有利或者不利的行动策略。
定义3:λ是博弈中参与人A对参与人B选择某个策略的可信度,其中λ∈[-1,1]。
λ=-1,表示A对B选择某个策略完全不信任;λ=0,表示A对B选择某个策略一无所知,无法确定;λ=1,表示A对B选择某个策略完全信任。
2 算法分析
2. 1 原始博弈
在囚徒困境的单次博弈中,我们分析知道,对每个参与者来说,选择坦白的收益永远大于抵赖的收益。我们可以通过图像更直观地表示,以参与人A为例,假如B以x的概率选择坦白(h),那么B选择抵赖(d)的概率为1-x,则可以得到如下内容:
参与人A选择坦白的收益:f(h)=-8x-0*(1-x);
参与人A选择抵赖的收益:f(d)=-10x-1*(1-x)。
其中 x∈[0,1],通过图 1可知,f(d)<f(h)在 x∈[0,1]上恒成立,即无论参与人B选择何种策略,参与人A选择坦白的收益恒大于选择抵赖时的收益,与之前的分析一致。

图1参与人选择坦白与抵赖时的收益
2. 2 带可信度的重复博弈
在原始博弈中,任何一个参与者选择坦白的收益均大于选择抵赖时的收益,因此在单次博弈中,最终导致参与者们并不能达到集体最优,但是在重复博弈中,上述情况可能会得到改善。
依然以囚徒困境为例进行重复博弈,在每轮博弈前,参与人都了解其他博弈方的历史决策,并依据博弈方的历史决策建立可信度。λ是参与人A对参与人B选择坦白策略时的可信度,λ=-1表示参与人A完全不相信B会选择坦白;λ=0表示参与人A对B选择何种策略一无所知;λ=1表示参与人A完全相信B会选择坦白。且当A以λ的可信度相信B会选择坦白时,则同时以-λ的可信度相信B会选择抵赖,则可以得到以下内容:
参与人A选择坦白的收益:
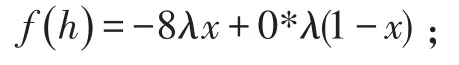
参与人A选择抵赖的收益:

如果希望参与人A在重复博弈中选择抵赖时的收益大于坦白时的收益,则需要满足 f(d)>f(h),即:


图2参与人A的收益
通过分析可知,在重复博弈中,参与人在选择策略时,不仅仅会考虑在每轮博弈中自己的收益,会更多考虑博弈方的可信度,依据历史情况动态修改可信度,以便在下轮博弈中选择更合适的策略,使自己收益最大,同时也会考虑自己的选择对后续博弈的影响,因此可信度的出现,将会约束参与人更加理性地选择自己的策略。
3 结语
在单次囚徒困境博弈中,(坦白,坦白)策略是该博弈的Nash均衡点,在没有其他参与人改变策略的情况下,该策略使得参与人的收益最大,每个参与者都仅仅只考虑当前策略对自己收益的影响,尽可能使自己的收益最大化。在基于可信度方法的重复博弈中,参与人不仅仅只关系当前策略对自己收益的影响,会更多考虑博弈方在后续博弈中采取的策略,而博弈方采取有利或者不利于自己的策略又与自己的历史策略有关。
本文集中讨论了在重复博弈中,利用可信度方法将打破单次博弈中的Nash均衡点,最终使整个系统趋向整体最优,但本文没有考虑根据其他参与人的历史策略如何修正可信度,以体现博弈方的策略在未来的博弈中给予奖励或者惩罚措施,下一步工作将讨论如何修正可信度的方法。

