PROPERTIES OF SOLUTIONS OF n-DIMENSIONAL INCOMPRESSIBLE NAVIER-STOKES EQUATIONS∗
Linghai Zhang
(Dept.of Math.,Lehigh University,17 East Memorial Drive,Bethlehem,Pennsylvania 18015,USA)
Abstract Consider the n-dimensional incompressible Navier-Stokes equations
Keywords the n-dimensional incompressible Navier-Stokes equations;decay estimates with sharp rates;exact limits;appropriate coupling of existing ideas and results;Fourier transformation;Parseval’s identity;Lebesgue’s dominated convergence theorem;Gagliardo-Nirenberg’s interpolation inequality
1 Introduction
1.1 Mathematical model equations
Consider the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations
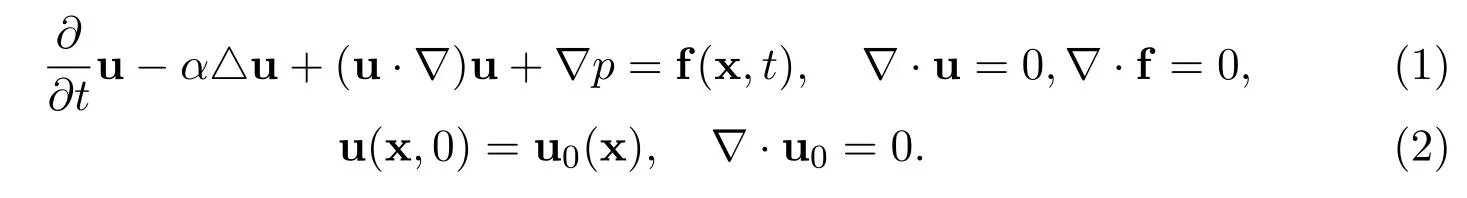
The real vector valued function u=u(x,t)represents the velocity of the fluid at position x and time t.The real scalar function p=p(x,t)represents the pressure of the fluid at x and t.The positive constant α>0 represents the diffusion coefficient.See Leray[7],Temam[14]and[15].
Consider the Cauchy problem for the linear heat equation

Can we use the solution of the linear heat equation to approximate the solution of the Navier-Stokes equation?Theorems 2 and 4 given in Subsection 1.5 not only provide a positive solution but also demonstrate how well it approximates.
1.2 Previous related results
Let us review several well known results about the n-dimensional incompressible Navier-Stokes equations(1)-(2).
The existence and regularity of the global weak solutions:First of all,let us consider the case n=2.If the initial functionand the external forcethen there exists a unique global smooth solution
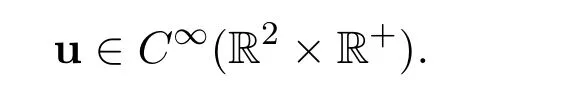
See Leray[7],Temam[14]and[15].Secondly,let us consider the case n ≥3(basically,n=3 or n=4).Suppose that the initial functionand the external forceThen there exists a global weak solutionsuch thatMoreover,there holds the following elementary uniform energy estimate
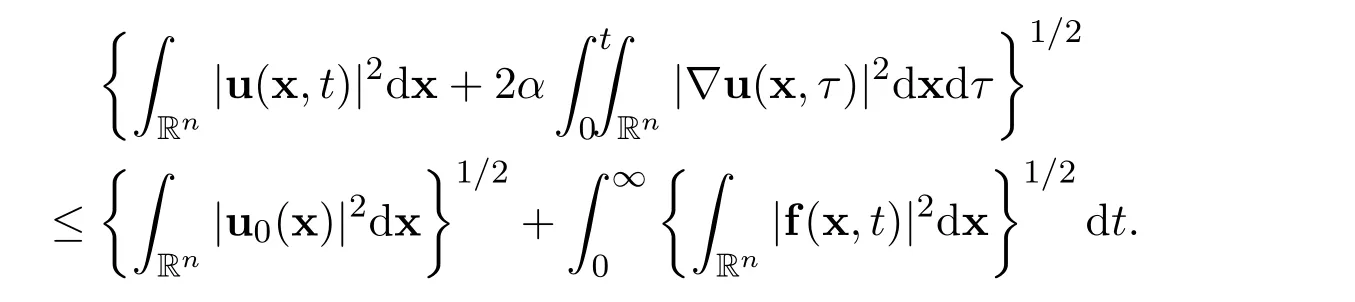
Additionally,there holds the following formal representation for the global weak solution
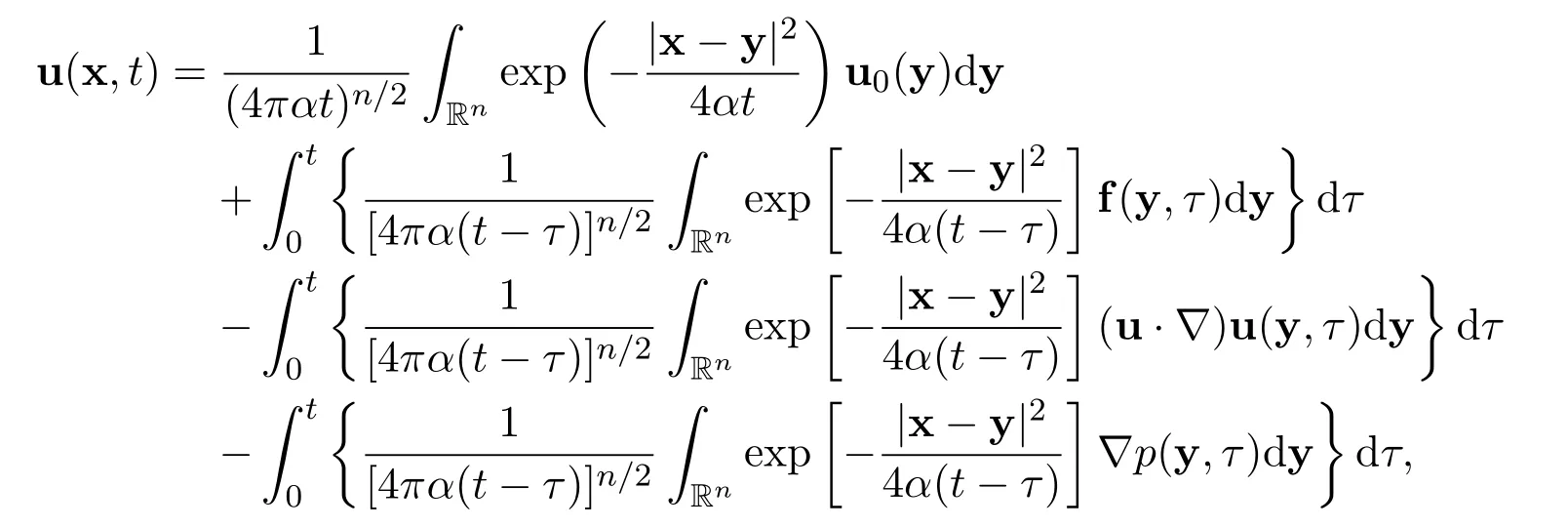
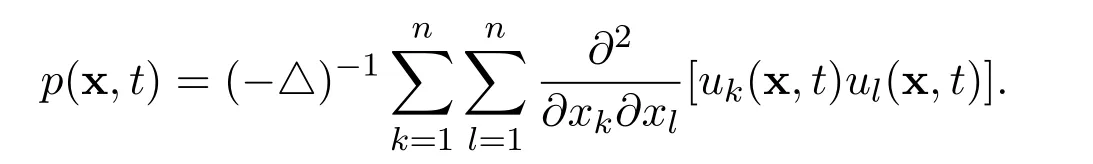

A very interesting,natural question arises: When the global weak solutions become a global smooth solution?Under appropriate conditions,there are positive solutions to this important question.First of all,if the initial functionand the external forceare reasonably small,then there exists a unique global smooth solutionSee Fujita and Kato[2]and Lei and Lin[5].Ifandand if there exist positive constants λ>n ≥3 andµ>2,with n/λ+2/µ≤1,such that
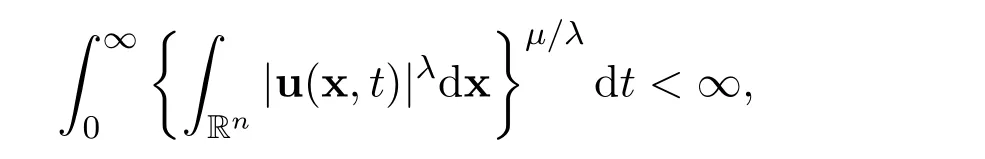
then the global weak solutions become the global smooth solution
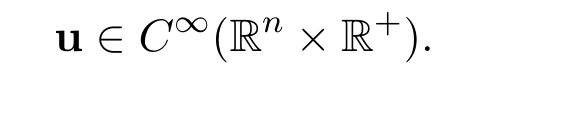
See Serrin[10].
Very recently,Lei and Lin[5],Lei,Lin and Zhou[6],Peng and Zhou[12]established very interesting results for(1)-(2),including the existence of large global smooth solution with special initial function for n=3.In particular,Lei,Lin and Zhou derived new uniform energy estimate by virtue of a special structure of helicity,which is crucial with respect to the natural scalings for(1). The new energy functional is coercive for a class of initial functions.Then they constructed a family of large global smooth solutions of(1)-(2)with finite energy based on the uniform energy estimate in[6].
Decay estimates with sharp rates:Suppose that the initial function u0∈and the external forceThen

for all time t>0.Moreover,there hold the following the decay estimates with sharp rates
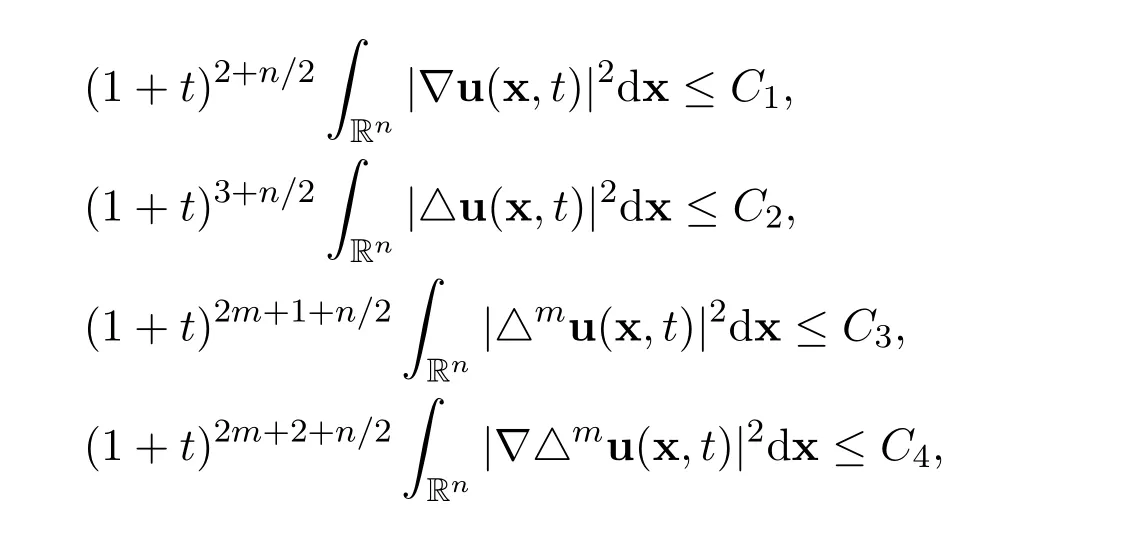
for all positive integers m ≥1 and for all time t ≥T,where C0>0,C1>0,C2>0,C3>0 and C4>0 are positive constants,independent of u and(x,t).See Oliver and Titi[9]and Schonbek and Wiegner[13].
1.3 Main motivations,main purposes,main difficulties and main strategies
Motivation:Consider the Cauchy problem for the homogeneous heat equation
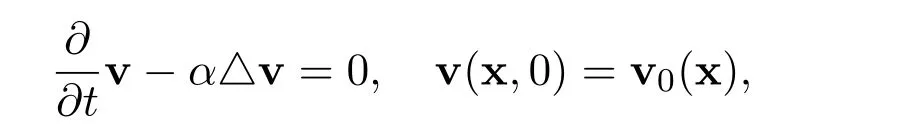
where α>0 is a positive constant. Let the initial functionThere exists a global smooth solution,given explicitly by
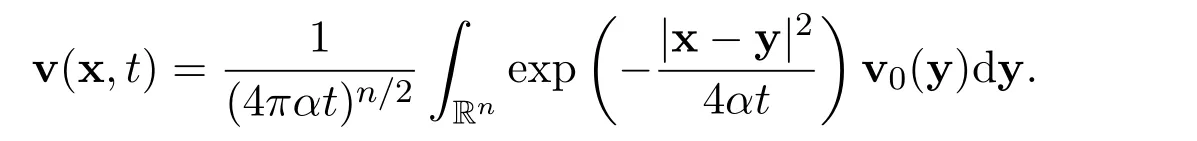
It is very easy to derive the representation of the Fourier transformation
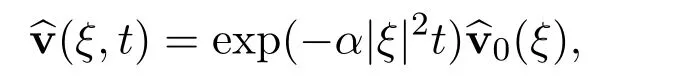
Let m ≥0 be any integer.Then by using Parseval’s identity,the representation of the Fourier transformation,Lebesgue’s dominated convergence theorem and a simple change of variables,we have the following exact limit
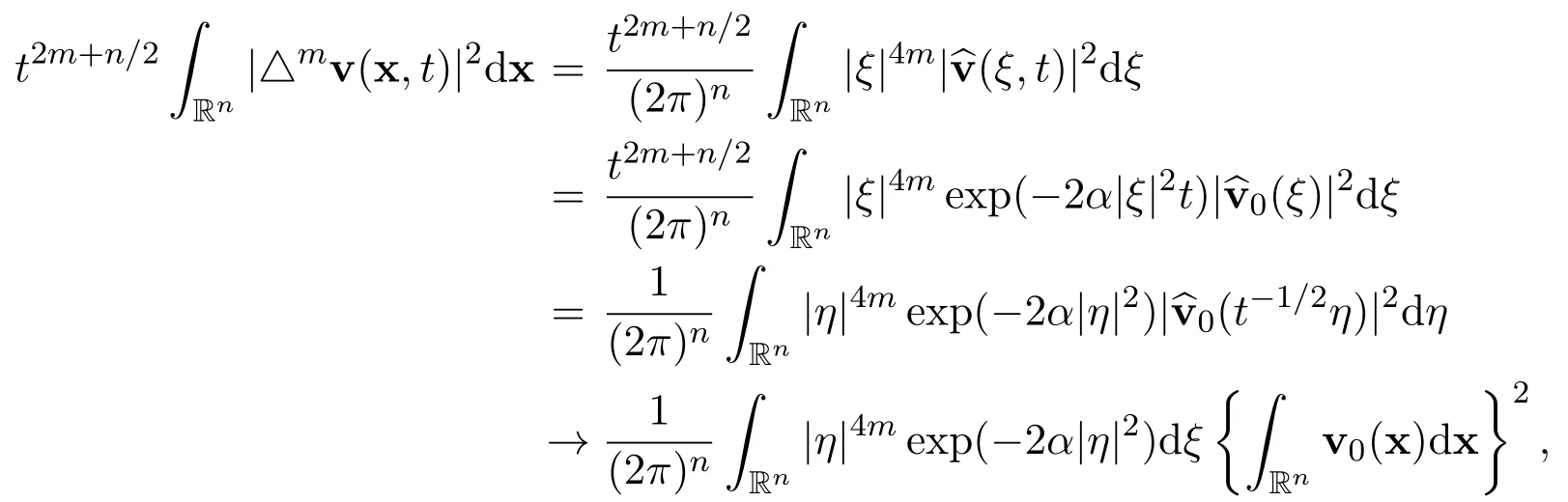
as t →∞.
Very similarly,we have

as t →∞.These limits are optimal if

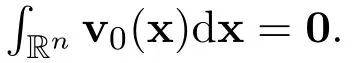
Motivated by the exact limits of the global smooth solution of the homogeneous heat equation,we will establish the exact limits of the global weak solutions of the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations.Let u=u(x,t)represent the global weak solutions of(1)-(2)corresponding to u0=u0(x)and f=f(x,t),and let v=v(x,t)represent the global smooth solution of(3)-(4)corresponding to v0=u0(x)and r=f(x,t). The first purpose is to establish the following estimates

and
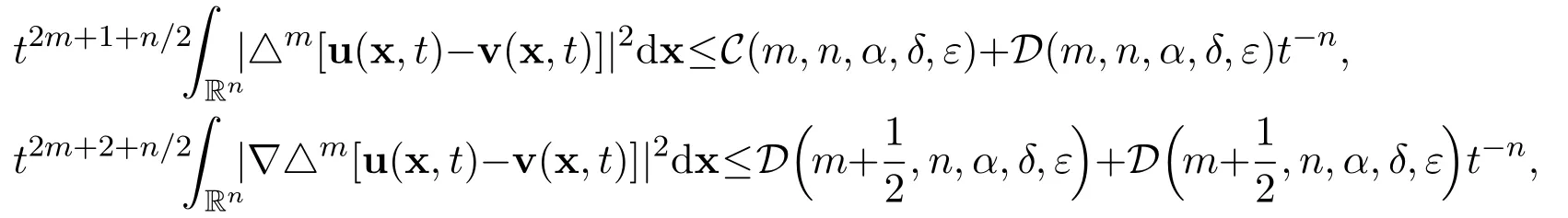
for all positive integers m ≥1 and for all time t ≥T,where A(m,n,α,δ,ε),B(m,n,α,δ,ε),C(m,n,α,δ,ε),D(m,n,α,δ,ε)are positive constants,independent of time t,0<δ<1 and 0<ε<1 are small positive constants.
The main purpose of this paper is to accomplish the following exact limits
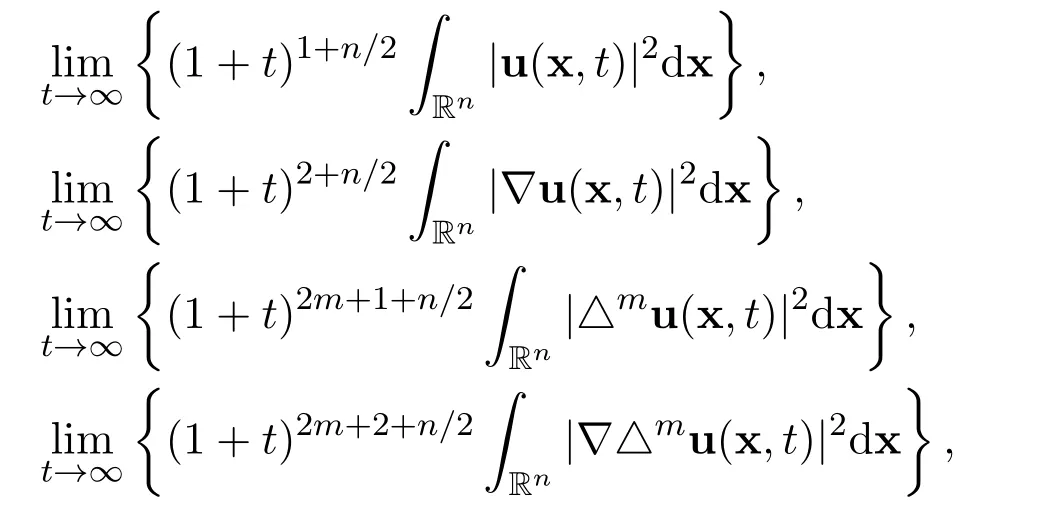
and
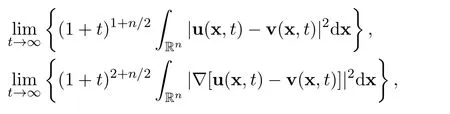
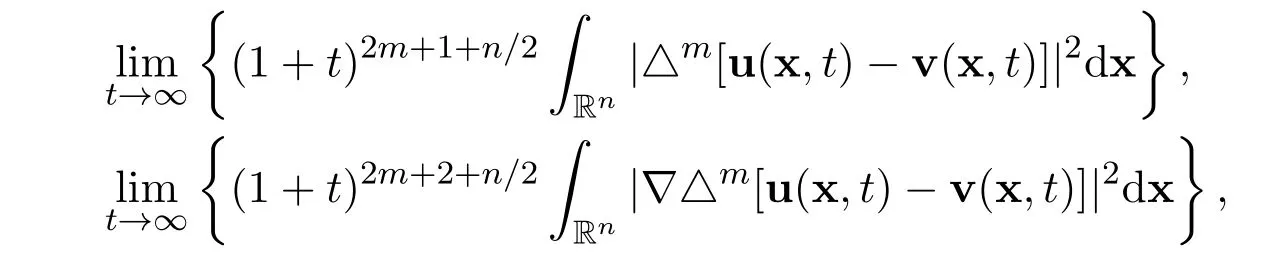
for all positive integers m ≥1,in terms of the following integrals
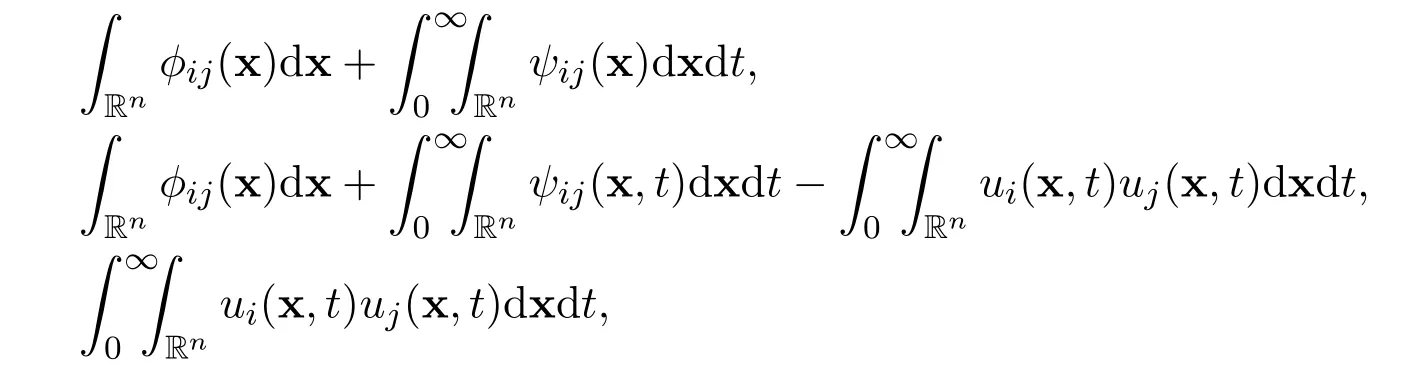
where ϕij=ϕij(x)are functions related to the initial function and ψij=ψij(x,t)are functions related to the external force,for all i=1,2,3,···,n and j=1,2,3,···,n.
Here are more motivations to study the exact limits:
(1)to study the influence of the nonlinear functions(u·∇)u and ∇p on the limits;
(2)to study the influence of the initial function u0and the external force f on the limits;
(3)to study the influence of a special structure of the n-dimensional incompressible Navier-Stokes equations on the limits;

One technical difficulty to study the exact limits is that the integral
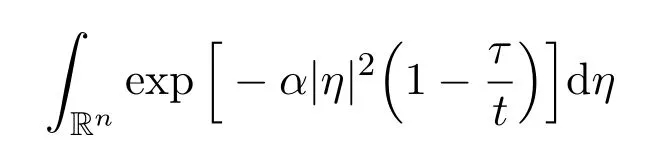
of the exponential functionwith respect to η overis divergent at τ=t,for all t>0. One of the main technical advances is to make use of the decay estimates with sharp rates for the derivatives of the global weak solutions and the following particular integral
to control the integral
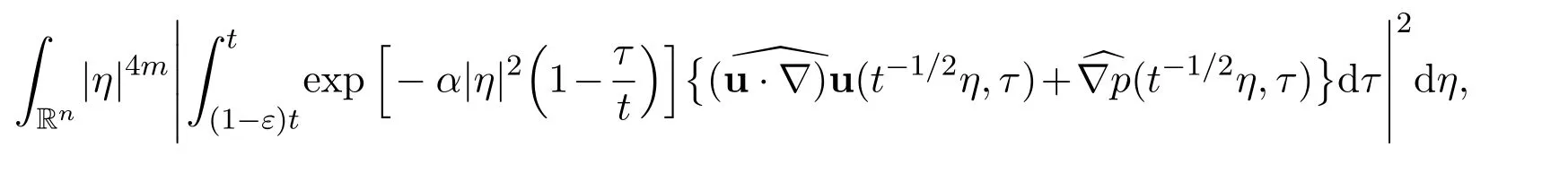
for all positive integers m ≥1 and for all sufficiently large time t ≥T,where 0<δ<1 and 0<ε<1 are small positive constants.
The uniform energy estimates of all order derivatives of the global weak solutions for the general case(when both the initial function and the external force are large)have been open. Therefore,the existence and uniqueness of the global smooth solutionof(1)-(2)have been open.For the main purposes,we only need the existence and decay estimates with sharp rates of the local smooth solution on(T,∞).These results are well known.
Here are the main strategies to establish the exact limits of

First of all,we will couple together the Fourier transformation,Parseval’s identity,appropriate decomposition of the temporal interval[0,t],Lebesgue’s dominated convergence theorem and Gagliardo-Nirenberg’s interpolation inequality in a new way to establish the exact limits for the global smooth solution of the Cauchy problem for the heat equation.Then we will couple together the special structure of the ndimensional incompressible Navier-Stokes equations,some uniform energy estimates,the decay estimates with sharp rates of the derivatives of the global weak solutions for all sufficiently large time and the exact limits for the linear heat equation to accomplish the exact limits of the global weak or smooth solution of the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations(1)-(2).
1.4 Mathematical assumptions
Let us make the following assumptions for the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations.
(A1)Suppose that the initial functionand the external forcefor all positive integers m ≥1.
(A2)Suppose that there exist real scalar functionsandfor all i=1,2,3,···,n and j=1,2,3,···,n,such that
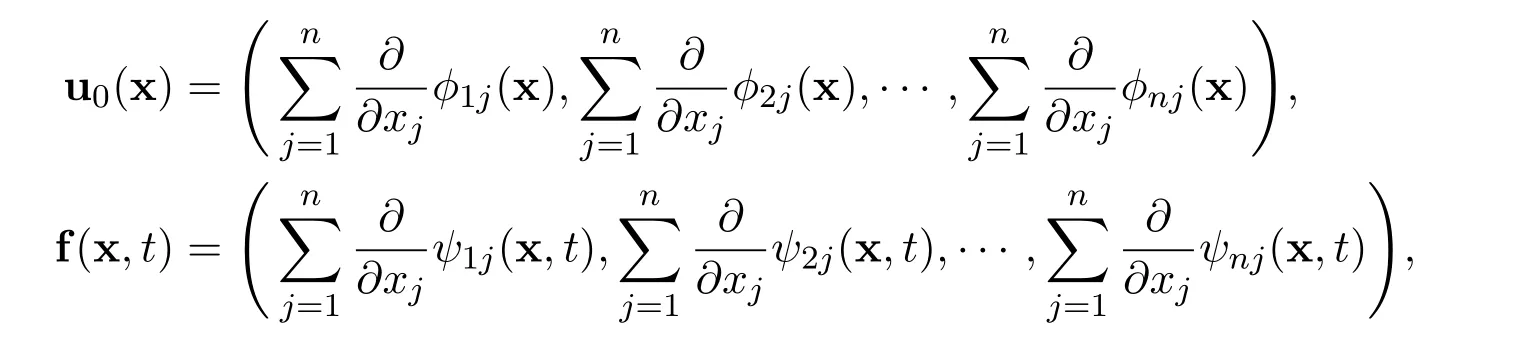
Remark 1The assumptions in(A2)are motivated by the incompressible conditions ∇·u0=0 and ∇·f=0,by the integrals
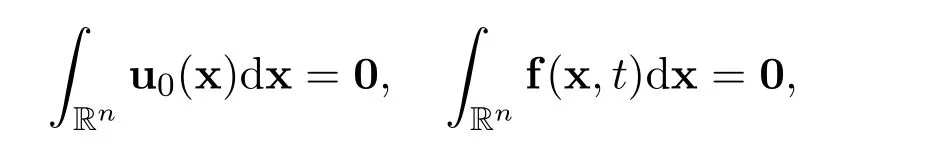
for all t>0,and by the special structure of the nonlinear functions(u·∇)u and∇p.
(A3)Suppose that there exist the following integrals
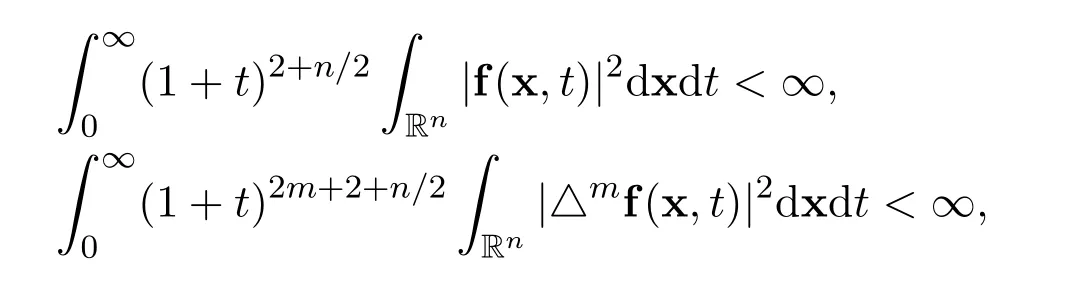
for all positive integers m ≥1.
(A4)Let 0<δ<1 and 0<ε<1 be small positive constants. Suppose that there exist the following limits
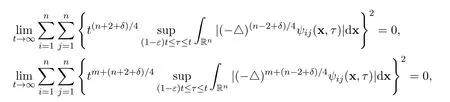
for all positive integers m ≥1.
Motivation for(A5).Let the initial functionand the external forceThen there exists a global weak solutionsuch thatIt is well known that after a long time,the global weak solutions become sufficiently small and sufficiently smooth and there hold the decay estimates with sharp rates for the global weak solution,for all sufficiently large t ≥T,see Leray[7]. Without loss of generality,for the purposes of establishing the exact limits,we may assume that there exists a global smooth solution,that is,such thatfor all positive integers m ≥1.However,we will not use the existence or the uniqueness of the global smooth solution in the mathematical analysis.
(A5)Suppose that there exists a unique global smooth solution to the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations:such thatfor all positive integers m ≥1.Moreover,suppose that there hold the following decay estimates with sharp rates

for all positive integers m ≥1 and for all time t>0,where C0>0,C1>0,C2>0,C3>0 and C4>0 are positive constants,independent of u and(x,t),they depend on the following integrals of the initial function and the external force:
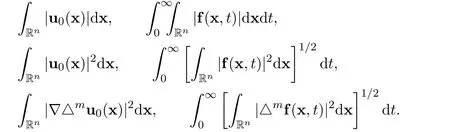
We do not assume that the initial function u0and the external force f are small.
1.5 Main results
Definition 1Let ρ>0 be a positive constant. Define the fractional order derivative(−△)ρϕ by using the Fourier transformation
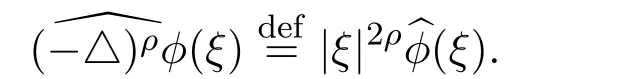
Let u=u(x,t)represent the global smooth solution of the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations corresponding to the initial function u0=u0(x)and the external force f =f(x,t). Let v=v(x,t)represent the global smooth solution of(3)-(4)corresponding to the initial function v0=u0(x)and the external force r=f(x,t). Let the assumptions(A1),(A2),(A3),(A4)and(A5)hold.Let 0<δ<1 and 0<ε<1 be small positive constants.
Theorem 1There hold the following estimates for the global smooth solution of(1)-(2)
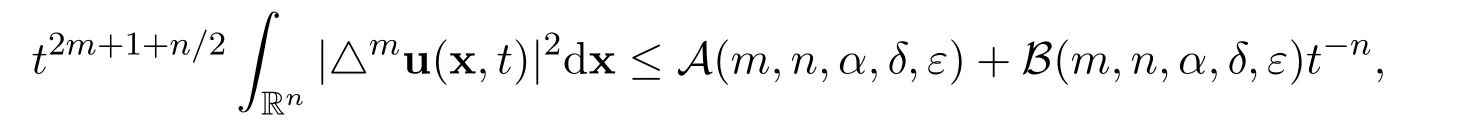
and
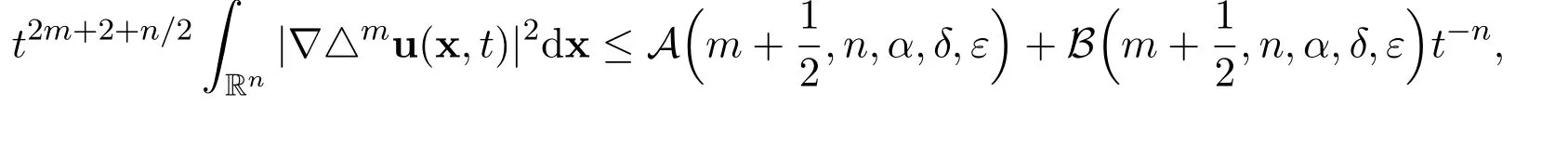
for all positive integers m ≥1 and for all time t>0,where

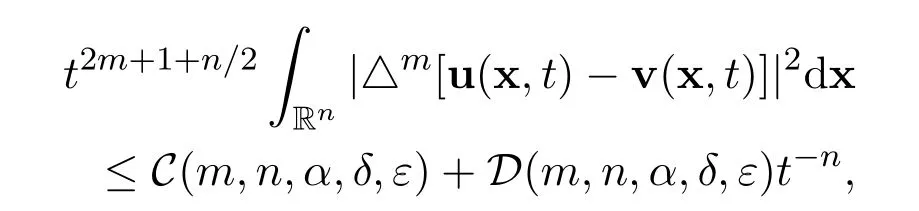
and
Theorem 2There hold the following estimates

for all positive integers m ≥1 and for all time t>0,where
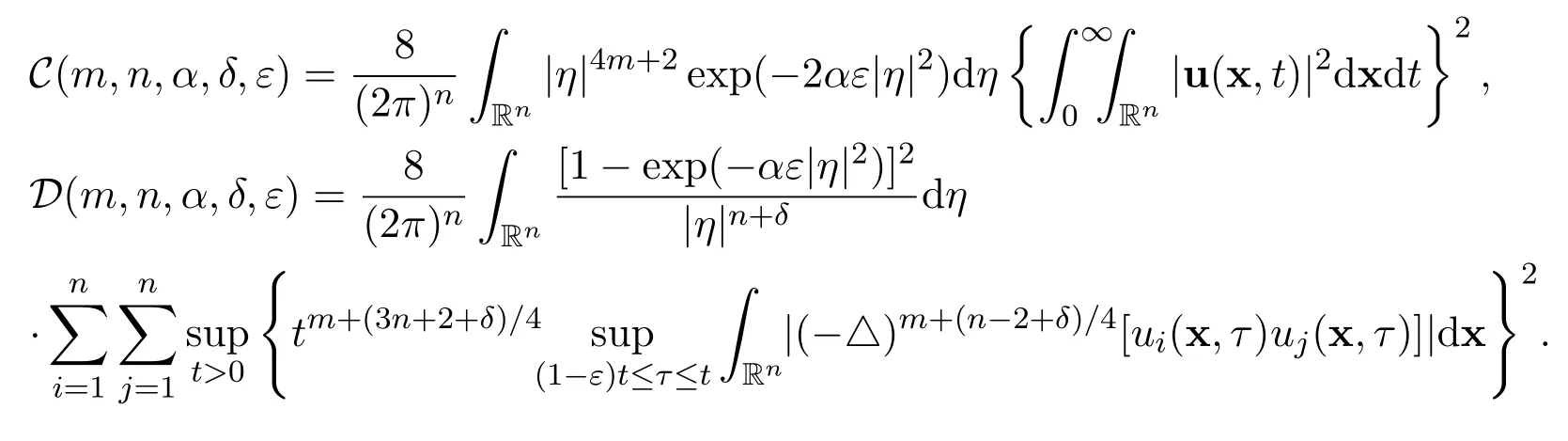
Remark 2The estimates in both theorems are true for all t>0 if there exists a global smooth solution,and the estimates are true for all t ≥T ≫1 if there exists a global weak solution.The limits of the last terms in all of the above estimates are equal to zero,as t →∞.Note that there hold the following estimates for the global smooth solution

for all positive integers m ≥1 and for all time t>0,where C1>0,C2>0 and C3>0 are positive constants,independent of u and(x,t).
Definition 2Let the assumptions(A1),(A2),(A3),(A4)and(A5)hold.Let
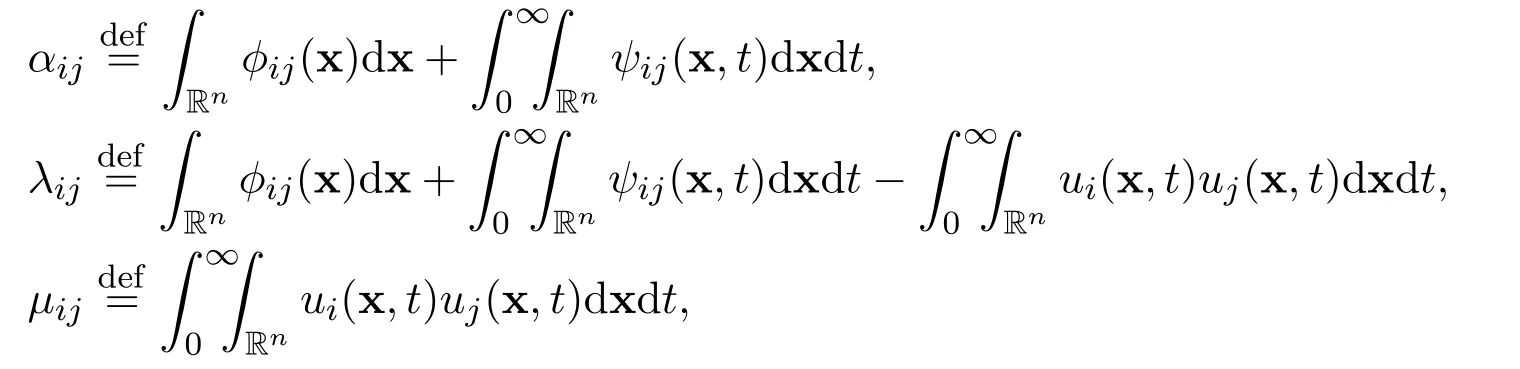
for all positive integers i=1,2,3,···,n and j=1,2,3,···,n.
Theorem 3There hold the following exact limits
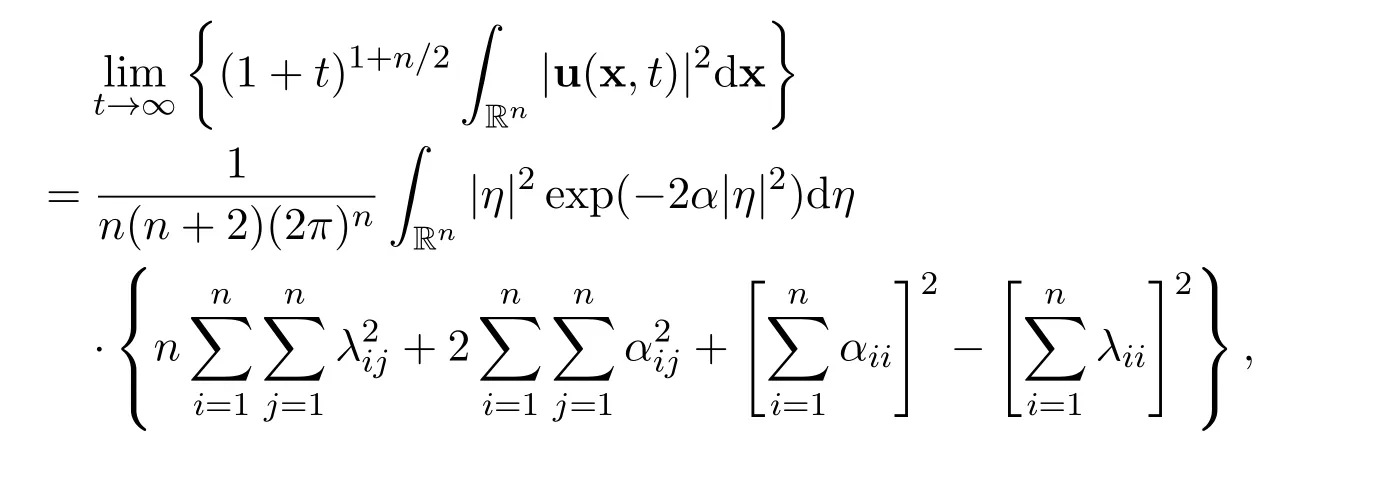
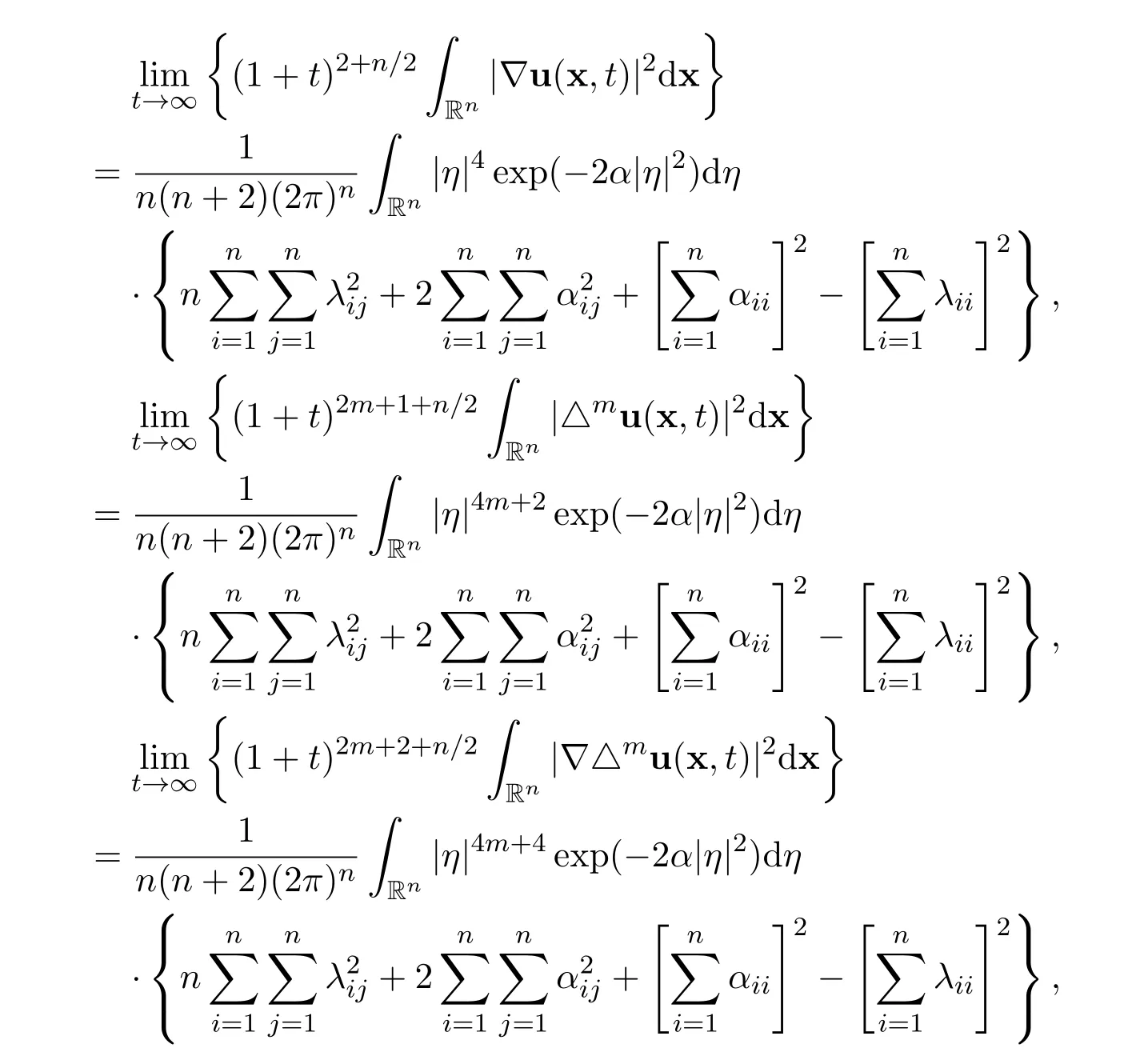
for all positive integers m ≥1.
Theorem 4There hold the following exact limits

for all positive integers m ≥1.
Note that we may make these results more explicit by using the precise values
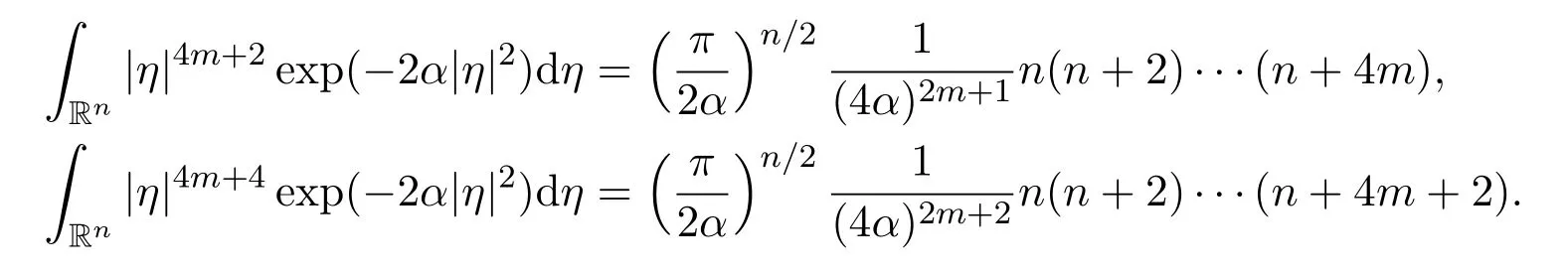
2 Mathematical Analysis and Proofs of the Main Results
2.1 Linear analysis
The main purpose of this subsection is to establish the exact limits of the global smooth solution of the heat equation.Let the initial functionand the external forceThen there exists a unique global strong solutiongiven explicitly by

Theorem 5Let the initial functionand the external force r ∈Suppose that
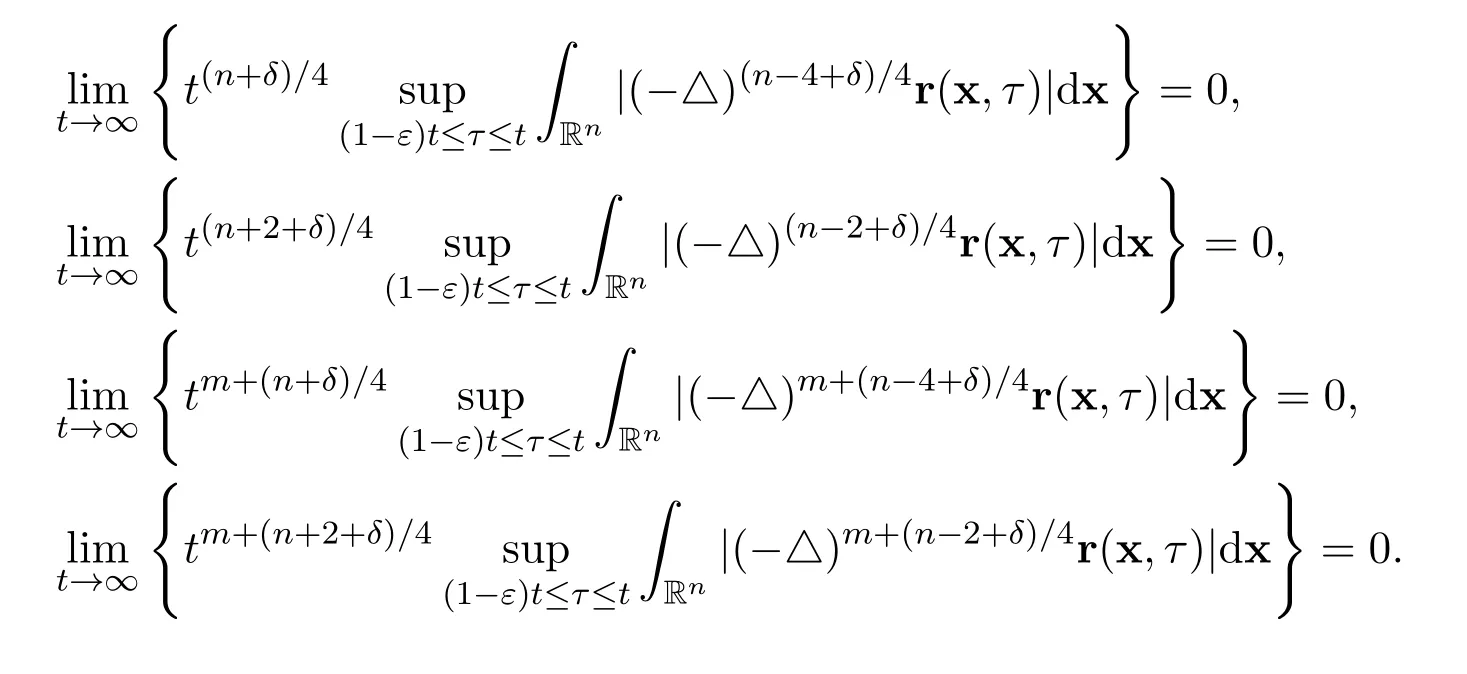
Then there hold the following exact limits for the global smooth solution of the Cauchy problem for the heat equation
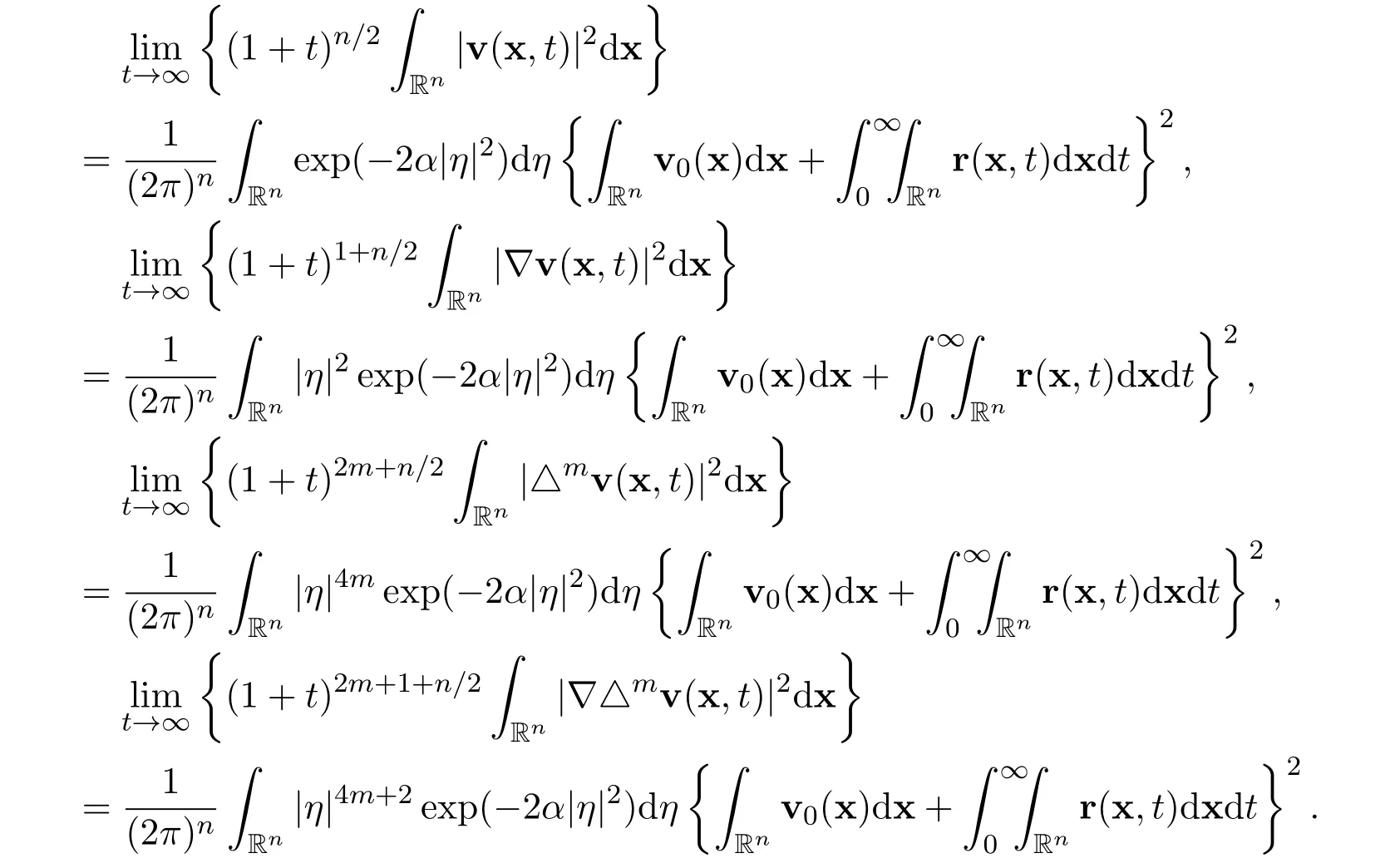
Theorem 6Let the initial functionand the external force r ∈Suppose that there exist real scalar functions ϕij∈andfor all i=1,2,3,···,n and j=1,2,3,···,n,such that

Let 0<δ<1 and 0<ε<1 be small positive constants,such that
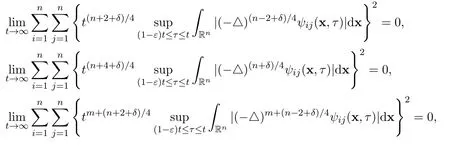
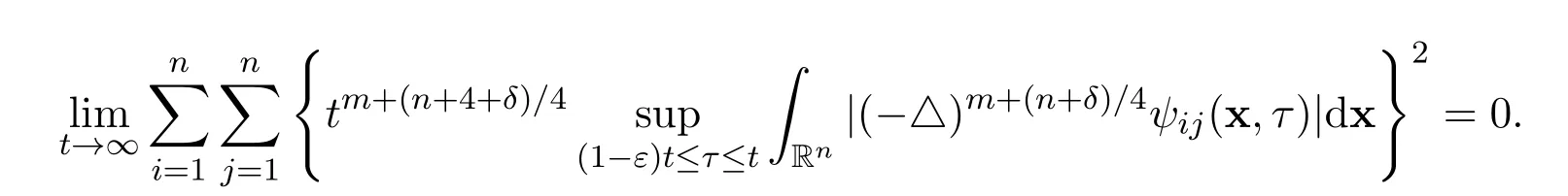
Then there hold the following exact limits for the solution of the Cauchy problem for the heat equation
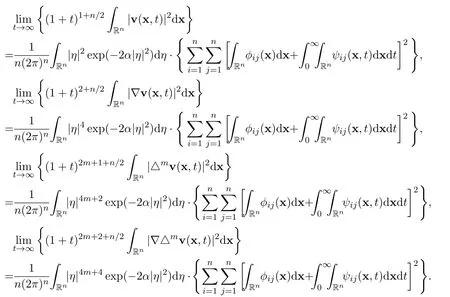
The proofs of Theorems 5 and 6 consist of the following four lemmas.
Remark 3LetandFor the heat equation,there hold the following representations

where η=t1/2ξ and t>0.Let us consider the exponential function exp[−α|η|2(1 −of τ on the closed interval[0,t].Obviously,there exists a positive lower bound foron the interval[0,(1 −ε)t]. However,there is no positive lower bound foron[(1 −ε)t,t]. This means that we will treat the exponential functionvery differently on the intervals[0,(1 −ε)t]and[(1 −ε)t,t].
Lemma 1LetandThen there hold the following exact limits
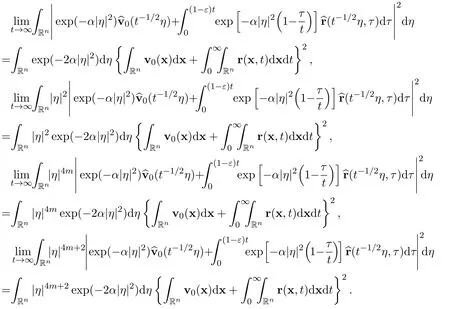
ProofWe will apply Lebesgue’s dominated convergence theorem to establish these limits.Clearly,there holds the following estimate
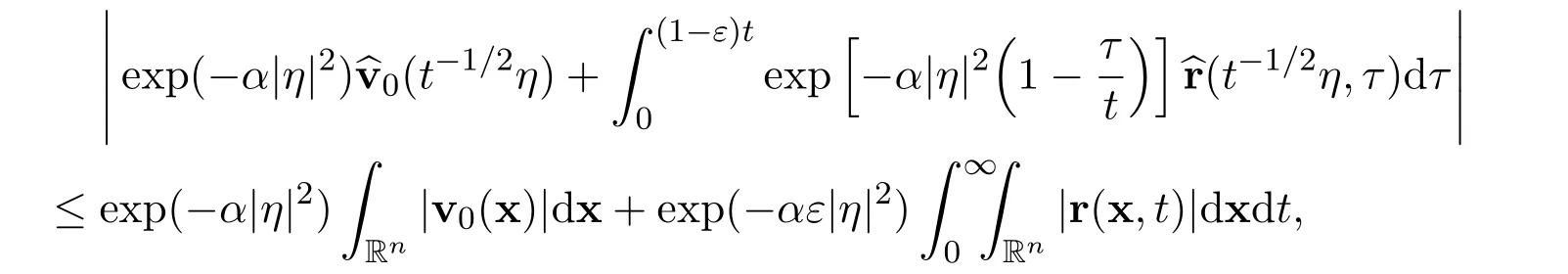
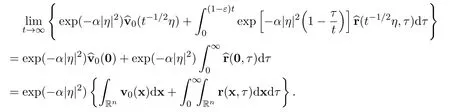
The proof of Lemma 1 is finished.
Lemma 2LetThen there hold the following limits

ProofThe proof consists of several steps.First of all,for alland t>0,we have
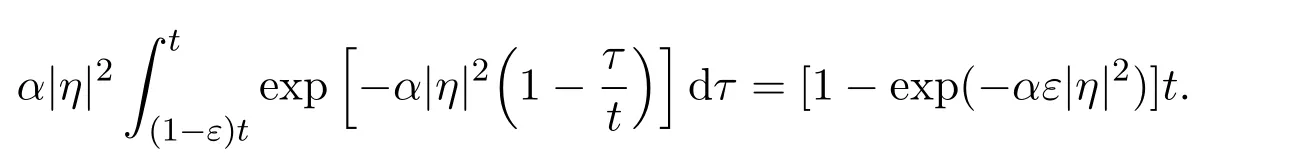
There exists the following integral
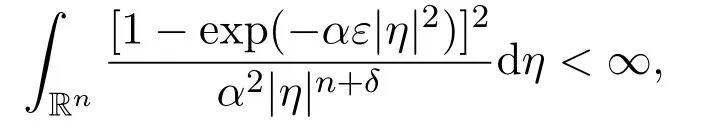
due to the existence of the following limit
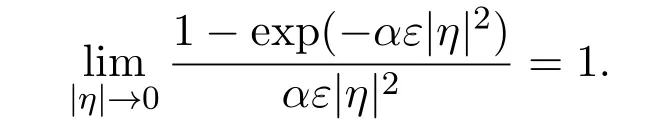
Note that

Let η=t1/2ξ.Then there hold the following estimates
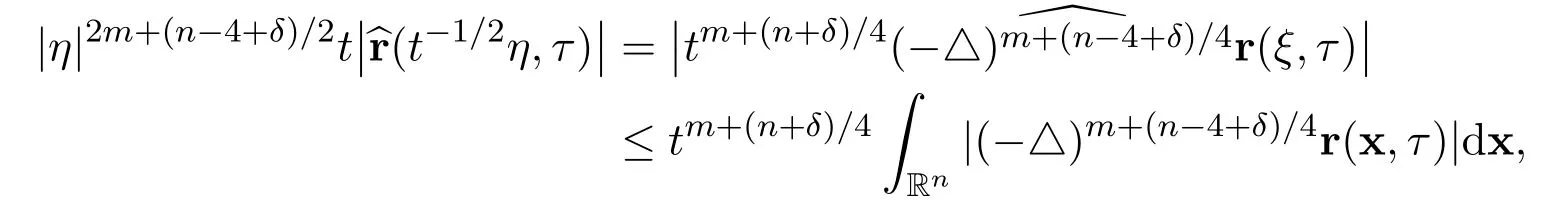
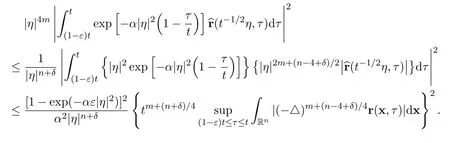
Therefore,there holds the following estimate
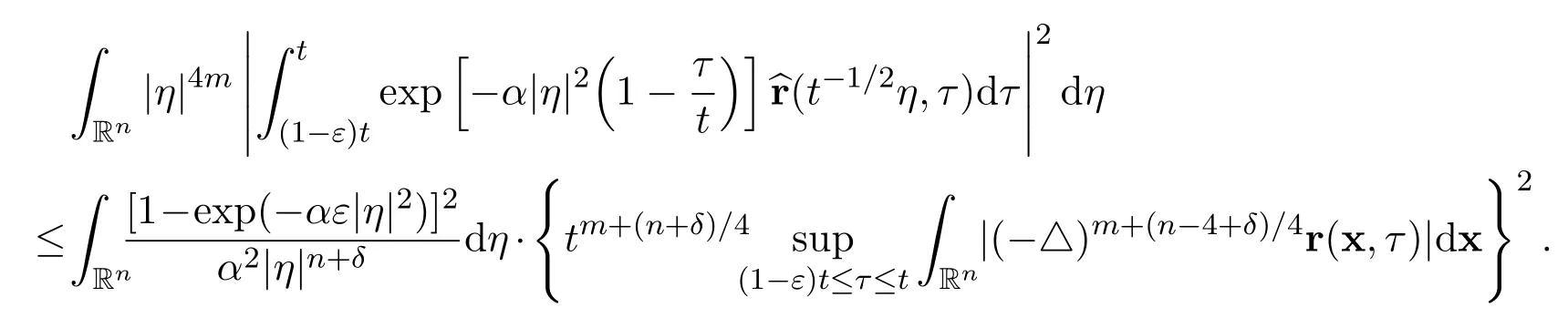
Now we have
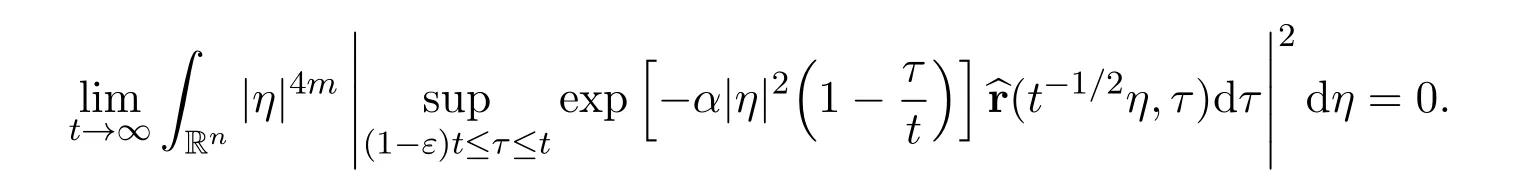
Very similarly
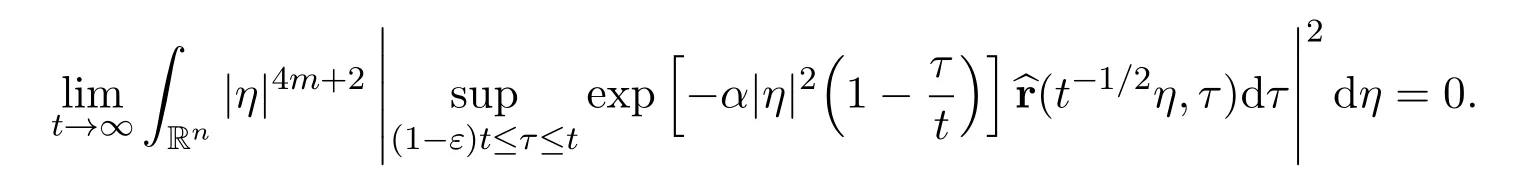
The proof of Lemma 2 is finished.
Lemma 3LetandThen there hold the following limits

ProofWe will couple together the exact limits in Lemmas 1 and 2 to finish the proof of Lemma 3.Define the following complex,vector valued,auxiliary functions
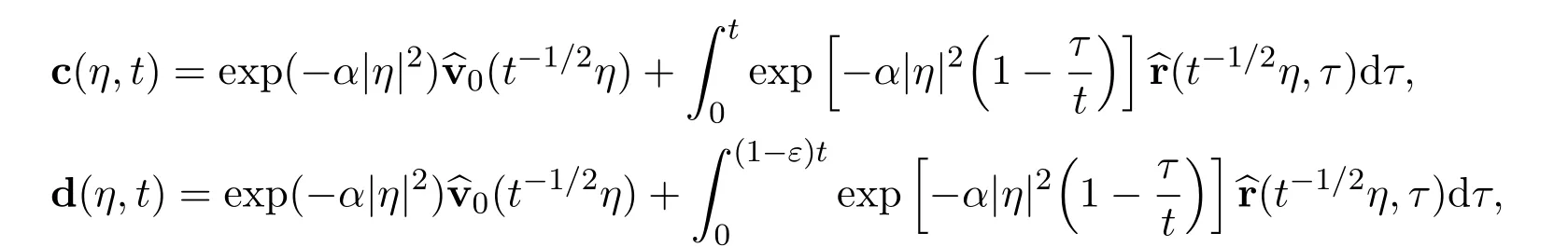
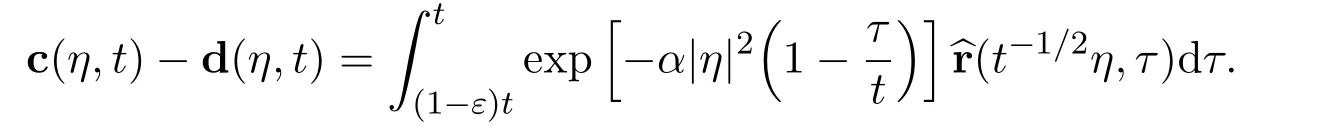
Therefore,there hold the following estimates and limit
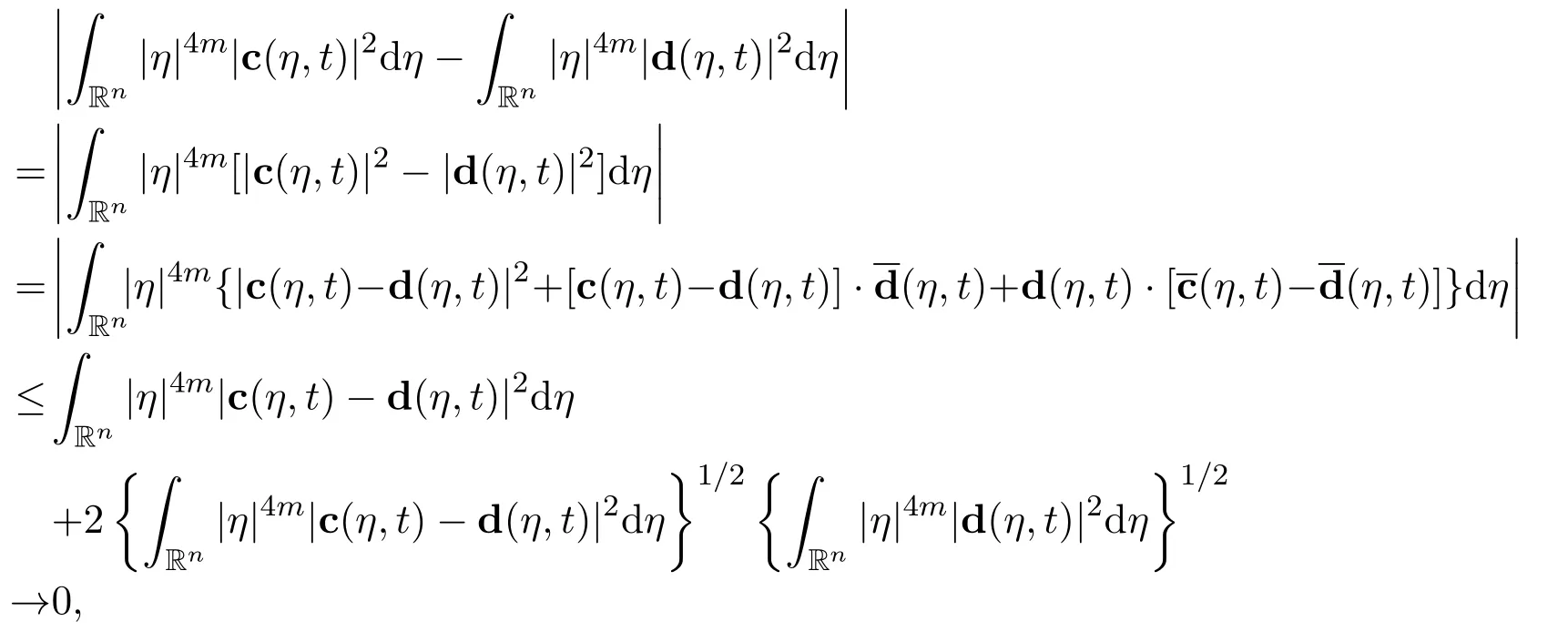
as t →∞,by using the results of Lemmas 1 and 2.Therefore

Very similarly,
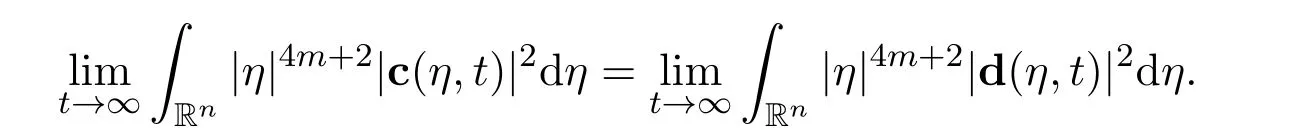
The proof of Lemma 3 is finished.
Lemma 4LetandThen there hold the following exact limits
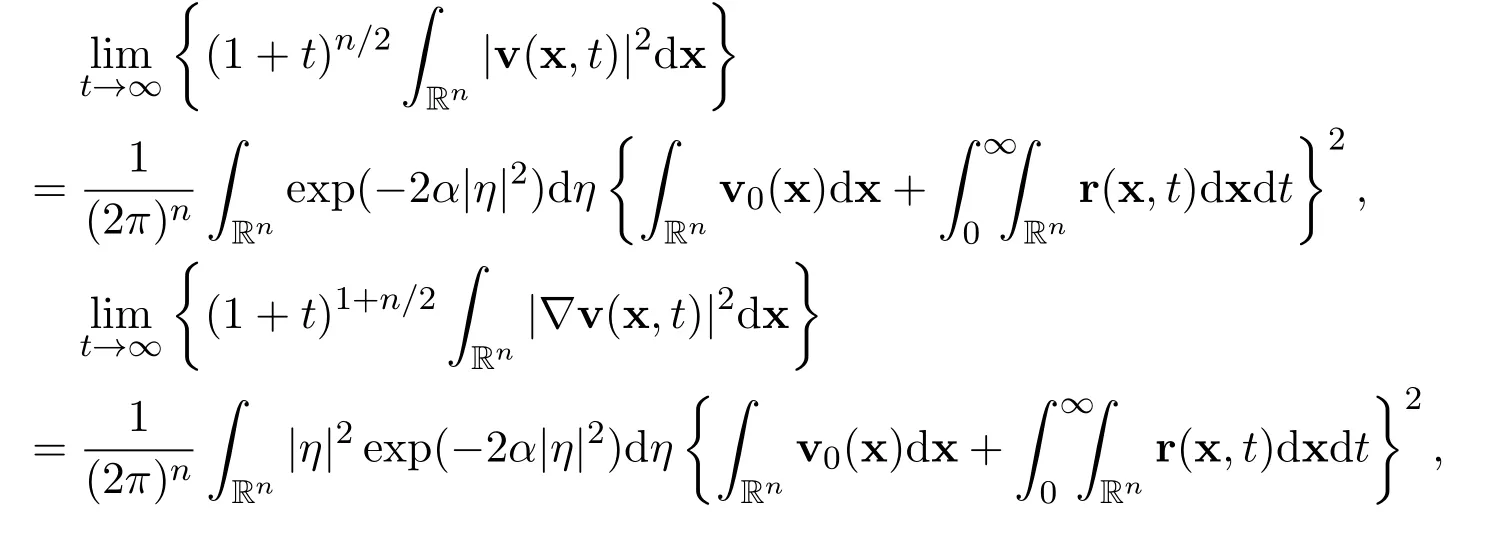
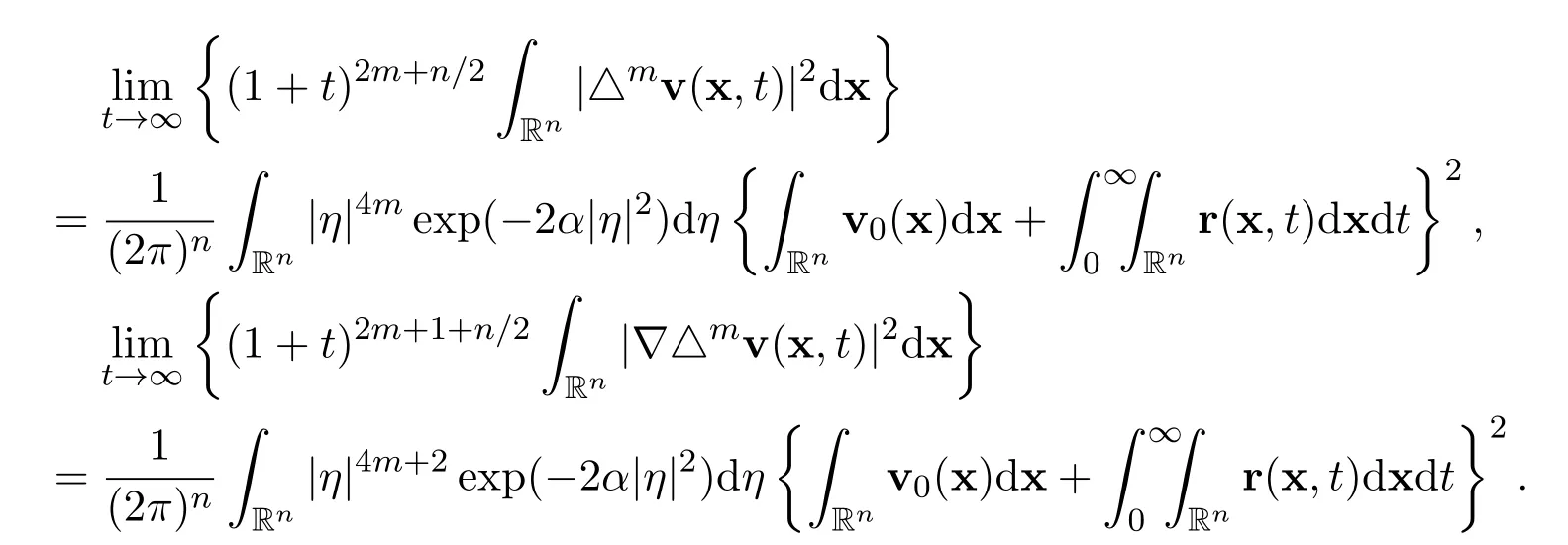
ProofThe Fourier transformation of the global smooth solution of the linear heat equation vt−α△v=r(x,t)may be represented as

as t →∞,by using the results of Lemmas 1-3.Very similarly,we have
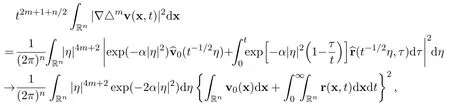
as t →∞.The proof of Lemma 4 is finished.
Proof of Theorem 5The proof is finished by coupling together the four lemmas.
Proof of Theorem 6It is very similar to the proof of Theorem 5 and it is omitted.
Remark 4For the following slightly more general function
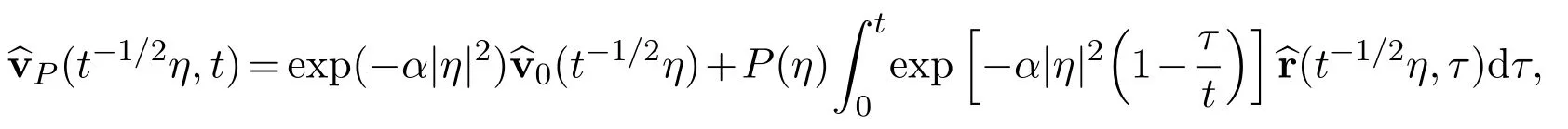
where P is a homogeneous function,that is,P(rη)=P(η),for allandwe may establish very similar exact limits.
2.2 Nonlinear analysis
The main purpose of this subsection is to make use of the special structure of the n-dimensional incompressible Navier-Stokes equations and the linear results to accomplish the exact limits of the global smooth solution of the Cauchy problem.There exists a special structure in the Navier-Stokes equations.Note that
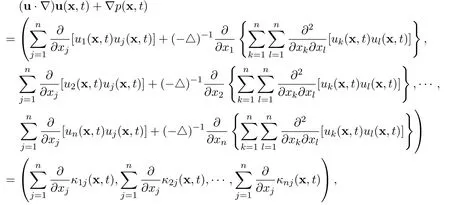
where
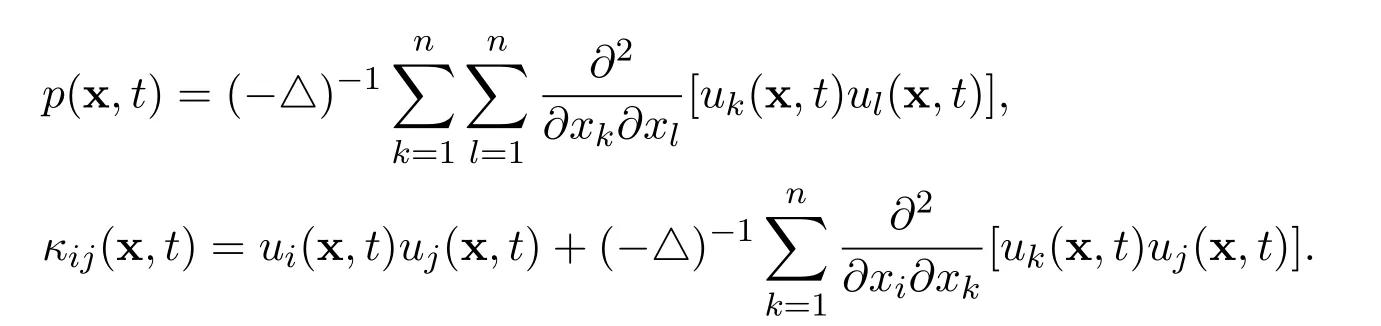
Below,we regard
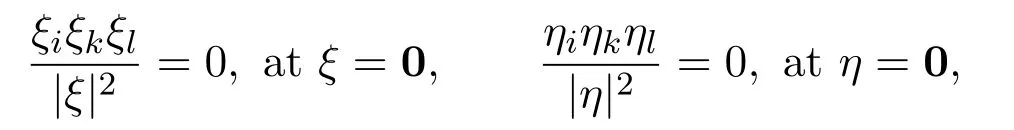
for all i=1,2,3,···,n,k=1,2,3,···,n and l=1,2,3,···,n.
Proof of Theorem 1Taking the divergence of the Navier-Stokes equations yields
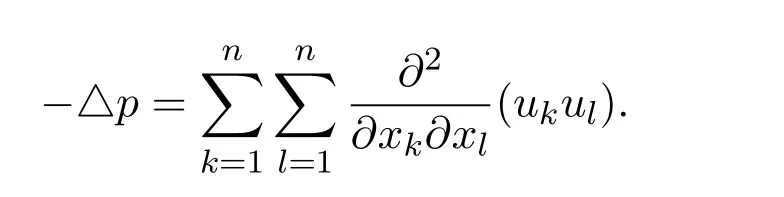
Performing the Fourier transformation to this equation and applying some simple properties lead to
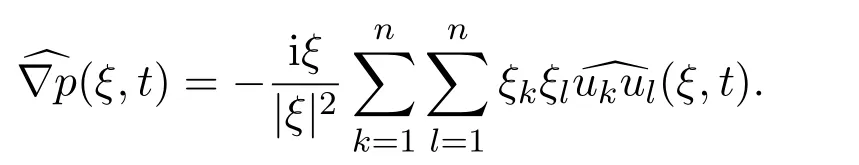
First of all,let us rigorously derive the representation of the Fourier transformationPerforming the Fourier transformation to the incompressible Navier-Stokes equations and multiplying the result by the integrating factor exp(α|ξ|2t),integrating the result with respect to time t and then rearranging terms lead to the representation
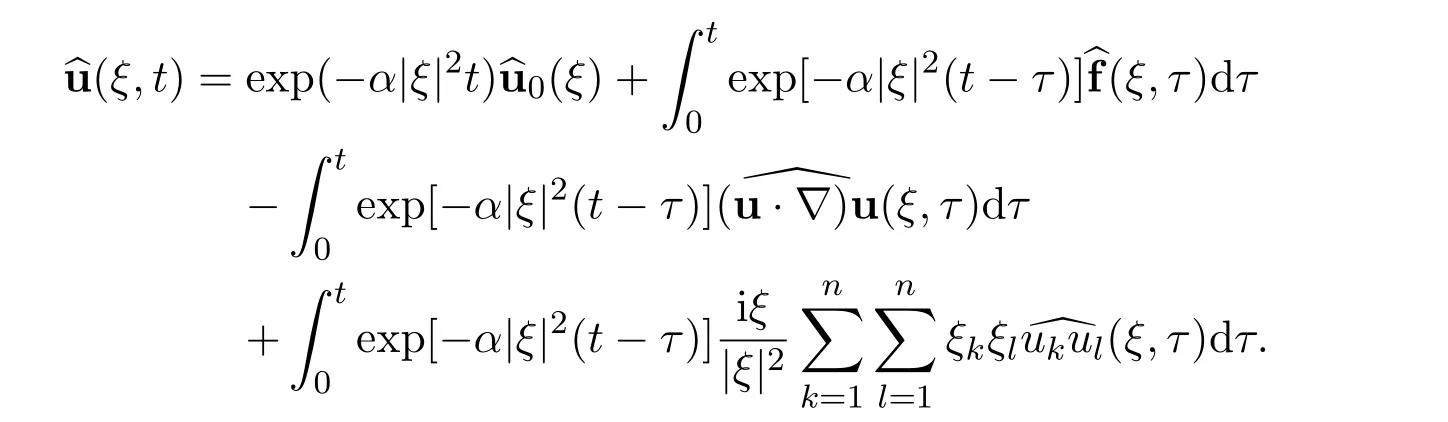
Let us make the change of variables η=t1/2ξ,where t>0.Then

Recall that the initial function and the external force are given by

Performing the Fourier transformation to these functions leads to
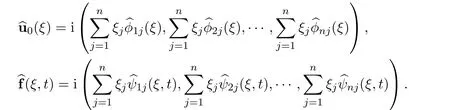
Let us multiply the i-th component ofby t1/2.We have
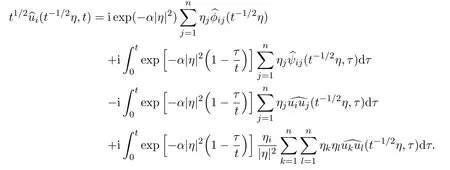
By using Parseval’s identity and the above representation of the Fourier transformation,we have the following elementary estimates

for all t>0.Let us make use of the Cauchy-Schwartz’s inequality to make estimates for these integrals one by one.
First of all,we have

Therefore,there holds the following estimate for the first integral
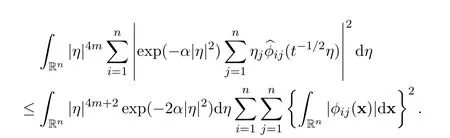
Secondly,it is easy to show that
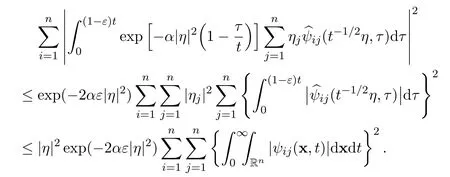
Therefore,there holds the following estimate for the second integral
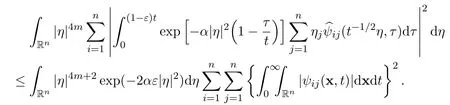
Thirdly,note that
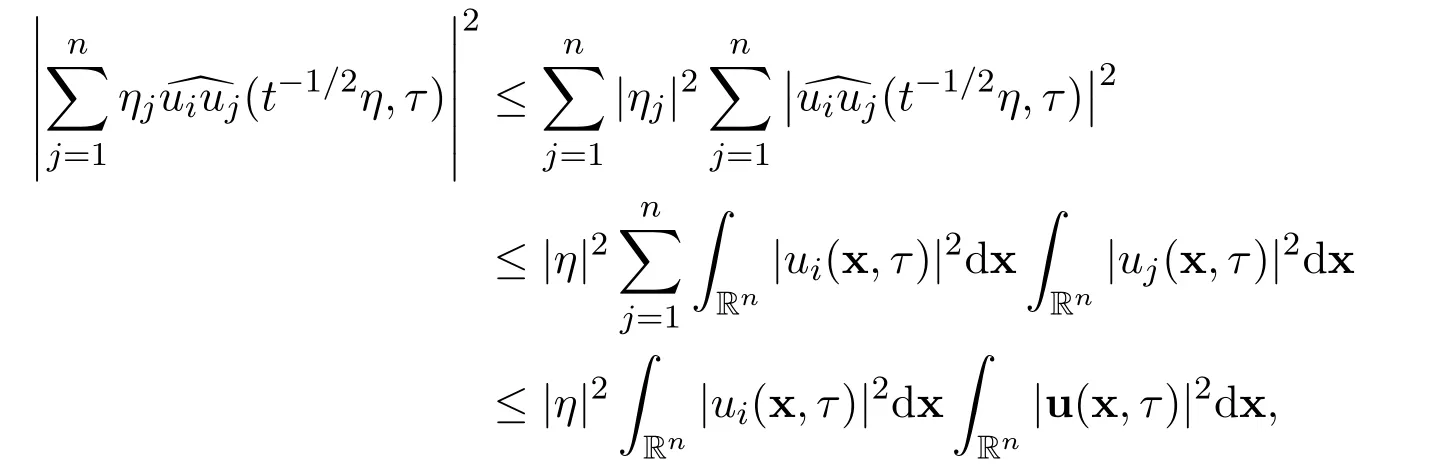
it follows that
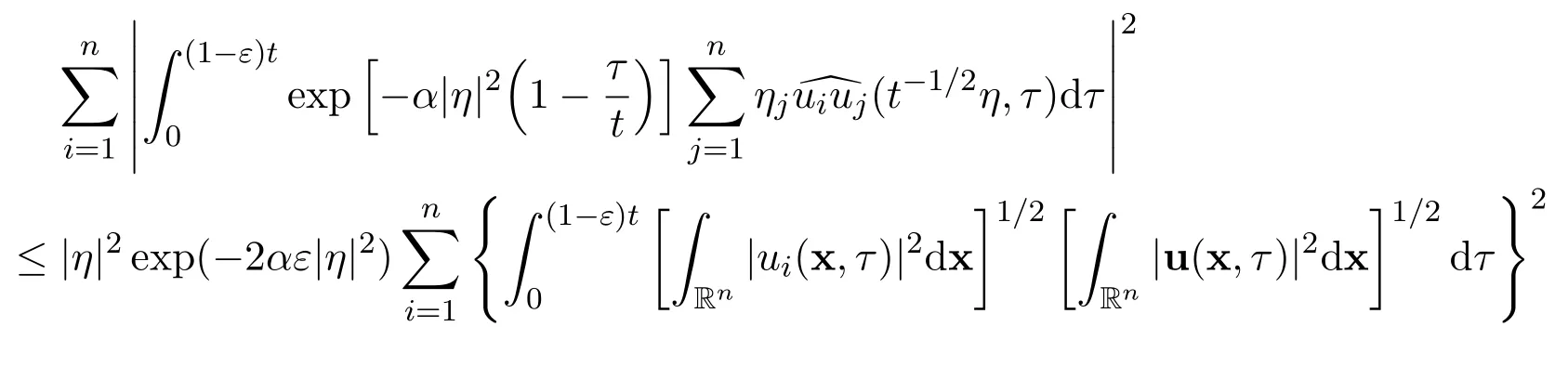

Therefore,there holds the following estimate for the third integral
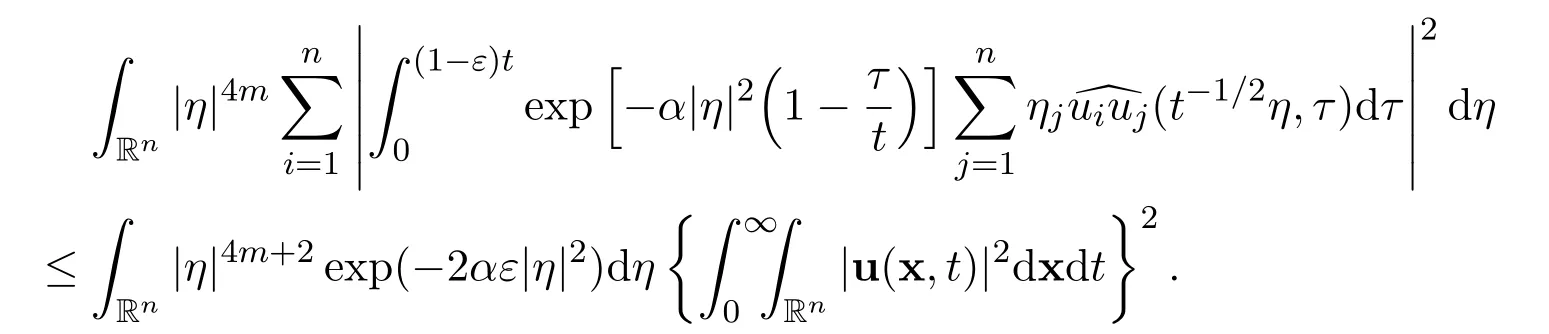
Fourthly,similar to before,note that
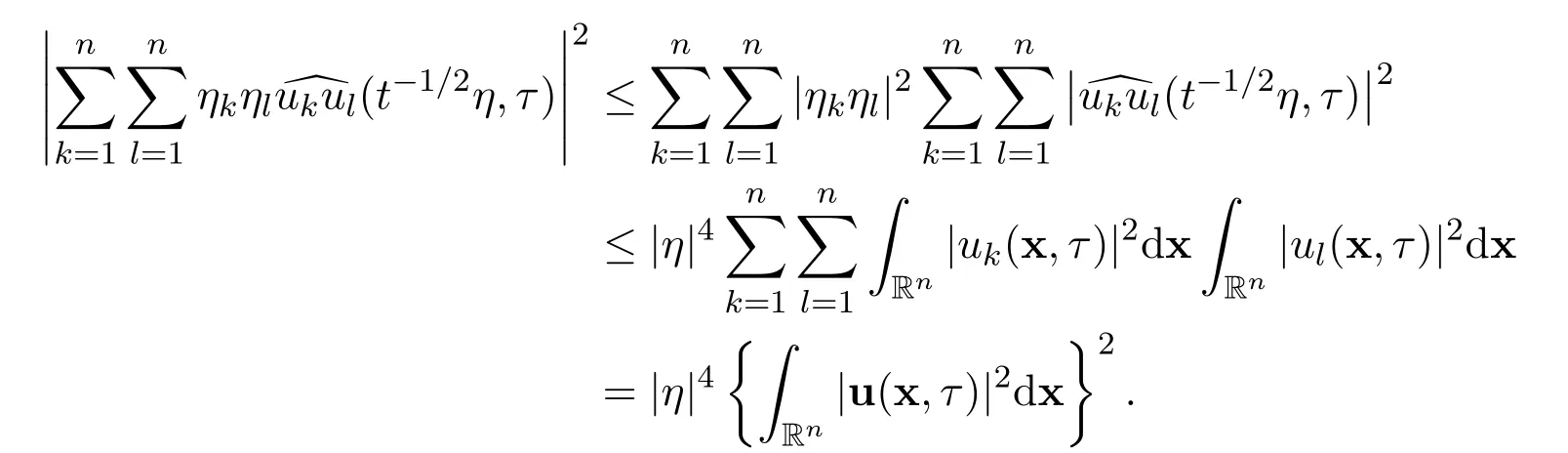
Thus
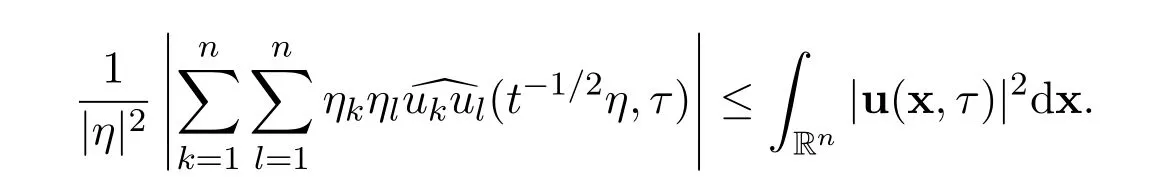
Now we get
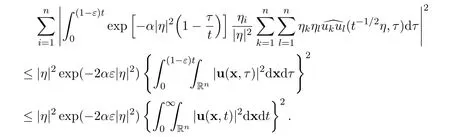
Therefore,there holds the estimate for the fourth integral

Recall that η=t1/2ξ,whereand t>0,we have
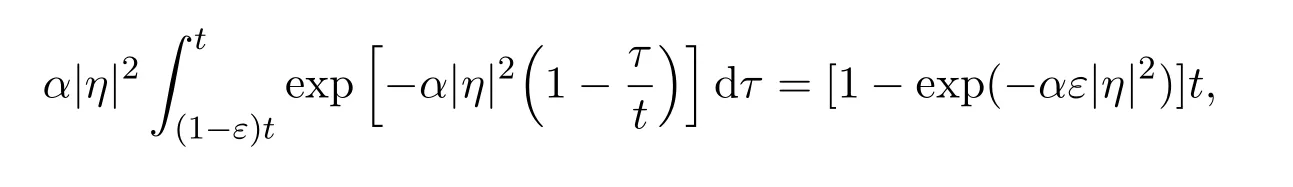
and
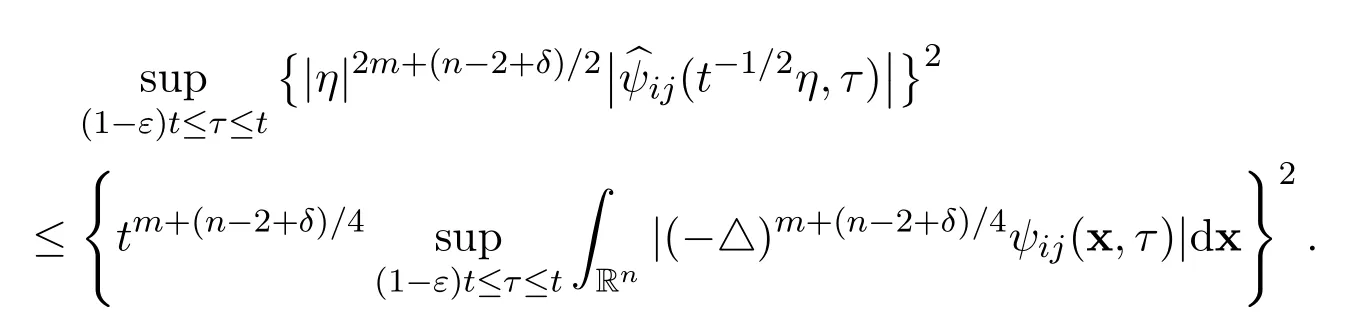
Very similarly
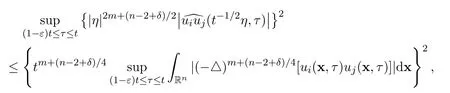
and
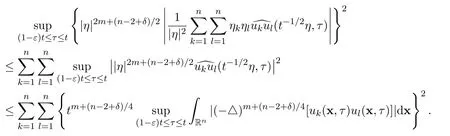
By using these estimates,we arrive at the following estimates
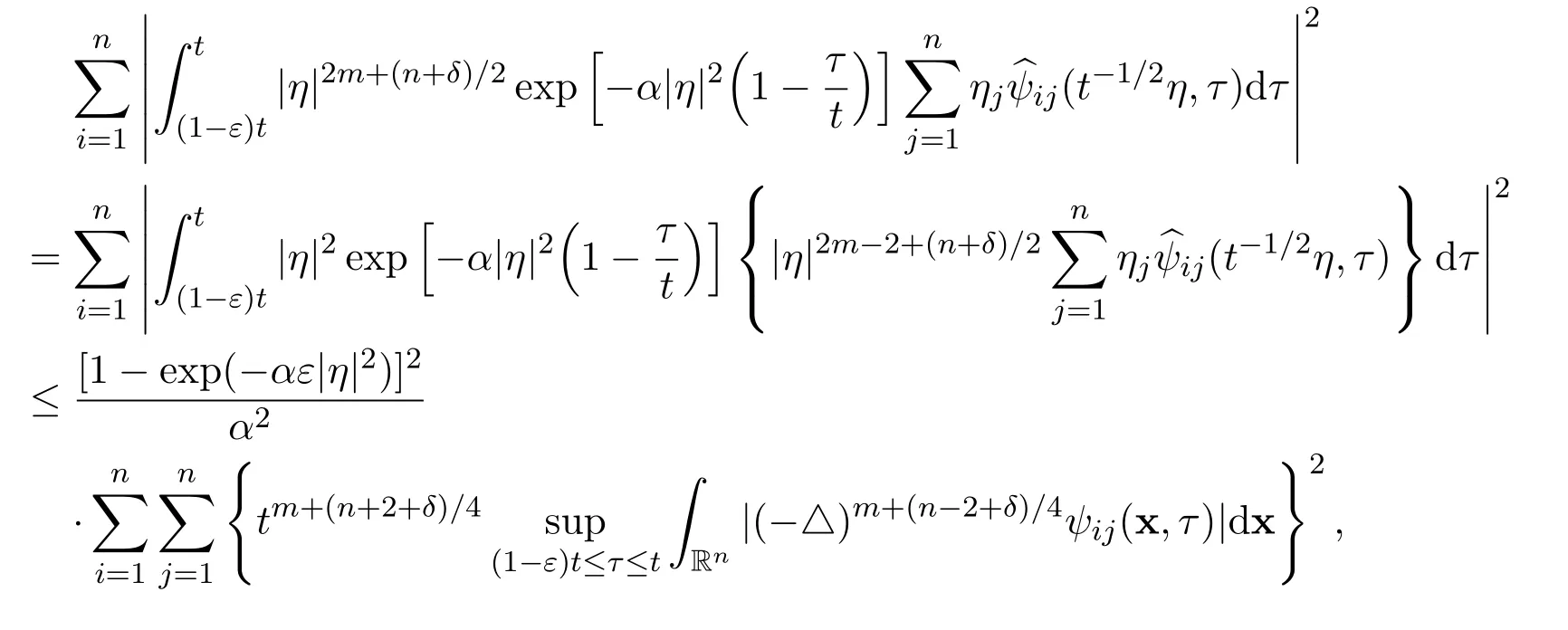
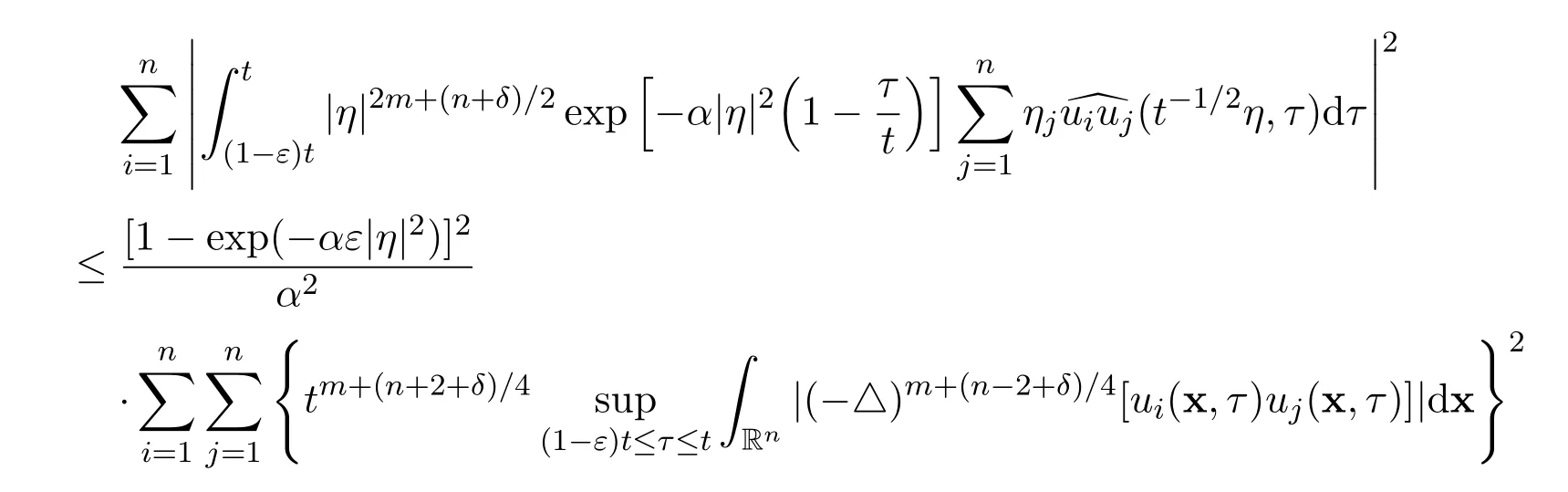
and
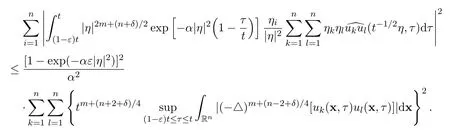
Therefore,there hold the following estimates for the fifth,the sixth and the seventh integrals
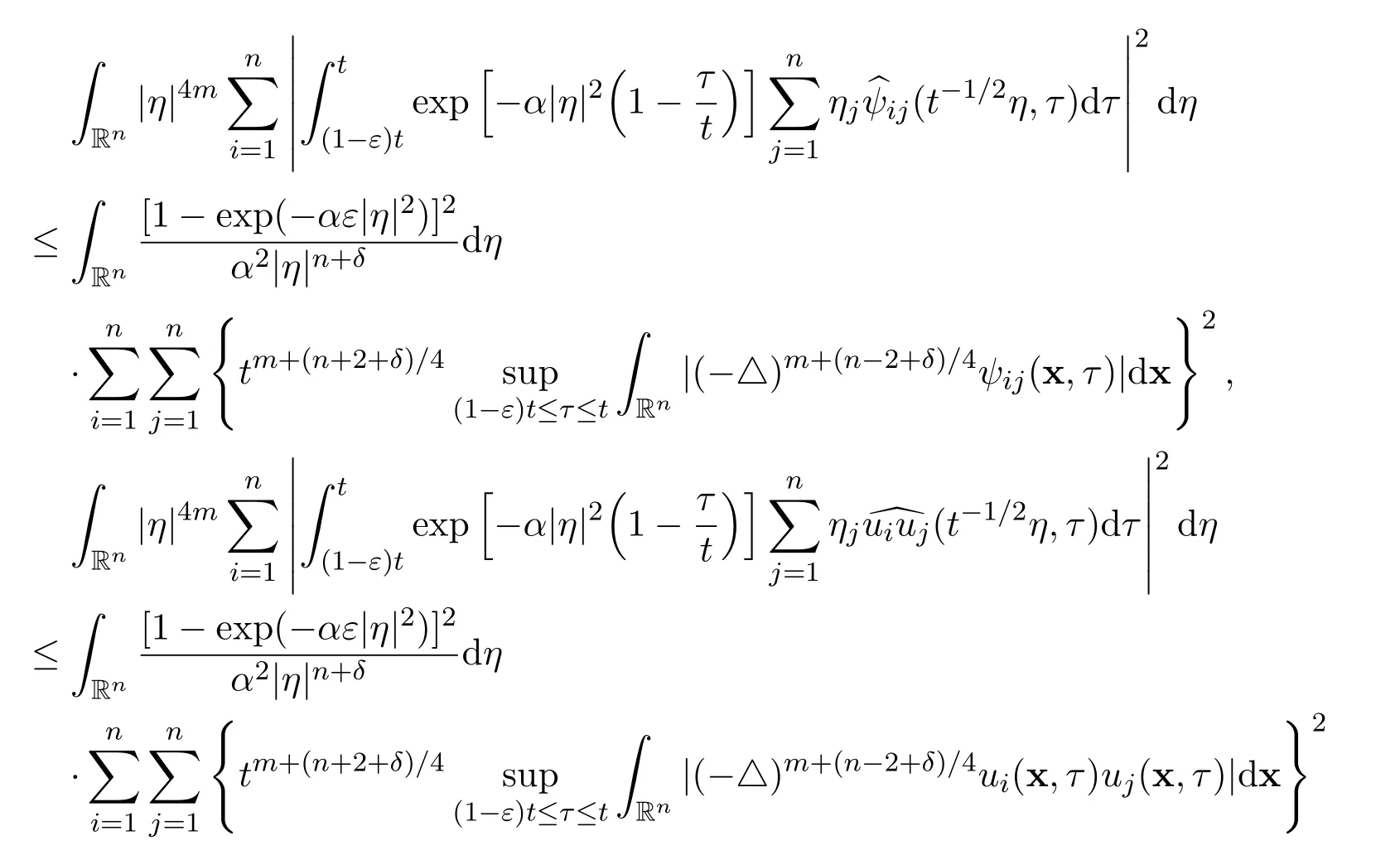
and
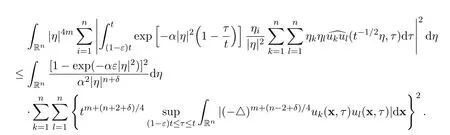
Finally,by coupling together these estimates,the proof of the estimate for
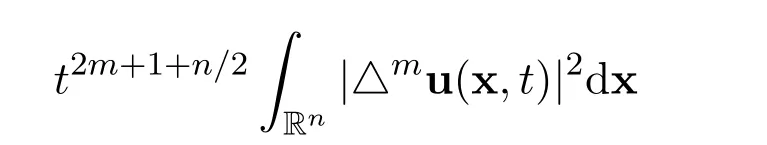
is finished.The proof of the estimate for
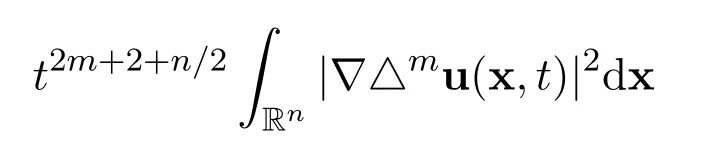
is very similar and it is omitted.The proof of Theorem 1 is finished.
Proof of Theorem 2As before,let u=u(x,t)represent the global smooth solution of the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations.Let v=v(x,t)represent the global smooth solution to the linear heat equation.Let w=w(x,t)=u(x,t)−v(x,t).Then
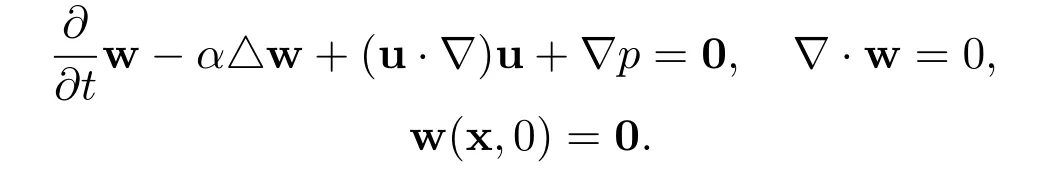
Similar to the above,there holds the following representation for the Fourier transformation
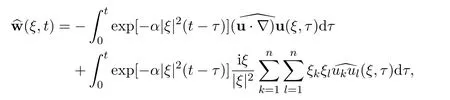
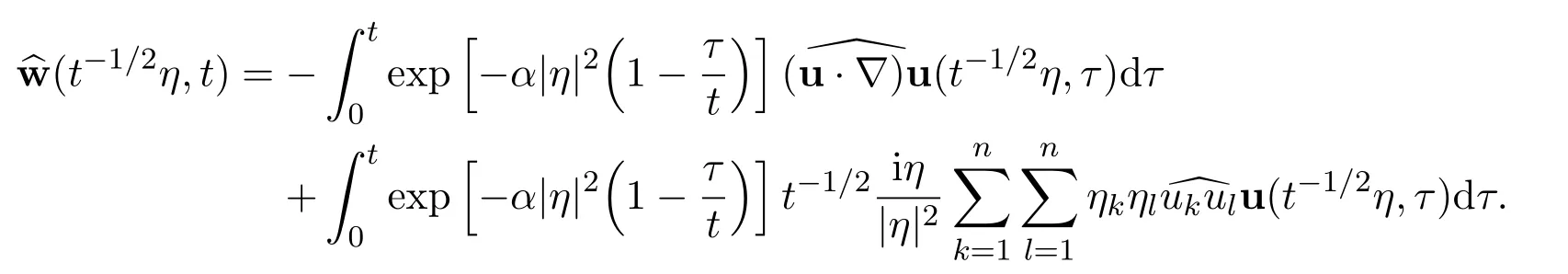
Let us multiply the i-th component ofby t1/2to get
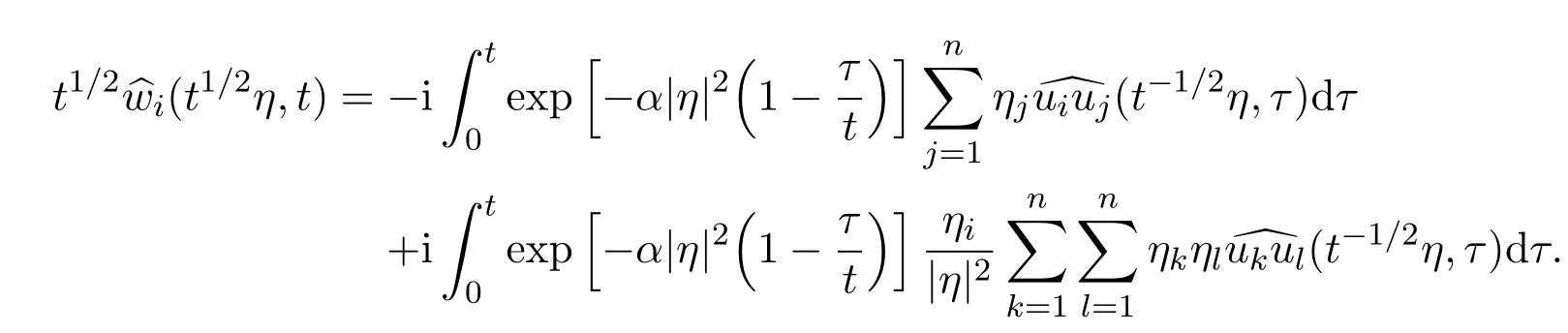
The rest of the proof of Theorem 2 is very similar to that of Theorem 1 and it is omitted.
Definition 3Let 0<ε<1 be a small positive constant.Define

Definition 4Let 0<ε<1 be a small positive constant.Define
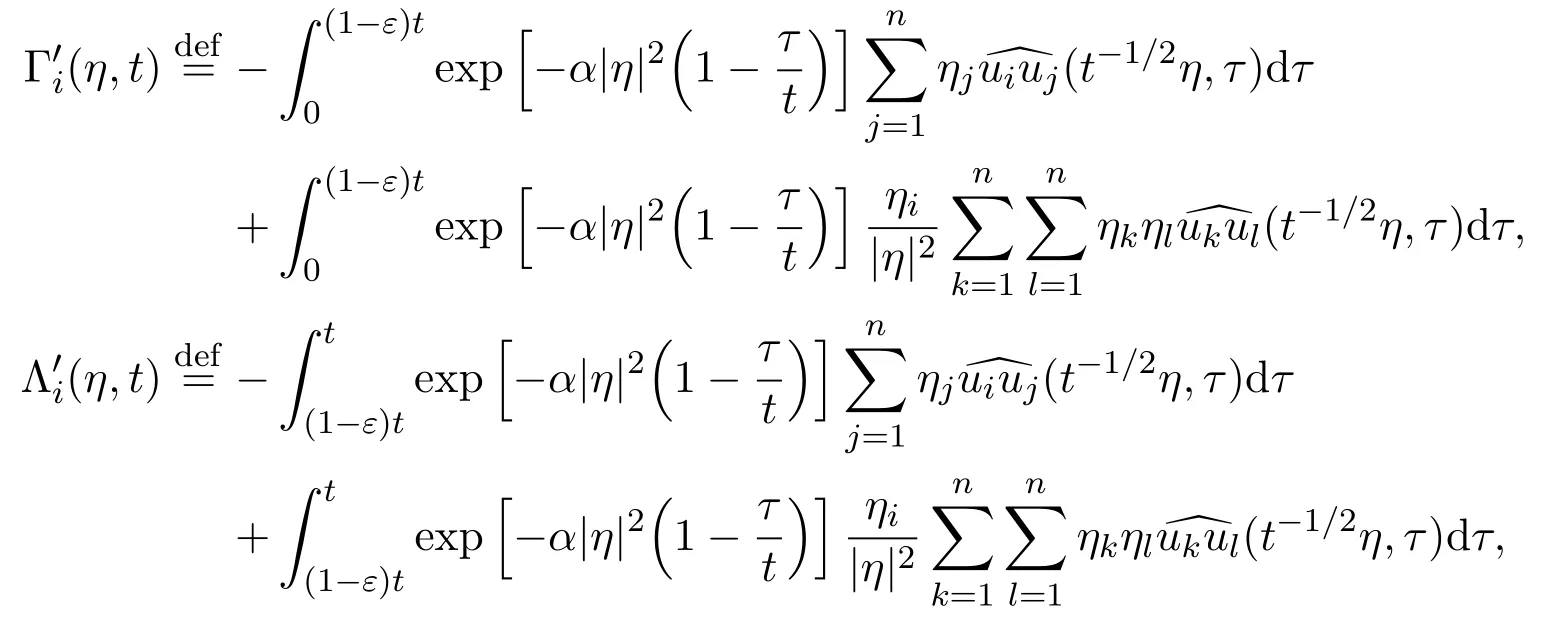
It is easy to see that

and
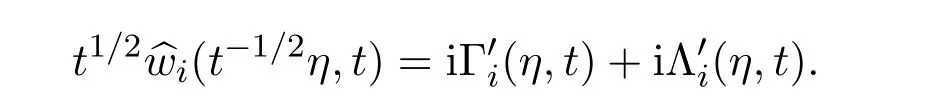
Lemma 5There holds the following result
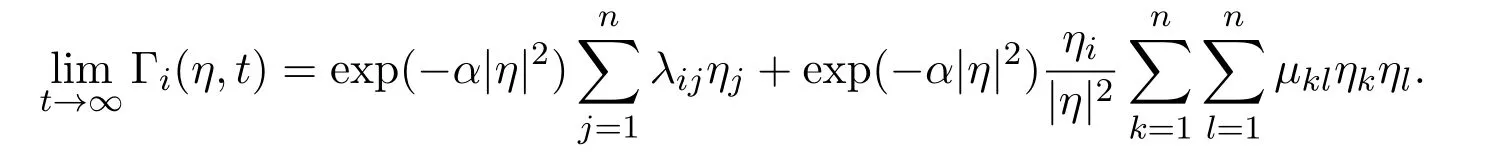
ProofFirst of all,there holds the following estimate
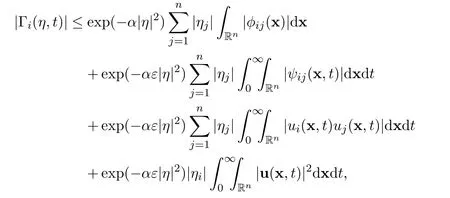
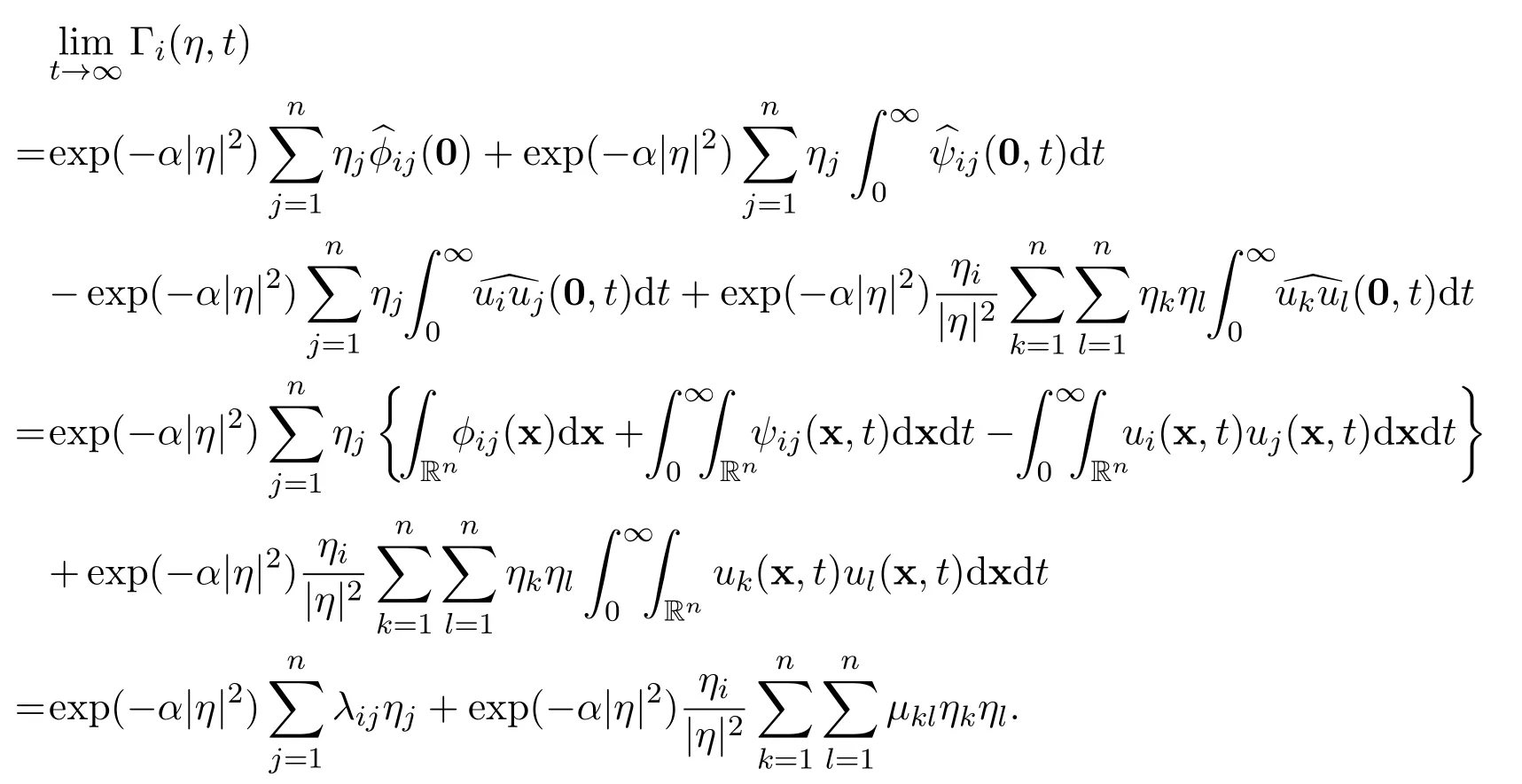
The proof of Lemma 5 is finished.
Lemma 5′There holds the following limit
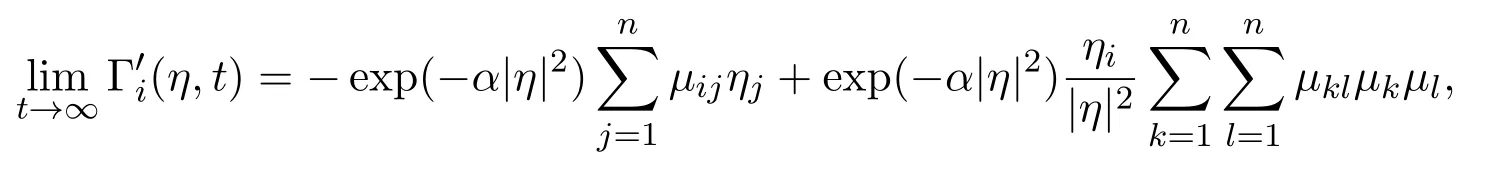
for all i=1,2,3,···,n.
ProofThere holds the following estimate
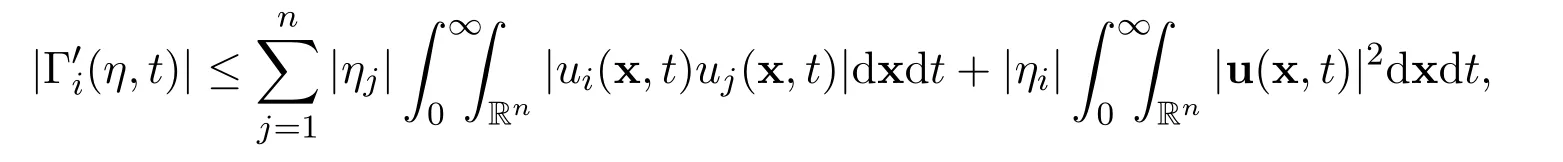
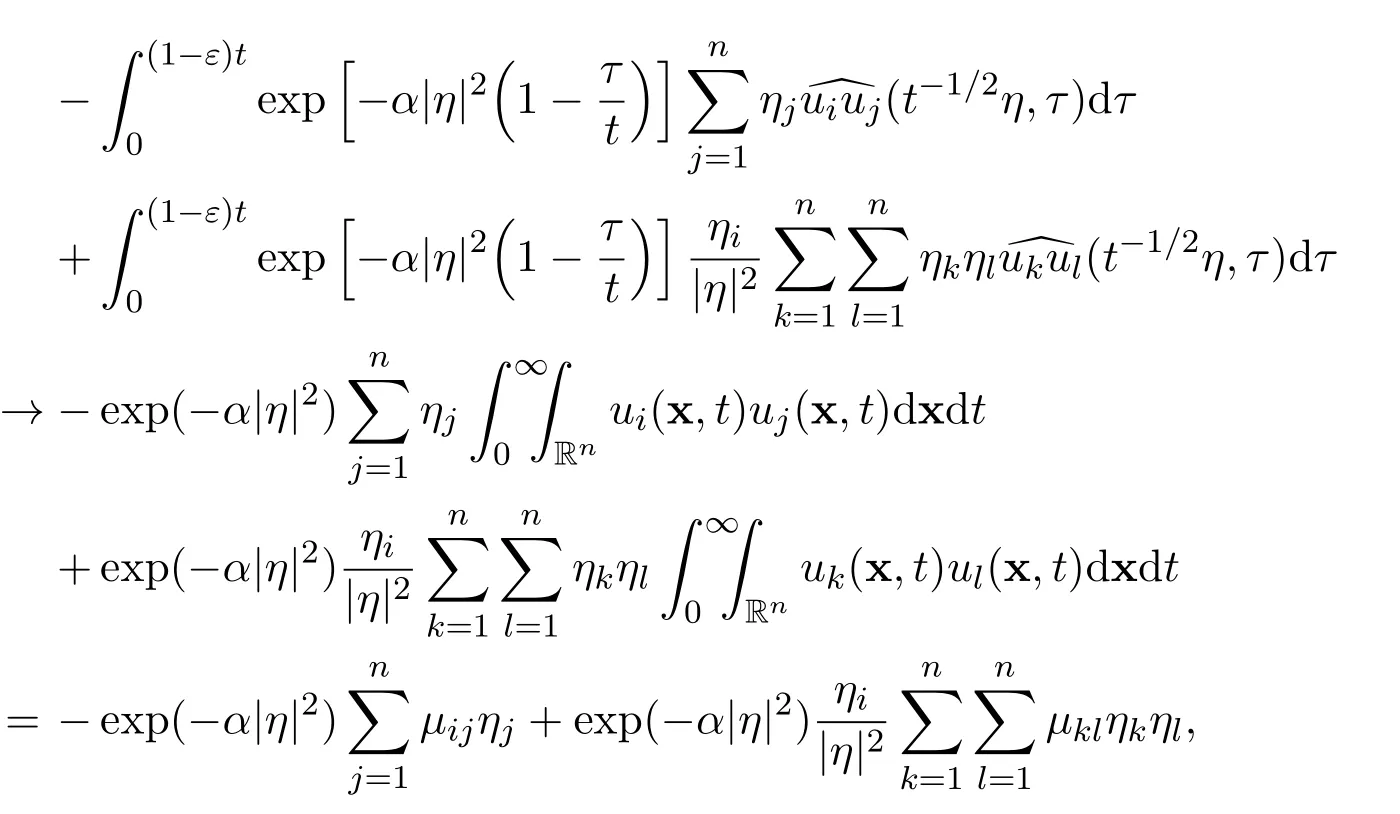
for all i=1,2,3,···,n.The proof of Lemma 5′is finished.
Lemma 6(1)There hold the following estimates
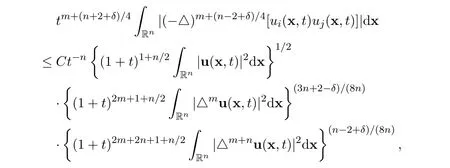
for all positive integers m ≥1 and for all time t>0,where C>0 is a positive constant,independent of u and(x,t).
(2)There hold the following limits

Proof(1)First of all,by using the decay estimate with sharp rate of u and the decay estimates with sharp rates of the derivatives △mu and △m+nu,
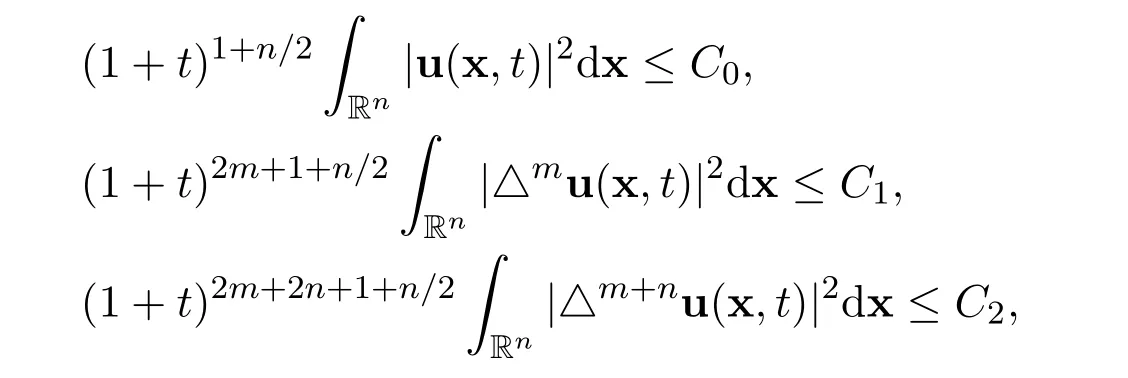
for all positive integers m ≥1 and for all time t>0,where C0>0,C1>0 and C2>0 are positive constants,independent of u and(x,t),we have the following estimates

and
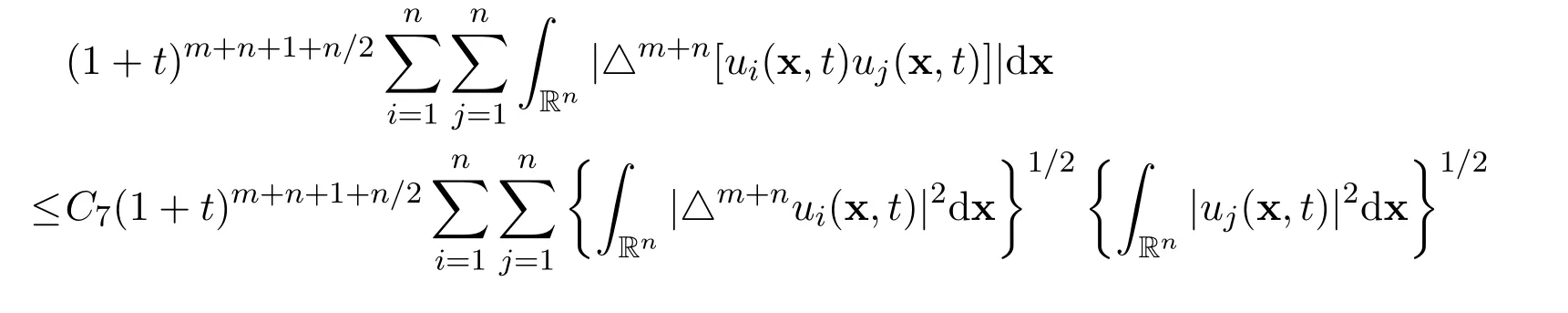

where C3>0,C4>0,···,C9>0 and C10>0 are positive constants,independent of u and(x,t).
Now by using the Gagliardo-Nirenberg’s interpolation inequality,we have the following estimates
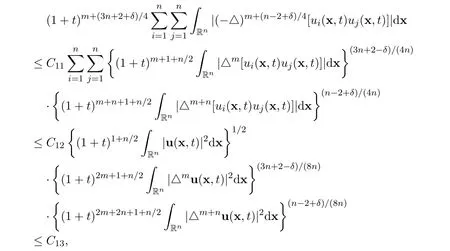
where C11>0,C12>0 and C13>0 are positive constants,independent of u and(x,t).
(2)The exact limits follow from the estimates.The proof of Lemma 6 is completely finished.
Definition 5First of all,define the following real scalar functions
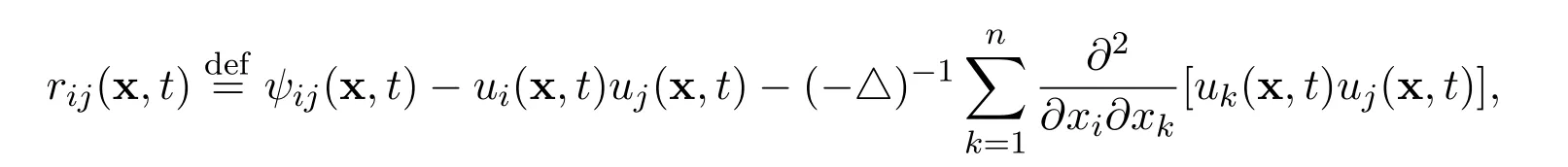
for all i=1,2,3,···,n and j=1,2,3,···,n. Then define the real vector valued function
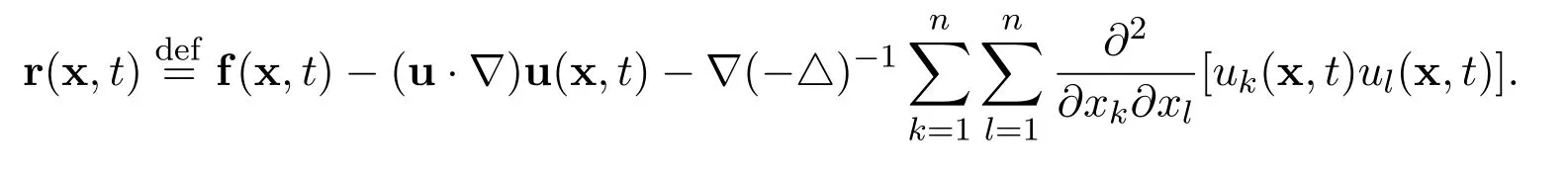
Now we have
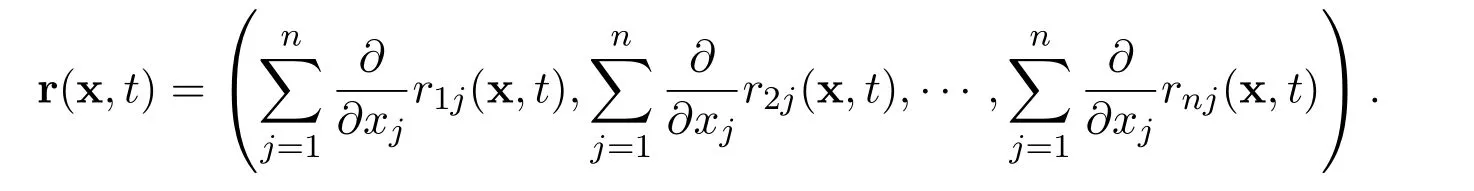
Let m ≥1 be a positive integer.We find

Moreover,we may rewrite
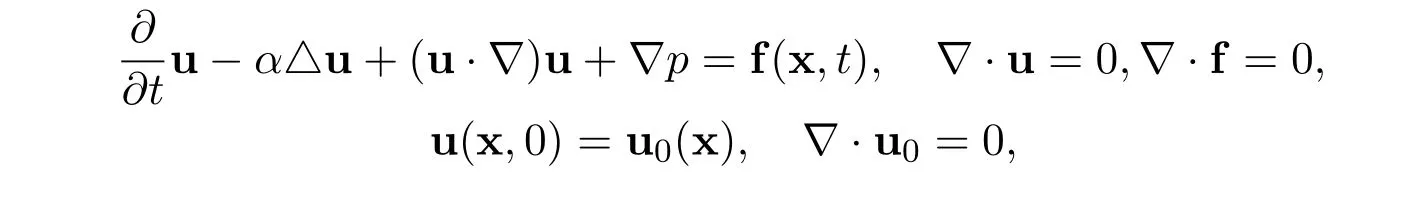
as
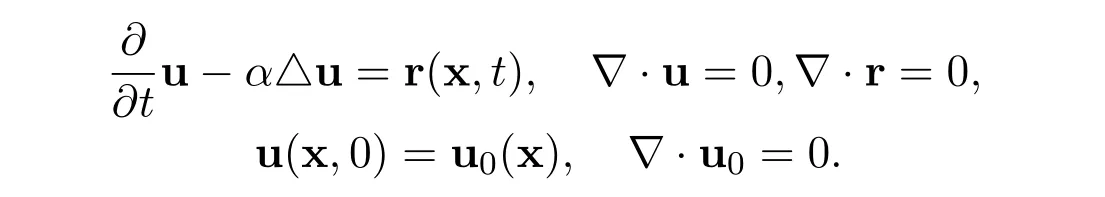
Now we may apply the results for the linear heat equation developed in Subsection 2.1 and the results of Lemmas 5 and 6.
2.3 Precise values of several special integrals
In the proofs of Theorems 3 and 4,we will need the precise values of the following special integrals.
Lemma 7There hold the following results,for all positive integers m ≥1,i=1,2,3,···,n and j=1,2,3,···,n,
(1)
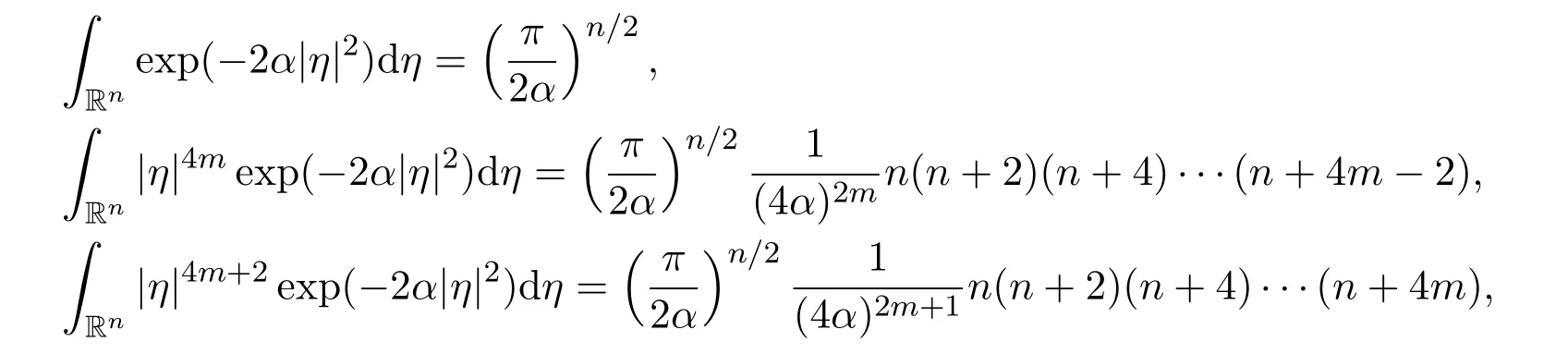
(2)
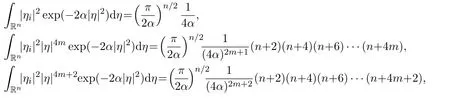
(3)
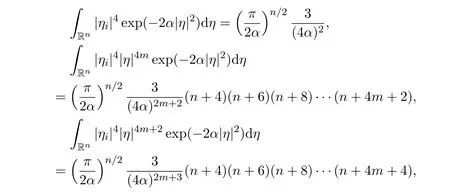
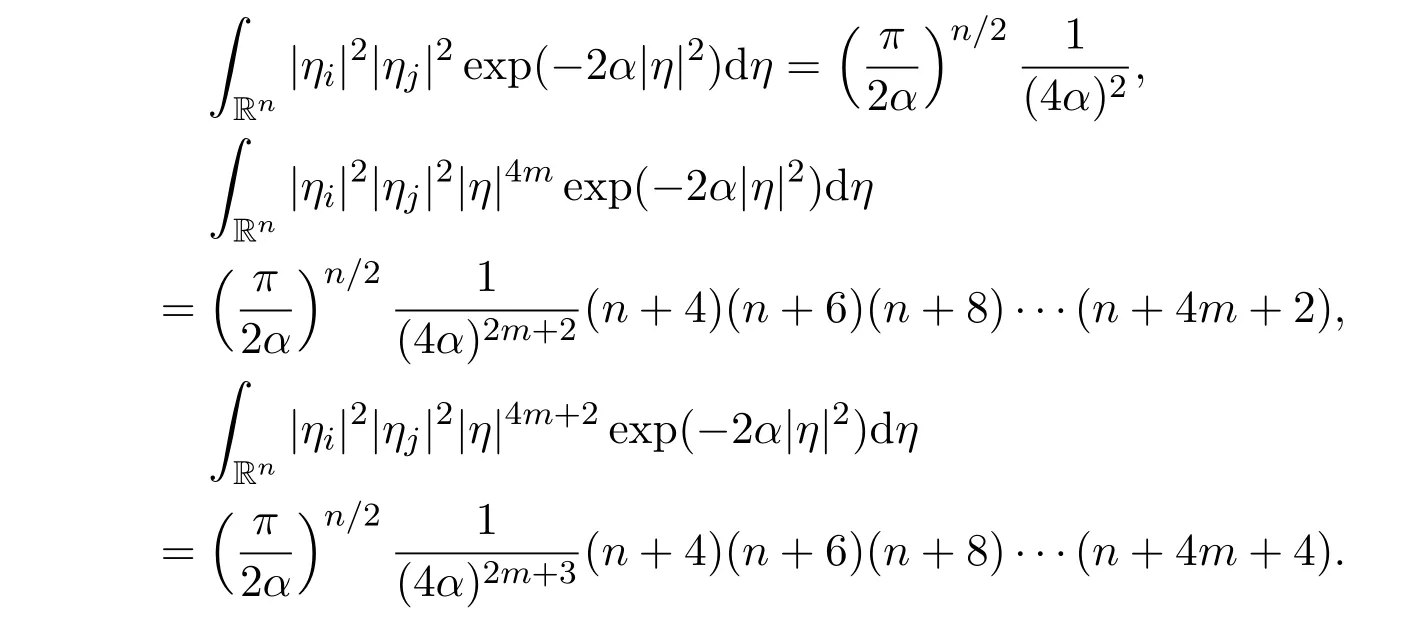
ProofThe ideas in the proof of Lemma 7 are easy but the details may be tedious.The details are omitted.
From Lemma 7,we can immediately obtain the following lemma.
Lemma 8There hold the following results,for all positive integers m ≥1,i=1,2,3,···,n and j=1,2,3,···,n,with ij,
(1)

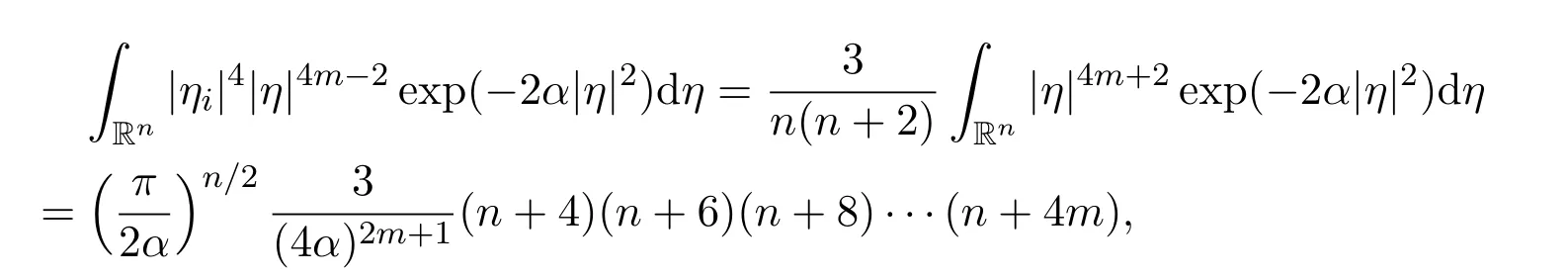
(2)
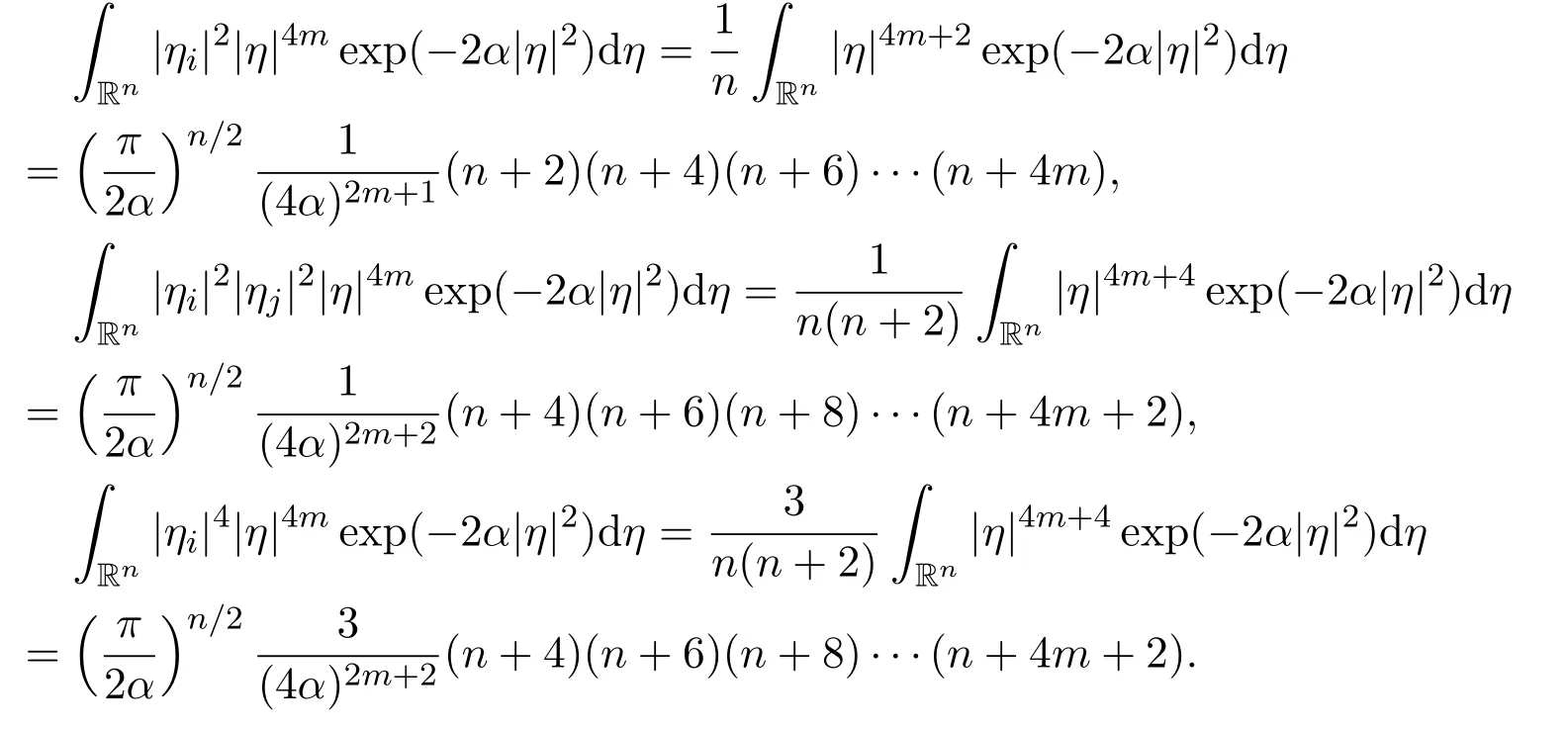
There are some kind of symmetry in these integrals because the results are independent of the positive integers i=1,2,3,···,n and j=1,2,3,···,n.
Lemma 9Let the positive integer n ≥2. Let{λij:i=1,2,3,···,n,j=1,2,3,···,n},{µij:i=1,2,3,···,n,j=1,2,3,···,n}be two sets of real constants,such thatµij=µji,for all positive integers i=1,2,3,···,n and j =1,2,3,···,n.Then there hold the following results
(1)
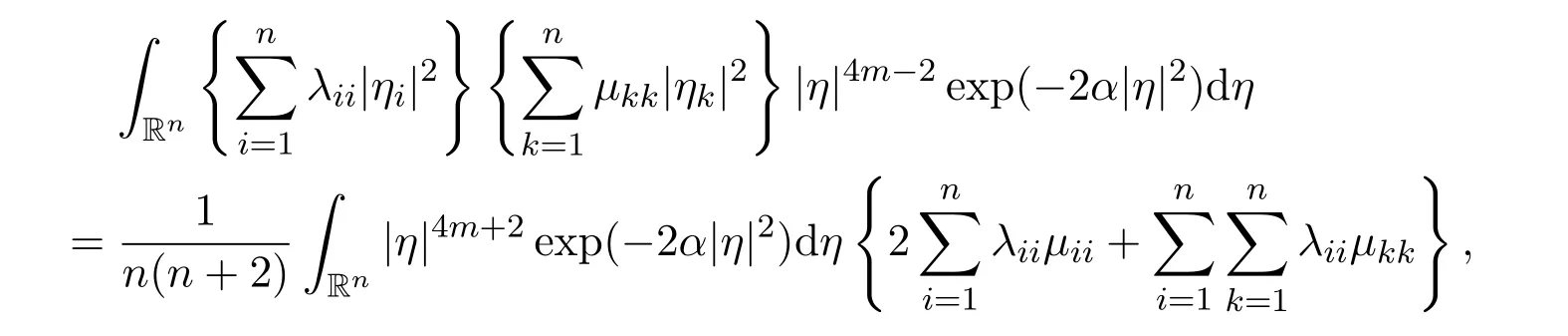
(2)
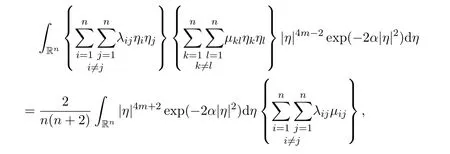
(3)
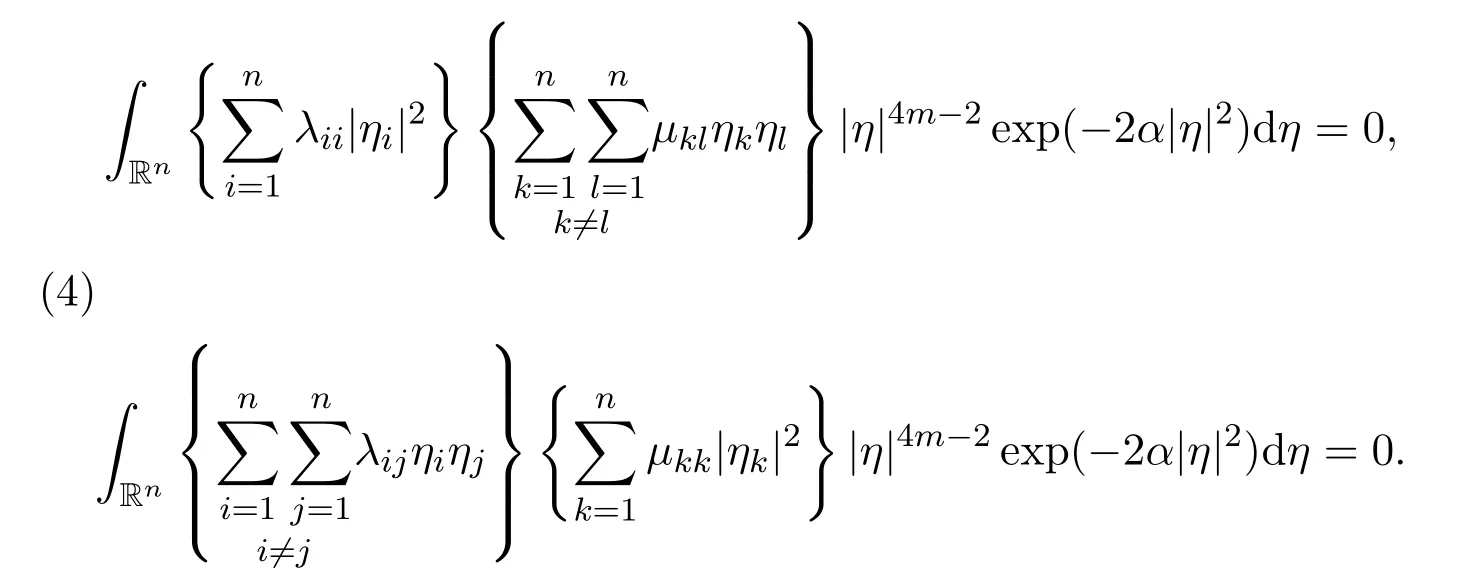
ProofFirst of all,we have
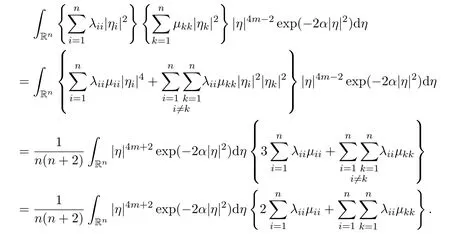
Secondly,we have
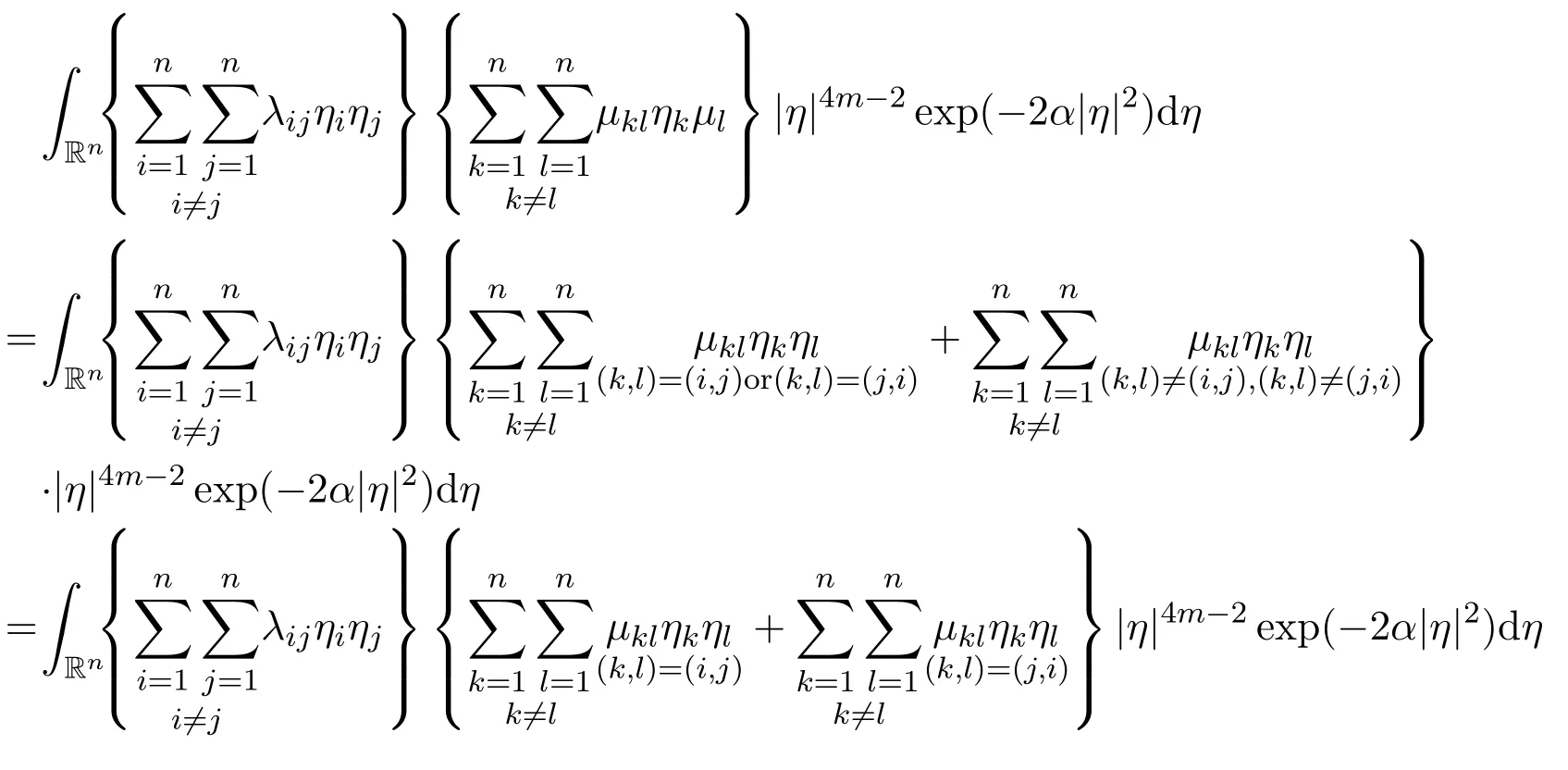
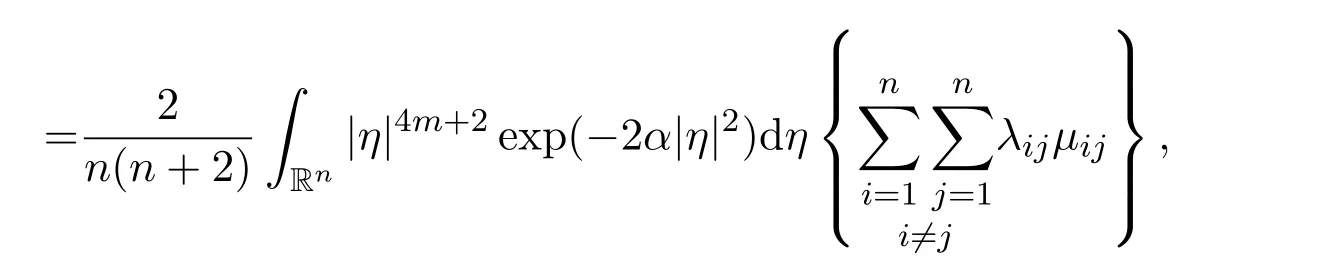
where

Note that
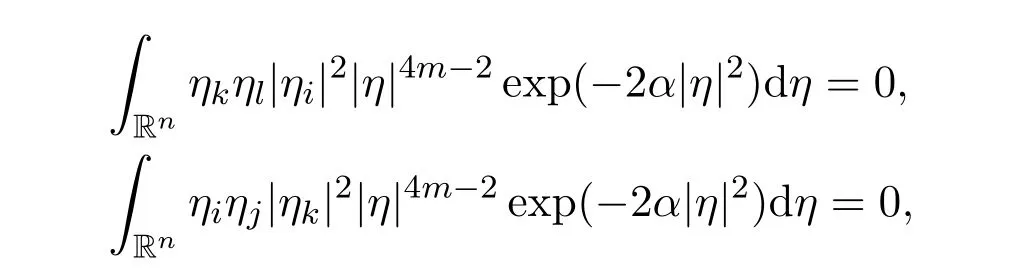
for all i=1,2,3,···,n,j=1,2,3,···,n,k=1,2,3,···,n and l=1,2,3,···,n,with i ̸j and kl. Now the proofs of(3)and(4)are very easy. The proof of Lemma 9 is completely finished now.
Lemma 10Let

be two sets of real constants,such thatµij=µji,for all positive integers i=1,2,3,···,n and j=1,2,3,···,n. Then there hold the following results,for all positive integers m ≥1,(1)
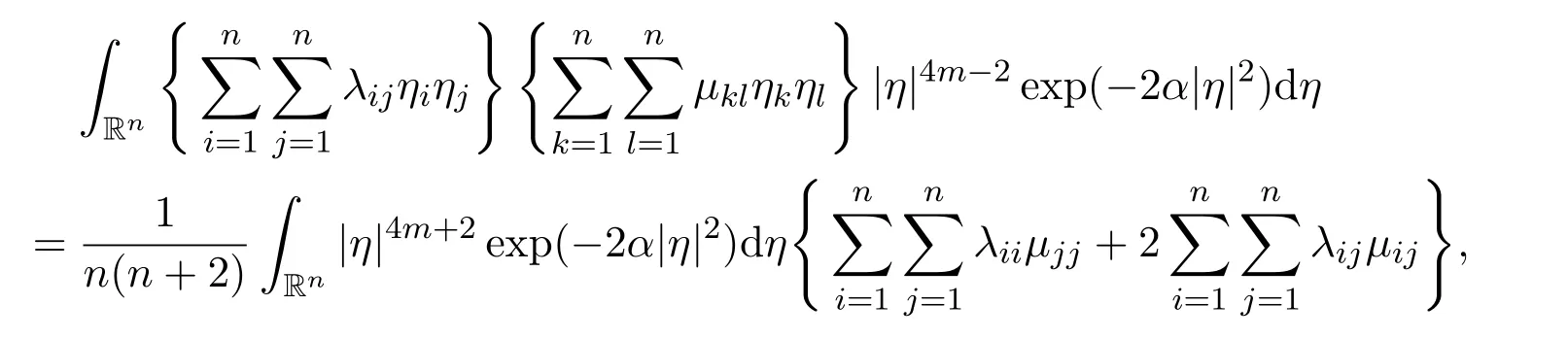
(2)
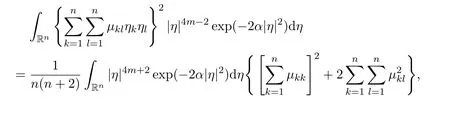
(3)
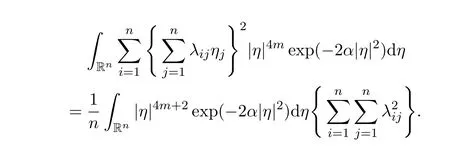
ProofFirst of all,by using very simple computations,we have

Then,by using Lemma 9,we have the following computations
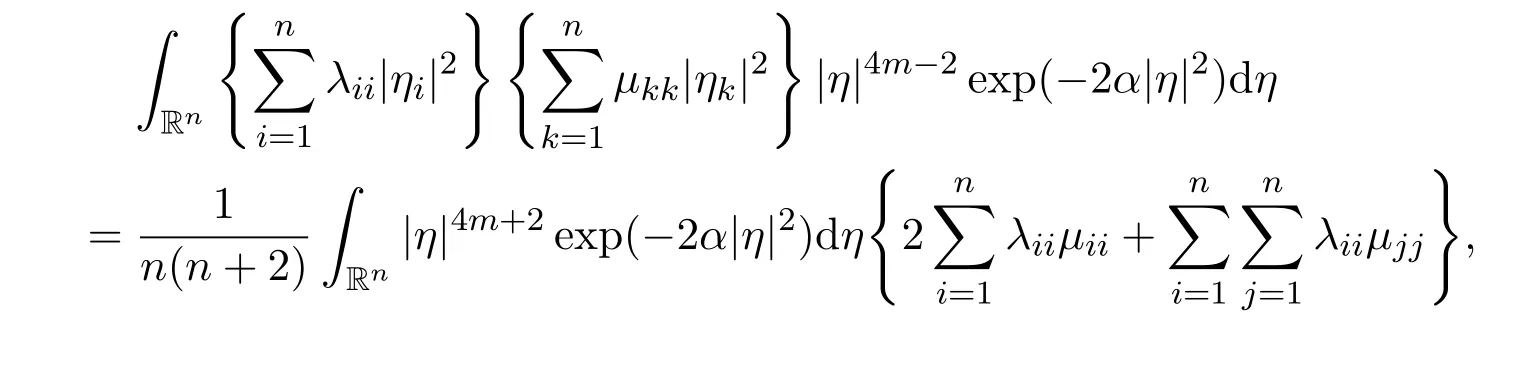
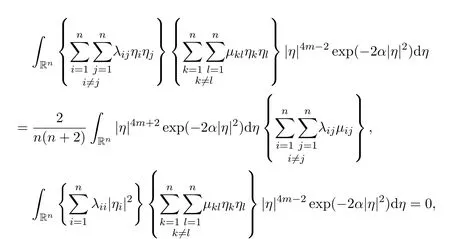
and
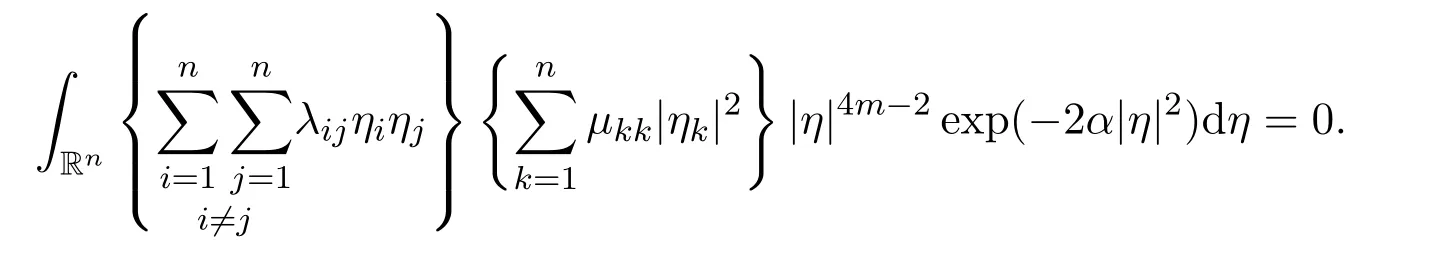
Therefore,by coupling together these results,we have
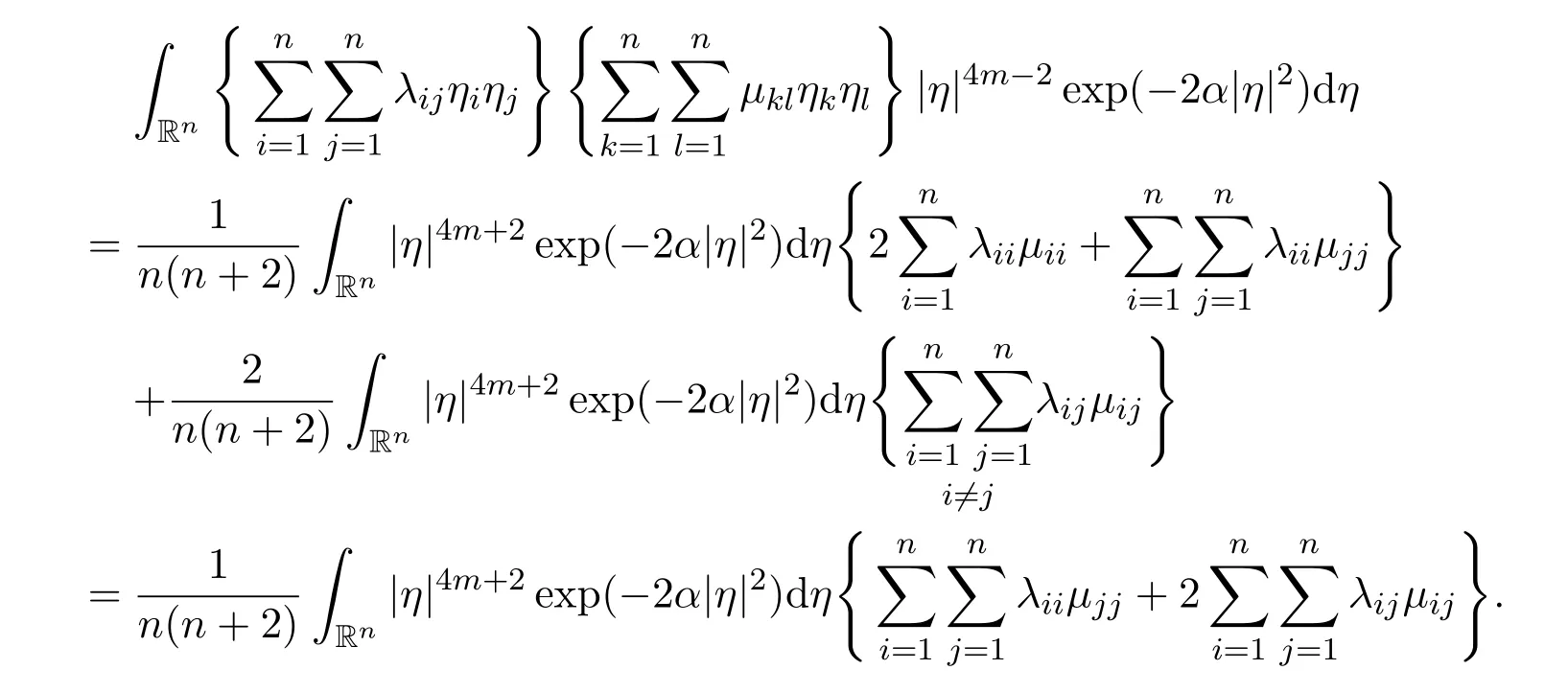
The second result follows from the first result. Now let us prove the third result.We have
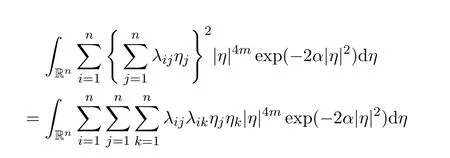
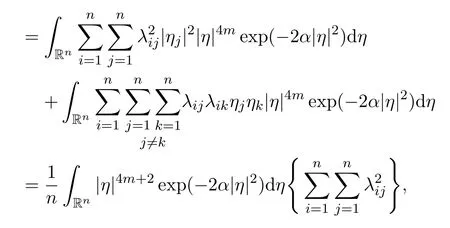
where

The proof of Lemma 10 is finished.
2.4 Completion of the proofs of the main theorems
The main purpose of this subsection is to make complete use of the technical lemmas to finish the proofs of the exact limits of the global smooth solution of the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations.
First of all,let us prove Theorem 3.As before,define the following three sets of real numbers
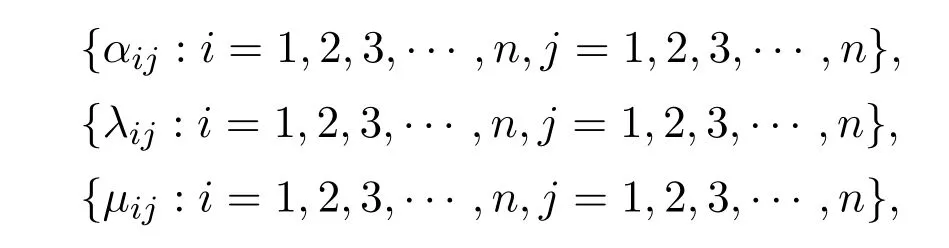
by
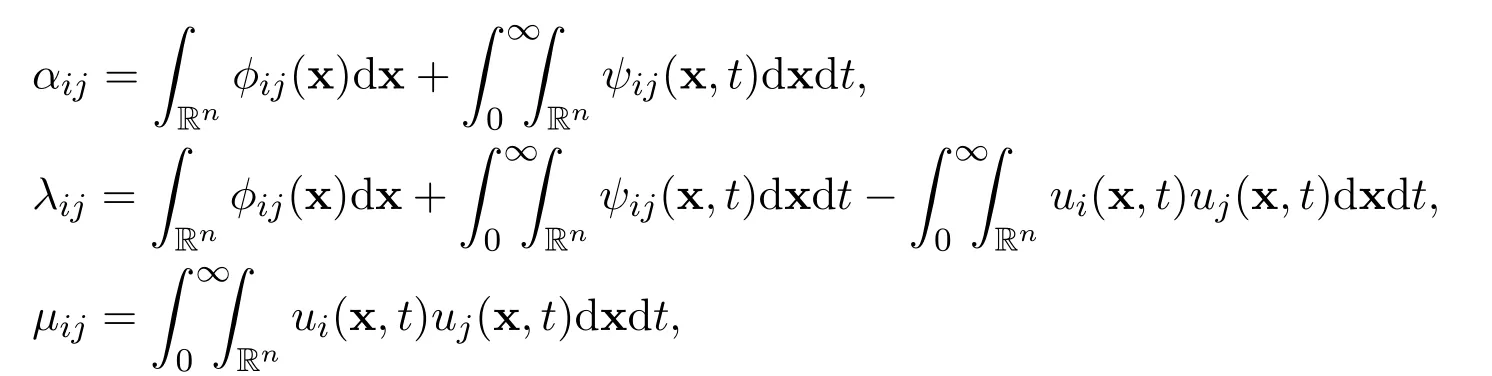
for all positive integers i=1,2,3,···,n and j=1,2,3,···,n. Obviously,αij=λij+µijandµij=µji.
Recall that there holds the following decay estimate

for all time t>0,where C>0 is a positive constant,independent of u and(x,t).Therefore,the existence of the following integrals are guaranteed
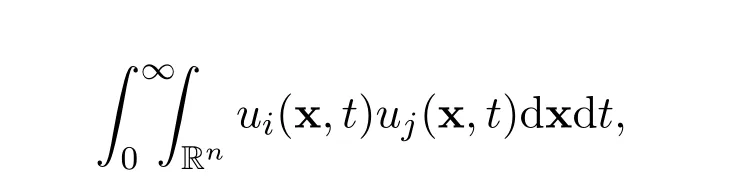
for all i=1,2,3,···,n and j=1,2,3,···,n.
Lemma 11Let m ≥1 be a positive integer.There holds the following result

ProofBy using Lemma 10,we have the following computations

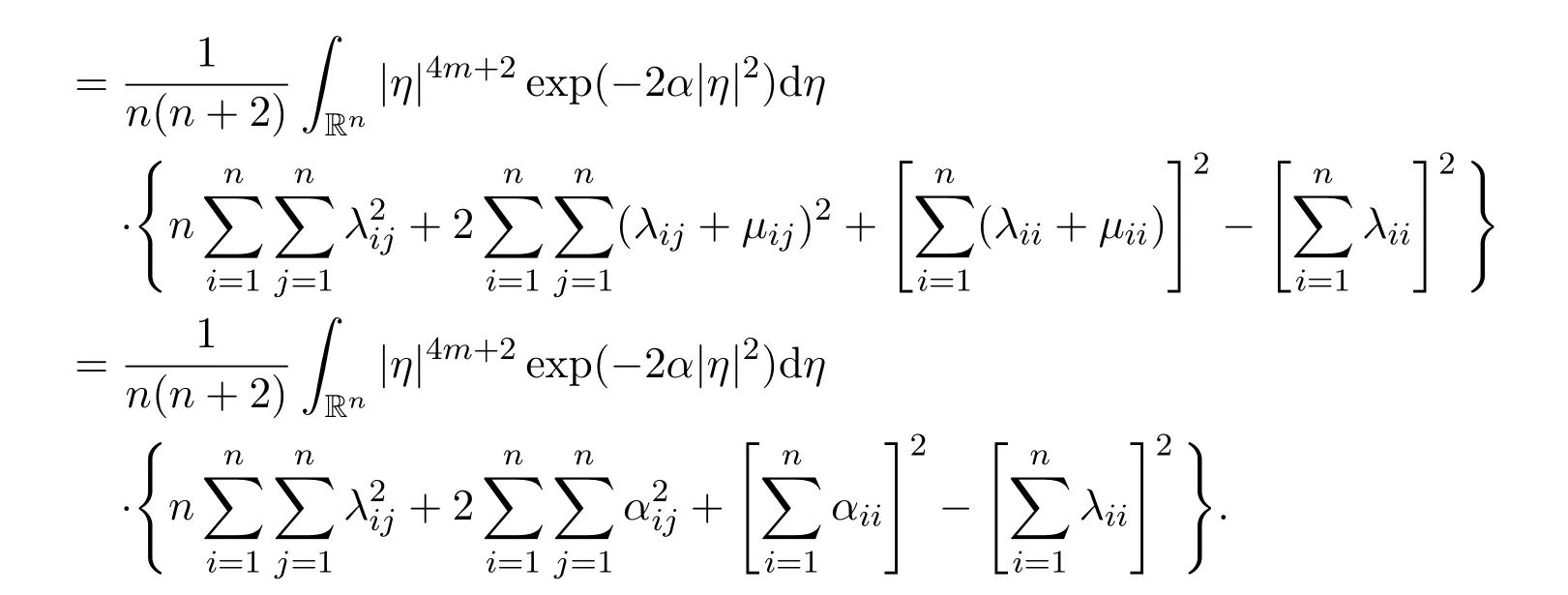
The proof of Lemma 11 is finished.
Lemma 12There holds the following result
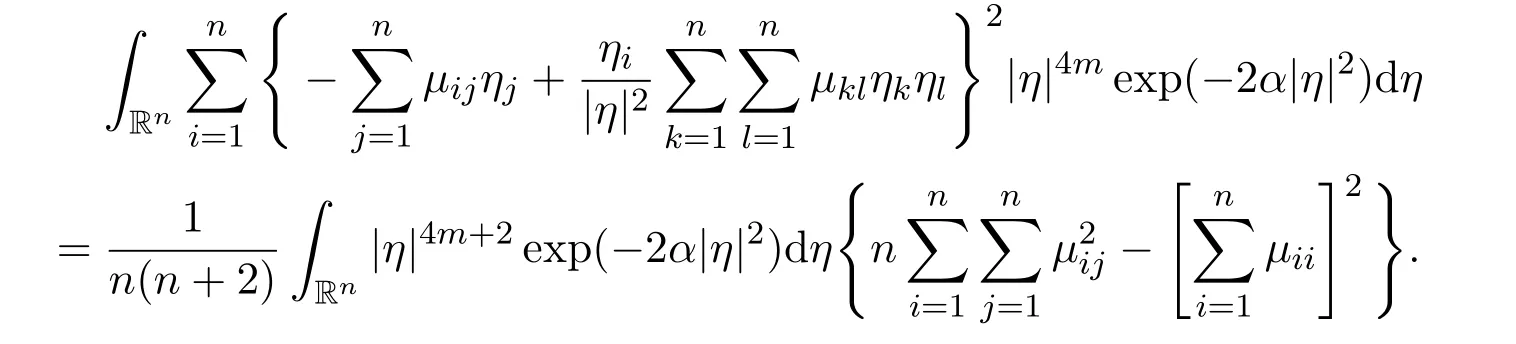
ProofAs before,by using Lemma 10,we have the following computations

The proof of Lemma 12 is finished.
Proof of Theorem 3By coupling together the results of Lemma 5,Lemma 6,Lemma 11 and Theorem 6,the proof is completed.
Proof of Theorem 4By coupling together the results of Lemma 5′,Lemma 6,Lemma 12 and Theorem 6,the proof is finished.
Therefore,the proofs of the exact limits in Theorems 3 and 4 are finished.
3 Conclusions and Remarks
3.1 Summary
Consider the n-dimensional incompressible Navier-Stokes equations. Let the initial functionand the external force f ∈Then there exists a global weak solution.The global weak solutions become sufficiently small and sufficiently smooth after a long time,see[7]. Therefore,the mathematical analysis and results are rigorously true for all large time t ≥T.
Without loss of generality,suppose that there hold the following uniform energy estimates

for all t>0,where C0>0,C1>0,C2>0,C3>0 and C4>0 are positive constants,independent of u and(x,t).
Then there hold the decay estimates with sharp rates
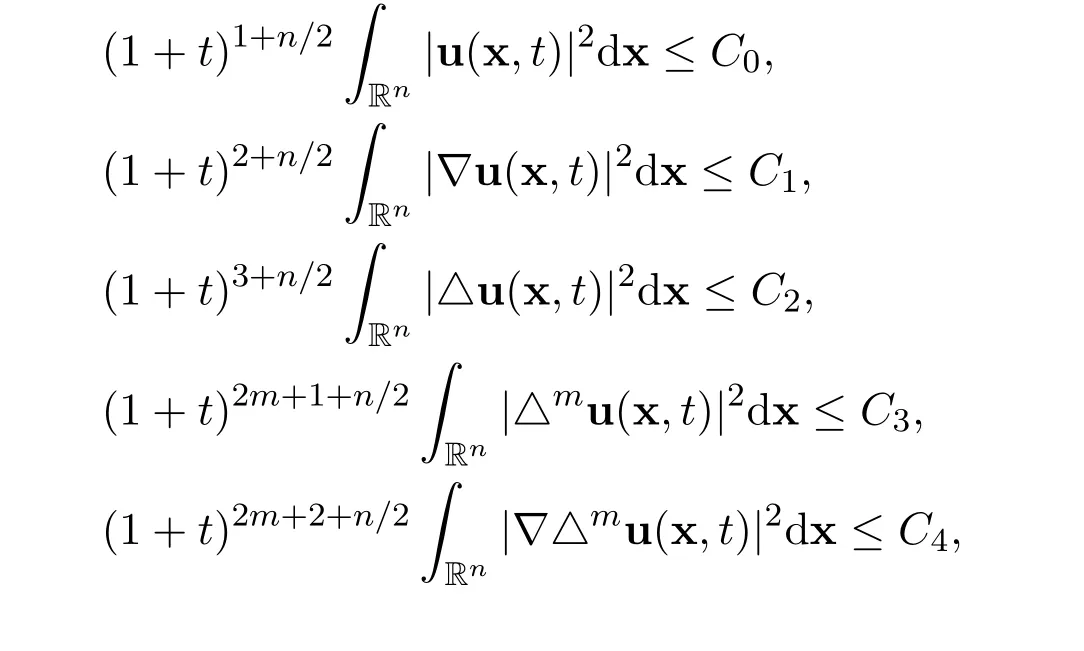
for all time t>0,where C0>0,C1>0 C2>0,C3>0 and C4>0 are positive constants,independent of u and(x,t).
By coupling together several important traditional ideas(Fourier transformation,Parseval’s identity,Lebesgue’s dominated convergence theorem,Gagliardo-Nirenberg’s interpolation inequality),existing results(the existence of the global weak solutions,the existence of the local smooth solution and the decay estimates with sharp rates)and new idea(more appropriate coupling of existing methods and results),we have developed a new method to establish the estimates
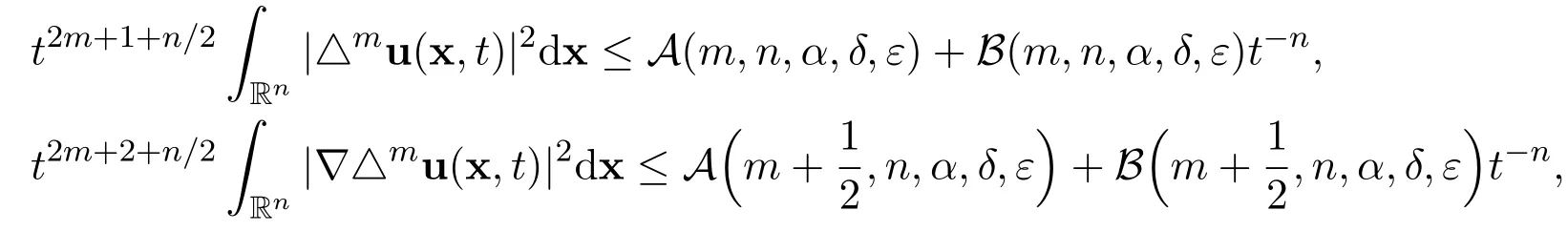
and
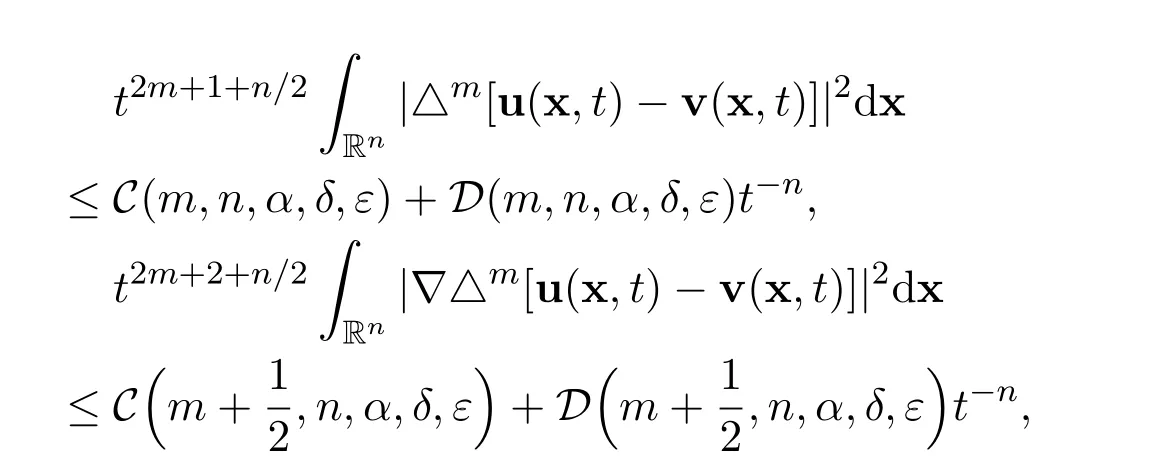
for all positive integers m ≥1 and for all sufficiently large time t ≥T,and to accomplish the exact limits
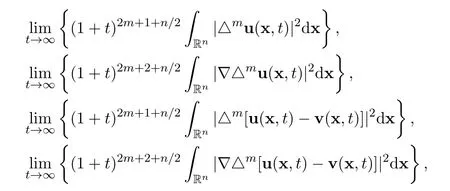
in terms of α,m,n and the following integrals
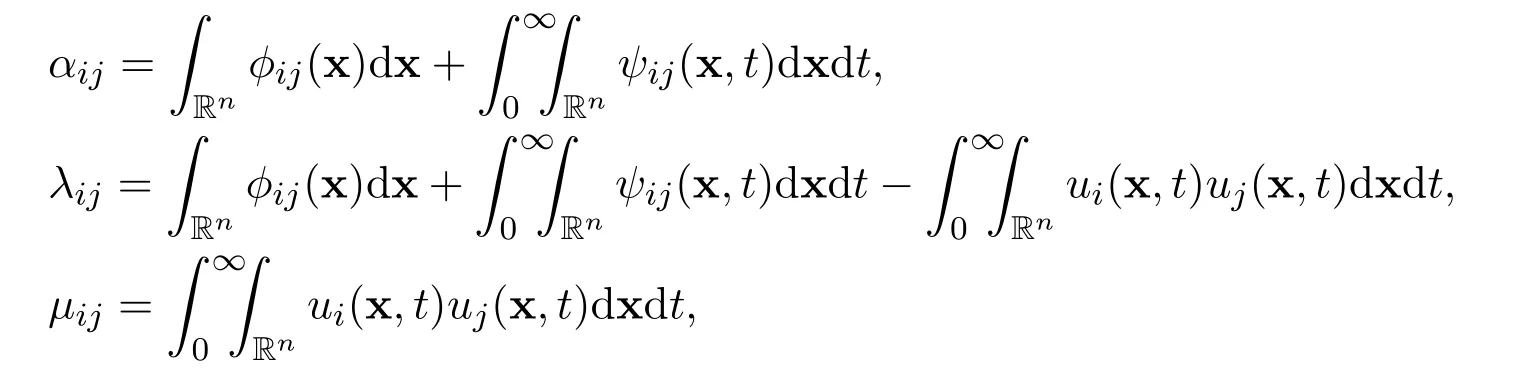
for all positive integers i=1,2,3,···,n and j=1,2,3,···,n.
3.2 Remarks
There are many remarks to the main results.
Remark 5If
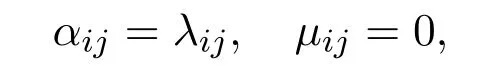
for all i=1,2,3,···,n and j=1,2,3,···,n,then
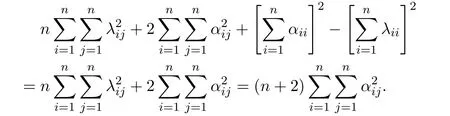
That means that the exact limits of the global smooth solution to the Navier-Stokes equations reduce to those of the global smooth solution to the linear heat equation,if we drop the nonlinear terms(u·∇)u and ∇p.
Remark 6The exact limits are increasing functions of the order m of the derivative and the dimension n,they are decreasing functions of the diffusion coefficient α.Let us consider more carefully the contributions made by various terms to the exact limit of the energy
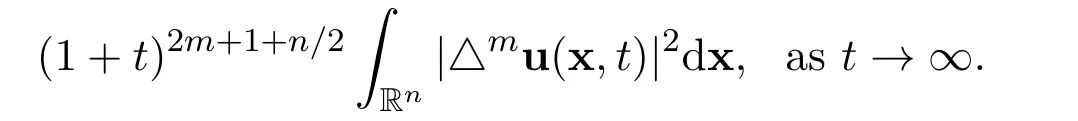
The contributions made by the initial function and the external force are represented by αij,the contributions made by the nonlinear functions(u·∇)u and ∇p are represented byµij.Let
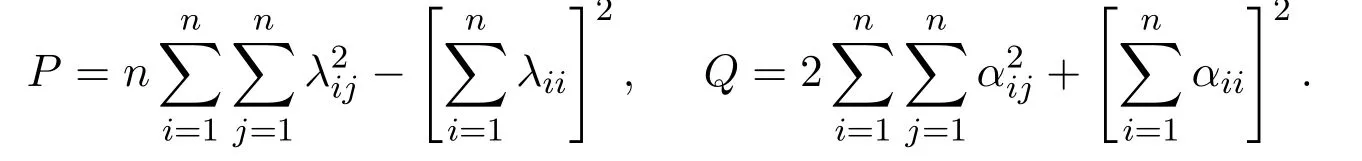
The exact limits are increasing functions of P and Q. Compared with the heat equation,the nonlinear functions(u·∇)u and ∇p make the exact limits larger.
As the order of the derivative increases,the value of the corresponding exact limit may also increase.This motivates the next definition.
Definition 6Define the following ratios

They measure how fast the values of the exact limits increase as the order of the derivative increases.Note that
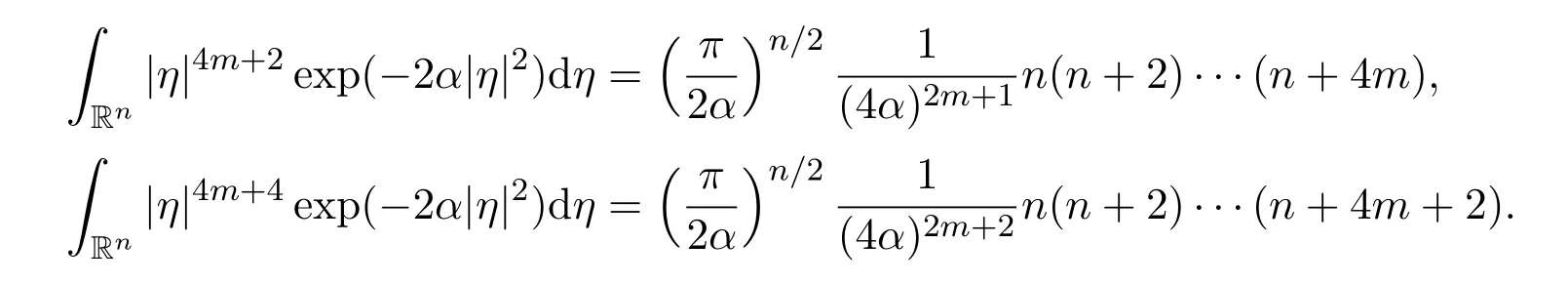
Remark 7For the global smooth solution of the linear heat equation,we have
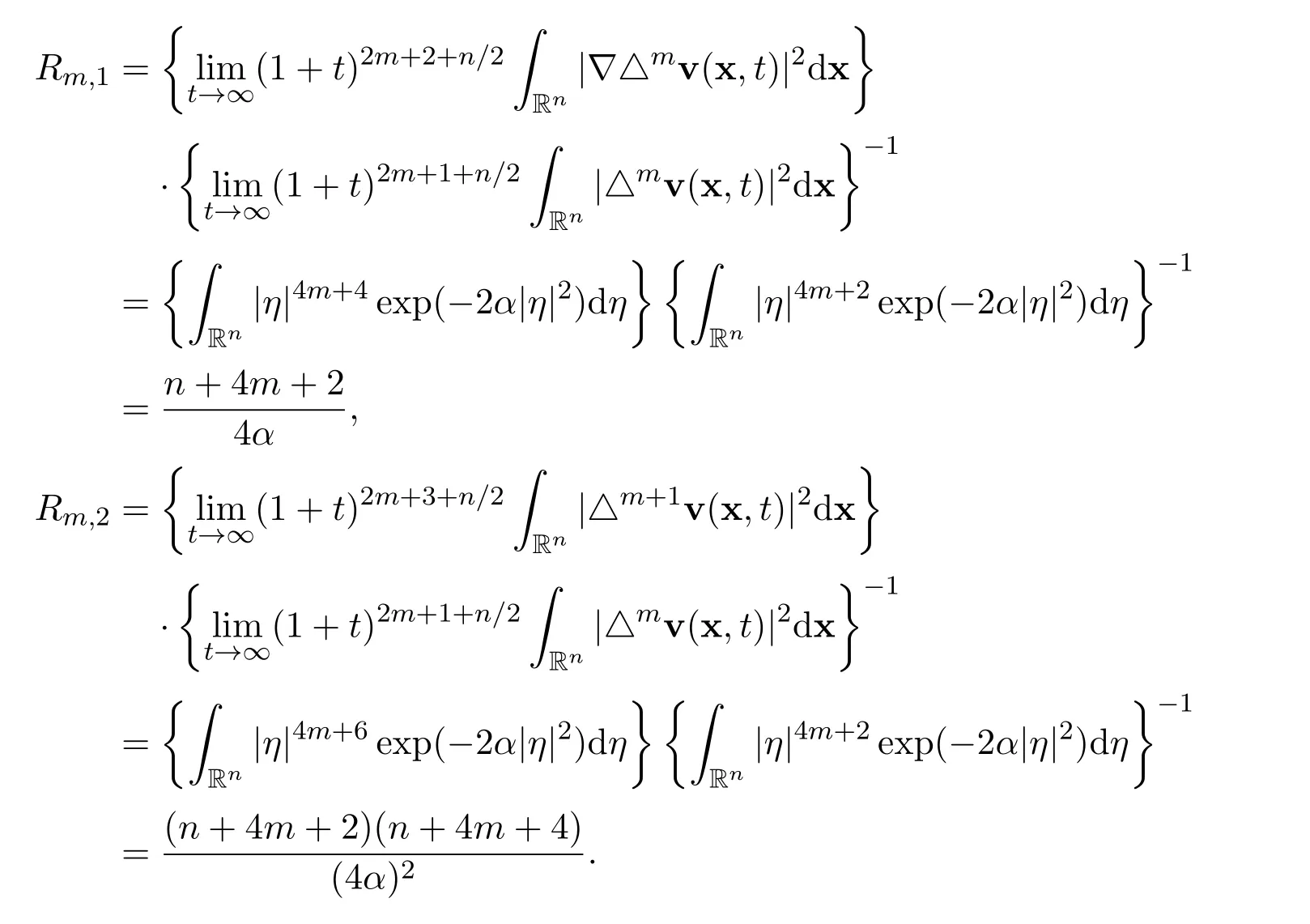
Remark 8For the global smooth solution to the Navier-Stokes equations,we also have

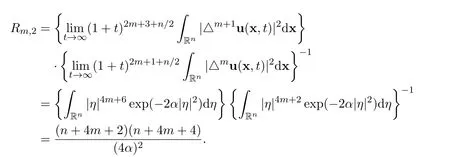
Remark 9Even though we did not find new structures in the Navier-Stokes equations,we did find a very interesting fact. That is,the ratios of the exact limits for both the heat equation and the Navier-Stokes equations are the same,as evidenced by the following computations.Note that the ratios are

and
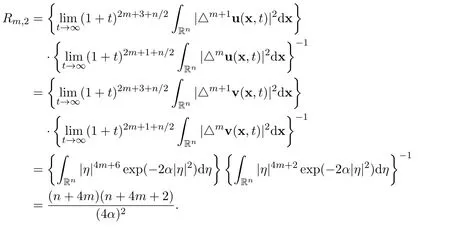
Remark 10For the difference u −v,we have the same ratios as well
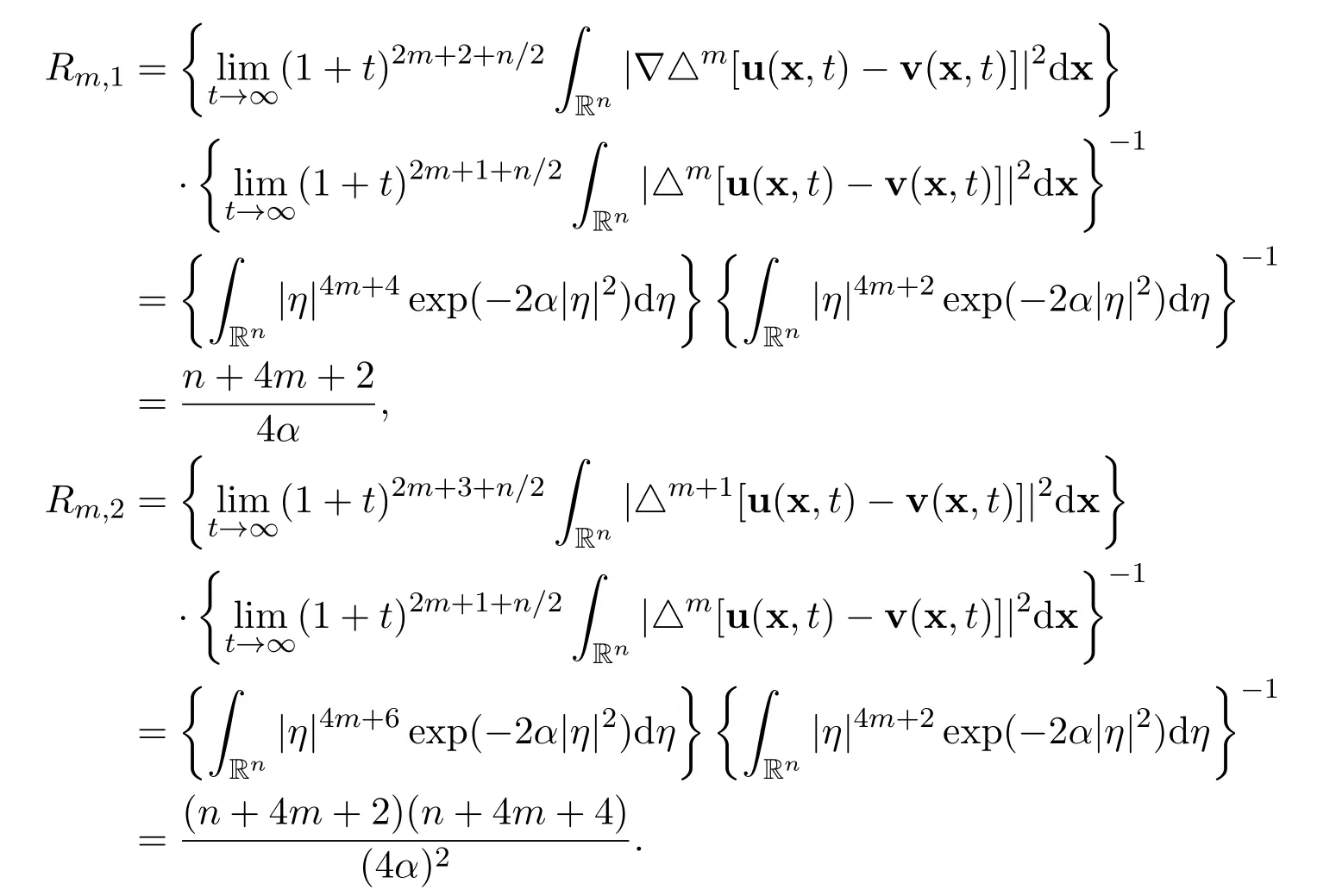
Remark 11The existence of the integrals
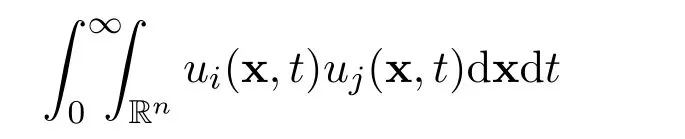
is not a problem,for all i=1,2,3,···,n and j=1,2,3,···,n,because there holds the following decay estimate with sharp rate
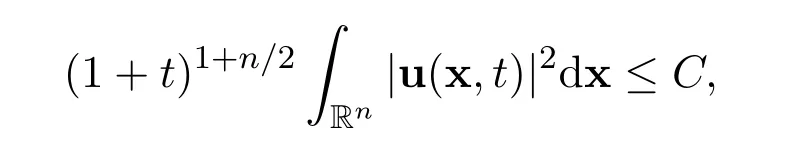
for all t>0,where C>0 is a positive constant,independent of u and(x,t).
Remark 12The exact limits are not completely explicit,because we cannot express the integral
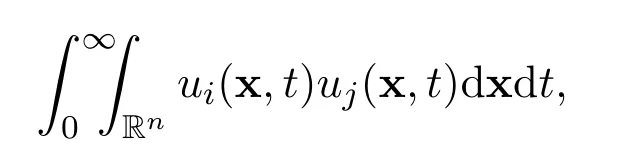
in terms of the integrals

However,based on the results of Theorems 2 and 4,roughly speaking,we have
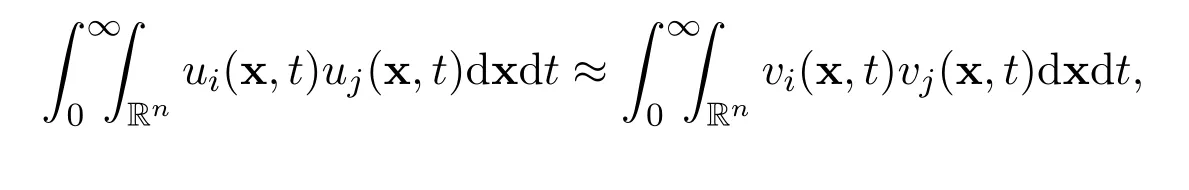
for all i=1,2,3,···,n and j=1,2,3,···,n,where v=v(x,t)represents the global smooth solution to the linear heat equation. Similarly,we may use the following approximation

for all i=1,2,3,···,n and j=1,2,3,···,n.
Remark 13These exact limits are rigorously correct,no matter how many global weak solutions there exist and how many times singularity occur during any finite time interval(T1,T2),where 0 Remark 14A very interesting point is that the exact limits of any order derivatives of the global smooth solution depend only on the integrals for all i=1,2,3,···,n and j=1,2,3,···,n. The exact limits do not depend on the integrals of the derivatives of these functions. Remark 15Numerical simulations for nonlinear equations in higher dimensional spaces,with small diffusion coefficient,have always been a challenging problem.The exact limits may be used to indirectly check the accuracy and stability of numerical schemes for the Navier-Stokes equations. Remark 16We have reasons and strong evidences to believe that for similar equations,very similar results hold. Note that the initial function and the external force are divergence free.Upon performing the Fourier transformation to the equations ∇·u0=0 and ∇·f=0,we get Then let ε →0 and δ →0.Now it is easy to see that for all t>0. For the n-dimensional incompressible Navier-Stokes equations,we made the assumptions that there exist real scalar functions ϕijand ψijin Subsection 1.4,such that The conditions ∇·u0=0 and ∇·f=0 are equivalent to the following We provide the following examples for this kind of initial functions and external forces. Example 1Let α>0 be a positive constant.Define the functions ϕij=ϕij(x)in the initial function by Define the initial function Let δii=1 and δij=0 for i ̸j.Therefore, Moreover Additionally,we have Therefore,if we choose the function ω=ω(x)to be the unique solution to the initial value problems for the nonhomogeneous,second order,linear differential equation then we see that the initial function u0(x)is divergence free. In the initial value problems,and x1,x2,x3,···,xn−1are treated as real parameters.Note that the existence and uniqueness of the global smooth solution ω=ω(x)are guaranteed.There exists a positive constant C>0,independent of x,such that there holds the following estimate Example 2Let α>0 be a positive constant and t>0 be a positive parameter.Define the functions ψij=ψij(x,t)in the external force f=f(x,t)by where i=1,2,3,···,n and j=1,2,3,···,n.Define the external force Define δii=1 and δij=0 for ij.Note that Moreover Additionally Therefore,if we choose the function ω=ω(x,t)to be the unique solution to the initial value problems for the nonhomogeneous,second order,linear differential equation then we see that the external force is divergence free.Overall Now the functions ϕij,u0,ψijand f in the above examples satisfy all assumptions made in(A2). This kind of initial functions and external forces form a vector subspace ofandrespectively. Consider the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations Given any large initial functionand given any large external forcethe existence and uniqueness of the global smooth solutionsuch thathave not been accomplished yet,where m ≥1 is a positive integer. How to find the exact values of the integrals in terms of the diffusion coefficient α,the dimension n and the integrals (The Gagliardo-Nirenberg’s interpolation inequality)Let 1 ≤p ≤∞,1 ≤q ≤∞and 1 ≤r ≤∞.Let m ≥1,n ≥1,k ≥0 be integers,such that k There exists a positive constant C=C(m,n,k,p,q,r)>0,such that there holds the following estimate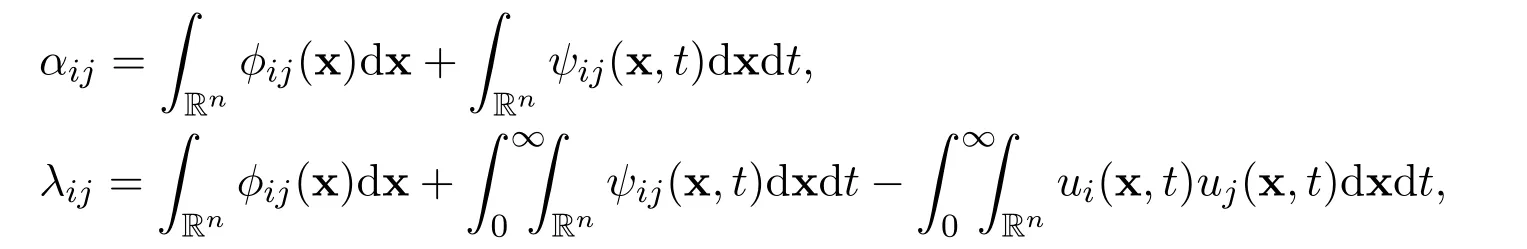
3.3 Examples of initial function and external force for the n-dimensional incompressible Navier-Stokes equations

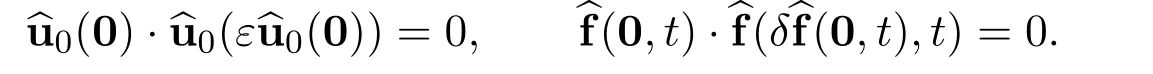


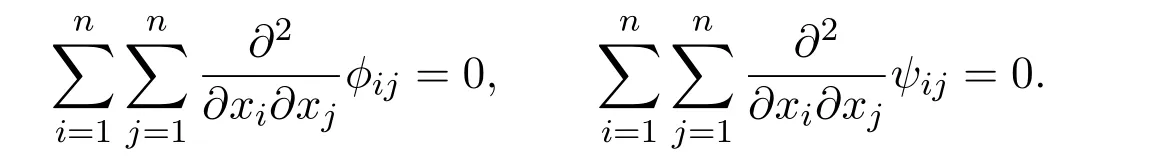


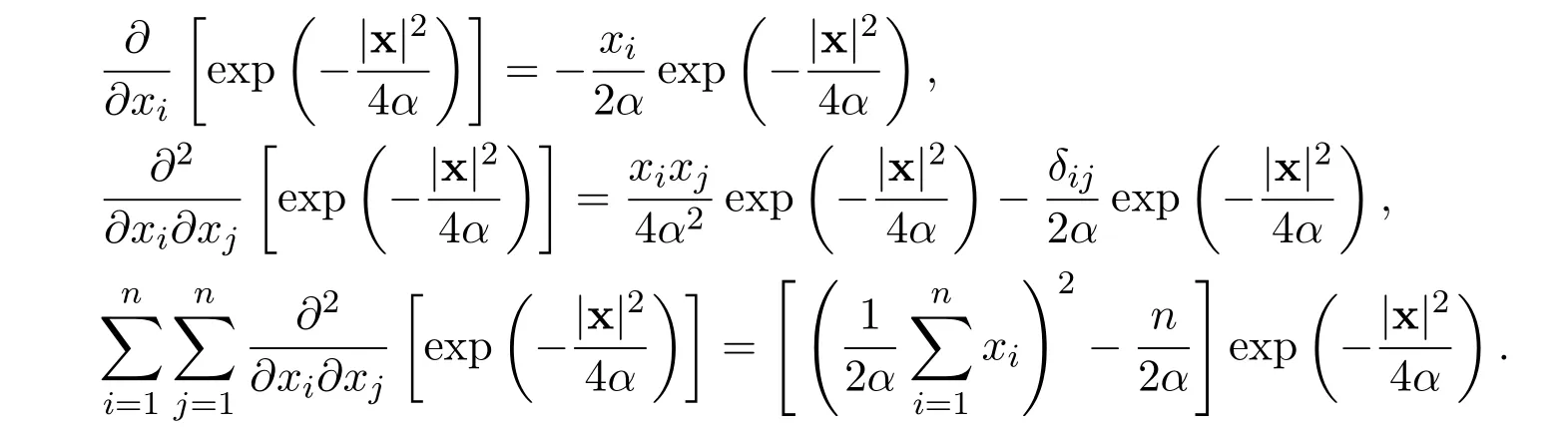
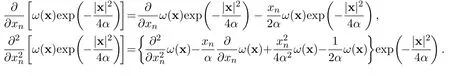
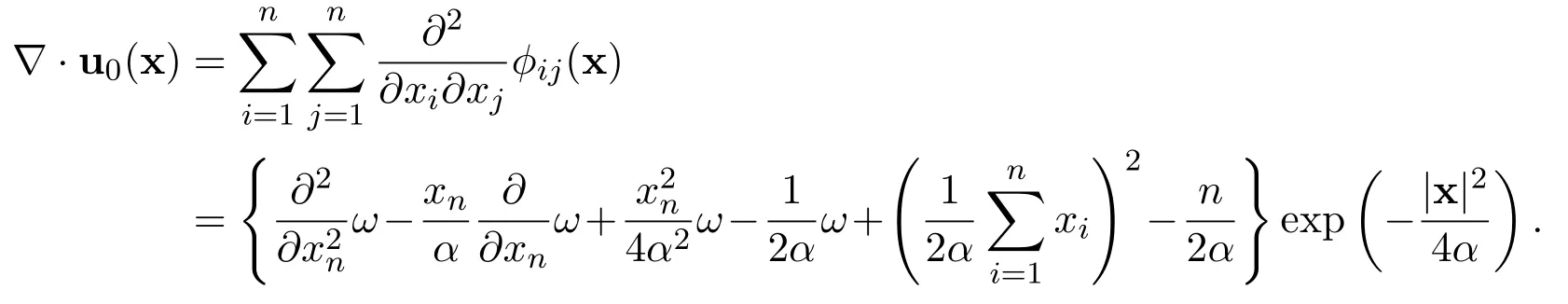
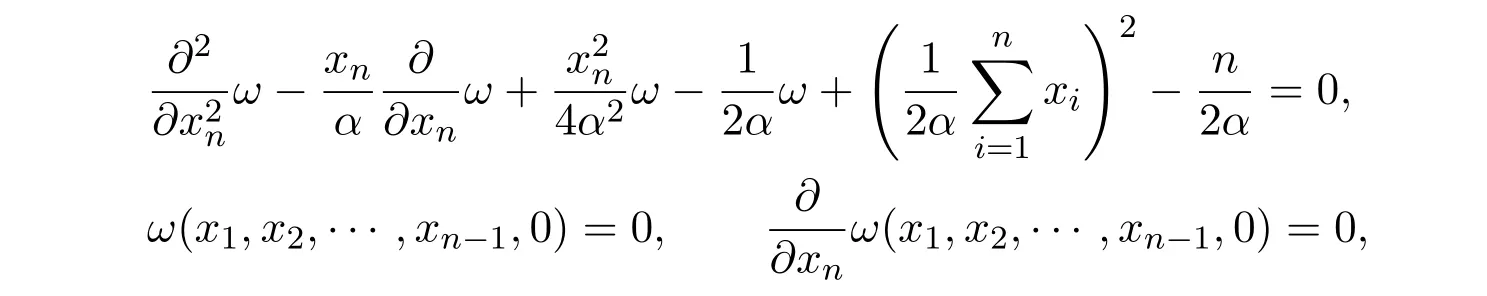
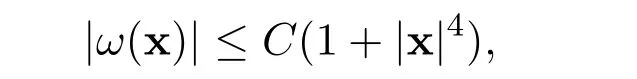
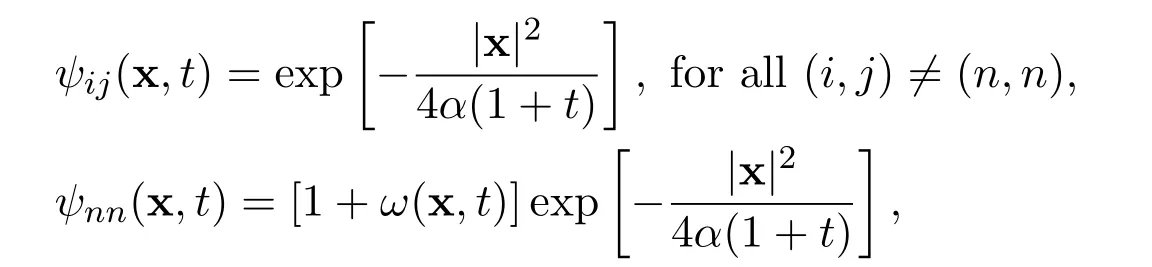
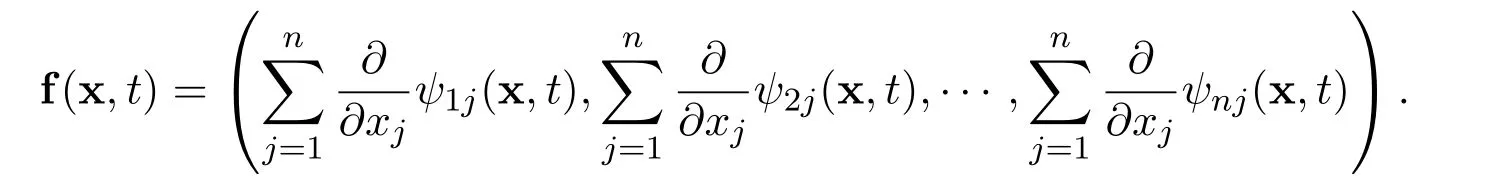
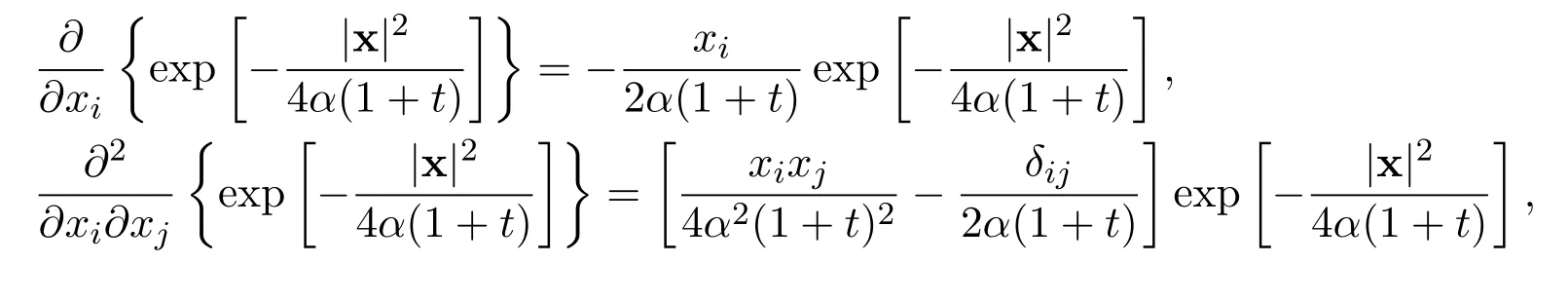
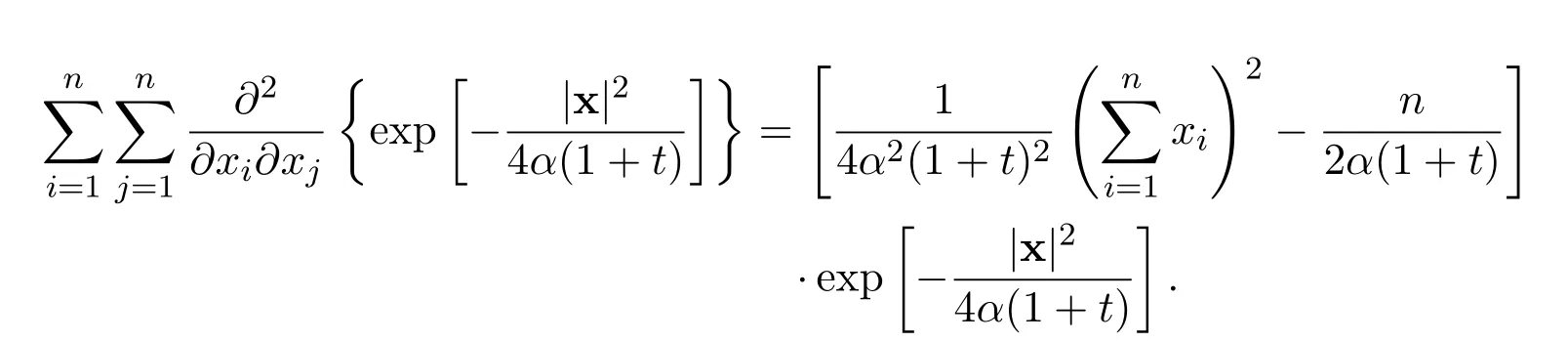
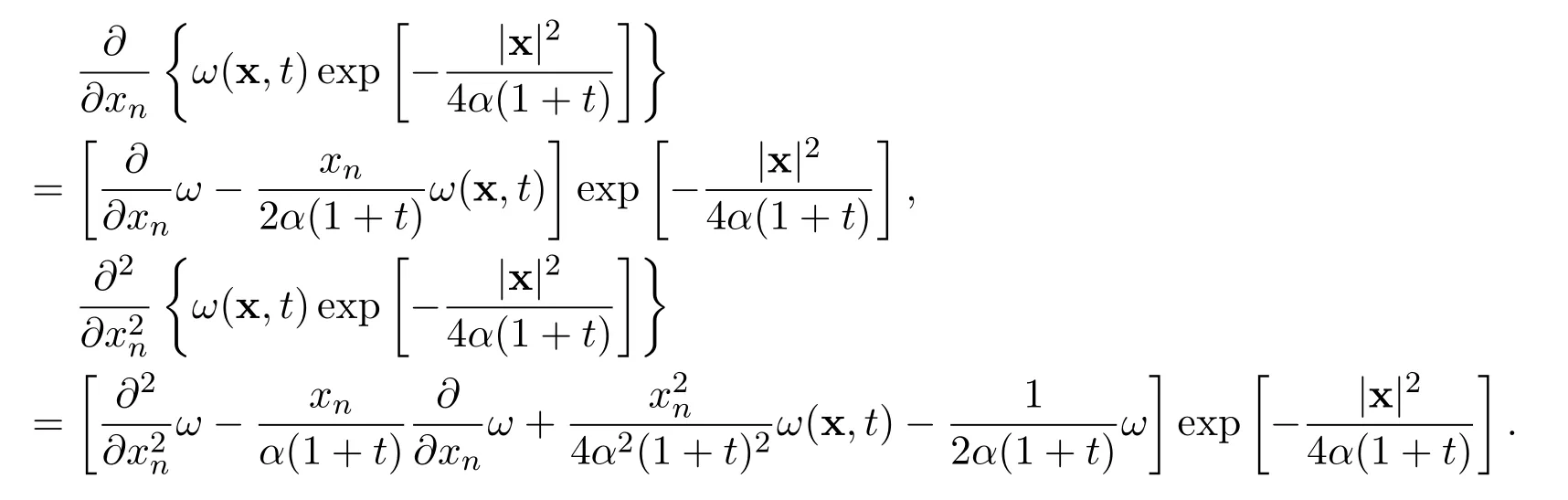
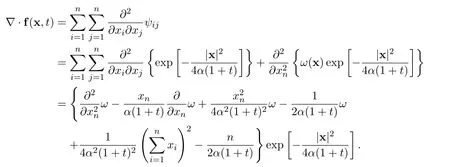


3.4 Open problems
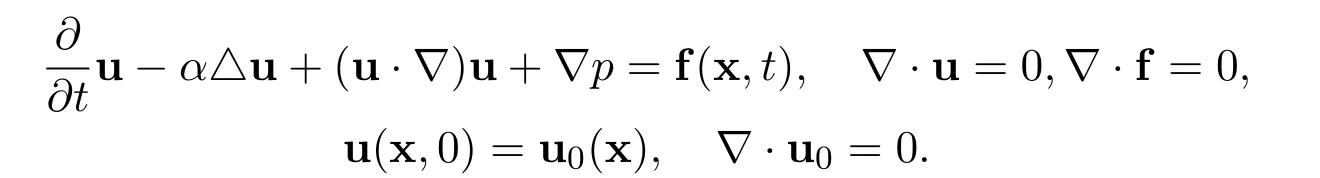
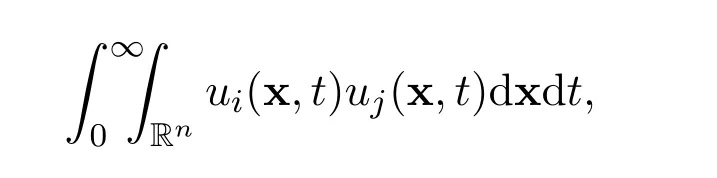
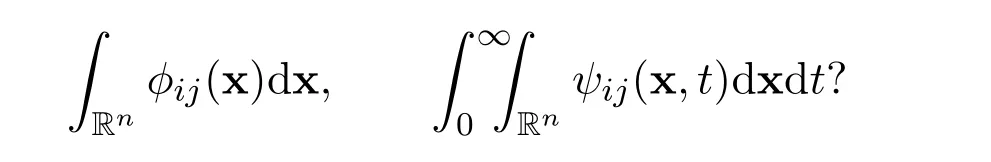
3.5 Some technical lemmas
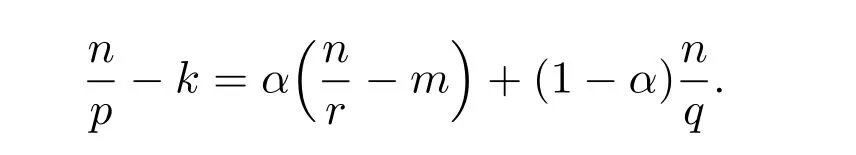
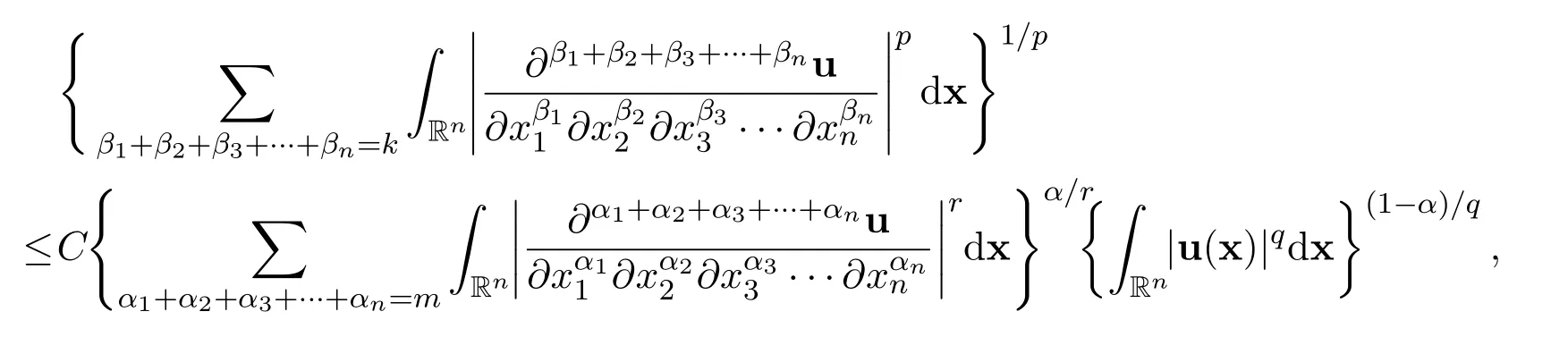
 Annals of Applied Mathematics2019年4期
Annals of Applied Mathematics2019年4期
