MULTIPLE POSITIVE SOLUTIONS FOR A CLASS OF INTEGRAL BOUNDARY VALUE PROBLEM∗†
Yang Yang, Yunrui Yang, Kepan Liu
(School of Math.and Physics,Lanzhou Jiaotong University,Lanzhou 730070,Gansu,PR China)
Abstract In this paper,the existence and multiplicity of positive solutions for a class of non-resonant fourth-order integral boundary value problem
Keywords positive solutions;fixed point;integral boundary conditions
1 Introduction
By the fact of wide applications in a number of scientific fields of boundary value problems for ordinary differential equations,much attention and discussion has been attracted to many scholars[1–5].Especially,an increasing interest in the existence and multiplicity of positive solutions to boundary value problems with integral boundary conditions has been evolved recent years,which arises in the fields of thermo-elasticity,heat conduction,plasma physics and underground water.Moreover,this kind of nonlocal boundary value problems include two-point and multipoint cases[3–6]. For more details about boundary value problems with integral boundary conditions,one can refer to[6–9].
In 2011,Ma[8]considered the existence of positive solutions for the following boundary value problem
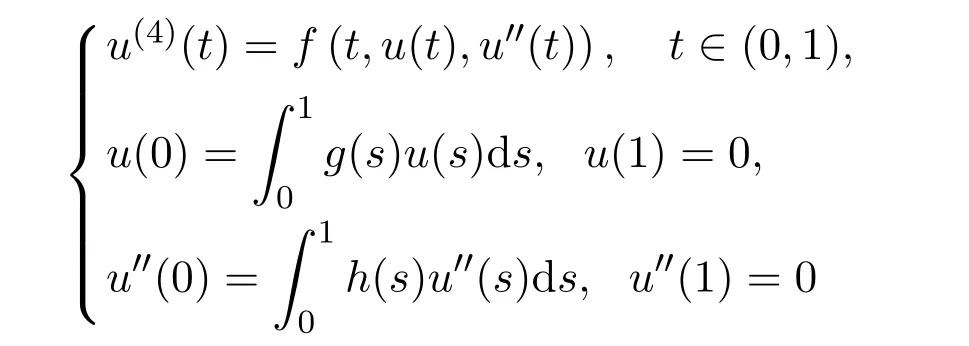
with integral boundary conditions by using the Krein-Rutman theorem and the global bifurcation techniques,where f ∈C([0,1]×[0,+∞)×(−∞,0],[0,+∞))and g,h ∈L1[0,1]are nonnegative.At the same year,by using the operator spectrum theorem together with the fixed point theorem on cone,Chai[9]established some results on the existence of positive solution for the following integral boundary value problem
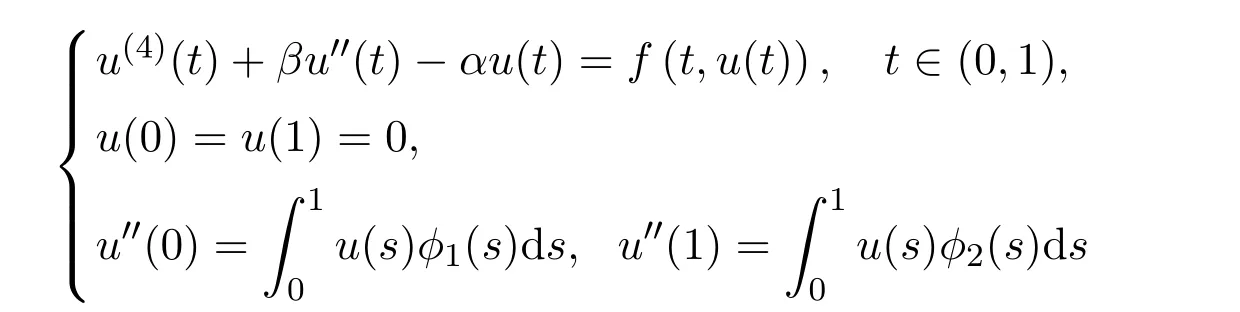
with two parameters,where f ∈C([0,1]×[0,+∞),(−∞,+∞))is allowed to change sign and α,β ∈R,β<2π2,α ≥−β2/4,α/π4+β/π2<1,ϕ1,ϕ2∈C([0,1],(−∞,0]).
The above results mentioned are mainly dealt with the existence of positive solutions.However,there are not few results on the existence of multiple positive solutions for integral boundary value problems.For completeness,the main purpose of this paper is to investigate the multiplicity of positive solutions for the following non-resonant fourth-order integral boundary value problem

with two parameters.
Throughout this paper,we make the following assumptions:
(H1)α,β ∈R,β<2π2,α>0,α/π4+β/π2<1;
(H2)λ1,λ2are the two roots of the polynomial P(λ)=λ2+βλ −α and λ1,2=
(H3)f ∈C([0,1]×[0,+∞)×(−∞,0],[0,+∞))and f(t,u,v)>0,for any t ∈and|u|+|v|>0;q(t)∈L1[0,1]are nonnegative satisfying that there exists a number M>0 such that

The assumption(H1)implies an nonresonance condition by the fact that α>0 ≥−β2/4.By(H1)and(H2),it is not difficult to check that −π2<λ1<0<λ2.
2 Preliminaries
In this section,we first state some definitions and preliminary results which will be applied to prove the main results in this paper.
Denote
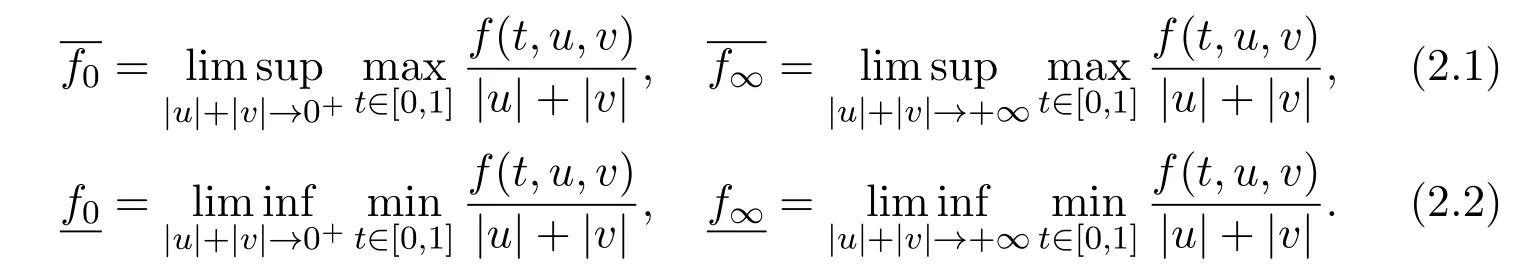
Let Gi(t,s)(i=1,2)be the Green’s function of the following boundary value problem
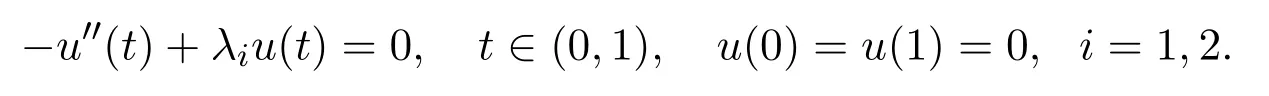
From[5],Gi(t,s)(i=1,2)is given by
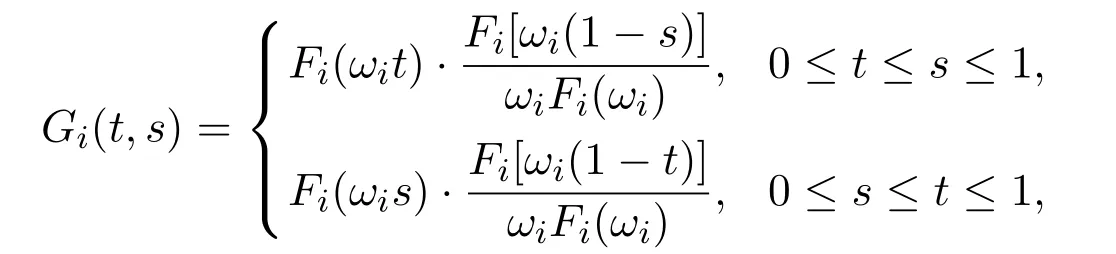
where F1(t)=sin t,F2(t)=sinh t,(i=1,2)and ω2>0,0<ω1<π by the fact that −π2<λ1<0<λ2.
Lemma 2.1[5]Gi(t,s)(i=1,2)has the following properties:
(i)Gi(t,s)>0,for any t,s ∈(0,1).
(ii)Gi(t,s)≤CiGi(s,s),for any t,s ∈[0,1],where Ci>0 is a constant,and C1=1/sin ω1,C2=1.
(iii)Gi(t,s)≥δiGi(t,t)·Gi(s,s),for any t,s ∈[0,1],where δi>0 is a constant,and δ1=ω1sin ω1,δ2=ω2/sinh ω2.
Theorem 2.1[10](Guo-Krasnoselskii’s fixed-point theorem) Let E be a Banach space,K ⊂E be a cone in E.Assume that Ω1and Ω2are bounded open subsets of
E with 0 ∈Ω1and,andis a completely continuous operator such that either
(i)∥Tu∥≥∥u∥,u ∈K ∩∂Ω1and ∥Tu∥≤∥u∥,u ∈K ∩∂Ω2;or
(ii)∥Tu∥≤∥u∥,u ∈K ∩∂Ω1and ∥Tu∥≥∥u∥,u ∈K ∩∂Ω2holds,then T has a fixed point in
Let C[0,1]be equipped with the maximum normand C2[0,1]be equipped with the norm ∥u∥2=∥u∥+∥u′′∥=Denote
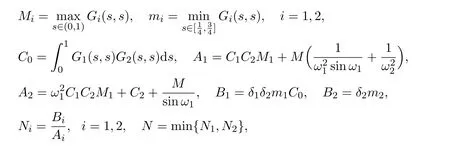
and they are all positive.Define a cone K in C2[0,1]by
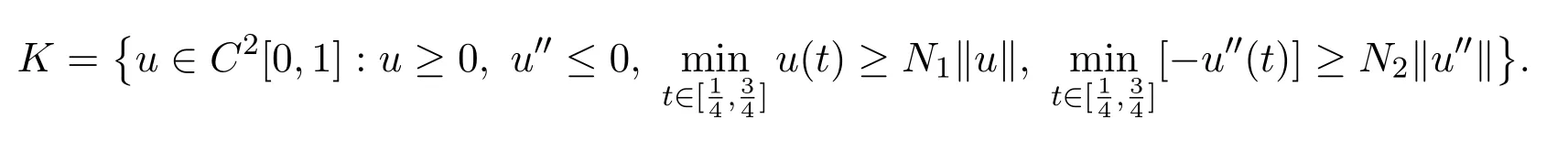
Define an integral operator A:K →C2[0,1]by
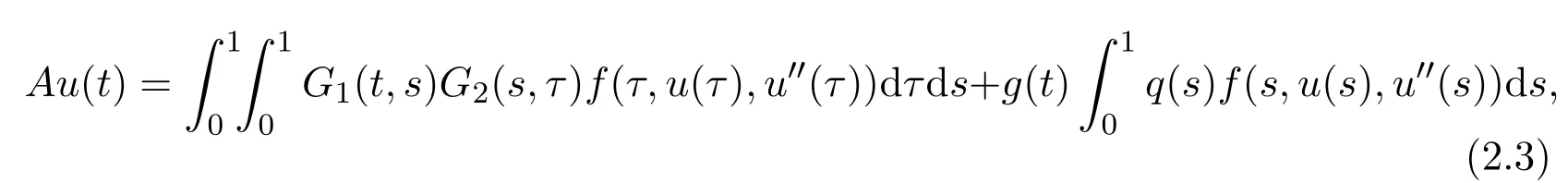
Lemma 2.2Assume that(H1)-(H3)hold.Then u(t)is a solution for the BVP(1.1)if and only if u(t)is a fixed point of the integral operator A.
Lemma 2.3Assume that(H1)-(H3)hold. Then A:K →K is completely continuous.
ProofBy the definition of g(t)and ω2>0,0<ω1<π,it is easy to verify that g(t)≥0 for any t ∈[0,1].Combining g(t)≥0,(i)of Lemma 2.1,(H3)and(2.3),we obtain Au(t)≥0.
Next,from(2.3),for any u(t)∈K and t ∈[0,1],it follows that
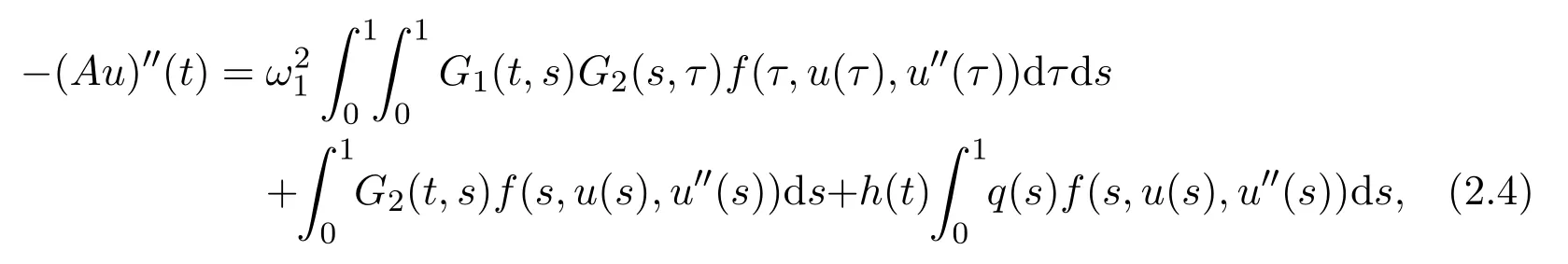
where h(t)=sin ω1t/sin ω1−sinh ω2t/sinh ω2,and thus h(0)=h(1)=0,h′′(t)≤0 for t ∈[0,1],which implies h(t)≥0 for t ∈[0,1].Therefore,we can conclude that(Au)′′(t)≤0.
By(2.3),(H3)and(ii)of Lemma 2.1,for any u(t)∈K and t ∈[0,1],it follows that
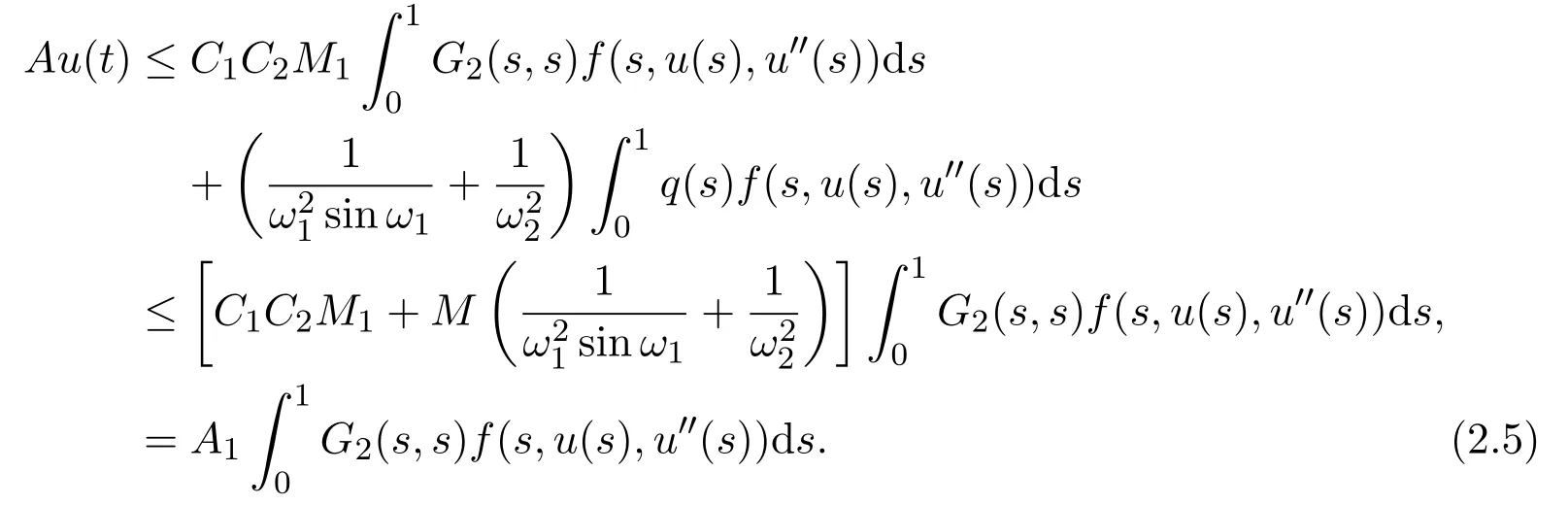
By(2.3),(2.5)and(iii)of Lemma 2.1,for any u(t)∈K andwe have

Similarly,by(2.4),(H3)and(ii),(iii)of Lemma 2.1,for any u(t)∈K,we get
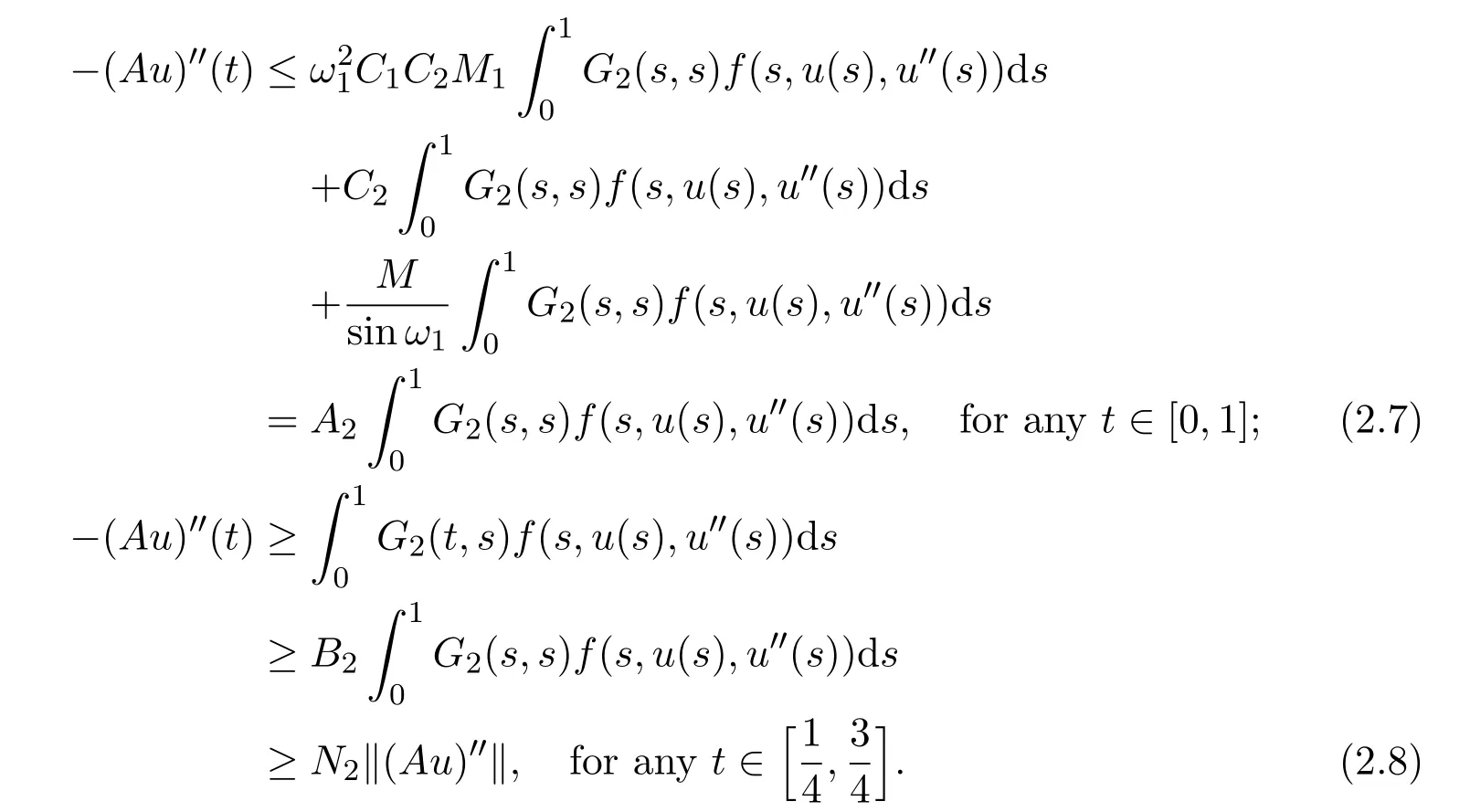
Furthermore,by Arzela-Ascoli theorem,the operator A is completely continuous.This completes the proof.
Corollary 2.1|u(t)|+|u′′(t)|≥N∥u∥2,for any u(t)∈K and t ∈
Lemma 2.4Suppose that(H1)-(H3)hold,then for the operator A and any u ∈K,the following conclusions hold:
ProofIn view of the proofs of(ii)and(iii)are similar to those of(i)and(iv)respectively,here we give only the proofs of(i)and(iv).
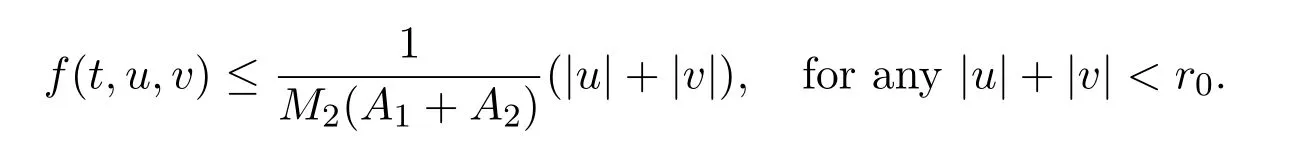
Letting 0 From(2.5)and(2.7),we obtain Therefore,∥Au∥2=∥Au∥+∥(Au)′′∥≤r=∥u∥2. Letting R ≫R0/N,by Corollary 2.1,we get and u ∈K with ∥u∥2=R.Therefore, From(2.8),we have for any t ∈[0,1]and u ∈K with ∥u∥2=R.This completes the proof. In this section,we state and prove the main results of this paper on the existence and multiplicity of positive solutions for(1.1). Theorem 3.1Suppose(H1)-(H3)hold.If either ProofLet E=C2[0,1],Ω1={u ∈E:∥u∥2 Suppose(i)holds. Then,according to Lemma 2.4,we can get ∥Au∥2≤∥u∥2for any u ∈E with ∥u∥2=r,and ∥Au∥2≥∥u∥2for any u ∈E with ∥u∥2=R,respectively,which imply that Theorem 2.1 holds.Therefore,it immediately follows that A has a fixed point Similarly,under the condition(ii),it also follows that A has a fixed point u0(t)∈from Lemma 2.4 and Theorem 2.1.Moreover,by(2.6)and(H3),we have Thus,by Lemma 2.2,u0is also the positive solution for the BVP(1.1).The proof is completed. Corollary 3.1Suppose(H1)-(H3)hold.If either holds,then the BVP(1.1)has at least one positive solution. Example 3.1Consider the following boundary value problem where q(t)=G2(t,t),M=1,f(t,u,v)=α=2π2and β=π.Then,by some calculations,we get which implies(i)of Theorem 3.1 holds.Therefore,by Theorem 3.1,the BVP(3.1)has at least one positive solution. Theorem 3.2Suppose(H1)-(H3)hold.If one of the following two conditions holds: ProofSince the proof of(ii)is similar to that of(i),here we only give the proof of(i). Let E=C2[0,1], Ω1={u ∈E:∥u∥2 Therefore,∥Au∥2≥∥u∥2for any u ∈K ∩∂Ω3. Applying Theorem 2.1,the BVP(1.1)has two positive solutions u1(t)∈K ∩Together with Theorem 3.1,it follows that the BVP(1.1)has two distinct positive solutions u1(t)and u2(t).The proof is completed. Corollary 3.2Suppose(H1)-(H3)hold,and f satisfies either then the BVP(1.1)has at least two positive solutions. Example 3.2Consider the following boundary value problem where q(t)=G2(t,t),M=1,f(t,u,v)=,α=4 and β=3.Then,by some calculations,we obtain which implies(ii)of Theorem 3.2 holds.Therefore,by Theorem 3.2,the BVP(3.2)has at least two positive solutions.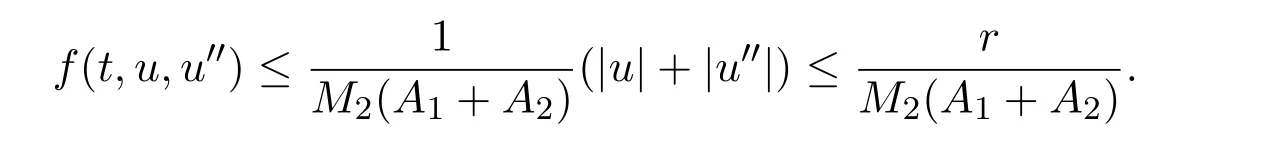
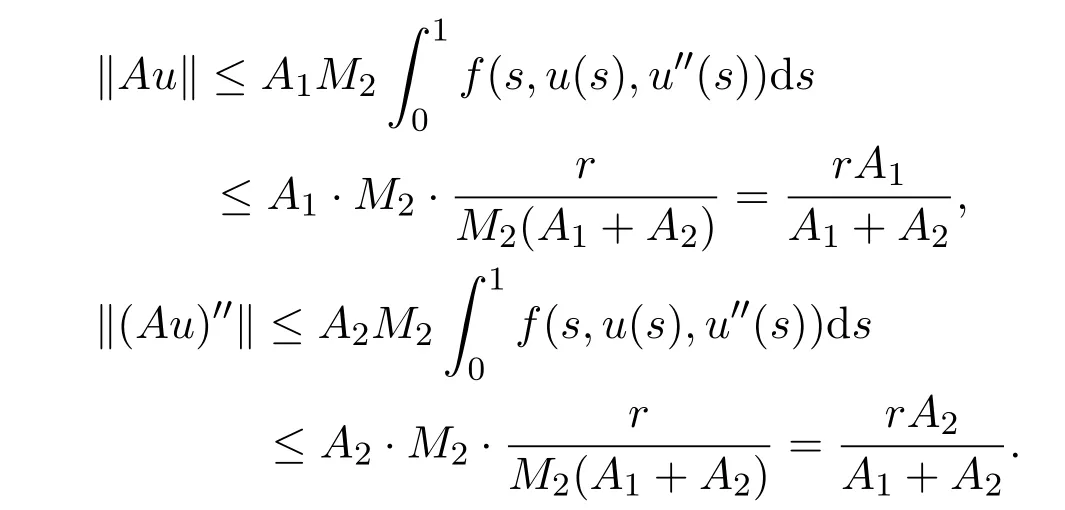
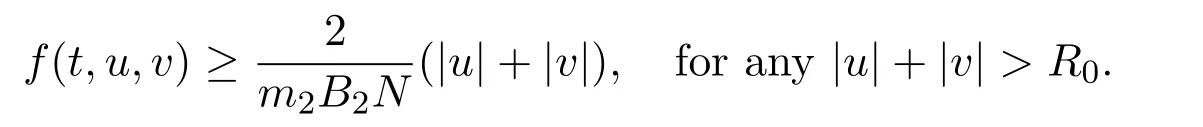

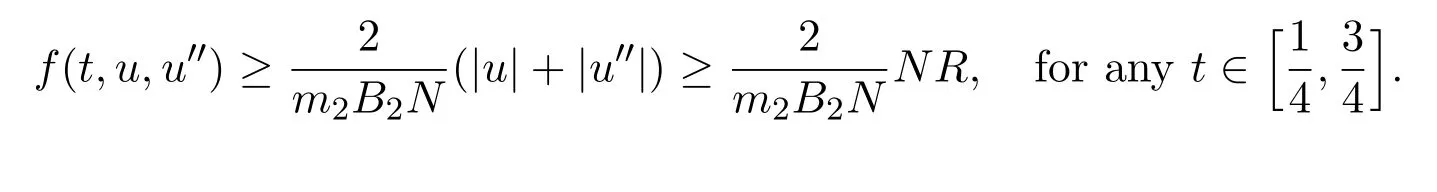
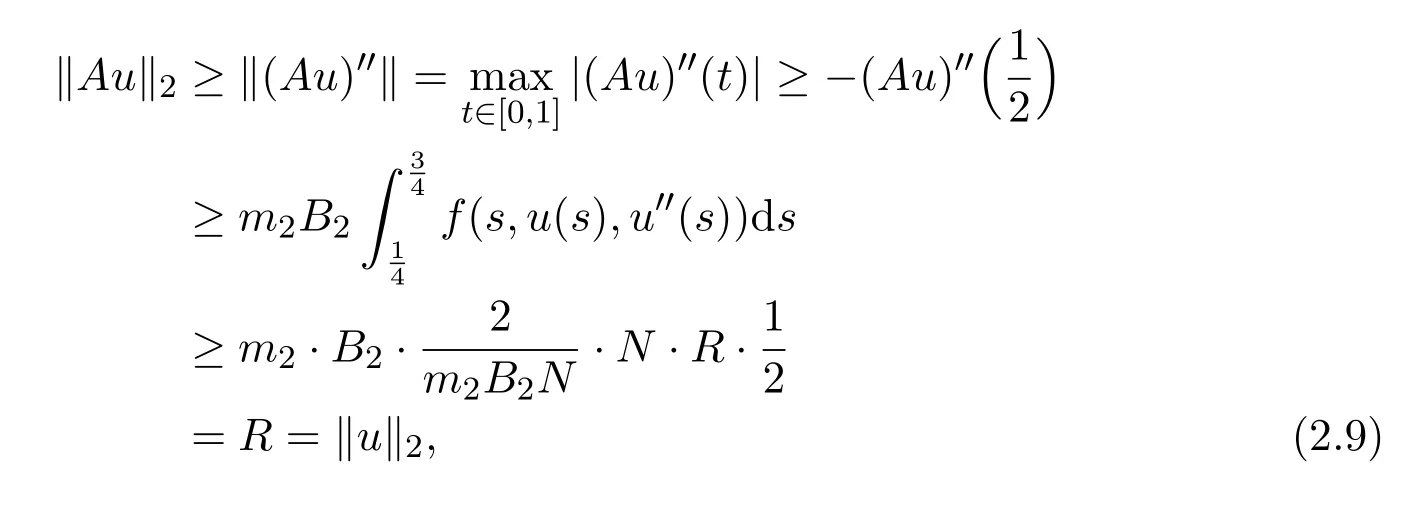
3 Main Results
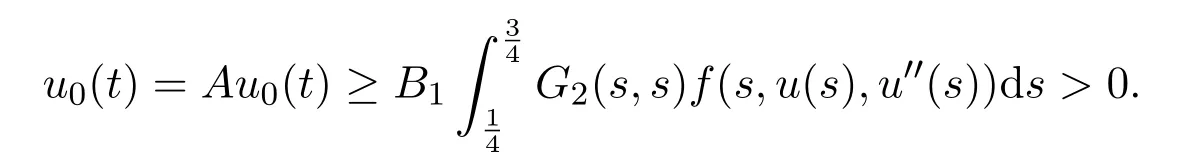


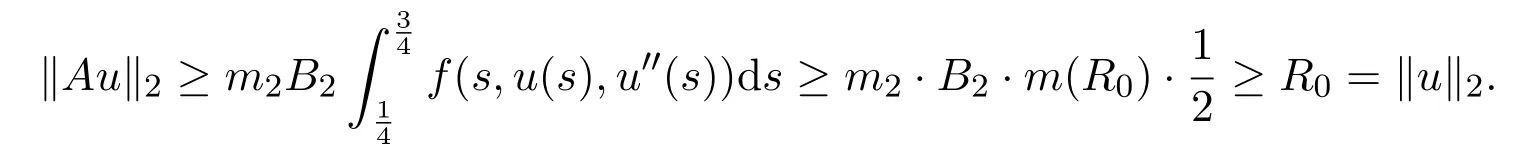
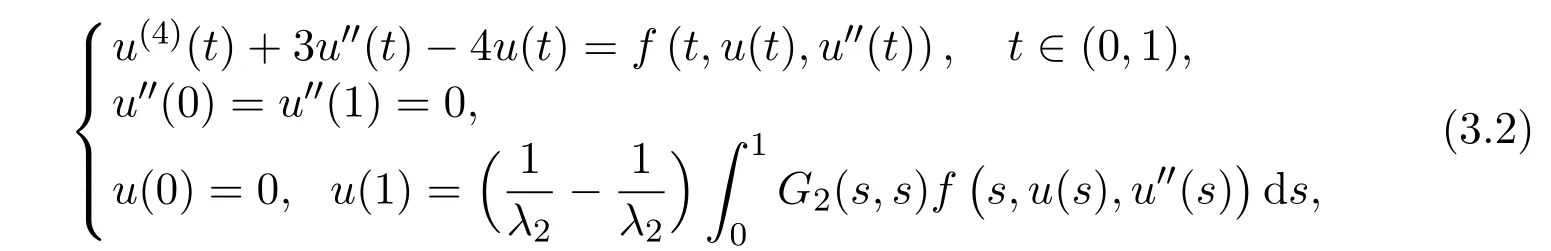
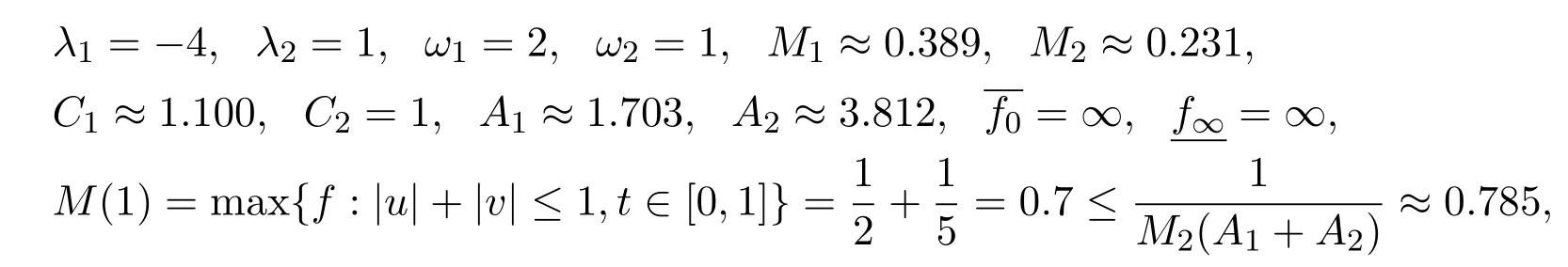
 Annals of Applied Mathematics2019年4期
Annals of Applied Mathematics2019年4期
