SEYMOUR’S SECOND NEIGHBORHOOD IN 3-FREE DIGRAPHS ∗
Bin Chen, An Chang
(Center for Discrete Math.and Theoretical Computer Science,Fuzhou University,Fuzhou 350108,Fujian,PR China)
Abstract
Keywords Seymour’s second neighborhood conjecture;3-free digraph
1 Introduction
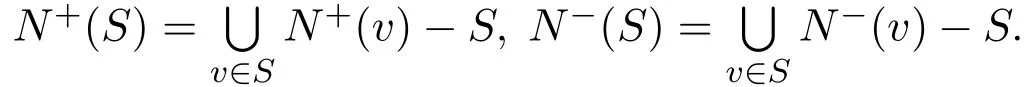
For the purpose of this paper,all cycles considered here are direct cycles.The girth g(D)of D is the minimum length of the cycles of D. A digraph D is k-free means that g(D)≥k+1 for k ≥2,that is,there is no cycle whose length is less than k in D.
In 1990,Seymour[1]put forward the following conjecture:
Conjecture 1.1(Seymour’s Second Neighborhood Conjecture)For any digraph D,there exists a vertex v such that d++(v)≥d+(v).
We call the vertex v in Conjecture 1.1 a Seymour vertex. In 1996,Fisher[3]proved that Conjecture 1.1 is true if D is a tournament.In 2007,Fidler and Yuster[2]showed that any tournament minus a star or a sub-tournament,and any digraph D with minimum degree|V(D)|−2 has a Seymour vertex.In 2016,Cohn et al[8]proved that almost surely there are a large number of Seymour vertices in random tournaments and even more in general random digraphs.However,Conjecture 1.1 is still an open problem for general digraphs.
Another approach to Conjecture 1.1 is to determine the maximum value of λ such that there is a vertex v in D satisfying d++(v)≥λd+(v)for any digraph D.Chen,Shen and Yuster[4]proved that d++(v)≥λd+(v),λ=0.6572···is the unique real root of the equation 2x3+x2−1=0. In 2010,Zhang and Zhou[7]proved that for any 3-free digraph D,there exists a vertex v in D such that d++(v)≥λd+(v),where λ=0.6751···is the only real root in the interval(0,1)of the polynomial x3+3x2−x−1=0.Liang and Xu[6]considered k-free digraphs,k ≥3,and proved that d++(v)≥λkd+(v),where λkis the only real root in the interval(0,1)of the polynomial
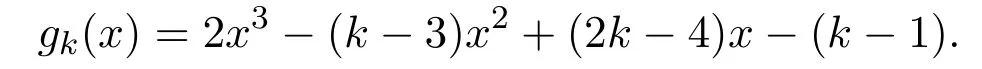
Furthermore,λkis increasing with k,and λk→1 while k →∞.When k=3,λ3=0.6823···is the only real root in the interval(0,1)of the polynomial x3+x−1=0.
In this paper,we consider Seymour’s second neighborhood conjecture in 3-free digraphs,and our result slightly improves the known results in 3-free digraphs with large minimum out-degree.
Theorem 1.1Let D be an n order 3-free digraph,then there exists a vertex v ∈V(D)such that d++(v)≥⌊λd+(v)⌋,where λ=0.6958···is the only real root in the interval(0,1)of the polynomial
This paper is organized as follows. In Section 2,we first introduce some definitions and notations used in the paper,and give some lemmas in order to prove Theorem 1.1.In Section 3,we will prove Theorem 1.1.
2 Preparation
A digraph G is a subdigraph of a digraph D if V(G)⊆V(D),A(G)⊆A(D).For any subdigraph G of D,letandFor a set W ⊆V,we let D[W]denote the subgraph induced by W andSimilarly,we can defineFor any two vertex disjoint vertex sets X and Y,denote A(X,Y)as the arc set between X and Y,every arc(x,y)∈A(X,Y)with x ∈X and y ∈Y.
We need the following lemmas to prove Theorem 1.1.
Lemma 2.1The polynomialis strictly increasing and has a unique real root in the interval(0,1).
ProofSincewe have

f′(x)>0 when x ∈(0,1),which implies f(x)is strictly increasing in(0,1).Since f(0)<0 and f(1)>0,f(x)has a unique real root in the interval(0,1).The proof is completed.
Lemma 2.2If x<⌈y⌉,then x Proof(i)If y is an integer,then (ii)If y is not an integer,denote y=y′+c,here y′is an integer and 0 Lemma 2.3Ifthen x>y,where both x and y are real numbers. ProofIf not,we have x ≤y.It is easy to see thata contradiction.The proof is completed. Lemma 2.4where x is an integer and y is a real number. Proof(i)If y is an integer,then (ii)If y is not an integer,denote y=y′+c,here y′is an integer and 0 Lemma 2.5where both x and y are real numbers. Proof(i)If both x and y are integers,then (ii)If x is an integer and y is not an integer,denote y=y′+c,here y′is an integer and 0 (iii)If x is not an integer and y is an integer,denote x=x′+c,here x′is an integer and 0 (iv)If both x and y are not integers,denote x=x′+c1,y=y′+c2,here both x′and y′are integers and 0 The proof is completed. Lemma 2.6[5]Let D be an n order digraph with δ+(D)≥⌈0.3465n⌉,then D contains a directed triangle. Lemma 2.7Let D be an n order 3-free digraph withand0.3465/2<α<0.3465,then ProofFor any vertex v ∈V(D),denote X=N+(v),Y=N−(v).So|X|=d+(v)and|Y|=d−(v). There exists a vertex say x ∈X,such that Since X,Y and S are pairwise-disjoint sets since D is 3-free,we can acquire that We sum this inequality over all vertex v ∈V(D),then So we obtain that Since 0.3465/2<α<0.3465 and δ+(D)=<αn+1,rearranging the inequality,we obtain The proof is completed. Proof of Theorem 1.1We prove Theorem 1.1 by induction on the number of vertices.It is trivial for n=1,2,3.Assume that Theorem 1.1 holds for all 3-free digraphs with less than n vertices.When|V(D)|=n,assume to the contrary that for any vertex v ∈V(D),d++(v) Let u ∈V(D)be a vertex with minimum out-degree,that is d+(u)=δ+(D).Let R=N+(u),S=N++(u),r=d+(u)and s=d++(u). It is easy to check that Theorem 1.1 holds for all 3-free digraphs with minimum out-degree less than 7,and every vertex with minimum out-degree satisfieswhere λ=0.6958···is the only real root in the interval(0,1)of the polynomial x3+So we can assume that r ≥7.By our assumption,we have the following inequality: Since D is 3-free,D(R)is 3-free.There exists at least one vertex say x ∈R,such thatby Lemma 2.6.We have that<0.3465|R|=0.3465r by Lemma 2.2.So we obtain that Thus which implies that Assume that there exists a vertex t ∈R such thatthenby Lemma 2.6,which implies thata contradiction. Now we suppose that for every vertex t ∈R,Assume thatwhere α<0.3465 by Lemma 2.6,so δ+(D(R))=>By Lemma 2.3,we have αr>(1 −λ)r.On the other hand,α>0.304,otherwise λ ≥0.696,a contradiction. Thus We have that since(1 −λ)r −0.8>0. Thus,the following inequality holds By induction hypothesis,there exists at least one vertex say w ∈R such thatDenoteY =N+(w)−R=N+(w)∩S and d=|Y|.Sincewe have.Thus, since r ≥7 and λ>0.6535. Since d=|Y|<|S|=s<⌊λr⌋<λr,we conclude that That is, That is, where 0.3r Let where 0.3r for all z ∈(0.3r,λr). Combining(6)with(7),we have A simple calculation shows that if λr2>f(0.3r),then λ>0.744,a contradiction.Similarly,if λr2>f(λr),by simplifying there is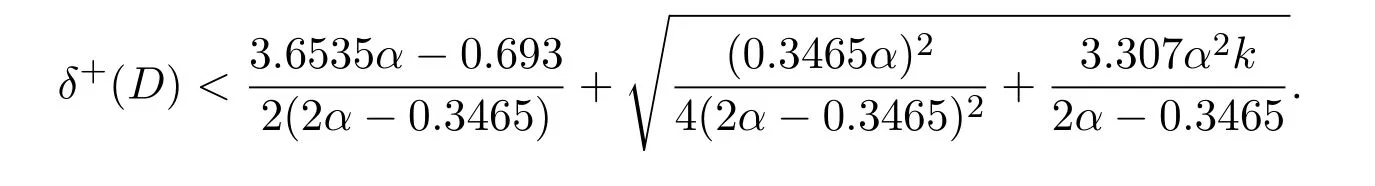
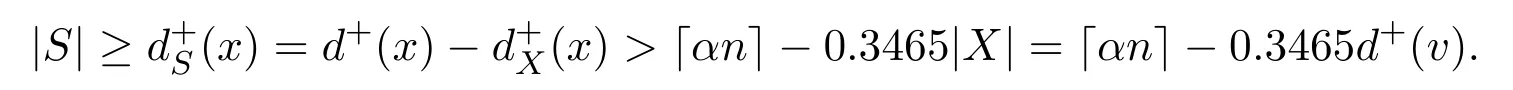

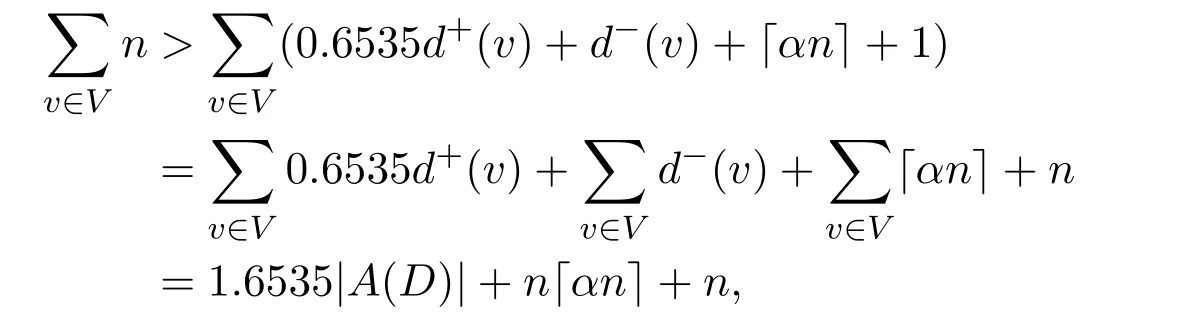
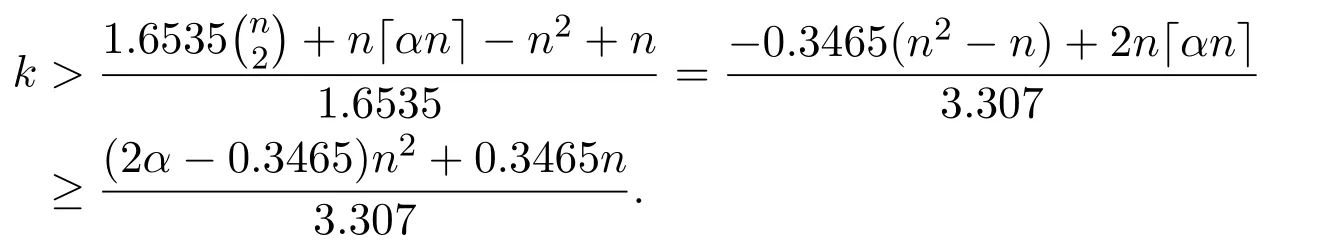
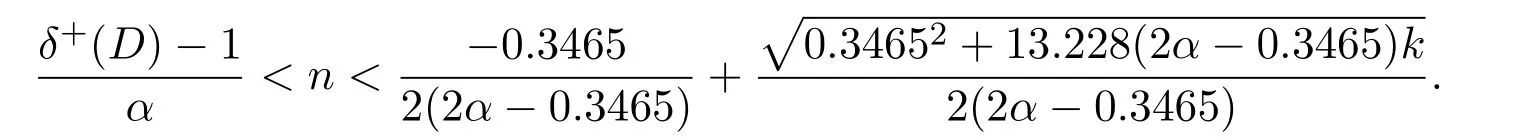
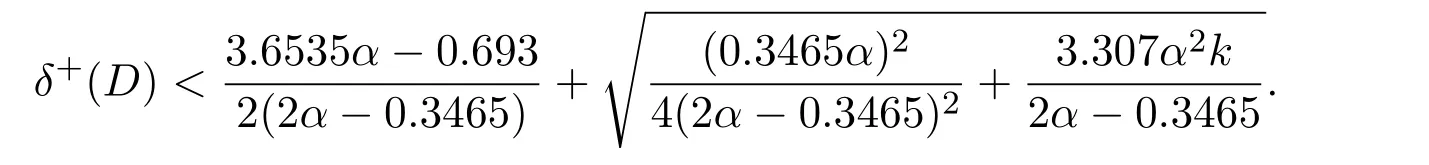
3 Proof of Theorem 1.1


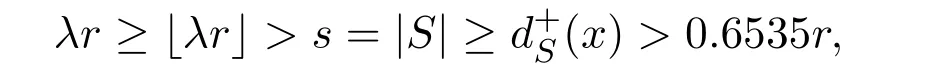

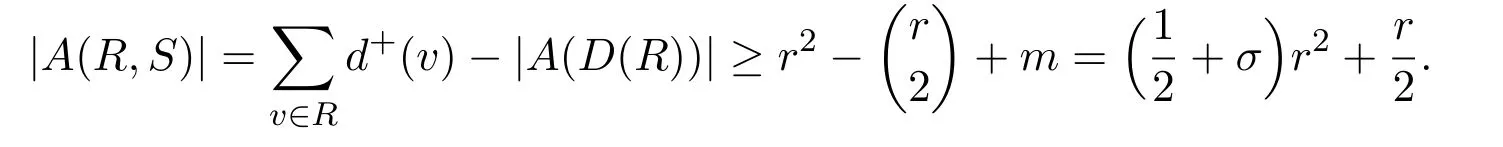

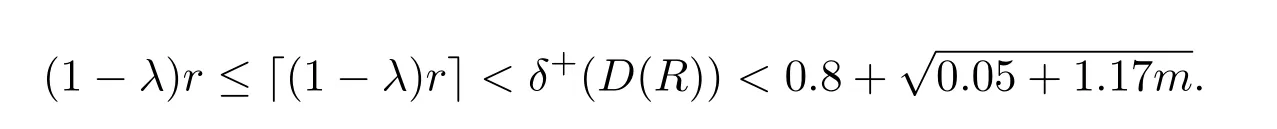
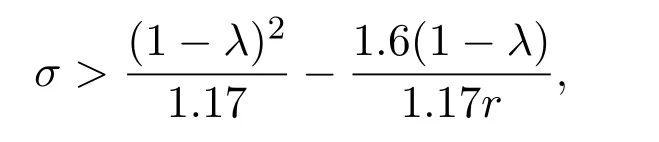



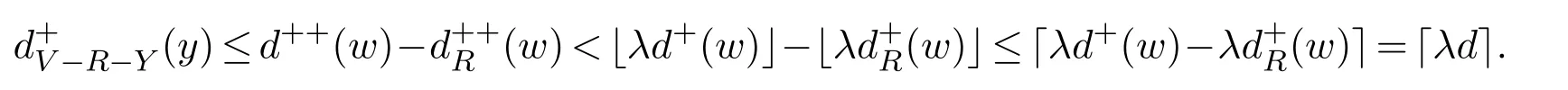
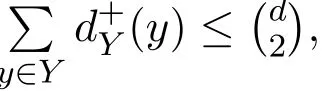
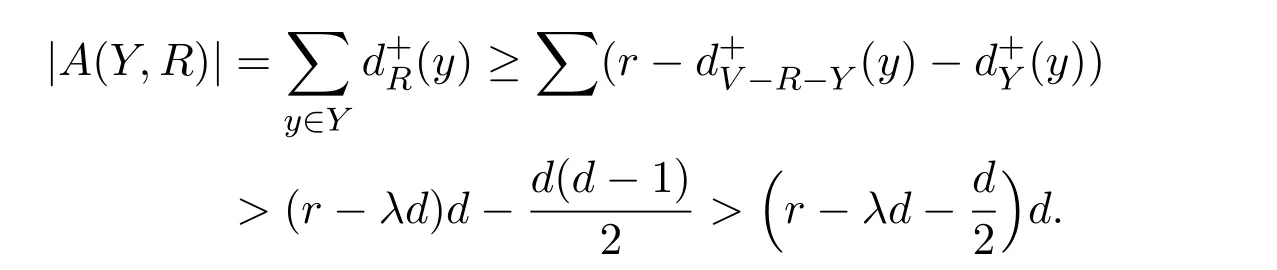
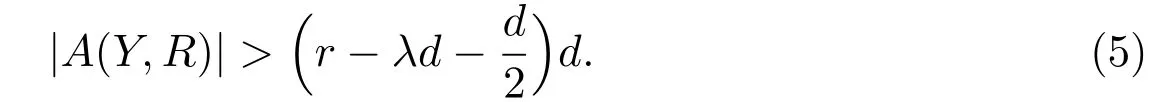


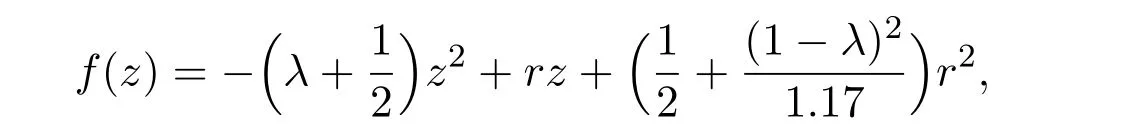
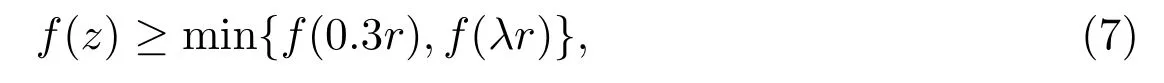
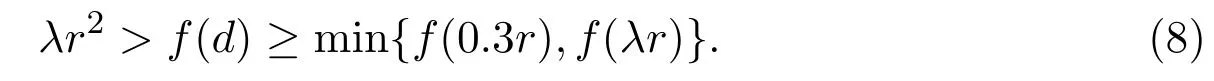

 Annals of Applied Mathematics2019年4期
Annals of Applied Mathematics2019年4期
