DYNAMIC BEHAVIORS OF MAY TYPE COOPERATIVE SYSTEM WITH MICHAELIS-MENTEN TYPE HARVESTING∗†
Xiangqin Yu, Fengde Chen, Liyun Lai
(College of Math.and Computer Science,Fuzhou University,350108 Fuzhou,Fujian,PR China)
Abstract Traditional May type cooperative model incorporating Michaelis-Menten type harvesting is proposed and studied in this paper. Sufficient conditions which ensure the extinction of the first species and the existence of a unique globally attractive positive equilibrium are obtained,respectively. Numeric simulations are carried out to show the feasibility of the main results.
Keywords global attractivity;May type cooperative system;Michaelis-Menten type harvesting;iterative method
1 Introduction
The aim of this paper is to investigate the dynamic behaviors of the following May type cooperative model incorporating Michaelis-Menten type harvesting
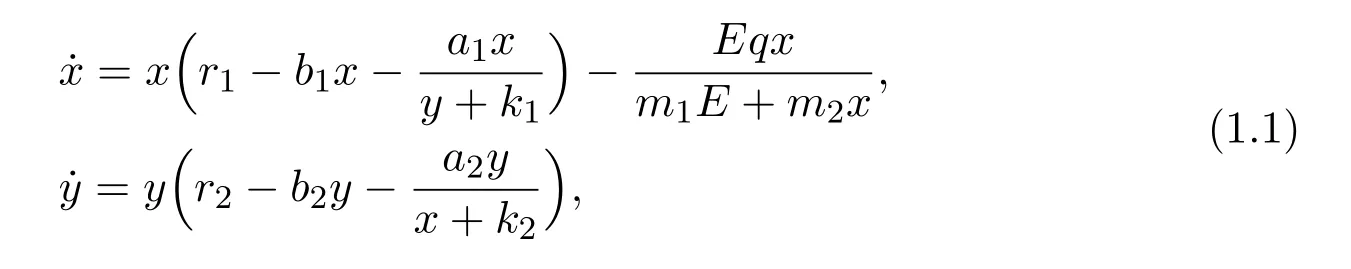
where x and y denote the densities of two populations at time t. The parameters r1,r2,a1,a2,b1,b2,k1,k2,E,q,m1,m2are all positive constants.
During the last decade,many scholars[1-30]investigated the dynamic behaviors of the cooperative system.Yang,Miao,Chen et al[4],Yang and Li[9],Chen,Chen,Li[10],Chen and Xie[11],Han,Xie and Chen[12],Chen and Xie[13],Han,Chen,Xie et al[14],Chen,Yang,Chen et al[15]studied the influence of feedback controls on the cooperative system;May[1],Xie,Chen and Xue[2],Chen,Wu and Xie[3],Xie,Chen,Yang et al[6],Yang,Xie and Chen[7],Chen,Xie and Chen[8],Chen,Xue,Lin et al[16],Wu and Lin[20],Li,Chen,Chen et al[23],Lin[25],Deng and Huang[26],Lei[27,28],Chen[29,30]studied the stability property of the equilibria of cooperative or commensalism model;Chen,Chen and Li[10],Chen and Xie[11],Han,Xie and Chen[12],Chen and Xie[13],Chen,Yang,Chen et al[15],Yang,Xie,Chen et al[19]investigated the persistent property of the cooperative system;Lin[24],Chen[30],Wu[21]investigated the influence of Allee effect on the cooperative system or commensalism system;Xue,Xie and Chen[5],Yang,Xie and Chen[18],Muhammadhaji and Teng[22]investigated the periodic solution or almost periodic solution of the cooperative system.
However,only recently has it attracted the attention of scholars([2,3,25–27,29])to investigate the influence of harvesting on the cooperative or commensalism model.Xie,Chen and Xue[2]studied the following cooperative system incorporating linear harvesting to the first species
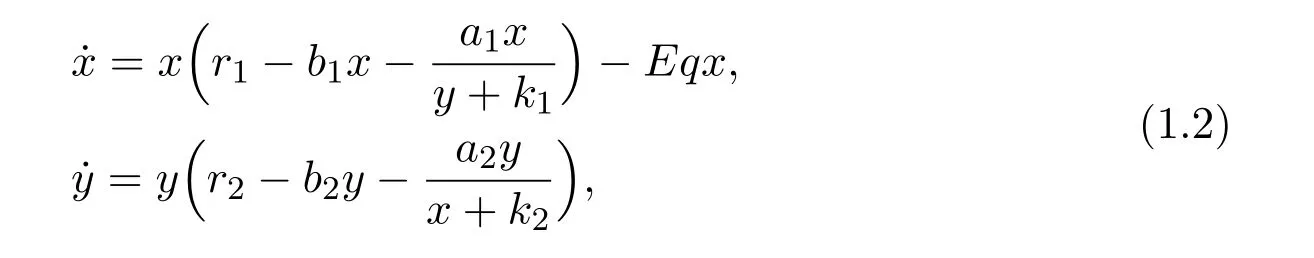
where x and y denote the densities of two populations at time t. The parameters r1,r2,a1,a2,b1,b2,k1,k2,E,q are all positive constants.They showed that if r1>Eq holds,then the unique positive equilibrium E∗(x∗,y∗)of system(1.2)is globally attractive.
Lei[27]studied the dynamic behaviors of the following non-selective harvesting May cooperative system incorporating partial closure for the populations
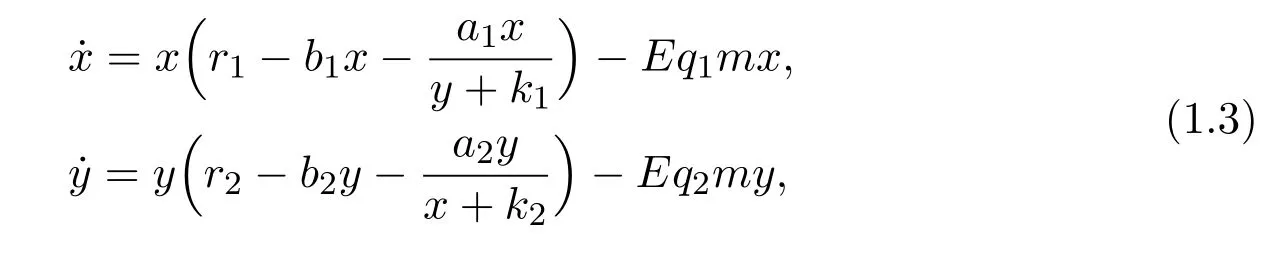
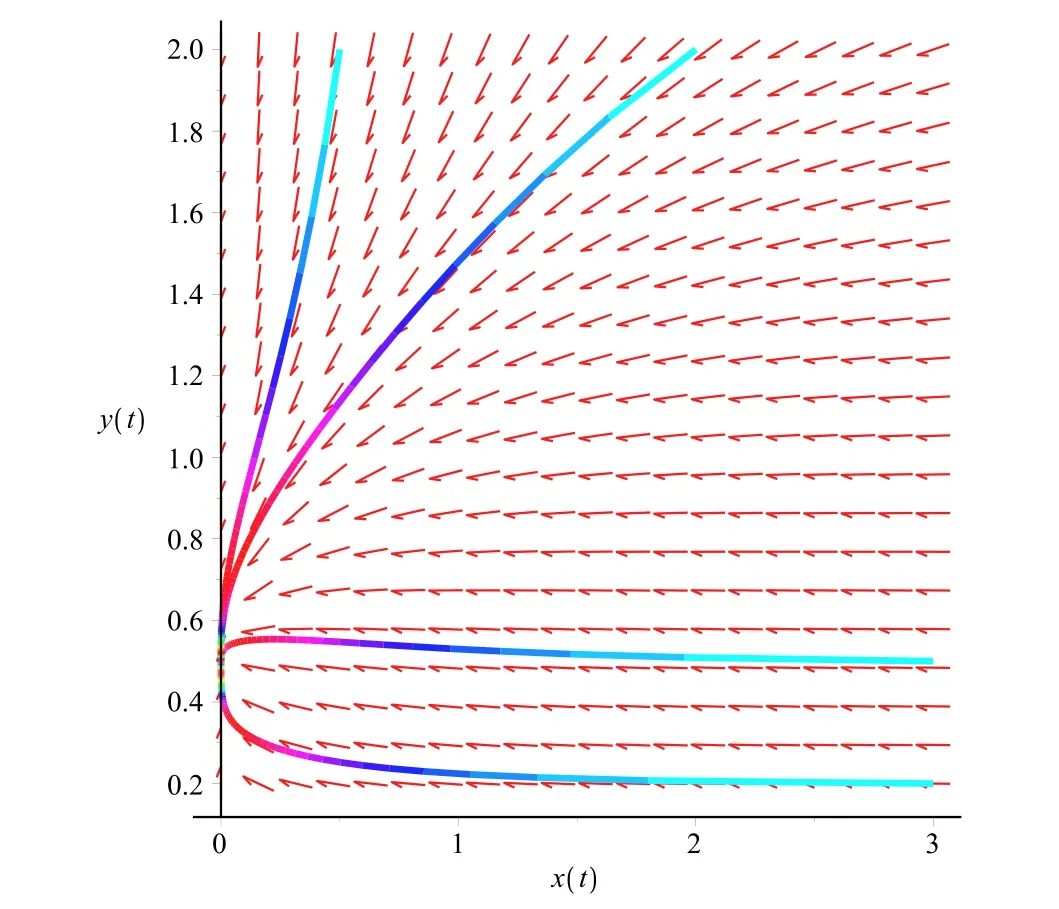
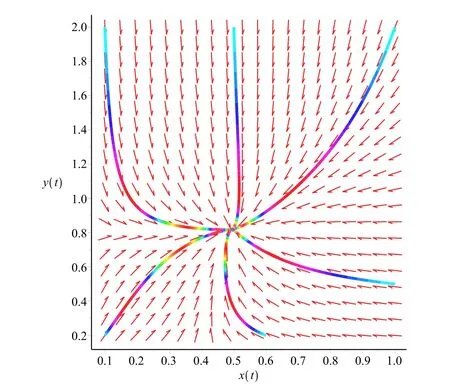
where x and y denote the densities of two populations at time t. The parameters r1,r2,a1,a2,b1,b2,k1,k2,E,q1and q2are all positive constants,E is the combined fishing effort used to harvest and m(0 It brings to our attention that in system(1.2)and(1.3),the authors chose the linear harvesting.Suck kind of harvesting embodies several unrealistic features and limitations. For example,in system(2.1),the authors took h(E,x)=qEx as the fishing term,where E denotes effort.One could see that h tends to infinity as the effort E tends to infinity if the population x is finite and fixed,or as the population x tends to infinity if the effort E is finite and fixed. To overcome this drawback,recently,many scholars[30–33]argued that the nonlinear harvesting,or named as Michaelis-Menten type harvesting is more suitable,it is more appropriate to describe the fishing process of human being. Chen[30]incorporated the Michaelis-Menten type harvesting term to the first species of the commensalism model,and studied the following model: where r1,r2,K1,K2,α,q,E,m1,m2are all positive constants,r1,r2,K1,K2,α have the same meaning as those of system(1.1),E is the fishing effort used to harvest and q is the catchablity coefficient,m1and m2are suitable constants. In system(1.4),where the harvesting term is h(E,x)=qEx/(m1E+m2x),q is the catchability coefficient,E is the external effort devoted to harvesting,one could see thath(E,x)=qx/m1andh(E,x)=qE/m2.Such an assumption obviously overcome the drawback of the linear one. It brings to our attention thatto this day,still no scholars propose and study the cooperative system withe Michaelis-Menten type harvesting.This motivates us to propose system(1.1),that is,we incorporate the Michaelis-Menten type harvesting to the traditional May cooperative system[1]. As far as system(1.1)is concerned,the most important thing is to study the extinction and persistent property of the system. We will investigate the extinction property in the next section,and investigate the stability property of the positive equilibrium in Section 3,finally we end this paper by a briefly discussion. As a direct corollary of Lemma 2.2 of Chen[17],we have: Lemma 2.1If a>0,b>0 and ˙x≥x(b −ax),when t≥0 and x(0)>0,we have If a>0,b>0 and ˙x ≤x(b −ax),when t ≥0 and x(0)>0,we have Concerned with the extinction of the first species,we have the following result. Theorem 2.1Assume that where Then the first species will be driven to extinction,that is, holds,where ProofCondition(2.1)implies that for enough small positive constant ε>0, Now from the second equation of system(1.1),we have Applying Lemma 2.1 to(2.3)leads to Therefore,for ε>0 small enough which satisfies(2.2),there exists a T1>0 such that For t>T1,from(2.5)and the first equation of system(1.1),we have Applying Lemma 2.1 to(2.6)leads to where Hence,there exists a T2>T1such that For t>T2,again,from the first equation of system(1.1),we have Hence, It then immediately follows from(2.2)that This ends the proof of Theorem 2.1. Remark 2.1Condition(2.1)seems a little complicated,since we here try to incorporate the influence of the second species,however,from the proof of Theorem 2.1,in(2.6),from the first equation of system(1.1),we could also have Applying Lemma 2.1 to(2.11),one has From(2.12),with some minor revise of(2.8)-(2.10),we could establish the following more stronger but seems concise result. Corollary 2.1Assume that Then the first species will be driven to extinction,that is, Remark 2.2For the system without fishing,that is,q=0 in system(1.1),May[1]showed that the system admits a unique globally attractive positive equilibrium.That is,two species could be coexist in a stable state.Theorem 2.1 and Corollary 2.1 show the over harvesting of the first species(that is,q in system(1.1)is too large),then despite the cooperation between the species,the first species will still be driven to extinction. Concerned with the stability of the rest species y,we have the following result. Theorem 2.2Assume that(2.1)or(2.13)holds,then ProofIt follows from the second equation of system(1.1)that Applying Lemma 2.1 to(2.15)leads to On the other hand,under assumption(2.1)or(2.13),from Theorem 2.1 and Corollary 2.1,we know that the first species in system(1.1)will be driven to extinction.That is,for any enough small positive constant ε>0,there exists an enough large T such that From(2.17)and the second equation of system(1.1),we have Hence,from Lemma 2.1,we have Since ε is an enough small positive constant,setting ε →0 in(2.19)leads to Combining(2.16)with(2.20),we have This ends the proof of Theorem 2.2. First,let’s investigate the existence of the positive equilibrium of system(1.1). Theorem 3.1Assume that holds,then system(1.1)admits a unique positive equilibrium. ProofThe positive equilibrium of system(1.1)satisfies the equations From the second equation,we have Substituting(3.3)into the first equation of system(3.2)and by simplifying,we finally obtain where Under the assumption of Theorem 3.1,A1>0 and A3<0,hence,(3.4)admits a unique positive solution Consequently,system(1.1)admits a unique positive equilibrium E(x∗,y∗),where x∗is defined by(3.6)and This ends the proof of Theorem 3.1. Remark 3.1Condition b1k2>r1could be replaced by some restrictions but more complex condition where A1is defined by(3.5). Now we are in the position of stating the stability property of the positive equilibrium. Theorem 3.2Assume that(3.1)holds,then system(1.1)admits a unique positive equilibrium E(x∗,y∗),which is globally attractive. ProofBy the first equation of system(1.1),we have From Lemma 2.1,it follows that Hence,for enough small ε>0,without loss of generality,we may assume that It follows from(3.8)that there exists asuch that Similarly,for above ε>0,it follows from the second equation of system(1.1)that there exists asuch that (3.9)and(3.10)together with the first equation of system(1.1)lead to Therefore,by Lemma 2.1,we have That is,for ε>0 which satisfies(3.8),there exists asuch that It follows from(3.9)and the second equation of system(1.1)that Applying Lemma 2.1 to(3.14)leads to Hence,for ε>0 which satisfies(3.8),there exists asuch that Noting that it immediately follows that From the first equation of system(1.1)we have Applying Lemma 2.1 to(3.17)leads to Hence,for ε>0 which satisfies(3.8),there exists asuch that From the second equation of system(1.1),we have Applying Lemma 2.1 to(3.20)leads to Hence,for ε>0 which satisfies(3.8),there exists asuch that (3.19)and(3.22)together with the first equation of system(1.1)imply that Applying Lemma 2.1 to(3.23)leads to That is,for ε>0 which satisfies(3.8),there exists asuch that From the second equation of system(1.1),we have Applying Lemma 2.1 to(3.20)leads to Hence,for ε>0 which satisfies(3.8),there exists asuch that and so Repeating the above procedure,we get four sequences,i=1,2,n=1,2,···,such that for n ≥2 Obviously, We claim that the sequences,i=1,2 are strictly decreasing,and the sequencesi=1,2 are strictly increasing. To proof this claim,we will carry out by induction.Firstly,from(3.16)and(3.29)we have Let us assume now that our claim is true for n,that is, Then From(3.32)and the expression of,it immediately follows that From(3.34)and the expression ofit immediately follows that The above analysis shows thati=1,2 are strictly decreasing,and the sequencesi=1,2 are strictly increasing.Therefore, Letting n →+∞in(3.30),we obtain Already,Theorem 3.1 shows that under assumption(3.1),(3.37)has a unique positive solution E∗(x∗,y∗).Hence,we conclude that that is Thus,the unique interior equilibrium E∗(x∗,y∗)is globally attractive. This completes the proof of Theorem 3.2. As a direct corollary of Theorem 3.2,we have: Theorem 3.3Assume that A1>0,where A1is defined by(3.5),assume further that r1>q/m1,then system(1.1)admits a unique positive equilibrium E∗(x∗,y∗),which is globally attractive. ProofNoting that under the assumption A1>0 and r1>q/m1,system(3.37)admits a unique positive solution E∗(x∗,y∗).The rest of the proof is the same as that of Theorem 3.2,and we omit the detail here. Example 4.1Consider the following system Here,corresponding to system(1.1),we take r1=b1=E=r2=b2=a2=k1=k2=1,m1=m2=0.5,q=2,a1=2.In this case,by simple computation,one could easily see that holds,that is,condition(2.13)in Corollary 2.1 holds,and so,it follows from Corollary 2.1 that the boundary equilibrium(0,0.5)of the system is globally stable.Numeric simulation(Figure 1)supports this assertion. Figure 1:Dynamic behaviors of system(4.1),the initial condition(x(0),y(0))=(3,0.5),(2,2),(0.5,2)and(3,0.2),respectively. Example 4.2Consider the following system Here,corresponding to system(1.1),we take r1=b1=a1=q=E=r2=b2=a2=k1=1,k2=4,m1=4,m2=0.5.In this case,by simple computation,one could easily see that holds,that is,condition(3.1)in Theorem 3.2 holds,and so,it follows from Theorem 3.2 that the unique positive equilibrium(0.493 215 759 3,0.817 957 268 8)of the system is globally stable.Numeric simulation(Figure 2)supports this assertion. Figure 2:Dynamic behaviors of system(4.3),the initial condition(x(0),y(0))=(3,0.5),(2,2),(0.5,2)and(3,0.2),respectively. Though there are many works on cooperative system([1-30]),only recently did scholars([2,3,25–27,29])began to study the cooperative or commensal system incorporating harvesting,however,as was shown in the introduction section,both Xie,Chen and Xue[2]and Lei[27]were consider the linear harvesting,and still no scholars investigate the cooperative system with nonlinear harvesting,this motivated us to propose system(1.1). We first show that overfishing may lead to the extinction of the species. Such kind of property is reflect by the catchablity coefficient q and constant m1,if q is too large,while m1is limited,then inequality(2.1)always holds,consequently,the first species will be driven to extinction. Our next result is concerned with the global attractivity of the positive equilibrium.Condition(3.1)shows that if b1k2larger then the intrinsic birth rate of the first species,also,if the harvesting is limited,such that r1>q/m1holds,then the two species could be coexist in a stable state.Generally speaking,to overcome the influence of harvesting,increasing the intrinsic rate is a necessary countermeasure.However,our study shows that it also need to restrict the intrinsic rate to satisfy the inequality r1
2 Extinction of the First Species
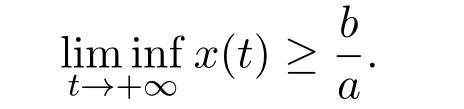
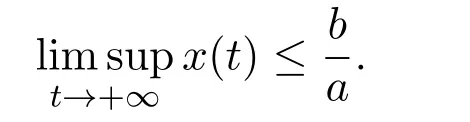

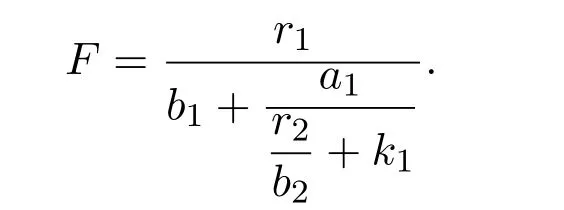
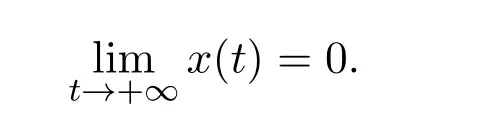




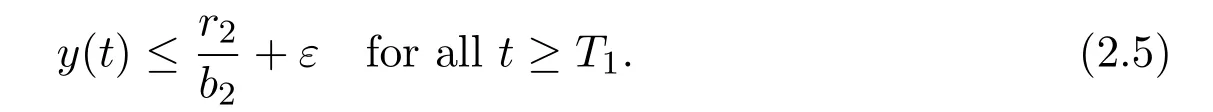
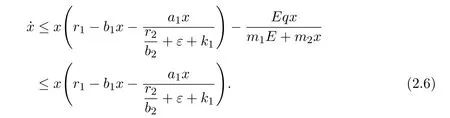

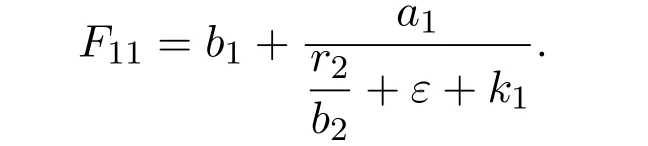


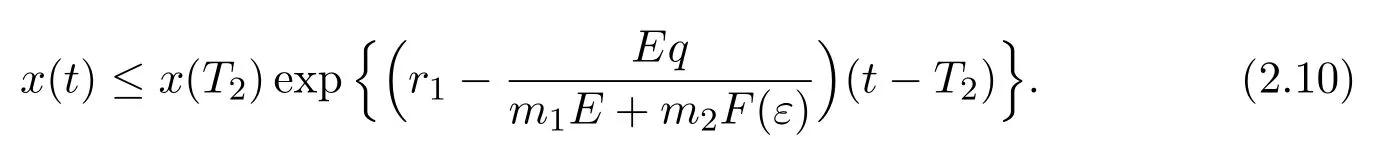
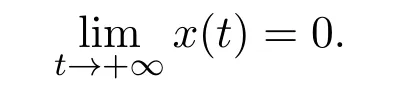



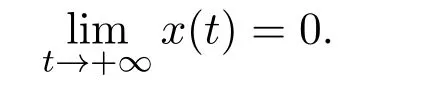

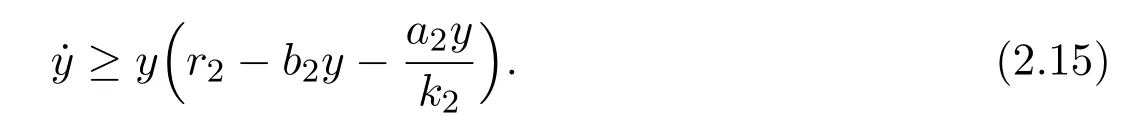
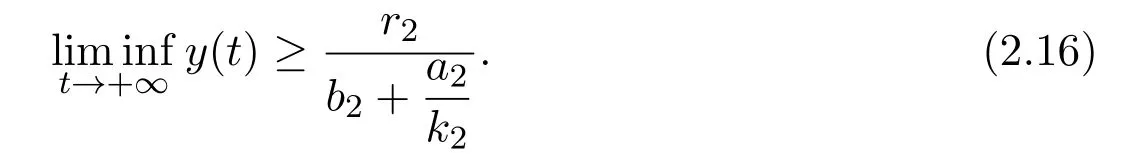

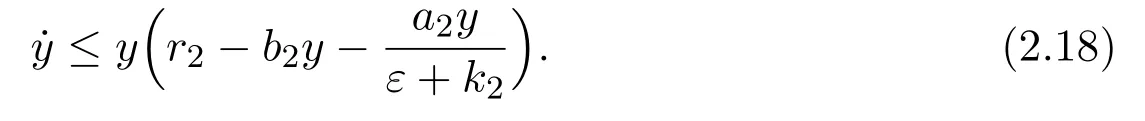
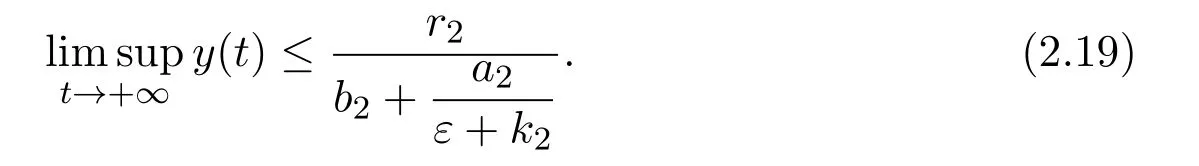


3 Stability of the Positive Equilibrium

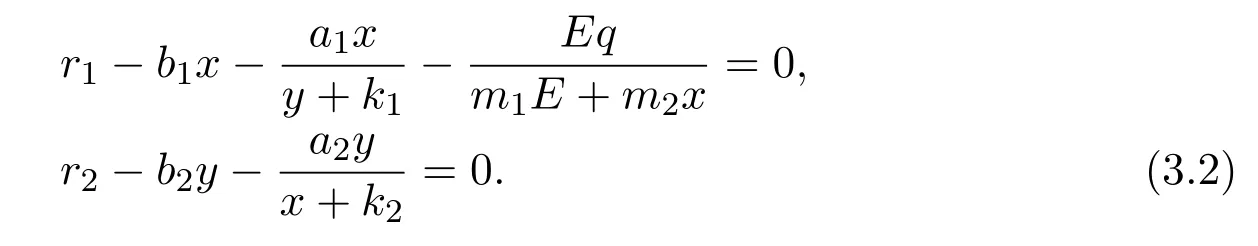
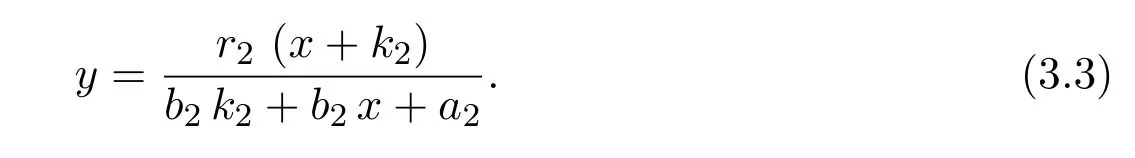

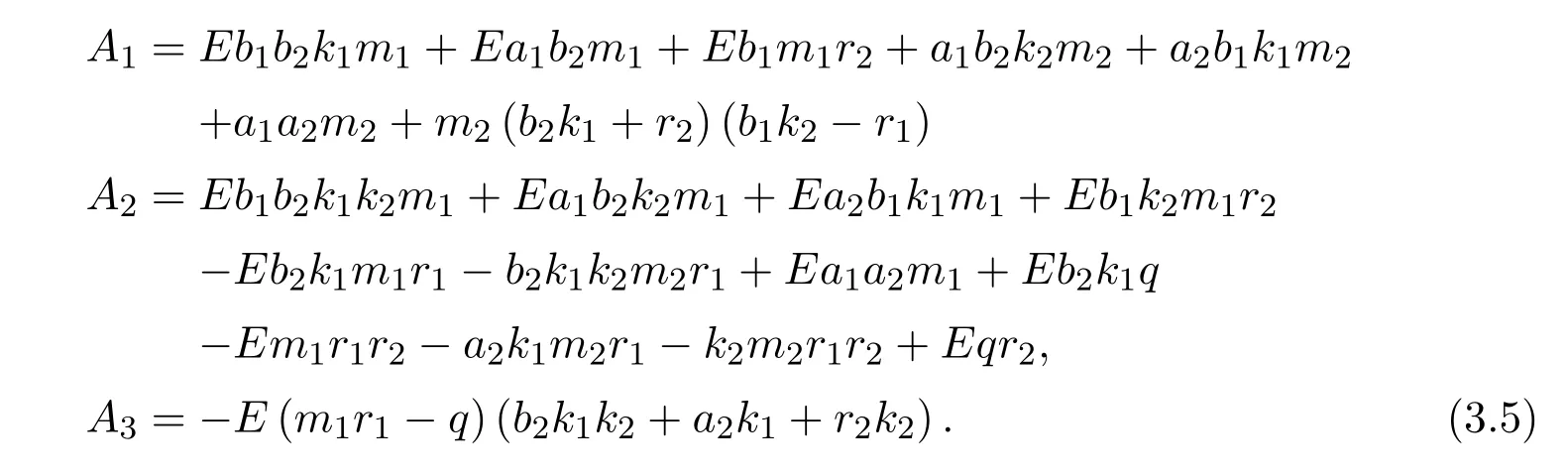
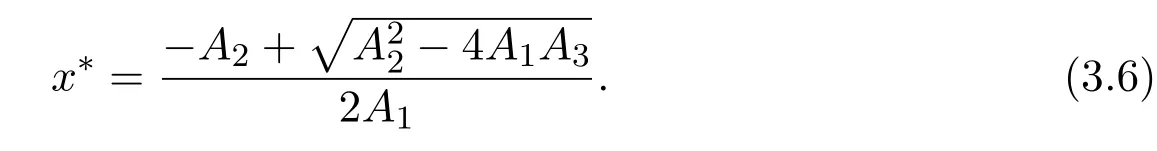

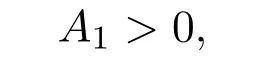

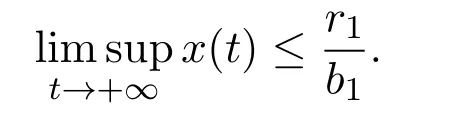
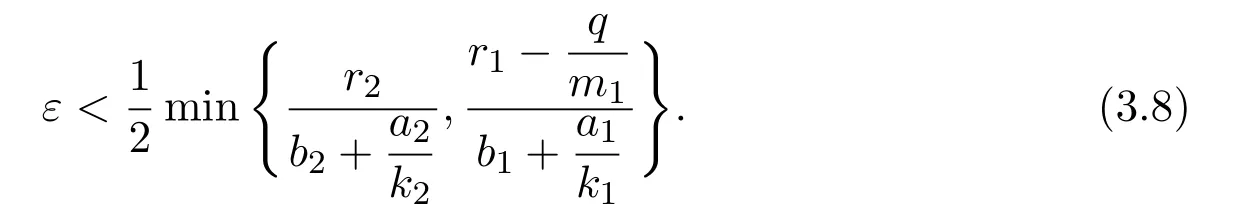
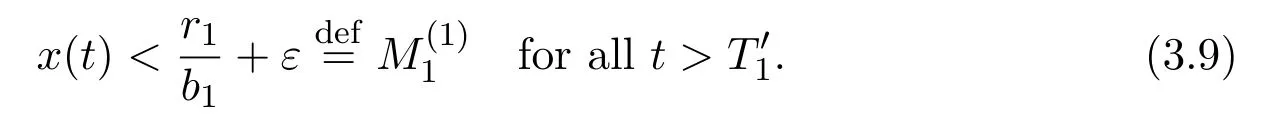
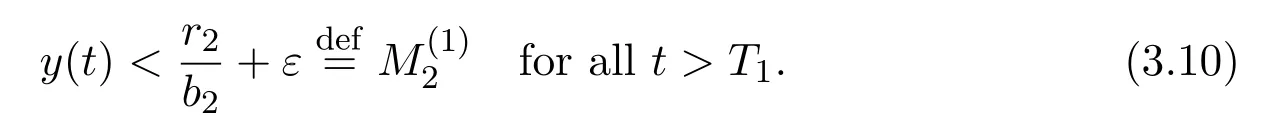
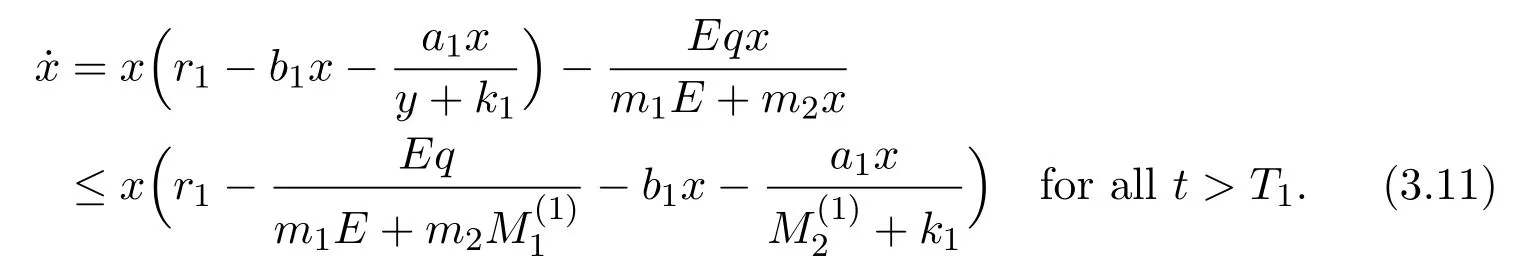
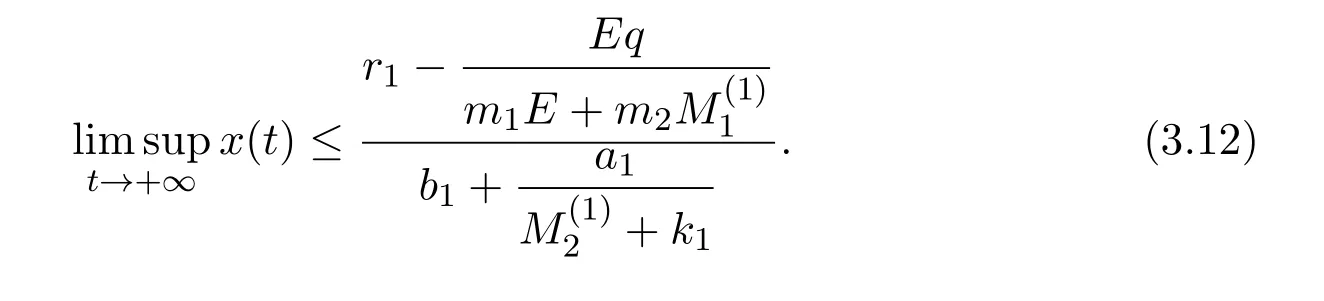
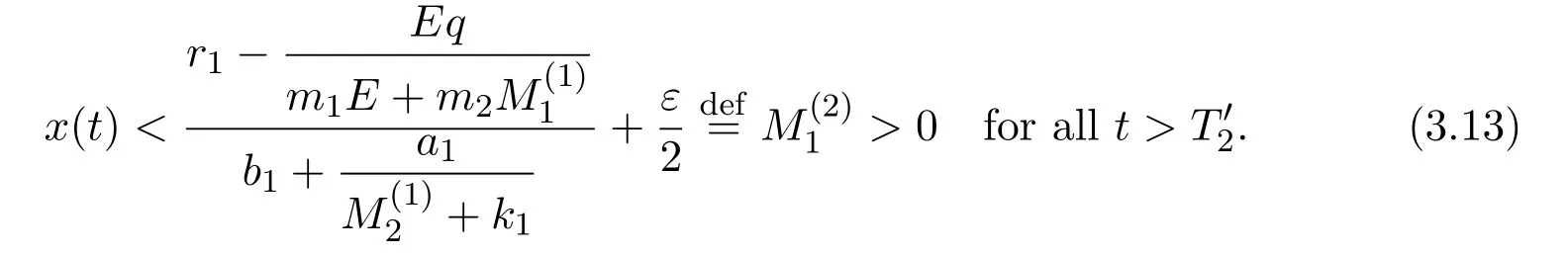
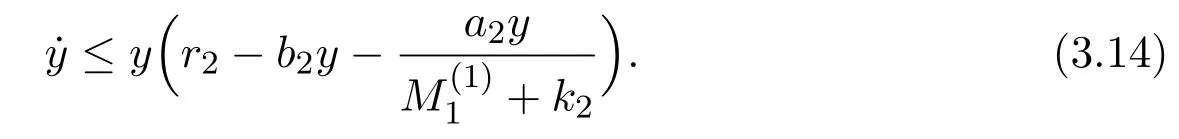
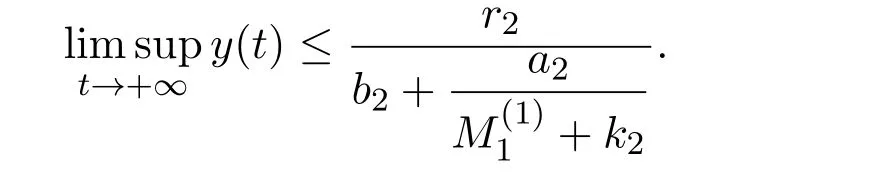


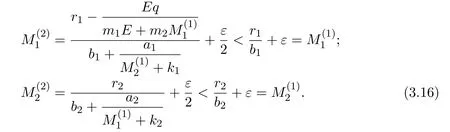
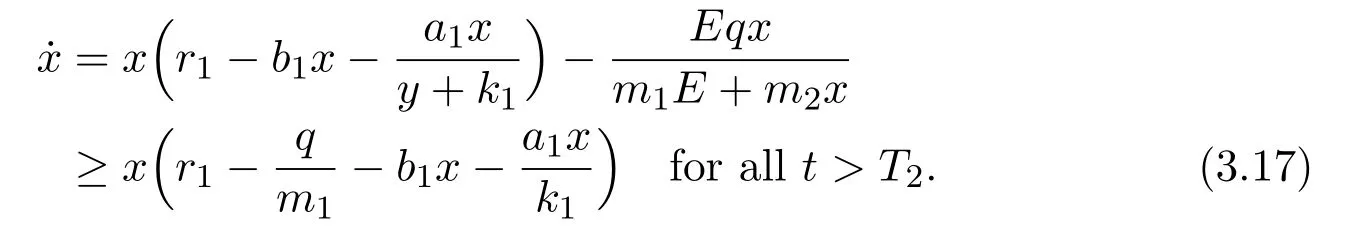
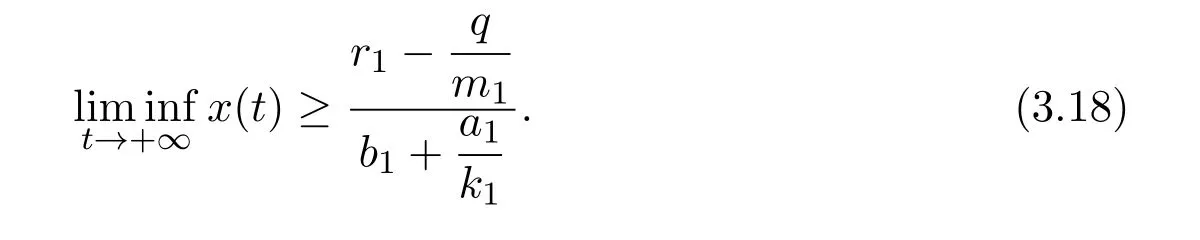
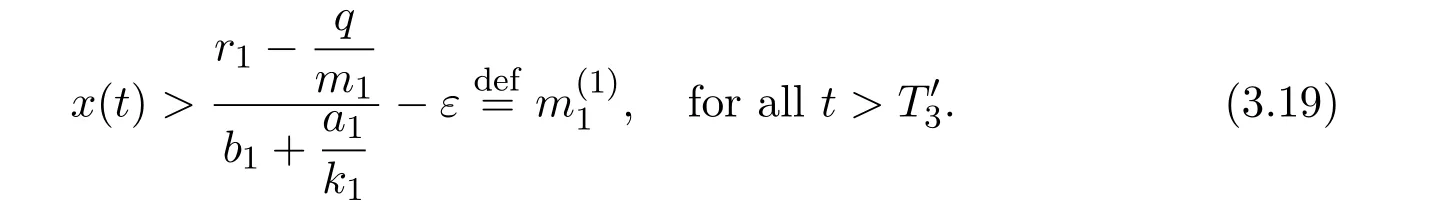
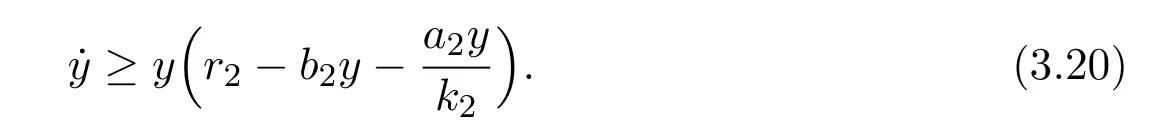

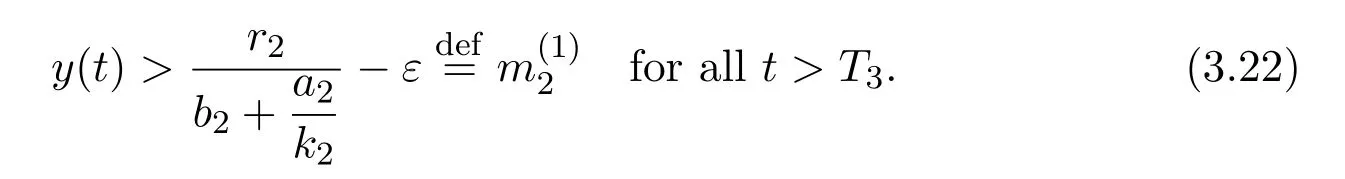
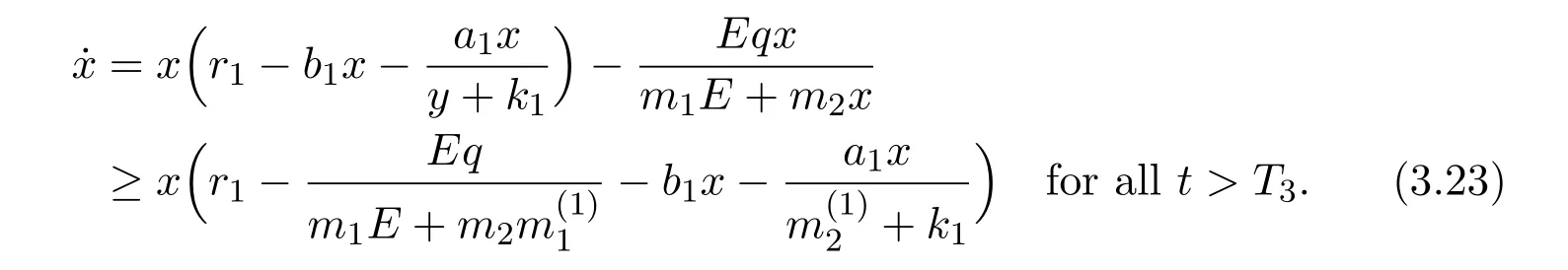
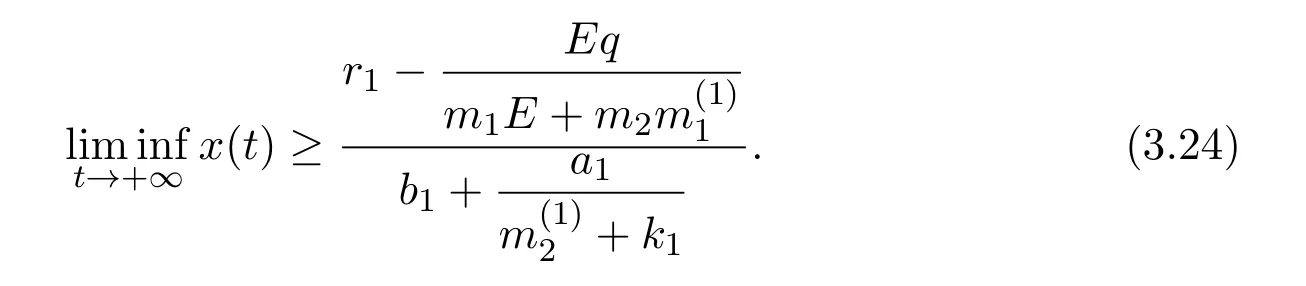
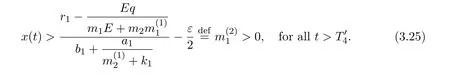
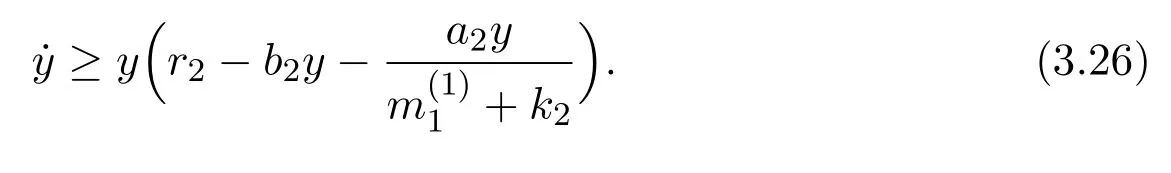

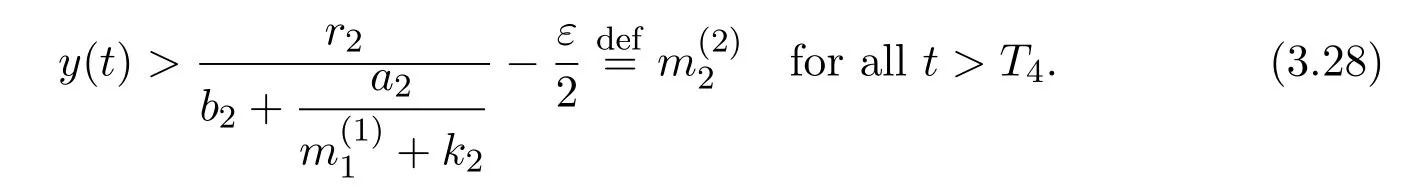
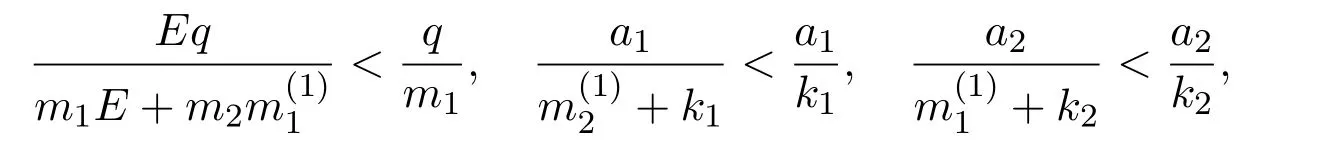
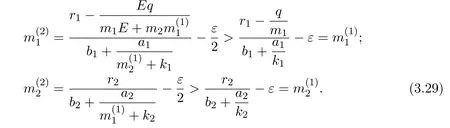
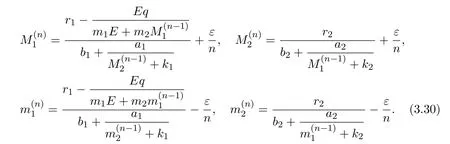
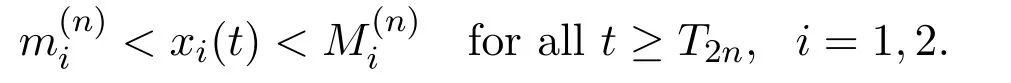

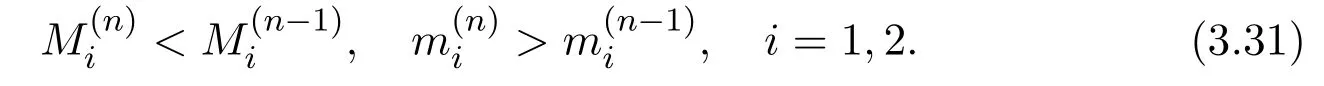
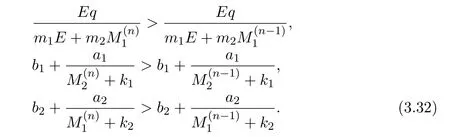


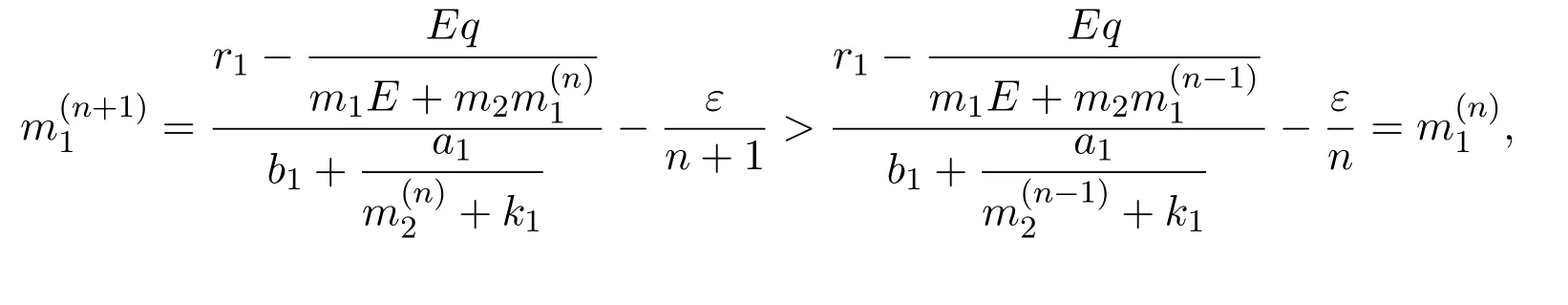
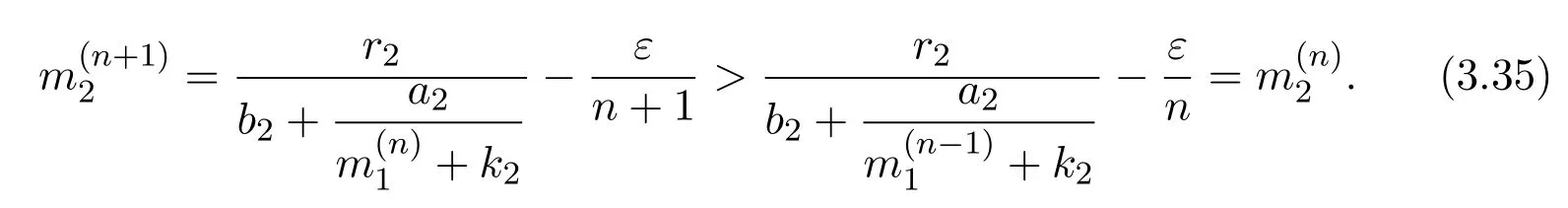
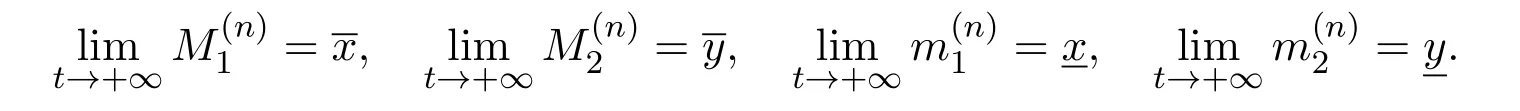
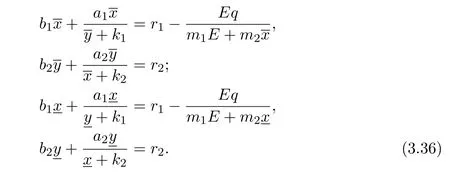
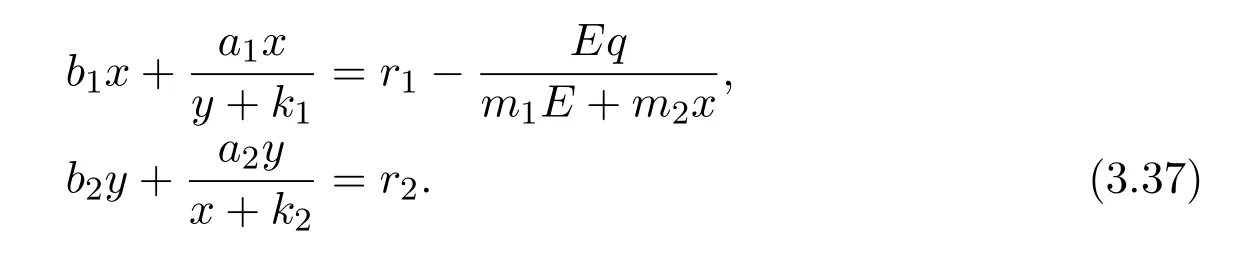
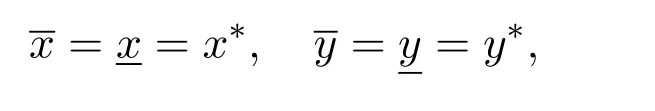
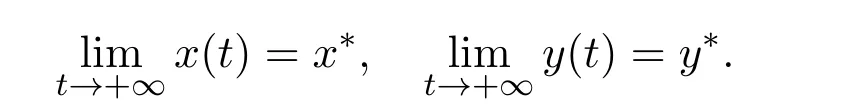
4 Numeric Simulations

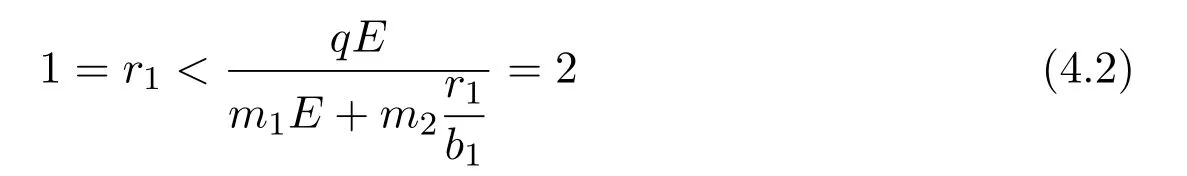
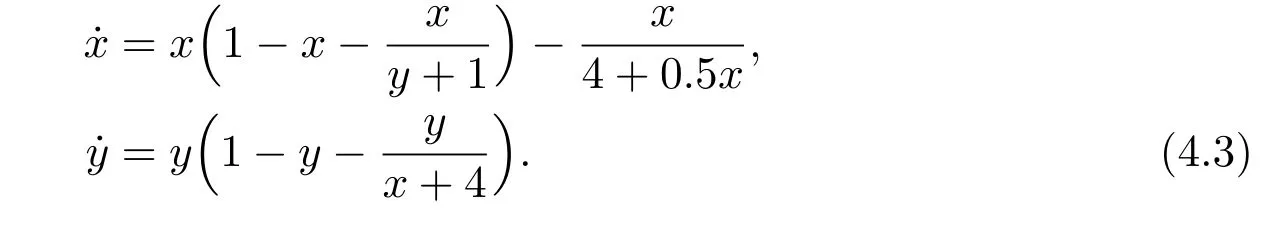
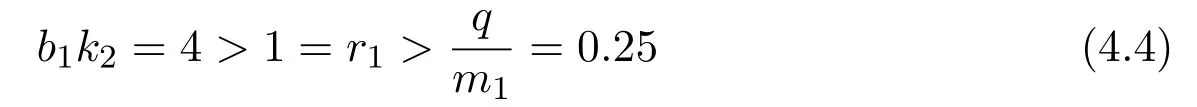
5 Discussion
 Annals of Applied Mathematics2019年4期
Annals of Applied Mathematics2019年4期
