基于先验信息的弹药消耗量统计推断方法*

赵汝东,史宪铭,姜广胜,2,李正映,李 康

(1.陆军工程大学石家庄校区装备指挥与管理系,河北 石家庄 050003;2.陆军步兵学院石家庄校区,河北 石家庄 050003)

目前弹药消耗预测主要依赖于对历史作战数据的运用,而新型弹药却面临着试验数据不足的问题，即缺少真实弹药消耗数据。因此,对新型弹药进行消耗预计只能借助由历史数据衍生出的专家经验值、试验仿真数据等先验信息。如何利用现有数据更精确地确定不同毁伤等级下的弹药消耗量是当前亟须解决的军事问题,也是弹药精确保障的关键。

现有的弹药消耗预测方法主要有基于数理模型,如任务量推算法[1]、时间序列分析法[2]、支持向量机[3]等,上述方法都要求有大量的数据支撑,其数据在可信性上需进一步探究;基于作战模拟,如兰彻斯特方程[4]、系统动力学[5]、作战仿真法[6]等,该类方法只能粗糙预测弹药消耗情况,准确性较低;基于智能算法,如BP神经网络[7-8]等,同样需要大量的弹药消耗数据,对统计数据的可靠性依赖大,上述方法均未考虑新型弹药消耗数据可信性验证的问题。如何保证现有弹药消耗数据在可信范围之内,以尽可能准确地预计达到各毁伤等级所需弹药量是当前研究的重点。

为了解决统计数据估计值可信性问题,学者们进行了区间估计,引入置信区间将其限定在一定范围内。赵洪宝[9]等利用数理统计理论对岩样单轴抗压强度置信区间、置信度等问题进行了系统的分析研究,整理并推导出了岩样单轴抗压强度“区间估计指标”的理论计算公式;王娟[10]等研究了极大似然估计的渐近正态性法和轮廓似然函数法,求解了Pareto分布中尺度参数的置信区间。徐晓岭[11]等在全样本、定数截尾样本以及缺失数据场合下,分别研究了位置参数、刻度参数的点估计与区间估计问题。

针对新型弹药历史消耗数据不足、预测精度较低等问题,本文利用先验信息对不同毁伤等级下弹药消耗量总体均值进行极大似然估计,得到确切的弹药消耗量值;并结合弹药消耗量分布情况对其均值进行区间估计,确定不同毁伤等级下弹药消耗量合理的置信区间,进一步缩小范围扩大精度,检验了极大似然估计值的可信性。应用分析验证了该方法是有效的。

1 基于截尾样本的最大似然估计

为了满足弹药精确保障要求,需预计出不同毁伤等级下弹药具体消耗情况,故对不同毁伤等级下弹药消耗量θ进行合理点估计。专家数据、试验仿真数据等先验信息经初步处理后,构建不同毁伤等级下的弹药消耗量置信总体Θ,对其样本进行极大似然估计[12],取到样本η1,η2,…,ηn的概率L(θ)最大,此时不同毁伤等级下弹药消耗量θ的估计值较为合理。

样本η1,η2,…,ηn的联合概率密度为

(1)

样本的似然函数表示为

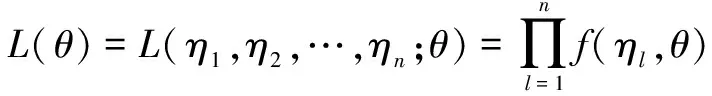
(2)

(3)

(4)

(5)

(6)

(7)

2 弹药消耗量的区间估计指标

2.1 先验信息下的弹药消耗分布规律

2.2 确定置信区间

根据数理统计原理,将置信度为1-α时不同毁伤等级下弹药消耗量总体均值μσi的置信区间[15]定义为

μδi=[δi-low,δi-high]

(8)

其中i代表不同毁伤等级,δi-low为不同毁伤等级下弹药消耗量总体均值的置信下限,δi-high为不同毁伤等级下弹药消耗量总体均值的置信下限。

(9)

由t分布的分位数定义知

(10)

即

从而可以确定不同毁伤等级下弹药消耗量总体均值μσi的一个置信水平为1-α的置信区间为

(11)

其中,不同毁伤等级下弹药消耗量样本标准差Si的计算公式为

(12)

3 应用分析

通过咨询相关领域专家，查阅文献资料得到了以下数据资料:表1是根据以往弹药实弹试验数据获得的专家经验值,6个目标装备达到轻度毁伤L1、中度毁伤L2、重度毁伤L3、报废L4时的弹药消耗量,取其均值作为单个目标达到不同毁伤等级下的弹药消耗量。认为零毁伤即目标未被命中,故不考虑零毁伤的情况。

表1 目标装备在不同打击强度下的战损率对比

在表1专家数据的基础上,对单个目标达到不同毁伤等级下的弹药消耗量进行仿真模拟,数据样本如表2所示,并展开统计推断研究。

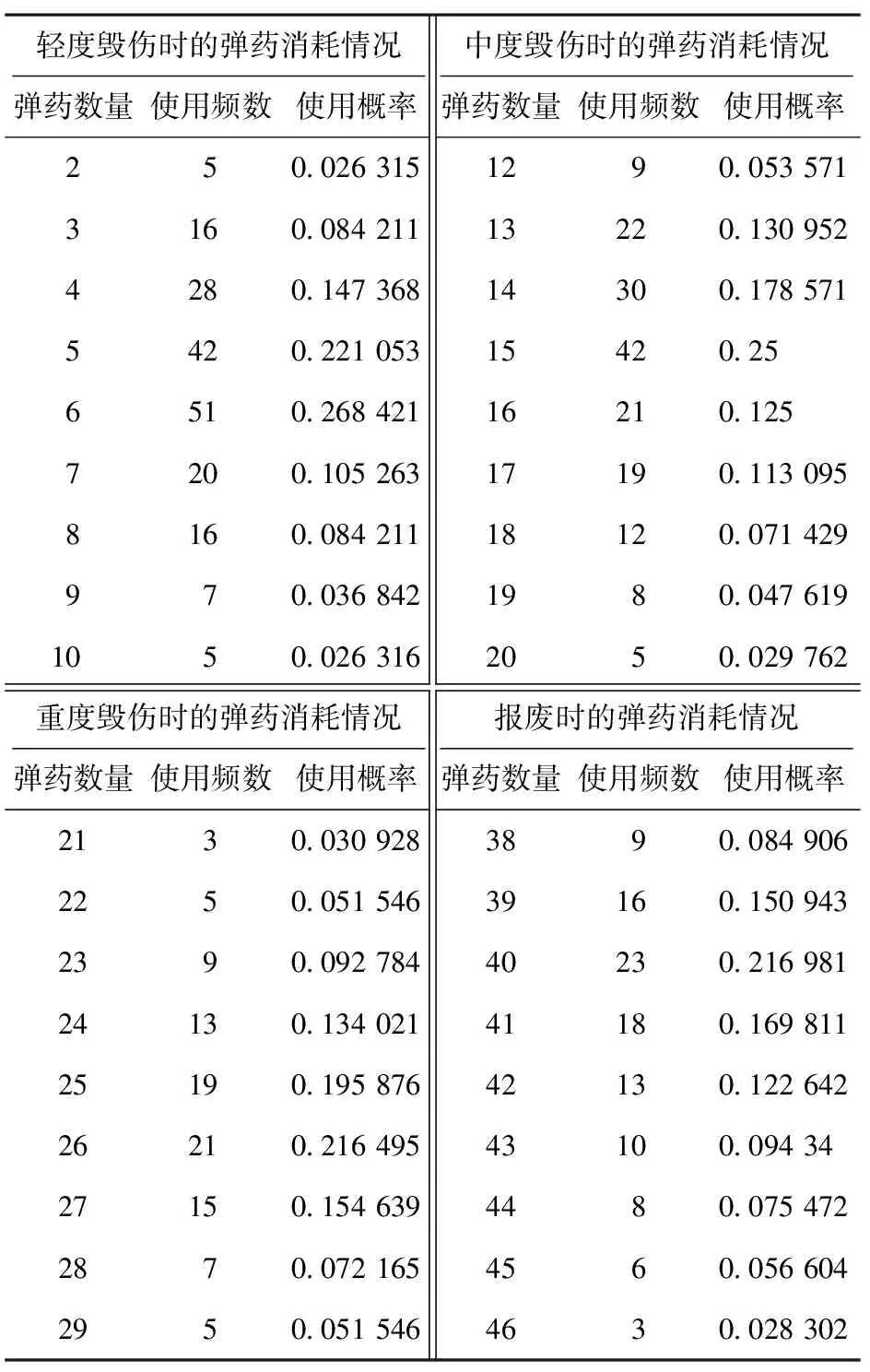
表2 目标装备达到各级毁伤时的弹药消耗情况

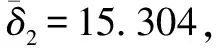
(13)

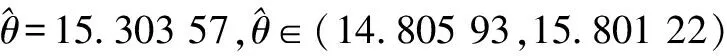
表3 目标装备达到各级毁伤

毁伤等级为零毁伤L0时,目标装备的作战效能损失不足5%。根据上述数据借助Origin8.0软件可以拟合出目标达到不同毁伤等级时的弹药消耗量曲线,如图1所示,更直观看到不同毁伤等级下的弹药消耗量变化趋势。

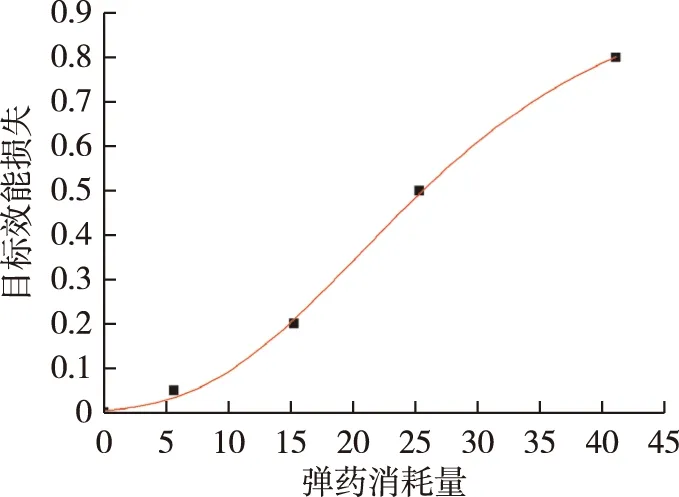
图1 不同毁伤等级下的弹药消耗量曲线

4 结束语

本文从数理统计原理出发,借助极大似然估计确定了不同毁伤等级下的弹药消耗量,并利用弹药消耗量总体均值的区间估计确定合理的置信区间,检验了不同毁伤等级下弹药消耗量的可信性。通过应用研究对此方法进行了验证,拟合出了目标达到不同毁伤等级时的弹药消耗量曲线,可为弹药保障决策提供指导,具有重要军事意义。接下来的研究需探索一种能在数据较少条件下进行弹药需求预计的方法,为新型弹药消耗预计提供新思路。