女装肩部结构变化与袖窿夹角的相关性

李 杨， 申 鸿， 吴 晶

(四川大学 轻工科学与工程学院， 四川 成都 610065)

服装肩部是前后衣片及衣领、衣袖的连接处，其结构设计不仅影响自身造型，也影响领与袖的造型[1]，甚至还会影响到服装穿着舒适性以及服装整体穿着效果[2]，因此，肩部结构平衡在整个上衣结构设计中至关重要。肩部肌肉主要由斜方肌、胸锁乳突肌、下三角肌构成[3]，肩部结构主要受肩宽、肩斜度、肩线3个要素影响。肩斜度是人体肩部由上到下呈现的倾斜度，即颈侧点与肩点两点连线与水平线的夹角[4]，是决定肩部造型结构的重要因素。

目前，学术界对肩部的研究主要集中在肩宽、肩斜度以及对服装整体造型的影响方面[5]，关于肩部结构与袖窿结构的关系方面的研究很少。虽然李钊[6]依据肩部评价参数建立模型，研究了肩宽对衣身和衣袖的设计影响，但并未涉及肩斜度与袖窿结构的研究。

袖窿夹角是袖窿结构中的重要参数，探究肩部结构变化与袖窿夹角的相关性使得肩部与袖窿之间的关系得以量化。本文通过实验及数据统计回归分析，运用数理方法得到女装肩斜度与袖窿夹角度数的线性回归方程，研究了肩部造型与袖窿结构参数之间的关系，以期为女装肩部造型设计提供思路与方向。

1 实验部分

1.1 实验材料

160/84A标准人台、服装垫肩(厚度H为0.5、1.0、1.5、2.0、2.5 cm)、幅宽为158 cm的纯棉白坯布、剪刀、珠针、量角器、画粉、放码尺，均为专业实验室标准化材料。

1.2 实验方法及步骤

在160/84A的标准人台上用立体裁剪的方法分别裁剪出垫肩厚度分别为0、0.5、1.0、1.5、2.0、2.5 cm的合体上衣片，如图1所示。

图1 不同垫肩厚度的合体衣片Fig.1 Fitted pieces with different thicknesses of shoulder pads

将人台上的衣片取下，得到6种垫肩厚度条件下的衣片平面展开纸样(编号为P1、P2、P3、P4、P5、P6)，分别测量出其肩斜角、袖窿夹角，测量方法如图2所示。

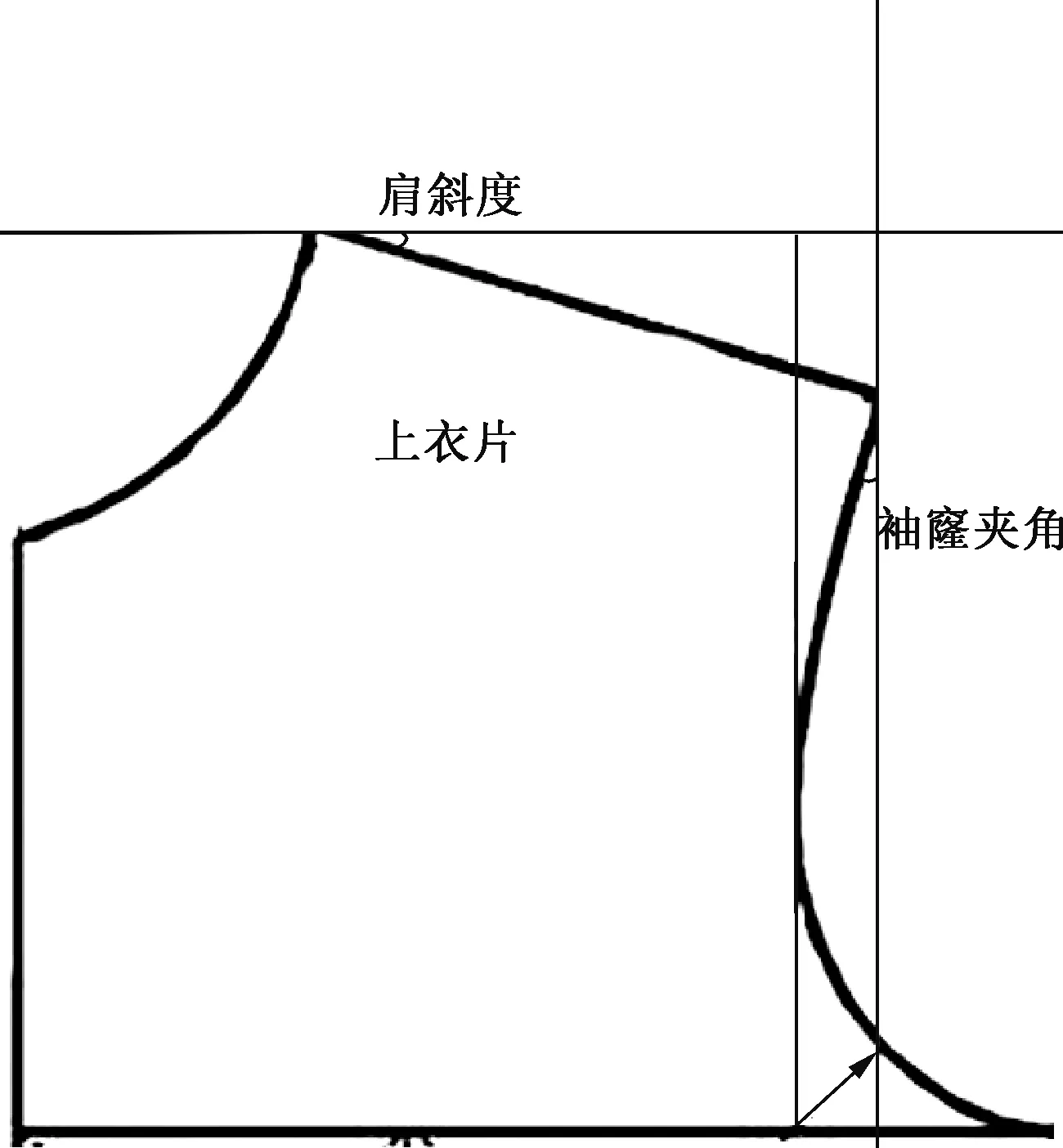
图2 肩斜度与袖窿夹角的测量方法Fig.2 Method for measuring shoulder slopes and armhole angles

GB/T 16160—2008《服装用人体测量的部位与方法》中没有将肩斜度列入测量部位[7]，在肩部结构研究领域，直接在平面展开纸样中测量部位角度仍是获取肩斜度最为直观而精确的方式。日本文化式原型中的肩斜度也是通过立体裁剪得到合身的原型衣，从平面展开纸样上测量肩部角度，通过统计大量数据而得的[8]，这种测量方法有利于对人体结构和设计原理的深入研究，数据统计所得的实验结果相较其他方法有着明显的优势[9]。

2 实验结果与分析

2.1 数据统计分析

通过测量，得到P1～P6的6组数据，每组数据包含垫肩厚度、肩斜度以及袖窿夹角，如表1所示。

表1 测量P1～ P6所得肩斜度与袖窿夹角值Tab.1 Shoulder slopes and armhole angles of P1～ P6

从表1数据可看出，随着垫肩厚度的增加，肩斜度与袖窿夹角均呈降低的趋势。肩斜度的变化也直接影响着袖窿夹角的变化趋势，但二者是否存在线性相关关系，还有待对数据进行进一步分析。

2.2 实验数据相关性分析

肩斜度与垫肩厚度的相关性如图3所示。根据图中的6个实验点数据分布, 通过回归分析，可以判断垫肩厚度与肩斜度之间存在线性相关关系。通过运用最小平方法原理求解2个待定系数，得到肩斜度与垫肩厚度的线性拟合关系：y=18.24-4.86x，可决系数R2=0.931 3。可见，二者的线性相关关系具有较高的拟合精度。

图3 肩斜度与垫肩厚度的相关性分析Fig.3 Correlation analysis between shoulder slopes and shoulder pads thicknesses

图4示出袖窿夹角与肩斜度的相关性。根据图中的6个实验点数据的分布，经回归分析，可以判断袖窿夹角与肩斜度之间存在正相关关系。通过计算2个待定系数，得到袖窿夹角度数与肩斜度之间的线性拟合关系：y=7.73+0.91x，可决系数R2=0.934 3。该线性相关关系拟合精度较高。

图4 袖窿夹角与肩斜度的相关性分析Fig.4 Correlation analysis between armhole angles and shoulder slopes

2.3 实验结果应用分析

为保证测量结果的准确性与科学性，选择了与人体测量要求一致的人台作为实验测量对象，符合人体直立状态下双手下垂、肩部放松的测量条件，同时有效避免了测量中由于人体不稳定性造成的误差，并在保证服装合体性的前提下进行测量，从而保证了实验结果的科学性。

在实际应用中，由于人体体型特征的个体差异性较大，服装肩部结构不仅受人体肩斜度影响，还与人体体型密切相关，任何一般性的实验结果均不能直接适用于所有体型。BMI指数为体重(kg)与身高(m)平方的比值[10]，被认为是评价人体肥胖程度的指标，常作为人体体型特征的重要参数。根据前期研究，衣身肩斜度与人体肩斜度及BMI指数三者的线性回归关系为：衣身肩斜度=11.853+0.294×人体肩斜度+0.135×BMI指数[11]。利用该回归关系，可以简便地获取每个人体的衣身肩斜度。在此基础上，运用本文得出的线性回归关系计算出不同体型的人体所需的垫肩厚度，从而实现了本文研究结果应用的普适性。同时，通过3个线性回归方程的代入计算，能够建立起人体体型与袖窿夹角之间的关系，在服装制版中，只需知道人体身高、体重及肩斜度信息，即可通过计算获取袖窿夹角，从而提高了袖部结构设计的效率与准确性。

为验证运用本文实验结果进行袖部结构设计的准确性，选取5位成年女性的体型数据(身高、体重、人体肩斜度)作为实验样本(编号为T1、T2、T3、T4、T5)，首先运用衣身肩斜度与人体肩斜度及BMI指数三者的线性回归关系计算出5个样本的衣身肩斜度；在此基础上，运用袖窿夹角与衣身肩斜度的线性回归关系y=7.73+0.91x分别计算其袖窿夹角，计算结果如表2所示。

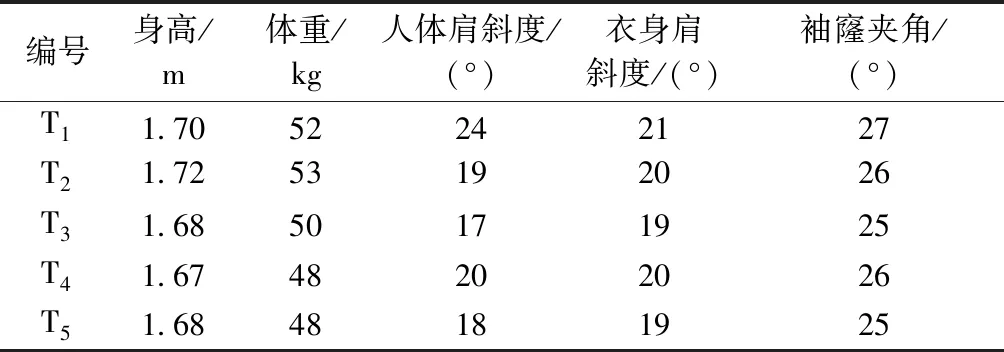
表2 T1～ T5的衣身肩斜度与袖窿夹角Tab.2 Garment shoulder slopes and armhole angles of T1～ T5

根据计算结果，分别绘制T1～T5的1/4平面结构图，借助衣身肩斜度确定肩端点位置，并根据袖窿夹角直接确定袖窿弧线弧度。运用平面裁剪的方法制作成衣，分别由T1～T5数据样本所对应的5位成年女性试穿，试穿结果显示：成衣肩部、袖窿部位合体度较高，肩部与袖部连接处平顺，无肩端点、颈侧点浮起等现象。由此可见，运用本文实验结果中的线性回归方程能够提升数据计算与结构制图的效率，且数据相对准确，在袖部结构设计方面具有实用价值。

在服装结构设计中，肩部与袖部的结构往往被作为完全独立的2个部分，由于欠缺肩部与袖部连接部位的整体设计及对二者关系的考虑，运用传统的比例制图法进行结构设计容易出现成衣不合体的问题。同样参照 T1～ T5样本的体型数据，运用传统比例制图法绘制1/4平面结构图，通过比例计算间接得到肩端点位置与袖窿弧线弧度，运用平面裁剪的方法制作成衣，分别由T1～ T5数据样本所对应的5位成年女性试穿，并与前一实验中的成衣试穿效果进行比较，结果显示：这次实验中的成衣合体度明显低于前一实验，尤其是袖部与肩部连接处出现了肩端点轻微浮起的现象。

综上所述，相对于传统单一的比例制图方法，运用本文实验结果中的线性回归关系辅助比例制图法进行结构设计能够有效改善肩部袖部的合体性，提升服装整体结构设计水平。

3 结束语

服装肩部结构直接影响着上衣整体风格，而肩斜度、袖窿夹角均为肩部结构的重要影响因子。肩斜度过大则使肩线在颈侧点浮起，在肩端点处与人体肩部接触，导致服装在人体肩端处集中受压，服装整体缺少稳定性；肩斜度过小则使肩线在颈侧点接触，在肩端点处浮起，可能导致服装在人体颈部集中受压。袖窿夹角则直接影响肩部外轮廓造型，袖窿夹角越小，肩部造型相对越宽松；袖窿夹角越大，肩部造型相对越合体。垫肩厚度与肩斜度之间存在线性相关关系，线性回归方程为y=18.24-4.86x，即在运用垫肩进行女装肩部造型设计的过程中，随着垫肩厚度的增加，肩斜度呈有规律的下降趋势。运用二者的线性关系，能够推算出达到一定肩斜度所需的垫肩厚度，并将垫肩的使用对肩部结构的影响进行量化，对肩部造型设计尤其是创意立体造型的设计具有参考价值。

袖窿夹角度数与肩斜度呈线性正相关关系，线性回归方程为y=7.73+0.91x，即随着女装肩部造型的变化，肩斜度发生改变，当肩斜度增大时，袖窿夹角也随之有规律地增大，同时导致整个袖部结构的变化。二者的线性相关关系使肩部与袖窿之间的变化关系得以量化，运用该线性关系，可以将袖窿夹角作为一个突破口，有助于深入研究服装肩部与袖窿参数之间的关系，运用线性关系能够对2个部位的结构参数进行验证，从而提高制图的精确度。

FZXB