第一性原理研究half-Heusler合金CoVTe和FeVTe半金属性及磁性的稳定性
姚仲瑜,曾 腾,朱暑波, 林 红
(1. 海南师范大学 物理与电子工程学院,海口571158; 2. 海南省农垦中学,海口570226)
1 引 言
半金属(Half metal)是指一个自旋方向的电子能带具有金属性而另一个自旋方向的电子能带是半导体性或绝缘体性的物质. 材料的半金属性是de Groot 等人对half-Heusler 合金NiMnSb 和PtMnSb的能带结构计算时首次发现的[1]. 自从de Groot发现材料的半金属性以来,已在理论和实验上发现多种结构的化合物具有半金属性,如铁磁性氧化物Fe3O4[2]和CrO2[3]、full-Heusler和half-Heusler合金[4-7]、钙钛矿稀土锰氧化物La0.7Sr0.3MnO3[8,9]、闪锌矿结构化合物[10]、双钙钛矿结构Sr2CrReO6[11]和岩盐结构化合物[12]等. 此外,研究还发现inverse-Heusler 合金 Ti2Co1-xNixGa具有半金属性[13]. 半金属是制作一代电子器件—自旋电子学器件(Spintronic device),如自旋二极管(Spin diode)、自旋三极管(Spin transistor)和自旋过滤器(Spin filter)等的重要材料[14].
近年来,半金属性half-Heusler合金的研究成为凝聚态领域的热点课题. 基于第一性原理的电子结构计算,Zhang等发现half-Heusler合金NiCrTe、NiCrSe和NiCrP是半金属性铁磁体,进一步的研究表明当晶格常数变化(相对于平衡晶格常数)在-1.5%—3%,0%—3.7% 和-3%—2%范围内时合金NiCrP、NiCrSe和NiCrTe仍能保持半金属性[15]. 他们对half-Heusler合金NiVAs的电子结构计算发现该合金也是半金属[16]. 2012年,Yao等人的电子结构计算结果表明half-Heusler合金CoCrP和CoCrAs是半金属铁磁体,它们具有较大的半金属隙(分别为0.46 eV和0.50 eV),同时晶格常数变化在-4.8%—6.6%和-7.7%—4.5%范围内时两合金的半金属性保持不变[6]. 此外,理论计算还预言一组Te族half-Heusler合金[17]以及无过渡金属元素half-Heusler合金GeKCa和SnKCa都具有半金属性[18].
在自旋电子学器件的制作过程中,通常要在器件基底上外延生长一层或多层半金属材料薄膜. 在半金属材料的合成以及器件的制作过程中,通常都会伴随着晶体晶格的形变. 理论计算研究表明,在发生晶体晶格均匀形变的情况下,一些半金属材料的半金属性会消失,从而呈现出金属性[6, 19]. 作为制作自旋电子学器件的重要材料,半金属材料的性质稳定对于自旋电子器件的研制至关重要,因此,本文构建half-Heusler合金CVTe和FeVTe,并将以晶格均匀形变作为晶格形变模型,采用第一性原理的全势能线性缀加平面波(Eull-potential linearized augmented plane wave,FP_LAPW)方法,计算half-Heusler合金CoVTe 和FeVTe的电子结构,进而研究其半金属性和磁性的稳定性. 该研究能从一个侧面反映晶体晶格形变对以上两种合金的半金属性和磁性的影响.
2 晶体结构模型与计算方法
本文采用WIEN2k[20]软件包计算half-Heusler合金CoVTe和FeVTe的电子结构. 该软件的程序设计采用了基于密度泛函理论为基础的FP_LAPW方法. 在对波函数的描述中,该方法采用糕饼(Muffin-tin)模型将晶体晶胞空间分为二个区域:非重叠原子球区和间隙空间区. 在原子球面内的势能函数和电荷密度分布有近似的球对称性,基函数取球谐函数和径向函数的乘积;在间隙空间区的势能变化比较平缓,电子波函数用平面波基矢展式表示. 在电子结构计算中,截断参数取RMT×Kmax=8, 其中,Kmax是平面波展式中最大的倒格子矢量,RMT是最小的糕模原子球半径. 电子的交换-关联势能采用Perdew等[21]提出的广义梯度近似(Generalized gradient approximation, GGA)的Perdew-Burke-Ernzerhof 96方法处理.Co、Fe、V和Te的原子球半径分别取2.1、2.1、2.0和2.4 a.u.(a.u.为原子单位. 1 a.u. = 0.529177 Å). 波矢积分采用四面体网格法,第一布里渊区k点网格取11×11×11. 自洽计算的收敛标准取每晶胞1.0×10-4e.

图1 Heusler-Heusler合金CoVTe的晶体结构Fig. 1 Crystal structure of the half-Heusler alloy CoVTe.
3 结果与讨论
3.1 Heusler-Heusler合金CoVTe和FeVTe半金属性的稳定性
对half-Heusler合金CoVTe和FeVTe(平衡晶格常数分别为5.88 Å和5.82 Å[17])的电子结构进行自旋极化计算,电子的态密度(density of states,DOS)分布如图2所示. 从图2中可以看出,合金CoVTe和FeVTe自旋向上电子的态密度在费米能处是连续分布的,因而自旋向上电子的能带具有金属性,同时,两合金自旋向下电子的态密度分布在费米能处都形成了能隙,自旋向下电子能带具有非金属性,因此,两合金都是半金属. 在CoVTe和FeVTe自旋向下的DOS分布中(见图2),价带顶分别位于-0.91 eV和-1.12 eV, 导带底分别位于0.21 eV和0.20 eV,因此,两合金非金属性能带(自旋向下)带隙分别为1.12 eV和1.32 eV, 它们的半金属隙(half-metallic gap. 即,在非金属性能带中,费米能到价带顶的间距与费米能到导带底的间距中的最小者)分别为0.21 eV和0.20 eV.
在保持晶体结构空间群不变的情况下,本文用△a/a0表示晶体的晶格均匀形变(Uniform deformation). 其中,a0为晶体平衡时的晶格常数,a为形变后的晶格常数,Δa=a-a0. 使合金CoVTe和FeVTe的晶格均匀形变△a/a0限于±7%,在此范围内计算两合金的电子结构,研究晶格形变对它们的半金属性的影响.


图2 Half-Heusler合金CoVTe和FeVTe的自旋电子态密度以及Co、V、Fe和Te原子态密度: (a) CoVTe; (b) FeVTe. 费米能位于0 eV (用竖直虚线表示)Fig.2 Spin-dependent total DOS ofquaternary Heusler alloys CoVTe and FeVTe and DOSs of the atoms of Co, Fe, V and Te: (a) CoVTe; (b) FeVTe. The vertical dotted line indicates the Fermi level at 0 eV.
图3给出合金CoVTe和FeVTe晶格均匀体形变△a/a0取±7%时的电子态密度分布. 在图3中,合金CoVTe和FeVTe晶格均匀形变△a/a0分别为±7%时自旋向上的电子能带都是半金属性的,因此,它们是否具有半金属性完全取决于自旋向下电子能带的性质.对于自旋向下电子的DOS分布,从图3中可以看出:(1)当CoVTe的形变△a/a0为-7%和+7%时,费米能位于自旋向下DOS空白区内,该自旋方向电子的子能带具有非金属性,此时合金CoVTe呈现出半金属性;(2)当FeVTe的形变△a/a0为+7%时,很显然,自旋向下电子的能带是非金属性的,合金具有半金属性;当FeVTe的形变△a/a0为-7%时,因有少量自旋向下电子的DOS分布从右边穿过费米能,自旋向下电子的能带是金属性的,这时FeVTe呈现为金属性.
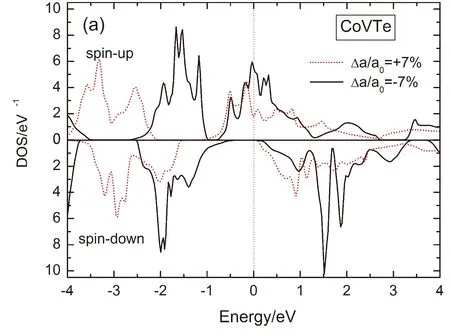
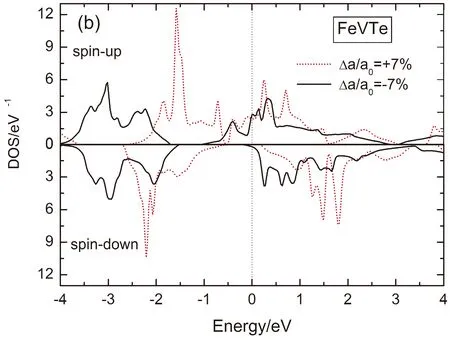
图3 Half-Heusler合金CoVTe和FeVTe晶格均匀形变△a/a0为±7%时的态密度分布: (a)CoVTe; (b)FeVTe. 费米能位于0 eV(虚线).Fig.3 The calculated spin-dependent DOSs of half-Heusler alloys CoVTe and FeVTe with △a/a0=±7%. The Fermi level is located at 0 eV.
为了进一步详细研究晶体均匀形变对合金半金属性的影响,使合金CoVTe和FeVTe的晶格均匀形变△a/a0在-7%~+7%之间变化,即晶格常数变化分别在0.547 nm-0.629 nm和0.541 nm-0.623 nm,在此范围内计算两合金的电子结构. 计算结果显示,在上述晶格常数的变化范围内,两合金自旋向上的电子能带是金属性的(未在此给出). 图4给出在费米能附近自旋向下电子能带的DOS空白区随晶格常数的变化关系. 从图4中看出,当晶格常数分别在0.547 nm — 0.629 nm和0.554 nm — 0.623 nm,即晶格均匀形变△a/a0分别在-7% — +7%和-4.8% — +7%时,合金CoVTe和FeVTe的费米能位于自旋向下DOS空白区内,它们在上述形变范围内具有半金属性. 对于合金FeVTe,当晶格常数小于0.554 nm时,费米能位于自旋向下的DOS空白区之外(见图4(b)),有自旋向下的电子能带穿过费米能,这样该自旋向下能带是金属性的,这时合金FeVTe由半金属性转变为金属性. 综合以上分析,当晶格均匀形变△a/a0分别为-7% — +7%和-4.8% — +7%时,half-Heusler合金CoVTe和FeVTe保持半金属性.


图4 Half-Heusler合金CoVTe和FeVTe费米能附近的自旋向下态密度空白区随晶格常数的变化关系. 图中的水平线段表示费米能附近的自旋向下电子态密度空白区域范围. 费米能位于0 eV. 水平虚线表示平衡晶格常数a0. Fig. 4 The blank in the spin-down DOSs of half-Heusler alloys CoVTe and FeVTe as a function of lattice constant. The horizontal straight lines correspond to the blank in the spin-down DOS. The Fermi level is located at 0 eV. The horizontal dotted line indicates the equilibrium lattice constant a0
3.2 Half-Heusler合金CoVTe和FeVTe磁性的稳定性
自旋极化的电子结构计算结果显示,晶格平衡时合金CoVTe和FeVTe的晶胞磁矩都是2.00 μB和1.00 μB. 两合金的整数晶胞总磁矩遵从关系式:M=(Z-18) μB[22],其中,M为分子总磁矩(单位为μB); Z为晶胞中各原子价电子数之和. 其中,Co、Fe、V和Te原子的价电子数分别为9(3d74s2)、8(3d64s2)、5(3d34s2)和6(5s25p4). 合金中各原子磁矩(自旋向上电子的自旋磁矩为正,自旋向下电子的自旋磁矩为负;原子磁矩为原子球内所有电子的净自旋磁矩)分别列于表1中. 在两合金中,过渡金属V的原子磁矩较强,sp主族元素Te的原子磁矩较弱,并且为负值(磁矩沿自旋向下方向). 两合金晶格平衡时晶胞总磁矩主要来源于过渡金属V的原子磁矩.
表1 合金CoVTe和FeVTe的晶胞总磁矩(Mtot)和各原子磁矩(Matom).
Table 1 Calculated total magnetic moment (Mtot) and atomic magnetic moments (Matom) of CoVTe and FeVTe.

CompoundMtot/μBMatom/μBXVTeCoVTe2.000.091.71-0.03FeVTe1.00-0.511.33-0.01

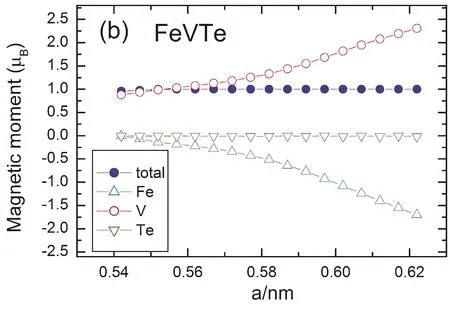
图5 合金CoVTe和FeVTe晶胞总磁矩和各原子磁矩随晶格常数的变化关系Fig.5 The total magnetic moment and atomic magnetic moments as function of lattice constant for CoVTe and FeVTe.
仍然使晶格均匀形变△a/a0在-7%~+7%之间变化,计算合金CoVTe和FeVTe的磁性,并在图6中给出合金晶胞总磁矩和各原子磁矩随晶格常数的变化关系. 在图6中可以看出,合金中各原子的磁矩随晶格常数的变化而变化. 计算结果显示,当晶格常数的变化分别在0.547 nm — 0.629 nm和0.554 nm — 0.623 nm,即晶格均匀形变△a/a0分别为-7% — +7%和-4.8% — +7%时,合金CoVTe和FeVTe晶胞总磁矩分别保持为整数磁矩2.00 μB和1.00 μB.
综上所述,在晶格均匀形变△a/a0分别为-7% — +7%和-4.8% — +7%时,合金CoVTe和FeVTe仍能保持半金属性,同时具有稳定的整数晶胞总磁矩. 在上述晶格形变范围内,两合金的半金属性与其晶胞总磁矩为整数是相互关联的.
4 结 论
运用基于第一性原理的FP_LAPW方法,计算half-Heusler合金CoVTe和FeVTe的电子结构. 计算结果表明,合金CoVTe和FeVTe处于晶格平衡时具有半金属性,半金属隙分别为0.21 eV和0.20 eV,合金晶胞总磁矩分别为2.00 μB和1.00 μB. 使合金晶格均匀形变△a/a0在-7%~+7%之间变化,在此形变范围内计算CoVTe和FeVTe的电子结构. 计算分析表明,晶格均匀形变△a/a0分别在-7% — +7%和-4.8% — +7%时,合金CoVTe和FeVTe仍然保持半金属性,而且它们的晶胞总磁矩分别稳定于2.00 μB和1.00 μB. 对于晶格均匀体形变而言,half-Heusler合金CoVTe和FeVTe具有较好的半金属性和磁性的稳定性.

