超临界CO2在岩石孔隙内流动状态的分子模拟

高 腾，赵伶玲，李偲宇

(东南大学 能源与环境学院，南京 210096)

1 引 言

深部储层的超临界CO2(温度高于304 K且压强高于73.8 atm)泄露是地质碳封存的主要风险. 当泄漏发生时，由于岩石孔隙尺寸、温度及压强的影响，超临界CO2在岩石孔隙中存在复杂的密度分布和流动特性[1-3]. 因此，研究超临界CO2在岩石纳米孔隙中的密度分布和流动特性，可以提高对岩石纳米孔隙中超临界CO2流动特性的认识.

目前，国内外学者通过分子模拟的方法对纳米孔隙内不同物质的流动过程进行了广泛研究，取得了丰硕的成果. Ghorbanian等[4]通过分子模拟的方法研究了纳米流动过程中，孔隙尺寸对H2O分子密度分布、流动速度及动力粘度的影响. Markesteijn等[5]采用分子模拟研究了压力驱动流动时，不同力场参数及温度对H2O分子流动速度的影响，验证了可以更加准确描述H2O分子纳米流动的力场模型. Wang等[6]通过分子模拟的方法分析了超临界辛烷在纳米级岩石孔隙内的流动速度分布，发现温度和孔隙尺寸均会对超临界辛烷的流动速度产生影响. Jiang等[7]采用分子模拟的方法研究了孔隙大小对超临界甲烷在硅纳米通道内流动过程的影响，分析了甲烷分子在岩石孔隙内的密度分布和流动状态. 然而，对岩石纳米孔隙中超临界CO2流动状态的研究却罕见报道.

本文采用分子动力学(MD)模拟的方法，选取镁橄榄石(Mg2SiO4)晶体块为固体相，构建了Mg2SiO4-CO2-Mg2SiO4的模拟系统，分析比较了地质封存条件下，孔隙尺寸(<37 nm)、温度(350 K-400 K)、压强(200 atm-300 atm)对超临界CO2在岩石孔隙内流动特性的影响，为指导岩石孔隙内超临界CO2泄漏提供理论指导.

2 分子模拟方法

本文采用分子模拟的方法，在计算中考虑了分子间的非键结作用及分子内的键结作用. 分子间的非键结作用包括范德华力和库仑静电力，范德华力采用L-J势能函数描述，库仑静电力采用库仑定律描述；分子内的键结作用包括键拉伸和键角弯曲，均采用谐波势能函数进行模拟. 模拟中Mg2SiO4和CO2分别选择CLAYFF[8]和EPM2力场模型[9]进行描述，示于表1.

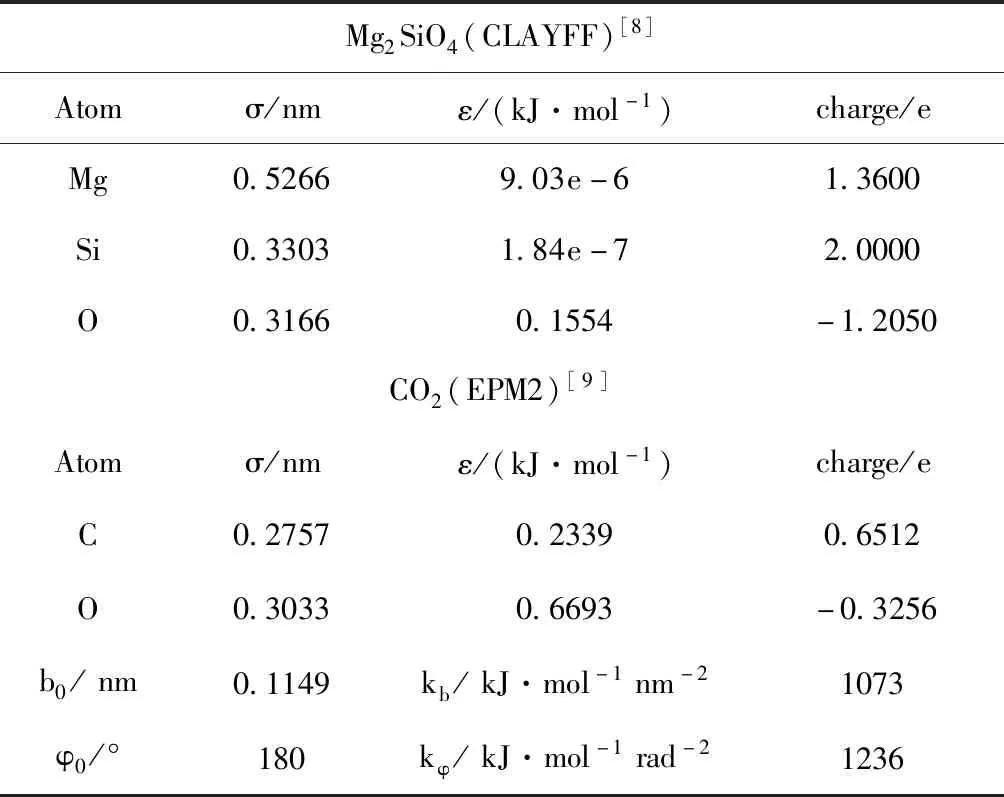
表1 Mg2SiO4和CO2力场

注：ε代表L-J势能曲线中的势能阱深度，nm；σ代表势能为零时，两点间的距离，nm.

计算选取Mg2SiO4晶体块为固体相，构建了如图1所示的Mg2SiO4-CO2-Mg2SiO4的模拟系统. Mg2SiO4晶体块沿Y方向的厚度为5 nm，系统在X和Z方向采用三维周期性边界条件，范德华作用截距设为1.2 nm. 分子模拟所采用的软件为LAMMPS[10]，模拟采用Leap-Frog算法，以1 fs的时间步长进行求解.

本文首先采用NPT系综进行5 nm的平衡模拟，使系统的密度和结构保持稳定. 在平衡模拟中，温度及压强的耦合分别采用基于Berendsen耦合器的velocity rescaling方法[11]和semi-isotropic方法[12]. 系统平衡后，采用NVT系综进行30 ns的非平衡模拟. 在非平衡动力学模拟中，沿+Z方向对每个原子施加一定大小的的体积力，推动流体流动[13].

图1 超临界CO2在岩石孔隙内的流动示意图Fig. 1 Schematic diagram of the flow of supercritical CO2

3 模拟结果与讨论

3.1 模型验证

本文首先对镁橄榄石的晶体结构进行研究，计算了350 K和200 atm条件下Mg-O、Si-O原子对的径向分布函数(RDF)，示于图2. 如图所示，Mg-O、Si-O的RDF曲线第一峰的位置对应了Mg-O、Si-O键的键长，Mg-O、Si-O原子对的第一峰分别位于r=2.01 Å、r=1.59 Å位置，这与Kudoh等[14]人在实验中得到的Mg-O(r=2.09 Å)、Si-O(r=1.63 Å)原子对的键长较为符合.

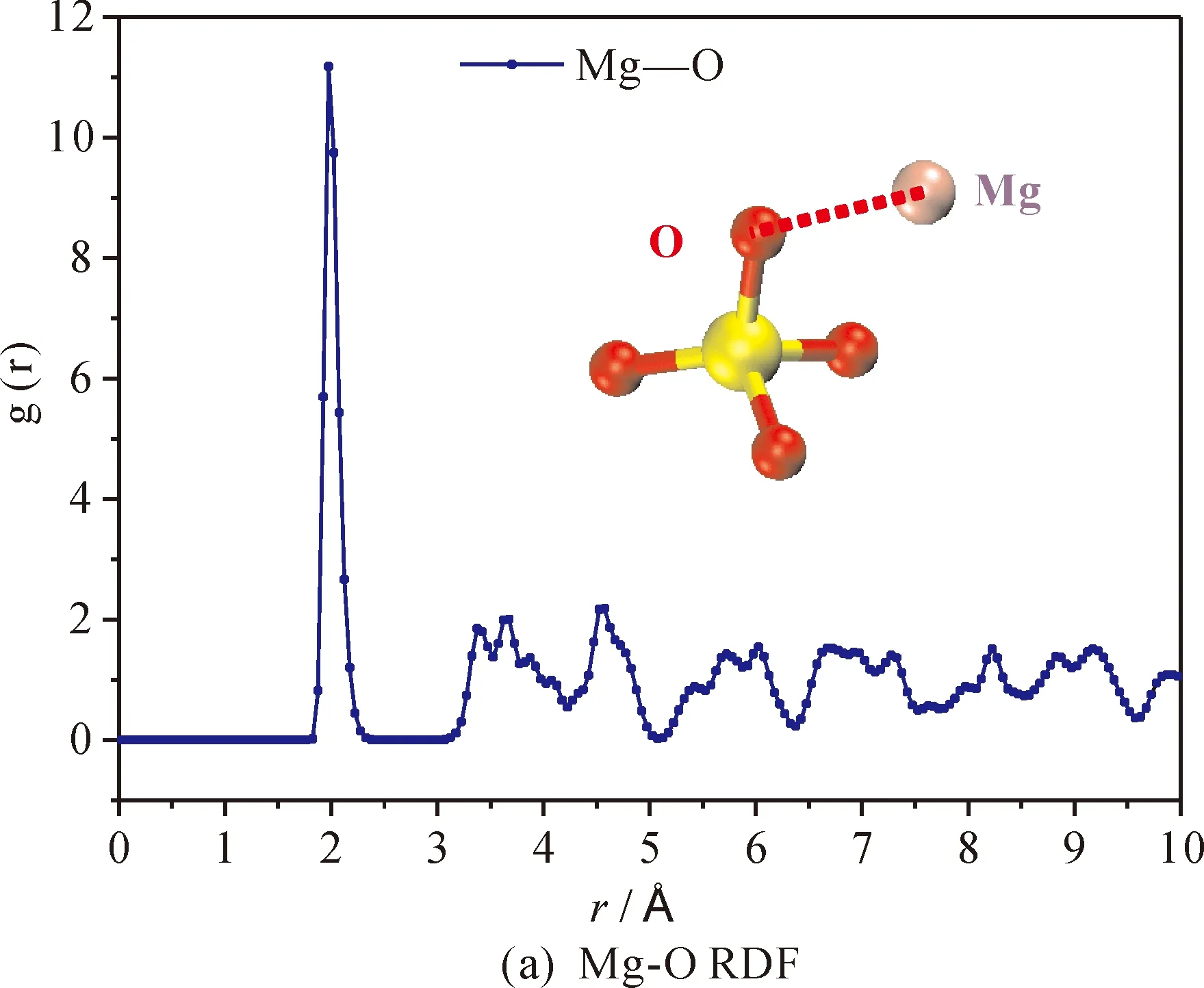
图2 350 K、200 atm条件下Mg2SiO4中Mg-O、Si-O原子对的RDF曲线Fig. 2 RDF of Mg-O and Si-O in Mg2SiO4 under 350 K and 200 atm

本文接下来对镁橄榄石(Mg2SiO4)晶体块进行了拉伸模拟，晶体块受到拉力并随着时间的推移沿受力方向发生形变，最终使Mg2SiO4晶体块的长度达到初始长度的1.2倍. 经数据分析，计算得到Mg2SiO4晶体块拉伸过程的应力-应变(σ-ε)曲线，示于图3. 从图中可以看出，Mg2SiO4先后经历了弹性形变(ε≤0.05)、塑性形变(0.05<ε≤0.125)和断裂(ε>0.125)三个阶段. 在弹性形变阶段，Mg2SiO4所受应力(σ)与其应变(ε)基本成正比. 通过拟合计算，此阶段中应力与应变的比值(即弹性模量)近似为293 GPa，较好地符合Liu等[15]人在实验中测得的弹性模量(约为287 GPa).

此外，应用所建CO2分子的模型和力场，计算得到不同温度条件下CO2分子的密度变化，示于图4. 从该图可以看出，CO2的密度随温度的升高而降低，模拟结果与美国标准与技术研究所(NIST)[16]提供的实验数据[17]吻合较好，进一步验证了本文所建立的计算模型和力场具有一定的可靠性和准确性.

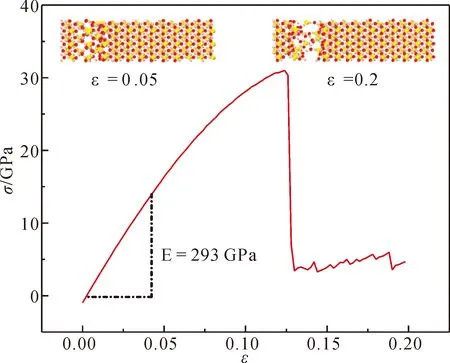
图3 Mg2SiO4的应力-应变曲线Fig. 3 Stress-strain curve of Mg2SiO4

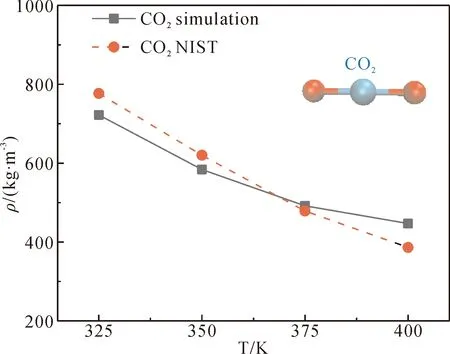
图4 超临界CO2密度随温度的变化Fig. 4 Densities of CO2 under diffferent temperatures

3.2 孔隙尺寸的影响

3.2.1孔隙尺寸对速度的影响

本文首先比较了超临界CO2在不同大小岩石孔隙内的速度分布，示于图5. 该图以孔隙中间位置为0点.

从图中可以看出，当孔隙尺寸H大于5 nm时，超临界CO2的速度曲线呈“抛物线”状，符合Poiseuille流动的运动规律，即由岩石表面至孔隙中心，CO2分子受到岩石表面分子的吸引力逐渐减小，阻碍CO2运动的作用力由壁面到中心逐渐减小，呈现出壁面速度低而中心速度高的分布特征. 当孔隙尺寸H小于5 nm时，超临界CO2分子的速度在岩石孔隙内无明显的“抛物线”状，类似于平推流. 这与Botan等[18]研究的水在不同孔隙尺寸的粘土纳米通道内的流动规律相符. 当孔隙尺寸H小于5 nm时，岩石壁面与CO2分子间的相互作用会强化CO2分子间的相互作用力，从而导致CO2分子以类似平推流的流动速度运动，而当孔隙尺寸H大于5 nm时，在远离壁面的CO2分子间的相互作用较弱，使得孔隙中间区域的超临界CO2分子可以在岩石孔隙内呈Poiseuille流动.

图5 不同孔隙尺寸下超临界CO2的速度分布Fig.5 Velocities of supercritical CO2 under different pore sizes

3.2.2孔隙尺寸对密度的影响

超临界CO2分子的平均密度随孔隙尺寸的变化，示于图6. 从图中可以看出，当孔隙尺寸H小于15 nm时，超临界CO2的平均密度随孔隙的减小而增大；而当孔隙尺寸H大于15 nm时，超临界CO2的平均密度不再受孔隙尺寸的影响，趋于620 kg/m3，这也与美国标准与技术研究所(NIST)提供的实验数据吻合较好.

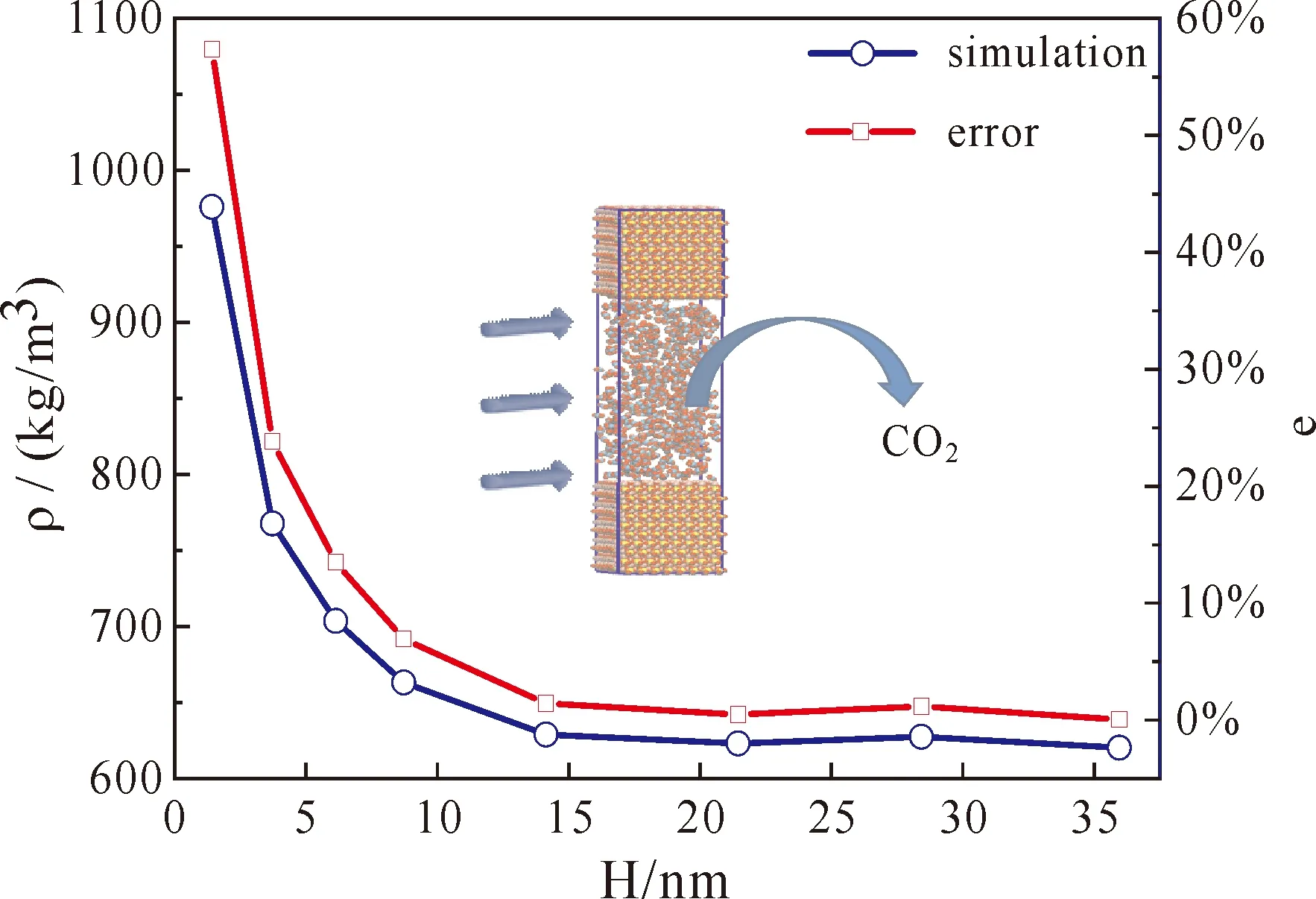
图6 不同孔隙尺寸下超临界CO2的平均密度Fig.6 Average density of supercritical CO2 under different pore sizes

为分析这种现象产生的原因，本文比较了孔隙尺寸H为7 nm和15 nm时，超临界CO2分子在岩石孔隙内的密度分布，示于图7. 该图以孔隙中间位置为0点. 从图中可以看出，在镁橄榄石的近壁面处，超临界CO2分子的密度分布呈震荡状态，有两个明显的峰，这主要是因为镁橄榄石表面与超临界CO2分子间具有强烈的相互作用，使CO2分子在镁橄榄石近壁面形成一种“类固体”[19]，具有较高的密度，这与Ghorbanian等[20]人发现的单相H2O分子在碳纳米管中的密度分布规律相似.

进一步的分析发现：在不同大小的岩石孔隙内均发现了密度震荡，近壁面处的密度震荡现象并不会随岩石孔隙尺寸的增大或减小而消失；同时，密度震荡的距离L并不受孔隙尺寸大小的影响，在不同大小的岩石孔隙内，密度震荡的距离均持续到距离岩石表面L=1.5 nm处.

因此，在孔隙尺寸H小于15 nm时，孔隙尺寸越小，近壁面处密度震荡的影响作用越明显，孔隙内超临界CO2分子的平均密度越大. 虽然随着孔隙尺寸的不断增大，近壁面处的密度震荡现象依然存在，但是由于其震荡距离L保持不变，其对超临界CO2平均密度的影响不断减小，最终使得孔隙尺寸H大于15 nm时，密度震荡对超临界CO2平均密度的影响不再重要.

3.3 温度和压强的影响

3.3.1温度和压强对速度的影响

考虑到孔隙尺寸H小于15 nm时，密度震荡现象的影响，本文选取孔隙尺寸H为15nm，研究不同温度和压强下超临界CO2在镁橄榄石表面的速度分布，示于图8.

图7 不同孔隙尺寸下超临界CO2的密度分布Fig.7 Density profile of supercritical CO2 under different pore sizes

图8 不同温度和压强下超临界CO2的速度变化Fig.8 Velocity profile of supercritical CO2 under different temperatures and pressures

从图中可以看出，随着温度的升高和压强的降低，岩石孔隙内超临界CO2分子的速度逐渐增加，其速度曲线仍然呈“抛物线”状，但是速度分布的“抛物线”曲率却呈现出不同. 这种行为在宏观上反映为流体的动力粘度变化，即随着温度的升高，CO2分子的流动速度不断增加，动力粘度不断减小；随着压强升高，CO2的流动速度不断减小，动力粘度却不断增加. 而Bao等[21]人发现：H2O在纳米孔隙中的动力粘度随温度的升高而增加，却不受压强直接影响.

因此，超临界CO2在镁橄榄石孔隙内流动时，采用降低温度、增加压强的方法可以减弱镁橄榄石表面对CO2分子的吸引力，使得CO2分子的流动速度降低，防止超临界CO2的泄漏.

3.3.2温度和压强对密度的影响

孔隙尺寸H为15 nm时，不同温度和压强下超临界CO2在镁橄榄石表面的密度分布，示于图9. 从图中可以看出，不同温度和压强条件下，超临界CO2分子在镁橄榄石表面的密度震荡依然存在，而且两个峰的峰值对应的位置不受温度和压强的影响. 其中，第一个峰的峰值相对较大，决定于岩石表面与超临界CO2分子间的相互作用力，受温度和压强影响影响较大. 随温度的升高而降低，随压强的增大而增加，即增大压强可导致镁橄榄石表面对超临界CO2分子的吸引力增强，而升高温度反而会减弱这种吸引力，增加CO2分子的流动速度.

图9 不同温度和压强下近壁面处超临界CO2的密度分布Fig.9 Density profile of supercritical CO2 near the surface under different temperatures and pressures

4 结 论

本文采用非平衡动力学模拟的方法研究了超临界CO2在岩石孔隙内的流动特性，分析了孔隙大小、温度及压强对CO2流动特性的影响，得到以下结论.

(1) 超临界CO2在岩石孔隙内流动时，当岩石孔隙小于5.0 nm时，速度分布呈平推流的运动规律，只有当岩石孔隙大于5.0 nm时，超临界CO2分子在岩石孔隙内的流动才符合Poiseuille流动的运动规律.

(2) 超临界CO2在岩石近壁面处具有较大的分子密度，呈现一种密度震荡现象，单侧壁面的震荡距离在1.5 nm左右，不受孔隙尺寸大小的影响，当岩石孔隙小于15 nm时，这种密度震荡就会显著影响超临界CO2在岩石孔隙内的平均密度.

(3)岩石壁面处CO2分子的密度震荡受温度和压强的影响，采用降低温度和增大降低压强的方法，可以使得密度震荡的第一峰值增大，造成岩石表面对CO2分子的吸引力增强，减小CO2分子的流动速度.