基于PSO-BP 神经网络模型的IGBT 老化预测

边少聪，王 宇

（西安工程大学 电子信息学院，西安 710048）

0 引言

随着IGBT（绝缘栅双极型晶体管）性能的不断提升，其应用范围不断拓宽，可靠性愈发重要。正常工况下，IGBT 会因开关损耗和通态损耗等产生的热量使得器件温升，在长期运行中产生疲劳失效累积，使IGBT 模块不断老化，从而降低器件乃至整个系统的可靠性。因此，有必要对IGBT 的老化进行预测[1]。

由于正常运行过程中IGBT 的老化过程缓慢且老化数据不易获取，当前对于IGBT 老化及剩余寿命的研究主要是通过加速老化试验来模拟正常老化的过程[2]。在功率循环和温度循环的加速老化实验条件下，分别构建解析模型和物理模型，以探究IGBT 失效循环次数与结温[3-4]、应力、应变的关系，从而对IGBT 的可靠性作出评估。

为了更好地实时监测IGBT 模块的老化状态，采集老化过程中IGBT 的失效电气参数，并结合梯度下降、SVM（支持向量机）、BP 神经网络等机器学习算法，构建IGBT 的老化失效模型。当使用模型预测到失效参数接近失效标准时，就能及时检修更换IGBT，故这种模型也被称为基于数据驱动的解析模型[5]。本文基于IGBT 加速老化试验数据，利用这种方法来建立IGBT 模块的老化预测模型。

1 实验数据提取及预处理

本文的实验数据来源于NASA PCoE 研究中心公开的IGBT 加速老化数据，该数据包含4 种实验条件下的IGBT 加速老化数据。本文选取其中在IGBT 栅-射极施加方波电压下的加速老化试验数据。实验选用IR 公司生产的型号为IRG4BC30K 的IGBT 器件。从IGBT 开始老化到老化结束，共对其进行418 次IGBT 瞬态测量。每组测量包括施加在门极-发射极之间的PWM（脉冲宽度调制）方波信号和与之对应的集射极电压信号，每个信号有100 000 个采样点。图1 和图2所示为第9 组瞬态测量值。当施加在IGBT 门极-发射极之间的方波信号从10 V 开始减小到0 V时，IGBT 处于动态关断过程，并在此过程中集射极电压会产生关断电压尖峰。

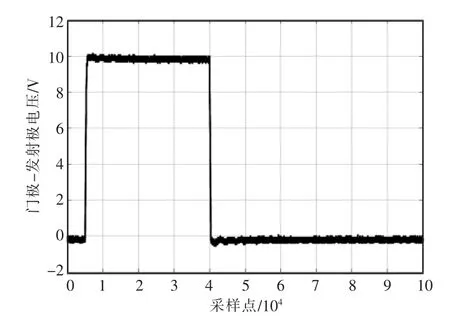
图1 第9 组测量值的门极-发射极电压

提取418 组瞬态测量数据的集射极关断电压尖峰值，并绘制图3 所示的集射极瞬态关断电压峰值退化曲线。由图3 可知，随着IGBT 的老化，IGBT 集射极关断电压峰值呈逐渐减小的趋势，因此可将其作为检测IGBT 老化过程的失效参数。

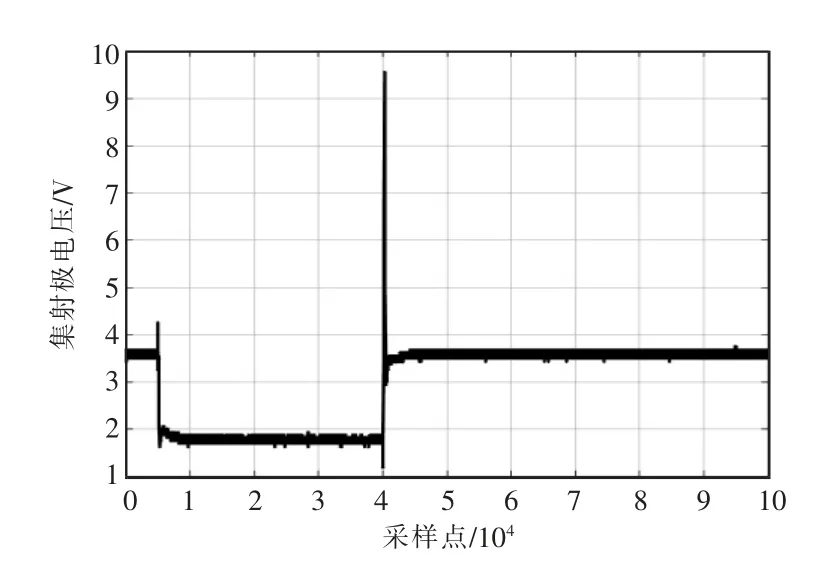
图2 第9 组测量值的集射极电压

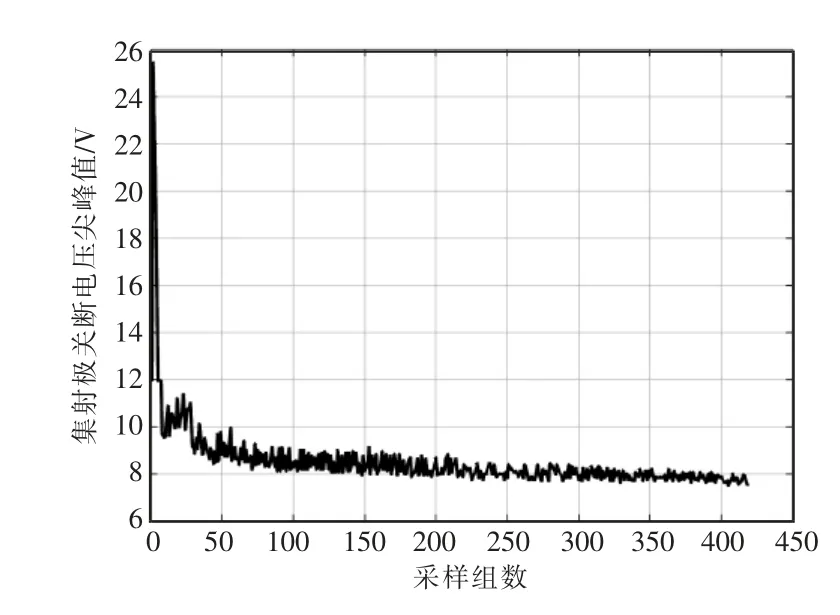
图3 IGBT 集射极关断电压峰值退化曲线

通过对图3 中每组关断电压尖峰值的对比可知，虽然集射极关断电压尖峰值随着老化进程整体呈现递减趋势，但相邻采样组之间的数据波动性较大。使用卡尔曼滤波对其进行平滑处理，并将处理结果作为试验数据。其中卡尔曼滤波中的过程噪声方差和测量噪声方差的初始值分别设置为0.9 和10。因为卡尔曼滤波的初始值是从0 开始变化的，为了解决初始点滤波与原始数据相差较大的问题，用实验原始数据的初始9 个数据点替代卡尔曼滤波的初始9 个点。对数据进行平滑处理的结果如图4 所示。通过与图3 对比发现，经卡尔曼滤波后，集射极关断电压尖峰值下降趋势比平滑前更明显。

通过分析可知，实验数据并非为线性降低，且呈现一定的波动性。而且作为老化预测模型，需要算法具有一定的泛化能力。因此本文针对失效参数的数据特点选择非线性逼近能力强的BP 神经网络作为训练算法，建立IGBT 老化失效模型。

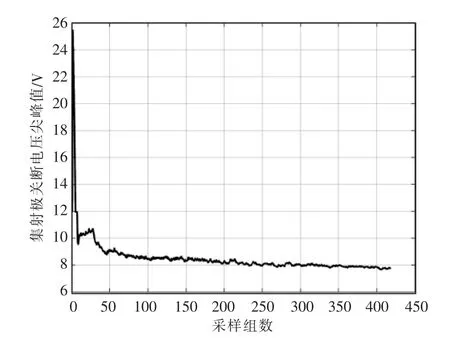
图4 卡尔曼滤波处理后的IGBT 集射极关断电压峰值退化曲线

从BP 神经网络算法原理上看，网络权值的调整是沿着局部改善的方向进行的，易使网络收敛到局部极小值，从而导致误差增大。这与网络的初始权值、阈值密切相关，为此，本文先引入GA（遗传算法）对网络的初始权值、阈值进行优化。而GA 在寻优过程中进行的交叉和变异操作可能会破坏其中最优的初始权值、阈值信息，使得算法收敛性能降低[6]。因此，本文引入PSO（粒子群优化）算法对BP 神经网络的初始权值、阈值进行优化，以弥补GA 的不足。最终将优化后的初始权值、阈值带入BP 神经网络进行训练，从而避免因初值选取而使BP 神经网络陷入局部最优，提高了模型的准确度。

2 BP 神经网络及其优化预测模型

2.1 BP 神经网络的建模测试过程

为了充分利用老化过程中的失效参数，建立更加精准和更具实际应用价值的IGBT 老化预测模型，本文在建模过程中使用迭代的思想，即用上一步输出数据的期望值作为下一步数据预测的输入数据。对获取418 组失效参数进行处理，以8 个数据为单位，将第1—8 个数据作为BP 神经网络模型的输入数据，将第9 个数据作为与之对应的期望输出数据；然后以第2—9 个数据作为BP 神经网络模型的输入数据，将第10 个数据作为与之对应的期望输出数据；以此类推，共得到410 组样本集，如表1 所示。

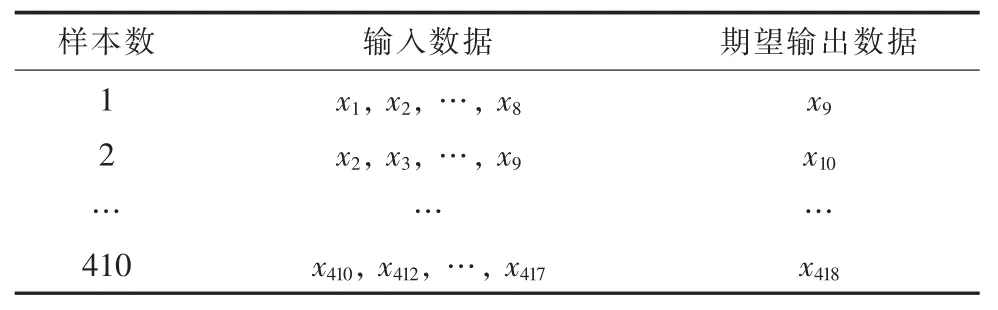
表1 BP 神经网络样本数据划分

将上述410 组样本集随机划分为370 组和40 组样本数据。370 组样本数据作为训练集用于BP 神经网络的训练；40 组样本数据作为测试集，来对训练好的BP 神经网络进行验证和评估。

BP 神经网络结构如图5 所示，图中x1—x8为输入，y1为输出，ωij为输入层与隐含层之间的链接权值，ωjk为隐含层与输出层之间的链接权值。

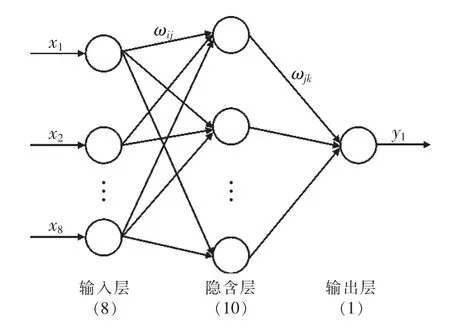
图5 BP 神经网络结构

首先，根据IGBT 老化预测模型的输入数据确定网络的输入层神经元个数为8，其含义为老化失效参数的8 维历史信息；根据期望输出数据确定网络的输出层神经元个数为1，其含义为以这8 维老化历史信息作为输入数据预测的下一维老化失效参数。根据多次训练调试，最终以在测试集上的预测误差最小为原则，选择隐含层神经元个数为10。

其次，初始化输入层与隐含层、隐含层与输出层之间的链接权值ωij和ωjk，隐含层和输出层的阈值；选择隐含层和输出层的传递函数[7]。

最后，使用训练集对网络进行训练，直至满足误差要求，从而建立IGBT 老化预测模型；结合测试集对模型进行验证评估。

2.2 GA-BP 神经网络的建模测试过程

GA 是指将需要优化的参数进行染色体编码，并确定合适的适应度函数，以计算适应度的值。在迭代的过程中，不断删除适应度差的编码，保留好的适应度值对应的编码，同时产生新的编码，直至最终寻找到最优值。

图6 为GA-BP 神经网络算法流程。

首先，根据神经网络的拓扑确定需要优化参数的个数并按一定顺序进行编码[8]，以方便优化后的参数解码。GA-BP 中需优化的参数包括连接权值及阈值。

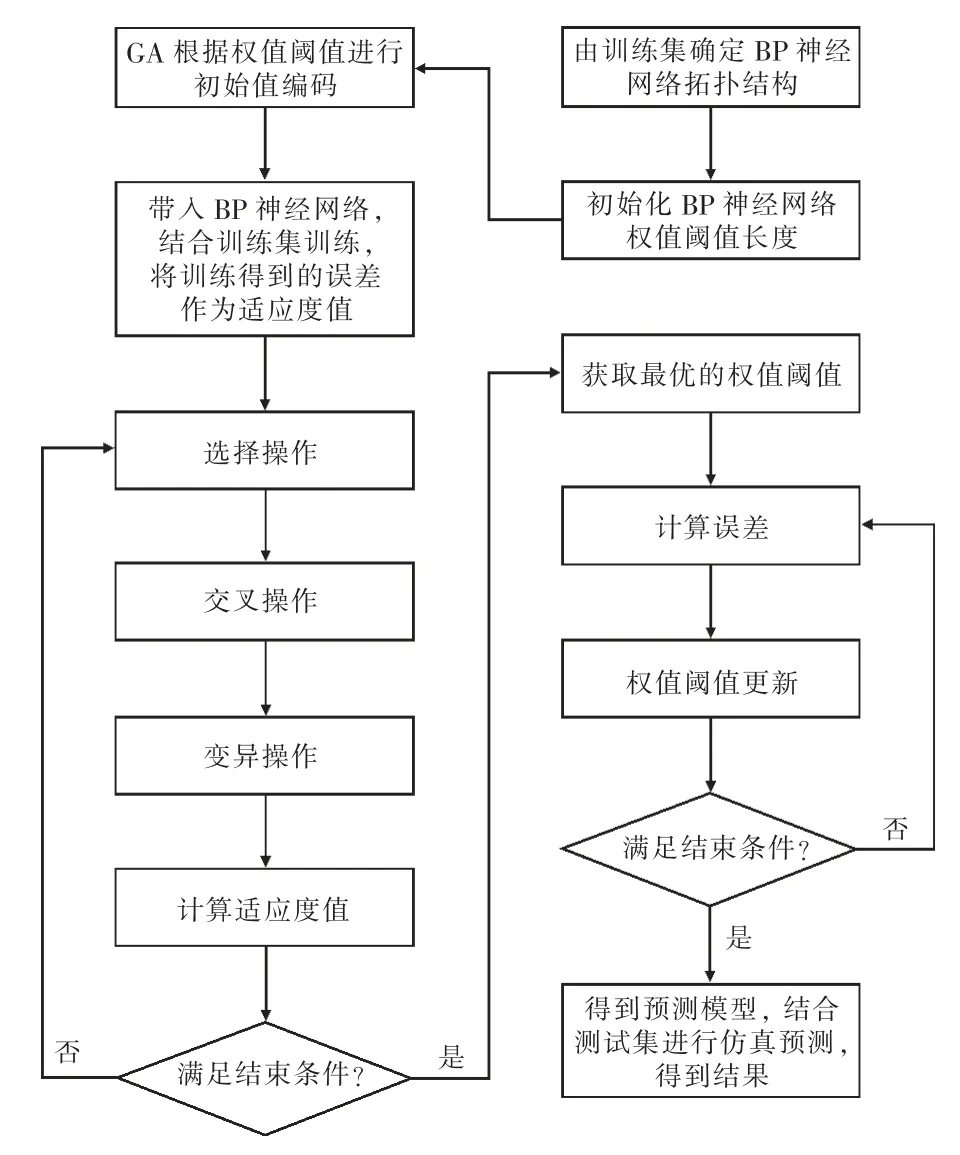
图6 GA-BP 神经网络算法流程

其次，将个体解码后作为BP 神经网络的初始权值、阈值并结合训练集进行训练，得到训练集的预测值，并计算适应度函数值[9]：

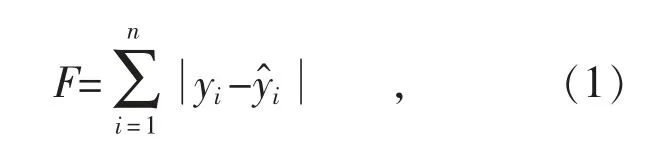
式中：n 为训练集数据个数；yi为训练集期望输出值；为训练集数据的拟合值。此时适应度值越小越好。

然后，根据适应度值对个体进行选择，保留优秀编码，舍去不良编码。在此基础上进行交叉和变异操作，产生新的个体以进行下一步适应度值的计算。如此反复迭代直至满足条件。

最后，将最优的个体解码作为寻优后的BP神经网络的初始权值、阈值，将其带入BP 神经网络并结合训练集进行训练，从而得到IGBT 老化预测模型，并结合测试数据对其进行验证评估。

2.3 PSO-BP 神经网络的建模测试过程

PSO 中每个粒子维度代表需要优化参数个数，参数的大小用粒子的位置来描述。以式（1）作为适应度函数计算粒子的适应度值进而确定粒子的好坏，并以此来计算粒子更新速度，其大小决定了粒子位置改变的方向和大小。通过不断计算适应度值来修改粒子位置，从而获得最优粒子。

图7 为PSO-BP 神经网络算法流程。

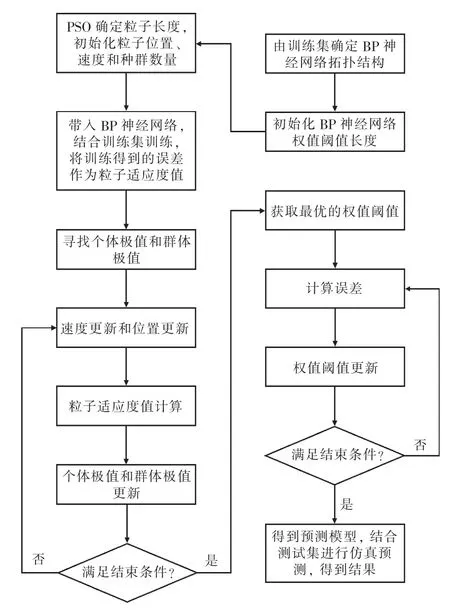
图7 PSO-BP 神经网络算法流程

首先，根据BP 神经网络需优化的初始权值阈个数确定粒子维度，在确定位置和速度的范围后，随机初始化群体中每个粒子的位置和速度[10]。

其次，以粒子作为初始权值、阈值带入BP神经网络结合训练集训练后的训练集预测误差作为适应度的值，并记录群体极值和个体极值，同时用个体最优位置Pp和群体最优位置Pg分别记录个体极值和群体极值所对应粒子位置。

然后，据式（2）和式（3）计算粒子速度并更新粒子位置，判断其是否超出设置范围，超出则以边界值代替[11]。将其带入网络，获取训练集的预测结果后带入式（1）。重新计算适应度值后，更新个体极值与群体极值，并记录新的极值所对应的粒子位置[12]。如此迭代直至满足要求。

式（2）—（4）中：Vi，k和Xi，k表示第k 次循中第i 个粒子的速度和位置；r1和r2为0～1 之间的随机数；c1和c2为非负常数，称为加速因子[13]；X，V，Pp，Pg均为1 行d 列的向量；d 为需要寻优参数的个数；w（k）为线性递减惯性权重；Imax为最大迭代次数；ws为初始惯性权重；we为最终惯性权重。ws＞we，从而在计算速度时，随着迭代的进行，w（k）越来越小，使算法在迭代初期具有较强的全局搜索能力，而在迭代后期具有较强的局部搜索能力[14]。

最后，将寻优后的最优粒子位置作为优化的BP 神经网络初始权值、阈值。将其解码后带入BP 神经网络结合训练集进行训练，以得到IGBT老化预测模型，并用测试集对其进行验证评估。

3 试验结果与误差分析

3.1 BP 神经网络试验结果及预测误差

将样本集随机划分为训练集和测试集后，对样本进行归一化处理，以消除数据间的数量级差别，从而减小预测误差。根据上文所述设置BP 神经网络的输入-隐层-输出神经元个数为8-10-1，隐含层和输出层的传递函数分别为logsig 和purelin，最大迭代次数为500 次，训练精度为10-5，学习速率为0.001。

在MATLAB 中调用newff 函数生成的BP 神经网络后，因为网络的初始权值、阈值未经优化，故没有设置初始权值、阈值。而在调用train 函数训练网络时，算法会随机赋予BP 神经网络初始权值、阈值，这样会使每次训练好的网络在测试集上表现出不同的误差，且误差波动范围较大。因此，本文通过多次训练得到不同的训练好的BP 神经网络，带入测试集进行预测评估，以预测误差最小为原则，得到表现最好的BP 神经网络模型。预测结果和预测误差如图8 和图9 所示。

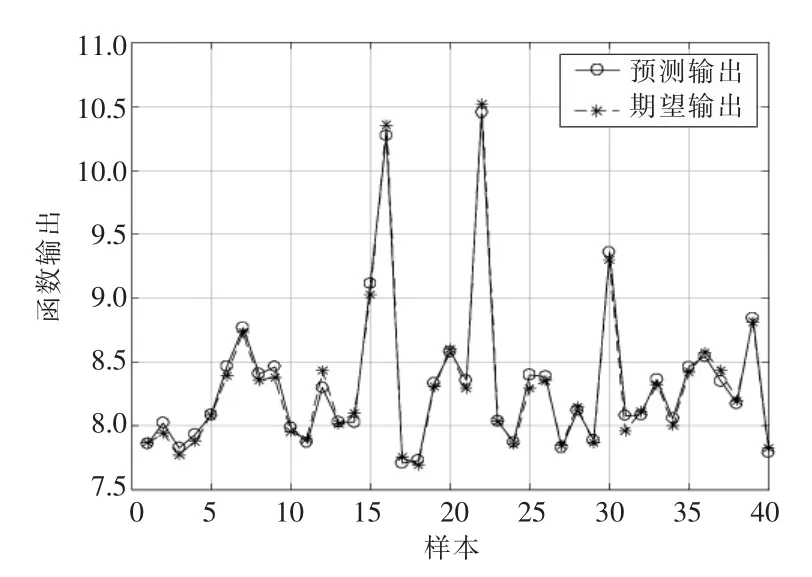
图8 BP 神经网络预测结果

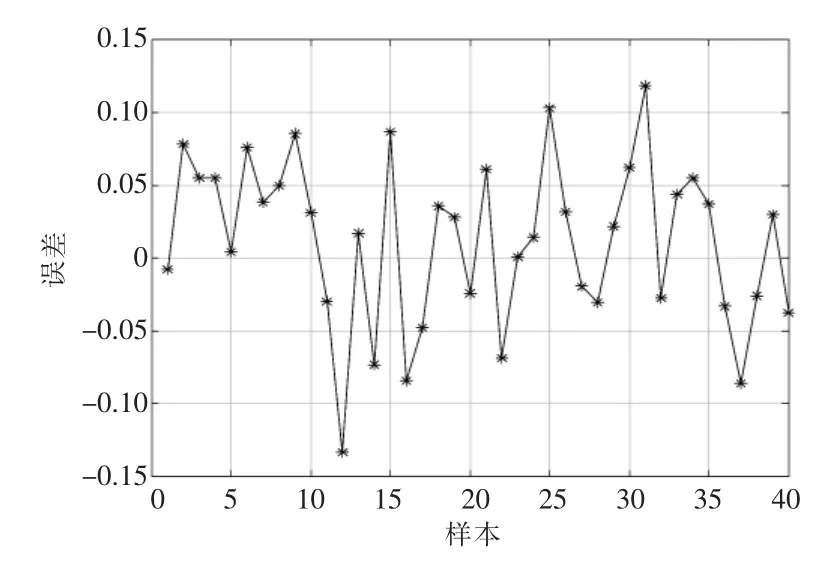
图9 BP 神经网络预测误差

3.2 GA-BP 神经网络试验结果及预测误差

由上文所述可知，由于BP 神经网络初始权值、阈值的选取问题，可能会使网络在训练过程中陷入局部最优，造成每次训练好的BP 神经网络在测试集上的误差波动较大。为解决此问题，本文使用GA 对BP 神经网络的初始权值、阈值进行优化。

将BP 神经网络的初始权值、阈值按输入层-隐含层的链接权值、隐含层神经元阈值、隐含层-输出层链接权值及输出层神经元阈值的顺序作为编码顺序。本文BP 神经网络的输出-隐含-输入层结构为8-10-1，故所需要优化的参数的个数为8×10+10+10×1+1=101。在GA 中以此编码顺序进行实数编码[15]，创建的每个个体为101 维的向量，向量中的每个数编码的值为－2～2。设定群体数为30，迭代次数为100。

GA 的输入为这30 组个体编码值，将个体进行解码后结合训练集进行训练，得到训练集的拟合值，按照式（1）计算适应度函数的值，并以其最小作为寻优目标。通过对个体进行的选择交叉和变异操作，使寻优目标在迭代过程中不断减小。最终经100 次迭代后得到的适应度函数最小个体即为寻优目标，也就是GA 的输出。

将GA 寻优后的初始权值、阈值带入BP 神经网络，结合训练集进行多次训练后，分别带入测试集进行预测评估，以预测误差最小为原则，得到表现最好的GA-BP 神经网络模型。预测结果和预测误差如图10 和图11 所示。

3.3 PSO-BP 神经网络试验结果及预测误差

虽然经GA 优化后的BP 神经网络在测试集上的预测误差波动和预测误差明显减小，但是GA 以一定概率进行的交叉和变异操作产生新个体时，这两种操作有可能破坏最优个体的编码信息。为解决此问题，本文使用PSO 算法对BP 神经网络的初始权值、阈值进行优化。

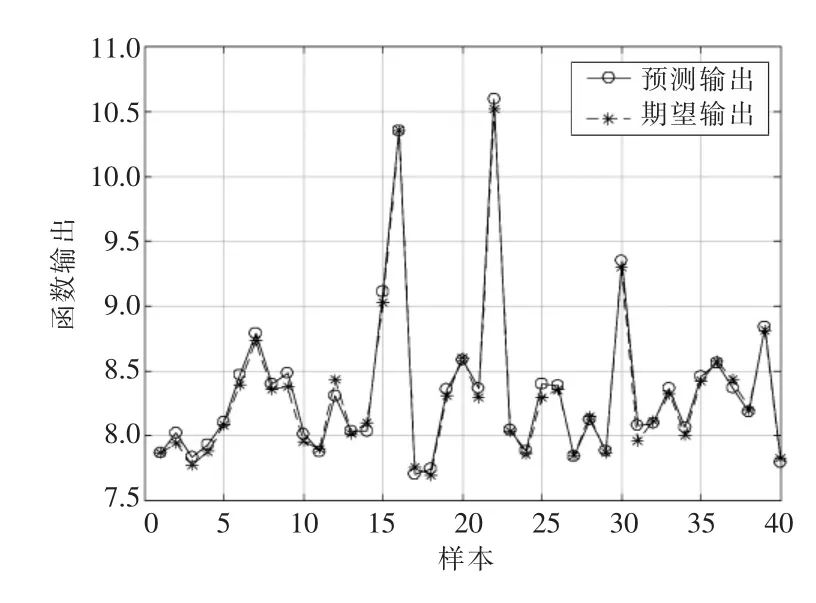
图10 GA-BP 神经网络预测结果

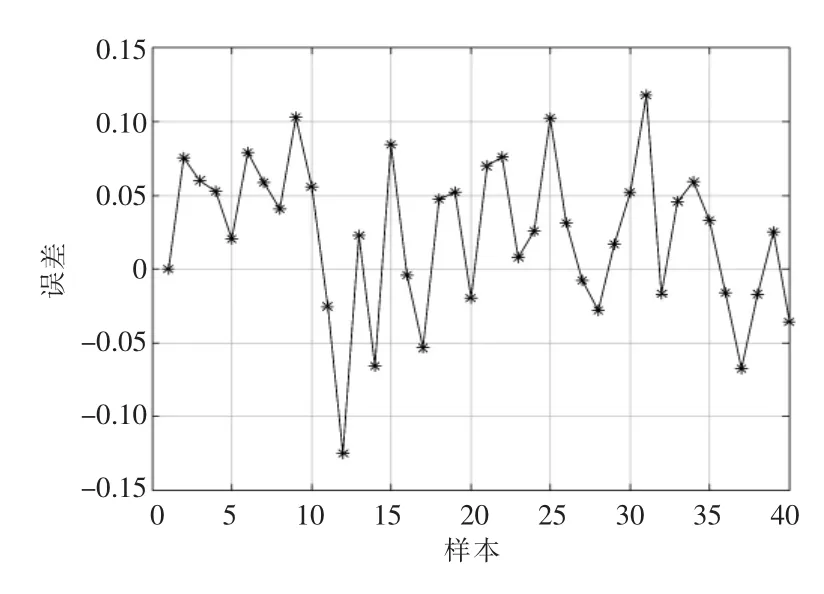
图11 GA-BP 神经网络预测误差

由上文分析可知，PSO 算法需对101 维BP神经网络的初始权值、阈值进行优化，故采用上文所述的编码顺序对101 位粒子进行实数编码。其中每个粒子的位置和速度的范围分别为－2～2和－0.5～0.5，代表初始权值、阈值的取值范围和变化范围。设置种群个数为30，即创建30 组不同的BP 神经网络初始权值、阈值，迭代次数为100。

PSO 算法的输入为这30 组不同的粒子，也就是30 组不同的BP 神经网络初始权值、阈值，结合训练集进行训练，得到训练集的拟合值，并按照式（1）计算适应度函数的值，即为训练集的训练误差，并以其最小作为寻优目标。计算粒子速度，更新粒子位置，使寻优目标在迭代过程中不断减小。30 组粒子均按照使目标函数最优的方向进行迭代，即在迭代过程中粒子追踪的是该粒子历史最优值和群体历史最优值[16]，所以并不会破坏最优粒子的编码，从而克服了GA 中可能会破坏最优个体编码的不足。最终经100 次迭代后输出的最优粒子的位置即群体最优位置Pg也就是PSO 算法的输出。

使用PSO 寻优后的初始权值、阈值带入BP神经网络结合训练集，经多次训练得到不同的训练好的BP 神经网络，带入测试集进行预测评估，以预测误差最小为原则，得到表现最好的GA-BP神经网络模型。预测结果和预测误差如图12 和图13 所示。

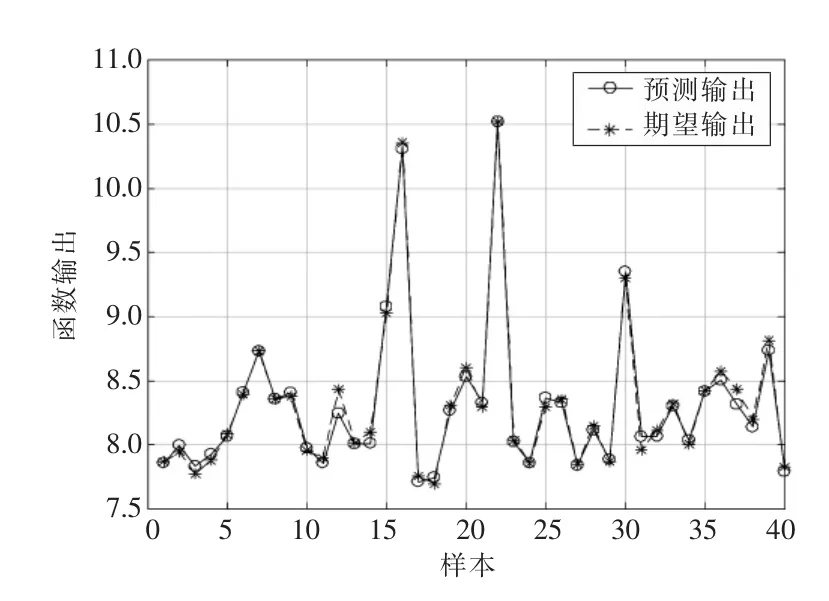
图12 PSO-BP 神经网络预测结果

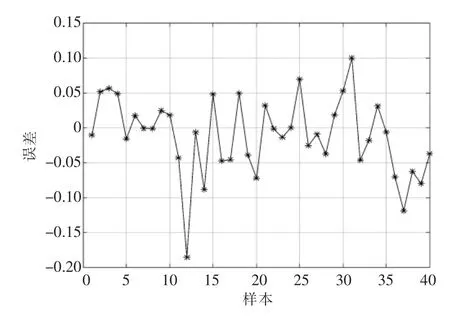
图13 PSO-BP 神经网络预测误差

3.4 误差分析

多次训练后获得的最优IGBT 退化模型中，经GA 和PSO 优化参数后的网络预测误差均低于BP 神经网络，且其中以PSO-BP 神经网络的预测误差最小。

为了更好地评价BP 神经网络、GA-BP 神经网络和PSO-BP 神经网络，应用训练集对3 种神经网络进行反复训练，并带入测试集进行预测评估，得到预测值的均方误差（EMS）、平均绝对误差（EMA）和相关系数（R2）的多次训练平均值（见表2），从而对BP神经网络、GA-BP神经网络、PSO-BP 神经网络进行对比分析，以评价网络的预测性能。计算公式为式（5）—（7）。其中，EMS和EMA的值越小越好；而R2的值越接近于1，预测数据与测试数据的相关性越高。

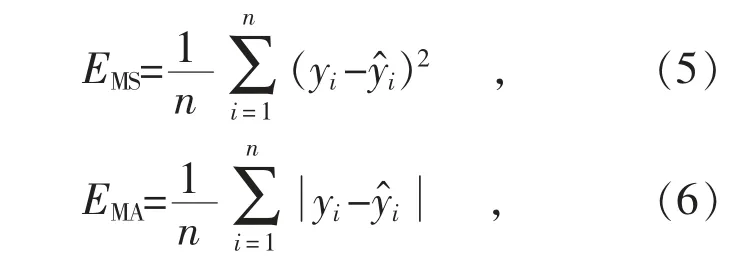
通过表2 数据可以看出：PSO-BP 神经网络的均方误差和平均绝对误差最小，且相关性最强；GA-BP 神经网络次之；不经优化的BP 神经网络取得的效果最差。据此可以得出结论：经GA 和PSO 算法优化后的网络均优于BP 神经网络，而且其中以PSO-BP 神经网络的性能最优。

表2 BP 神经网络、GA-BP 神经网络及PSO-BP 神经网络预测效果对比

4 结语

本文分别构建了基于BP 神经网络、GA-BP神经网络和PSO-BP 神经网络的IGBT 老化预测模型，并且以NASA PCoE 研究中心公开的IGBT加速老化数据为数据集，对模型进行验证并测试。通过对测试集预测值的误差对比分析可知，PSOBP 神经网络所建立的老化预测模型性能最优，GA-BP 神经网络次之，未经优化的BP 神经网络取得的效果最差。本文对老化实验中的退化参数建立退化模型，并通过GA 和PSO 算法对其进行优化，从而建立更精准的IGBT 老化预测模型。