浅谈线性规划在实际生活中的应用

曹亚群

（安徽水利水电职业技术学院，安徽合肥 231603）

1 什么是线性规划

线性规划是运筹学的重要分支，是合理分配及利用有限资源，以取得最佳经济效益的一种优化方法。它采取的是在一系列条件约束下，获得最优值的数学理论[1]。线性规划是一种数学规划方法，满足约束条件下，让目标函数取得最优值。它要解决的问题通常约束条件及目标函数是线性关系，约束条件是不等式或者等式，目标函数取极值。线性规划在管理学、建筑学、经济学等领域都有着广泛的应用，例如：下料问题、库存问题、运输问题等。线性规划都有一定的形式，标准形式如下：

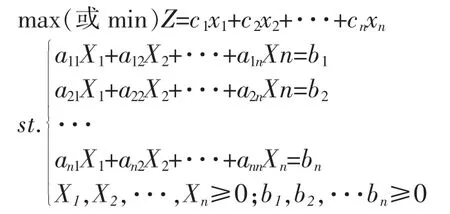
2 线性规划在实际生活中的应用

在我们的实际生活中，可以利用线性规划解决很多问题以减少人们的工作量、节约经费，提高工作效率[2]。生活中一些常见问题，比如两种不同型号材料的配比问题、话费选用套餐问题等，都可以用线性规划这种统筹方法找到最优解。下面，我们就以生活中某些常见问题为例，说明线性规划在实际生活中的应用。

2.1 线性规划在合理下料问题中的应用

合理下料问题是线性规划模型中的典型问题，建筑施工中，需要大量的各种各样的原材料，比如：钢材、木材、铝合金、砂、石、塑钢等建筑材料，而生产厂家只能提供一定规格的原材料，实际施工时要裁减才能得到所需要的规格，这样必然会产生残料，造成一定的损失和浪费，所以，合理下料，尽量减少产生残料，这让建筑企业能够减少成本投入，获得更高的经济效益[3]。下面，选用一个例子来说明线性规划在下料问题中的实际应用。

问题：要把20 根4 m 长和25 根5 m 长的同规格钢材，截成1.5 m 的50 根，1.2 m 的80 根，如何下料废料最少?(所有下料方法见表1)

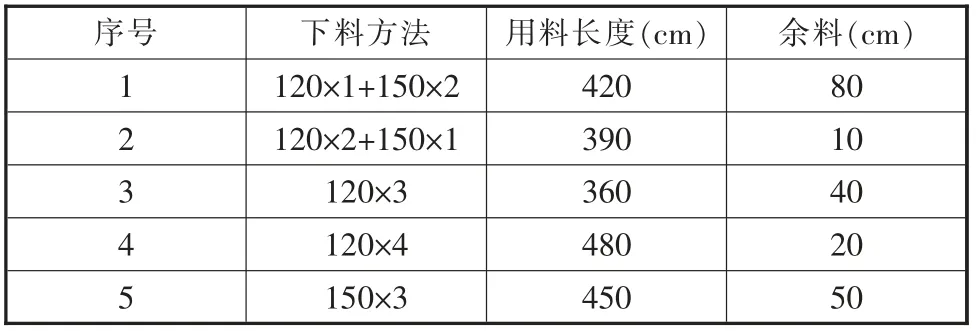
表1 下料方法

解：设用以上五种方法分别各用X1，X2，X3，X4，X5，次，则min f（X）=80X1+10X2+40X3+20X4+50X4

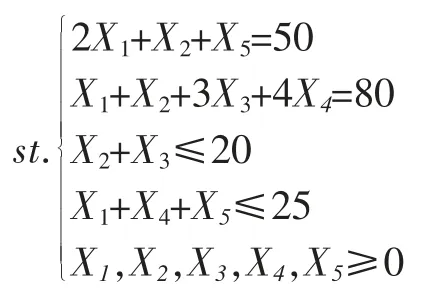
运用LIND0 软件，解得X1=0，X2=20，X3=0，X4=10，X5=10，即方法2 用20 次，方法4 用10 次，方法5 用10次，废料最少为900 cm。

2.2 线性规划在广告投放问题中的应用

如今，随着人民生活水平的不断提高，几乎每家都有电视，电视的普及率已经相当高了。尤其是目前手机、 电脑等电子产品的普及更是让人们感受到科技的力量。鉴于此，很多商家将目光投向了各种应用媒体平台的广告时段，目的就是增加自己的产品在人们视线中的出现频率。各个广告投资商需要根据具体情况，弄清楚各个媒体平台播放广告的时间及所需资金，以便获得更大的利润[4]。接下来我们用实际生活中的例子进行举例分析。

问题：某商家在投入资金不超过80 万元的条件下，需要保证至少有200 万女性观众观看广告，其中在电视台投入的广告费用不超过50 万元，电视台在白天至少播出3 次，在晚上至少播出2 次，无线电广播和杂志的广告播放次数均不低于5 次且不超过10 次,广告市场调查结果如表2 所示，问要想获得理想的广告效果应该如何安排播放次数。

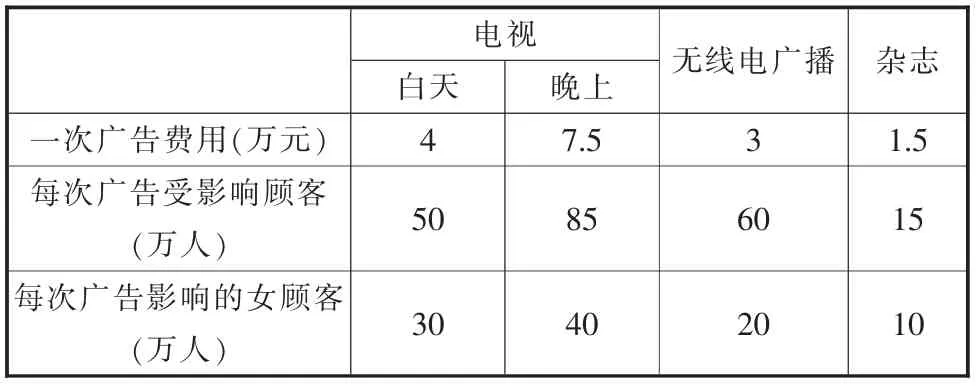
表2 广告市场调查结果

解：设电视台的广告在白天的播放次数为X1次，晚间的播放次数为X2，无线电广播播放X3次，杂志的广告刊登为X4次。则：

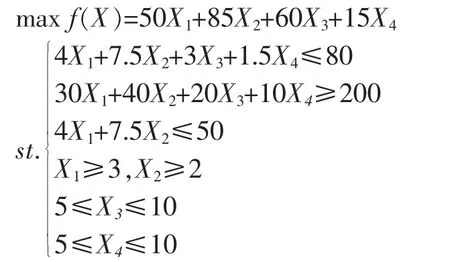
运用LIND0 软件，解得X1=3，X2=3，X3=10，X4=10，此时，总观看人数是1 155 万人，女性观看人数是510万人，总支出是79.5 万元。

2.3 在集合料问题中应用

解决集合料问题必须满足一定的条件，如种类、含量等，用数学语言表达各个条件，就是线性规划模型中的约束条件，要求所用的运输费用最省，用数学语言表达，就是线性规划模型中的目标函数，在集合料问题中，有很多不同方案被选择，优化目的就是从众多方案中选出一个最优方案[5]。

问题：某个筑路工地铺设道路基层，需要10 000 m3集合料，准备从两个弃土堆取混合料，已知弃土堆A 的材料成分为：砾石含量70%，砂含量30%，弃土堆B 的材料成分为：砾石含量30%，砂含量60%，粘土含量10%，集合料的成分含量要求为：砾石含量60%,砂含量50%，粘土含量8%。从弃土堆A 取料的装载运输费为2元/m3，从弃土堆B 取料的装载运输费为3.2 元/m3。问应如何取料才能使总的运输费用最少?

解：设从弃土堆A、B 取料数量分别为X1、X2m3，则：

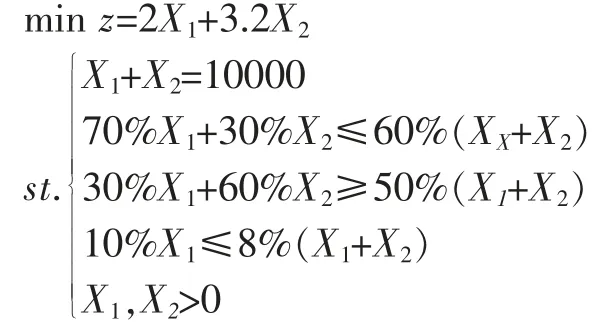
解得:X1=3 333 m3，X2=6 667 m3即从弃土堆A取料3 333 m3，从弃土堆B 取料6 667 m3，这样配料装卸运输费用最少为28 000 元。

3 结语

线性规划是有力的数学工具，它的重要目标就是规划出各种“最优”，即如何用最佳的方式分配有限的资源，以获得最佳经济效益，如施工建筑下料问题中节约了材料，尽量减少残料的发生，合理下料，投资广告问题中获得预期的广告效果，集合料问题中如何取料运输费用最少，线性规划在诸如这些生活中的具体应用还有很多很多。