基于平板教学系统下的课前“精准预习”案例探究

沈旭东

中图分类号：G633.7文献标识码：A文章编号：1992-7711（2019）20-069-2

传统课前预习，教师对学生预习结果了解慢、收集难，并不能有效了解学生预习中暴露的薄弱点，预习只流于形式。幸而学校近年引进了平板教学系统，为笔者实施课前“精准预习”提供了硬件支持。在“精准预习”下，学生主体作用被进一步发挥出来，教师可以很快速地掌握学生预习过程中遇到的问题，在课前修改已经制定的学习目标，并针对性地制定教学内容。这对在课堂中实施精准教学，培养学生的核心素养提供了强有力的保障。本文以高考常见题型“动能定理与平抛、圆周运动相结合”的习题课为例，进行探究。

一、背景分析

从2018年6月开始，浙江省学业考试与高考重新分开命题。从已经开考的两次学考来看，“动能定理与圆周运动相结合”依旧是最后一题压轴题。而新政策下的高考卷虽未落地，但笔者可以猜测，“动能定理与平抛、圆周运动相结合”这类综合性很强的问题，极大概率是会被囊括在内的。该类问题很容易将物理概念、物理规律等与日常生活中的真实问题有机融合，以考查学生对物理概念、规律等的理解与应用。另外这类问题能检测出学生是否具有解决问题所需的各种科学思维方法和能力，符合课程标准中对学生核心素养的培养要求。

二、初步制定学习目标

学生已经在高一单独学习圆周运动和动能定理，也在高一初步接触过“动能定理与圆周运动相结合”的问题。基于该学情，在对学生发布预习作业之前，根据自身教学经验，初步制定对本节课的学习目标如下：

1.通过预习回顾，知道圆周运动的三种基本模型

2.通过例题，知道动能定理解题的规范化步骤

3.通过练习，理解解决动能定理与圆周运动相结合这类问题的解法

三、精准推送预习题目

基于已经初步制定的教学目标，挑选适量的习题作为预习作业（一般在15分钟左右），在前一天放学之前通过平板“作业平台”向学生推送（推送界面如图1），并在平台设定预习作业提交时间不得晚于当晚8点整。

本次预习作业如下：

如图甲所示的陀螺可在圆轨道外侧旋转而不脱落，好像轨道对它施加了魔法一样，被称为“魔力陀螺”。它可等效为图乙所示模型：竖直固定的磁性圆轨道半径为R，质量为m的指点沿轨道外侧做完整的圆周运动，A、B两点分别为轨道的最高点与最低点。质点受轨道的磁性引力始终指向圆心O且大小恒为F，不计摩擦和空气阻力，重力加速度为g。

（1）判断质点运动过程中机械能是否守恒，并说明理由;

（2）若质点在A点的速度为gR，求质点在该点对轨道的弹力;

（3）若磁性引力大小F可变，质点仍做完整圆周运动，求Fmg的最小值;

该题以竖直平面内的动能定理与圆周运动相结合为核心，结合生活中的玩具加以包装，是一道情景化运用的经典题型。题中质点是在轨道外侧运动，轨道对质点的弹力只能背离圆心向外，初看有点类似“拱桥模型”。但是由于磁性引力的存在，轨道对质点还存在一个指向圆心的吸引力，所以实际上该题的圆周运动是一个“杆模型”。可见该题虽计算量不大，但对思维要求较强，需要对题中描述的圆周运动模型进行辨别，生搬硬套就可能出错。通过对该题的求解，可复习回顾机械能守恒的条件、动能定理的规范化列式、圆周运动“绳模型”、“杆模型”、“拱桥模型”及其过最高点的条件等知识点。

四、及时汇总预习结果

以前传统预习作业，学生提交上来已经是第二天，教师在对学生反馈的问题处理上往往做不到非常全面。另外，传统预习作业需要手动统计学生上交情况，且很难对每个学生的长期的预习情况做出全面的评价，但通过平台提交形成大数据，我们可以一目了然地看到哪些学生按时提交，哪些学生迟交，哪些学生没交。并根据大数据中学生的每次预习的得分情况，清晰地掌握班级学生的学习情况，帮助学生清楚地知道自己的薄弱点。如图2，通过平台大数据得到的近三个月的作业数据，我们可以很清楚地知道学生提交作业情况，并针对性地对这些学生进行辅导。

五、快速评改预习作业

针对当晚上交的预习结果，利用平台进行批改，并将有错误的作业返回学生处进行订正。下面是针对本次预习作业的批改结果。

1.研究對象不明确，忽视牛顿第三定律的重要性

在解题过程中若涉及到受力对象的转换，必须用到牛顿第三定律。然而相比于牛顿第二定律，牛顿第三定律很少涉及计算，常常容易被学生忽视。该题解答时应选取质点（陀螺）作为研究对象，题目要求质点对轨道的压力，涉及到受力对象的转换。

如图3，该学生没有用牛顿第三定律把轨道对质点的弹力FN转化为题目要求的质点对轨道的弹力FN'。

2.最高点及最低点受力分析错误

不管是“绳模型”、“杆模型”、“拱桥模型”，需先进行受力分析，理清“什么力提供向心力”，再列出力学方程求解。

如图4该学生方框中的式子，受力分析时出现错误，导致力学方程错误。

3.建模错误，与“绳模型”混淆

仔细分析题目中的圆周运动，发现该模型为“杆模型”，该质点过最高点时的运动学条件为v=0。

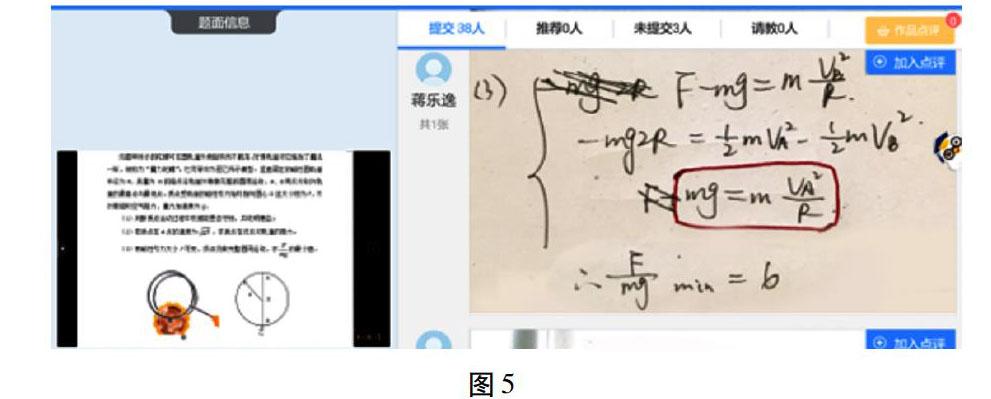
如图5所示，方框中的式子是“绳模型”中质点恰好过最高点的力学方程mg=mv2R，该学生模型混淆。

4.对圆周运动的临界条件理解模糊

在分析得到该题是一道“杆模型”的情况下，还需进一步分析解决第三问的临界问题。在考虑“杆”的强度的情况下，“杆模型”的临界条件可认为有两个（1）当“杆模型”恰好过最高点时有：力学条件mg=FN=0，运动学条件v=0。（2）满足“杆模型”恰好过最高点的条件下，要使质点过最低点时不脱离轨道，需满足FB-FN≥5mg。

如图6所示，该学生只考虑了最高点速度为零，却未考虑过最低点的临界条件。

六、基于学生反馈的学习目标调整

通过对预习作业的批改，发现学生的问题主要体现在以下几个方面：

1.牛顿第三定律未提起重视

2.对圆周运动的三种基本模型的基本特征了解不清晰

3.受力分析还需加强，最高点最低点的临界条件掌握不牢固

4.动能定理的书写不够规范

5.数学计算能力需要强化

基于以上的预习反馈，对已经制定的学习目标进行修正：

1.通过预习回顾，知道圆周运动的三种基本模型

2.通过习题，复习圆周运动过最高点最低点时的临界条件

3.通过例题，强化动能定理解题的规范化步骤

4.通过练习，理解解决动能定理与圆周运动相结合这类问题的解法

七、反思与总结

互联网+大数据+物理学科教学，使精准预习、精准教学得以有效实施。精准的、个性化的物理教学，大大丰富了课程资源，开拓了学生的视野，激发了学生的学习兴趣，提高个性化学习质量和学习效率。通过对数据的判断及分析，诊断并改进学生的学习问题，增强学生的学科优势，切实提高学生的学科素养。

（作者单位：浙江省吴兴高级中学，浙江 吴兴313000）