架空地线与预绞丝端口接触压力的仿真分析

吴勋, 尹创荣, 陈冠豪, 刘贯科, 杨睿, 郑文成, 郭德明

(广东电网有限责任公司东莞供电局，广东 东莞 523000)

架空地线一旦发生断线事故将会影响电力系统可靠运行，严重时将危及人们生命安全[1-4]。在实际当中，位于悬垂线夹处的地线表面通常缠绕上预绞丝以起防磨损和减振作用[5]，而预绞丝与地线之间接触良好与否关系到地线整体的力学性能。当线路发生故障时，工频短路电流将流经预绞丝与地线之间的接触部位[6-7]。由于接触电阻的存在以及电流相对集中，接触部位将产生大量的热能，使得地线抗拉性能因高温而下降，甚至直接熔断[8-10]。接触压力是衡量接触状况的一个重要因素，因此对预绞丝与地线之间的接触压力进行探究是十分有必要的。

国内外对绞制类导线力学性能的研究方法主要分为以下3类：①从导线几何结构层面入手，建立方程进行理论分析；②通过实验对导线的应力应变进行研究；③采用有限元仿真建立导线模型，研究导线相关力学性能[11-19]。赵新泽[11]等人通过有限元分析法建立绞制线邻层线股间微动接触模型，根据线股受力特点分析接触压力等微动参数对接触区应力分布的影响，并对仿真结果进行实验验证。LI Xiaoyong[12]等人基于Boussinesq势函数和弹性半空间模型，研究了椭圆赫兹接触面积和表面压力，利用表面接触量扩展了与椭圆接触有关的应力计算。MENG Fanming[13]等人采用一种新的半解析方法研究了钢丝间接触对钢丝绳绞线力学性能的影响，建立了钢丝绳在轴向拉伸和扭转载荷作用下的数学模型，将泊松比和线间接触的变形参数纳入模型。张秋桦[14]构建了股线受力平衡方程，对导线应力分布进行理论计算，利用导线的螺旋对称特点建立导线单股线模型进行仿真分析，设计安装导线拉伸试验测量装置。但目前对预绞丝与地线之间接触压力的研究较少，尚未对影响二者间接触压力的影响因素进行深入探究。

本文利用COMSOL软件建立预绞丝与地线接触端口模型，将预绞丝径向形变转化为等效轴向拉力，对仿真模型的边界条件进行加载设置，利用单一变量法分别研究预绞丝材料和预绞丝节距大小对二者之间接触压力大小的影响，并对仿真结果加以理论分析。

1 预绞丝端口稳态结构场有限元仿真模型的建立

1.1 架空地线悬垂串结构

悬垂线夹主要用于悬挂和紧握架空地线，而在实际线路安装布置中，通过在地线表面缠绕一层由若干根单股螺旋形金属丝绞合而成的预绞丝，以防止地线与悬垂线夹船体间发生磨损，增强线夹悬垂地线段的刚度[20]。除此之外，预绞丝还能够减小由于风力等外界因素造成的动弯应力，起到防震的效果[7]。图1为架空地线悬垂串结构。

由于预绞丝螺旋状的结构特征以及地线与预绞丝的力学特性，二者将在接触位置处相互挤压。位于图1左上方的局部放大图展示了地线与预绞丝径向接触状况。各接触横截面存在6个接触部位，在各个接触部位上，预绞丝将受到地线径向向外的接触压力F，而地线将受到预绞丝径向向内的接触压力。接触压力是衡量接触情况的一种重要因素，接触压力越大，二者之间的接触状况就越好。

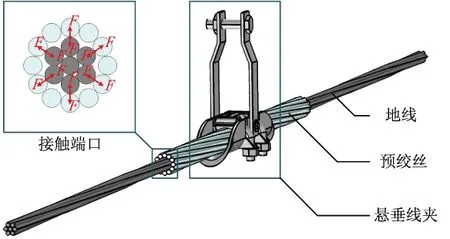
图1 架空地线悬垂串结构Fig.1 Structure of overhead ground wire suspension series

工频短路电流流经地线时，由于集肤效应，电流将通过预绞丝与地线之间的接触点从地线表面扩散至预绞丝表面。此时，预绞丝与地线的接触状况将与端口发热程度息息相关。在预绞丝与地线接触不良的情况下，二者间的接触电阻较大，预绞丝端口将会发热严重，从而造成地线强度下降，甚至有可能发生断股或断线的现象[21];因此，对预绞丝与地线之间的接触压力进行计算分析具有十分重要的意义。

1.2 预绞丝端口稳态结构场数学模型

结构分析常用于确定结构的位移、变形、应力和应变。本文通过结构场有限元仿真对预绞丝与地线进行结构分析，从而获得二者之间的接触压力大小。

在结构场有限元仿真中，由经典理论力学可知，物体的动力学方程为

Mx″+Cx′+Kx=F.

(1)

式中：M是质量矩阵；C是阻尼矩阵；K是刚度矩阵；x″是加速度矢量；x′是速度矢量；x是位移矢量；F是力矢量。

由于本文对预绞丝端口采用稳态结构场分析，故式(1)中与时间相关的量可被忽略，经化简可得下式：

Kx=F.

(2)

此外，为了避免仿真计算时接触点出现穿透现象，使得求解的结果更加精确，需要将存在接触的预绞丝和地线的表面设置为接触对，接触界面选用增广拉格朗日方法确定约束条件。

1.3 激励和边界条件的加载

预绞丝被缠绕上地线后将会发生径向形变，通过挤压地线形成接触压力。在实际工程应用中，二者之间的接触压力大小难以直接通过实验获取。为解决这一难点，本文通过对预绞丝加载一个等效轴向拉力以获得与实际相同的径向形变，从而间接模拟出预绞丝与地线之间实际的接触压力。

预绞丝在弹性形变范围内，其所承受的等效轴向拉力与轴向形变量满足下列关系

Fa=kε1.

(3)

式中：Fa为等效轴向拉力；k为预绞丝刚度；ε1为轴向形变量。

设预绞丝缠绕地线前(未发生形变)径向尺寸为c，预绞丝缠绕地线后(发生形变)的径向尺寸为c′，则

(4)

式中：Δc为预绞丝的径向形变量；μ为预绞丝的泊松比。

而预绞丝刚度

(5)

式中：G为预绞丝在常温下的切变模量；d为单根预绞丝的线径；Dm为整体预绞丝的中径；Nc为预绞丝的有效圈数。

整体预绞丝的中径和预绞丝的有效圈数分别为：

Dm=D0-d，

(6)

(7)

式中：D0为整体预绞丝的外径；l为预绞丝长度；y为预绞丝节距。

联立式(3)—(7)，即可得到等效轴向拉力Fa与预绞丝径向形变量Δc间的关系，即

(8)

通过实验可以得到预绞丝在缠绕地线前后的径向形变量Δc=4.25 mm，据此便可求出该径向形变量所对应的等效轴向拉力，并以此作为预绞丝模型边界条件加载的依据。

为减少有限元仿真计算的工作量，在建立模型时缩短预绞丝及地线模型的轴向长度。其中，预绞丝建模长度为9 mm，地线建模长度为15 mm。图2为预绞丝-地线模型示意图。

预绞丝端口边界条件在模型中的加载方式如图3所示。其中，A为固定约束面，对预绞丝下端面的若干根线股的横截面进行固定约束；B为等效拉力加载面，对预绞丝上端面若干根线股的横截面加载等效轴向拉力。

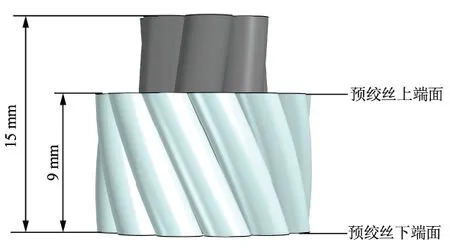
图2 预绞丝-地线模型示意图Fig.2 Schematic diagram of preformed armor rod and ground wire model

图3 预绞丝端口边界条件加载示意图Fig.3 Schematic diagram of boundary condition loading for preformed armor rod end

2 仿真结果与分析

2.1 不同预绞丝材料的接触力分析

本文通过建立3种不同材料且节距相同的预绞丝端口稳态结构场模型来分析不同预绞丝材料对二者接触点间的接触压力。其中，预绞丝分别采用镀锌钢绞线、铝包钢绞线、铝合金绞线，而地线的材料均为镀锌钢。表1所示为3种预绞丝材料的结构场物理参数。

表1 3种预绞丝材料的物理参数Tab.1 Physical parameters of three preformed armor rod materials

在模型几何参数设置中，预绞丝的节距取80 mm，预绞丝的线径取3 mm，地线的节距取130 mm，地线的线径取3 mm。根据铝包钢绞线的国家标准，预绞丝铝层的厚度范围为0.1～0.6 mm，本文仿真模型中取铝层厚度为0.3 mm。在实际工程应用中，镀锌钢绞线的镀锌层仅是为了防止外界环境对钢芯造成腐蚀，而对预绞丝的机械强度贡献不大;因此，本文在镀锌钢预绞丝端口模型的建立中，将锌层忽略不计，采用钢对钢的直接接触来模拟镀锌钢绞丝与地线的接触。

图4为铝合金预绞丝端口处接触压力的分布云图。

图4 铝合金预绞丝-地线接触点压力云图Fig.4 Pressure nephogram of contact point of aluminium alloy preformed armor rod and ground wire

由图4可知，当加载等效轴向拉力后，地线与预绞丝在线股间的切点发生接触，二者之间出现若干排接触点，每排接触点之间的距离为一固定值，且每个接触点的接触中心压力最大，并沿着接触边缘方向逐渐减小至零。对任意一根地线表面进行面积分，可以计算得到该表面单个接触点压力的大小。3种不同预绞丝材料镀锌钢、铝包钢、铝合金的单个接触点接触压力分别为101.86 N、84.49 N、44.25 N。切变模量是表征材料在受到外力作用下抵抗弹性形变能力的参数，在相同形变量的情况下，切变模量越大，材料抵抗弹性形变的反作用力就越大。这3种材料泊松比相近且径向形变量相同，镀锌钢的切变模量最大，故其接触压力也最大。

2.2 不同预绞丝节距的接触力分析

本文建立6种不同预绞丝节距且长度相等的预绞丝端口稳态结构场模型，分析不同预绞丝节距对二者接触点间的接触压力的大小的影响。以铝合金材料为例，预绞丝的节距分别取70 mm、80 mm、90 mm、100 mm、110 mm、120 mm。经仿真计算所得到不同节距下的单个接触点接触压力大小见表2。

表2 不同节距下单个接触点的接触压力值Tab.2 Contact pressure values of single contact point at different pitches

由表2可知，随着预绞丝节距的增加，单个接触点的接触压力逐步下降。图5为单根线股受力分析图。其中，Fl为股向力，F为接触压力，R为线股的曲率半径，α为线股所对应的夹角，圆点为线股中心位置。在数值上，F即为线股两端Fl在中心位置的合成力大小。

图5 单根线股受力图Fig.5 Force analysis chart of single strand

对于长度为一个节距的预绞丝而言，节距越大，展开平铺后所对应的线股长度L就越长。由于线股材质均匀且各向同性，线股各处的股向力大小相等。根据胡克定律[22]可知股向力满足

(9)

式中：E为铝股的弹性模量；A为线股横截面面积。故当预绞丝径向形变量相同时，预绞丝节距越小，其股向力就越大。对于等长的线股而言，由于节距越小其所对应的曲率半径越小，线股对应夹角小，经股向力合成后的接触压力较大。

3 结论

本文利用建立的预绞丝与地线接触端口的结构场仿真模型对预绞丝与地线之间的单个接触点的接触压力进行分析研究。同时，本文提出一种将预绞丝径向形变转化为等效轴向拉力的计算方法，用于获取建模仿真时所需的边界条件。基于预绞丝与地线接触端口仿真模型，利用单一变量法分别改变预绞丝材料与预绞丝节距来探究材料与节距对预绞丝与地线之间的单个接触点的接触压力大小的影响，并得到以下几点结论：

a)当预绞丝节距相同且线径尺寸相同时，预绞丝与地线接触点间接触压力的大小主要与材料的切变模量与泊松比有关。若材料泊松比相近，则随着切变模量的增加，二者间的接触压力也将逐步增加；若材料切变模量相近，则随着泊松比的增加，二者间的接触压力也将逐步增加。

b)当预绞丝材料相同且线径尺寸相同时，预绞丝与地线接触点间接触压力的大小主要与预绞丝的节距有关。随着预绞丝节距的减小，二者间的接触压力将随之增大。

c)根据上述仿真结果，电力工程中使用预绞丝接续或者修复导线、地线时，为保证有较好的接触导电特性，建议选择材料为镀锌钢的预绞丝，且其节距不宜过大。