Parameter Estimation for Complex Ornstein-Uhlenbeck Processes
PANYurong,SUNXichao
College of Science, Bengbu University, Bengbu 233000, China
Abstract: The drift parameter estimation problem of the complex Ornstein-Uhlenbeck process driven by a complex α-stable motion is considered. Based on discrete observations, an estimator of the unknown drift parameter is constructed by using the least squares method. Moreover, the strong consistency and the asymptotic distribution of the least squares estimator are derived under some assumptions.
Key words: α-stable motion; complex Ornstein-Uhlenbeck processes; the least squares estimation; consistency; asymptotic distribution
Introduction
dXt=-γXtdt+dζt,
(1)
Statistical inference for stochastic differential equations is an important research direction in probability theory and its applications, and there are many meaningful work and monographs for this direction[1-3]. When the driving processζis a standard Brownian motion in the SDE (1), the stochastic processXis an O-U process which was first considered and studied for its simple structure and good properties of the estimator (see Refs.[4-6]). Pan[7]studied the least squares estimation for O-U processes with periodic mean. The stochastic processXbecomes a fractional O-U process when the driving processζof the SDE (1) is a fractional Brownian motion. Some researchers have discussed the drift parameter estimation problem for fractional O-U process and generalized fractional O-U process[8-9]. Recently due to growing practical interest, the non-Gaussian α-stable motion caused some authors’ attention. The stochastic processXdefined by the SDE (1) is a non-Gaussian O-U process, which can be applied to model stochastic volatility in the non-Gaussian financial market[10]. Huetal.[11-14]have studied the parameter estimation problem for non-Gaussian O-U processes. In addition, parameter estimation problem of those O-U processes driven by other 1-dimensional motion also has been studied[15-18]. In all of the above-mentioned literatures, the driving processζis one dimensional process. However, the inference references related to stochastic equations driven by a complex process are very limited. We mention the works Arato and Sinai[19]and Chenetal.[20]for the drift parameter estimation of complex-valued O-U processes driven by a complex Gaussian process. It is natural to expect that complex O-U processes can be applied to model the stochastic volatility in the financial market or elsewhere in the future.
Recently, Vakeroudi[21]studied the windings of complex-valued O-U processes with a Brownian motion and an α-stable motion. Motivated by these results, the main focus of this paper is to construct the estimator ofγin (1) by using the least squares technique due to Chenetal.[20], and discuss the consistency and the asymptotic distributions of the estimator. For simplicity, we suppose thatω=0 andλ>0 in our discussion.
This paper is organized as follows. In section 1, we present some preliminaries about α-stable distribution and α-stable stochastic integrals. In section 2, we give some assumptions and main results of the present paper. In section 3, we prove the strong consistency of the least squares estimator. In section 4, we study the asymptotic distribution of the estimator. In section 5, we give some conclusions.
1 Preliminaries
In this section, we briefly recall some basic results of α-stable distribution and α-stable stochastic integrals. We can refer to the monograph of SAMORODNITSKYetal.[22]for more details about the related theory of α-stable process.
Definition1We say that a random variableηhas a stable distribution, denoted byη~Sα(σ,β,μ), provided the characteristic function ofηadmits the representation
whereα∈(0,2],σ∈(0,∞),β∈[-1,1] andμ∈(-∞,+∞).α,σ,βandμare called the stability index, the scale parameter, the skewness parameter and the location parameter, respectively. Whenμ=0, we callηis strictly α-stable, and moreover whenμ=0 andβ=0, the random variableηis called symmetric α-stable.
The next statements give some properties of α-stable stochastic variable which are given in Lemmas 1 and 2[22].
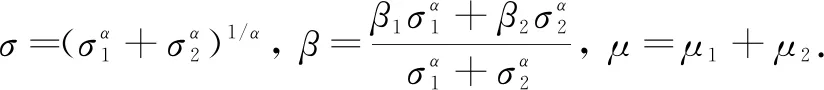
Lemma2Let a random variableξ~Sα(σ,β,μ) with 0<α<2, then we have
(Ⅰ)E|ξ|q<∞ for any 0 (Ⅱ)E|ξ|q=∞ for anyq≥α. In this paper, we are interested in the study of parameter estimation for the complex O-U process satisfying Eq. (1). To end this, we need some assumptions to obtain the results. Throughout this paper we assume thatCis a generic real-value constant possibly depending onαandγ, which may be different from line to line. Denote In addition, the selection ofhis related to stability indexαin this paper, we can see Remark 3.3 in Hu and Long[11]. Suppose that {Xt,0≤t≤T} can be observed at some discrete time instantstp=ph,p=1, 2, …,n. By the least squares method, we introduce the following contrast function of Eq.(1) (2) whereΔtp=tp-tp-1. We minimizeρn(γ). It is easy to see that the minimum ofρn(γ) is attained whenγis given by (3) On the other hand, Eq. (1) has the unique solution and its solution can be expressed as (4) Thus, Eq. (3) can be written as (5) In this paper, the main objects are to expound and prove the next theorems. Theorem2Under Condition (A1), we have In this section, we prove Theorem 1. Suppose that then we have (6) Notice that (7) We see that Eq. (5) can be represented as (8) So, it is easy to see that Λ1+Λ2, (9) (10) By Hölder’s inequality it follows that Combining this with Lemma 2, we find that (11) Clearly, we have (12) In order to prove Theorem 2, we need two lemmas which are given in [11]. Lemma4If Condition (A1) is satisfied, then we have whereU0,U1,U2,… are i.i.d with the same stable distributionSα(1,0,0),Y0~Sα/2(σ1,1,0). Lemma5Under Condition (A1), we have The paralysed girl sits in the warm sunshine and can see thewood and the lake; the world had become so large, so beautiful, andonly through a single word from the kind mistress of the mansion (13) Proposition1Under condition (A1), then asn→∞, Λn→0. ProofWe have (14) Next, we study the asymptotic behavior of Φ2(n). Proposition2Suppose that Condition (A1) is satisfied, then we have ProofByX0=1 and the Eq. (14), we get It follows that Φ21(n)+Φ22(n)+Φ23(n)+Φ24(n)+Φ25(n). which shows that Φ22(n)converges to 0 in probability, asnh→∞. On the other hand, by the Markov inequality, for anyε>0 we find that 2Cε-1n-2/αh1-2/αrh(1-e-γh)-2≤ which tends to zero under Condition (A1). As a direct consequence of Hu and Long[11], we see that Φ24(n) and Φ25(n)converge to zero in probability, asntends to infinity. Thus, we have introduced Proposition 2. (15) ProofNote that Φ11(n)+Φ12(n)+Φ13(n). (16) According to the Markov inequality, we find that D1(n)+D2(n). (17) By the Markov inequality, for anyε>0, we have that C(γε)-1(nhα-1logn)-1/α+Cγ-2ε-1(nh2α-1logn)-1/α, (18) Applying similar way to Φ13(n), we easily introduce (19) whereYandY′ are independent stable random variables with same distributionSα((αγ)-1/ασ2,0,0). Thus, Proposition 3 follows from Lemma 1. ProofCombining Proposition 1, Proposition 2, Proposition 3, (13) and (15), we introduce Theorem 2. This paper mainly deals with the parameter estimation problem for complex-valued O-U processes, extending the result of Hu and Long[11]to a special 2-dimensions. Assuming that the complex O-U process is observed at discrete time instantst=h,2h,…,nh. We obtain the least squares estimator of the unknown drift parameter. Through our research, we found that the least squares estimator is strongly consistent ash→0 andnh→∞ asn→∞, and give the rate of convergence of the least squares estimator under some assumptions.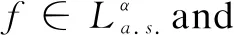
2 Assumptions and Main Results
2.1 Assumptions


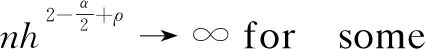
2.2 The least squares estimator and its properties

3 Proof of Theorem 1


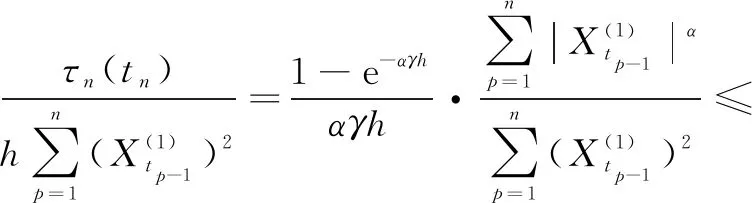
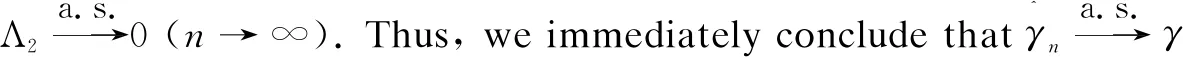
4 Proof of Theorem 2
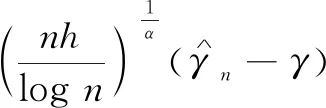

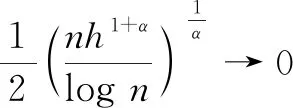
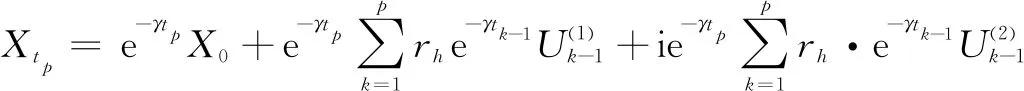
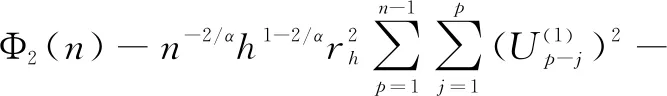


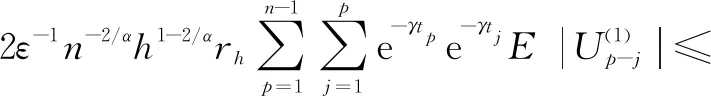

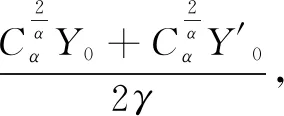


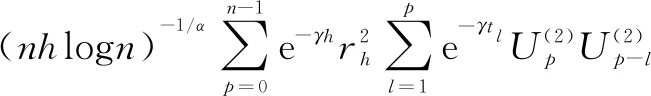
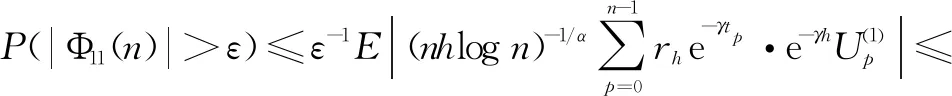
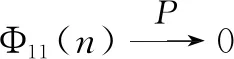
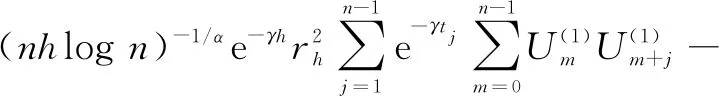


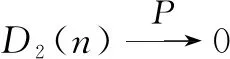
5 Conclusions
 Journal of Donghua University(English Edition)2019年4期
Journal of Donghua University(English Edition)2019年4期
- Journal of Donghua University(English Edition)的其它文章
- Elastic Predictions of 3D Orthogonal Woven Composites Using Micro/meso-scale Repeated Unit Cell Models
- Sound Character Calculation and Analysis of Sound Barrier Based on Acoustoelectric Analogy
- Tool Health Condition Recognition Method for High Speed Milling of Titanium Alloy Based on Principal Component Analysis (PCA) and Long Short Term Memory (LSTM)
- Upper Bound Solution of Soil Slope Stability under Coupling Effect of Rainfall and Earthquake
- Exploring the Performance of Magnetic Immobilized Lysozyme on Sludge Hydrolysis and Mechanism of Improving Dewaterability of Excess Sludge
- Mesoporous ZSM-5 Crystals Synthesized by a Novel Amphiphilic Organosilane Soft Template
