Upper Bound Solution of Soil Slope Stability under Coupling Effect of Rainfall and Earthquake

YINXiaojunWANGLanmin

1 Institute of Engineering Mechanics， China Earthquake Administration， Harbin 150080， China2 Key Laboratory of Earthquake Engineering and Engineering Vibration, China Earthquake Administration， Harbin 150080， China3 College of Mining Engineering， Heilongjiang University of Science and Technology， Harbin 150022， China4 Lanzhou Institute of Seismology， China Earthquake Administration， Lanzhou 730000， China

Abstract: Based on the limit analysis upper bound method， a new model of soil slope collapse has been proposed which consists of two rigid block zones and a plastic shear zone. Soil slope was induced failure by coupling effect of rainfall and earthquake， and these blocks were also incorporated horizontal earthquake force and vertical gravitate. The velocities and forces were analyzed in three blocks， and the expression of velocity discontinuities was obtained by the principle of incompressibility. The external force work for the blocks， the internal energy of the plastic shear zone and the velocity discontinuous were solved. The present stability ratios are compared to the prevenient research， which shows the superiority of the mechanism and rationality of the analysis. The critical height of the soil slope can provide theoretical basis for slope support and design.

Key words: soil slope； coupling effect； upper bound solution； stability ratio； earthquake； rainfall

Introduction

The landslides are one of the most serious disasters under earthquake. The most important objective of seismic stability analysis of soil slopes is the estimation of the seismic loads which will cause slippage of the soil mass of slope and the overall movements of the sliding soil mass of slope throughout an earthquake. Terzhaghi[1]simply based on adding an earthquake force to a static limit equilibrium analysis. Newmark[2]proposed a method for estimating the displacement of soil slopes during earthquake, and it addressed some of the crude assumptions of pseudo-static analysis.

Many studies have been performed to deal with the stability of soil slopes using the upper bound limit analysis over the past decades. Chenetal.[3-4]introduced a method to obtain the critical heights for homogeneous soil slopes by the upper bound method， and a rotational collapse mechanism bounded by an arc of the logarithmic spiral rupture surface was used in the analysis. Michalowski[5-8]also used the upper bound theorem of limit analysis in order to obtain the stability ratios for soil slopes in the presence of pore water pressure. Later， Michalowski again presented a direct approach which was based on a transitional collapse mechanism comprising of a number of vertical slices， and computed the stability ratios for homogeneous slopes in the presence of pore water pressures as well as pseudo-static horizontal earthquake body forces. Kumar[9-11]studied the stability ratios of soil slopes. Kumar and Samui[12]studied layered soil slopes using the upper bound limit analysis and got stability ratios under different conditions. The other researchers[13-16]also studied the stability of soil slopes by upper bound methods， and got corresponding stability ratios. Wangetal.[17-18]analyzed the stability of loss slope by shaking table tests under coupling effect of rainfall and earthquake.

However， the previous researches based upon the upper bound method have been reported only for simple shapes blocks including triangle or quadrilateral， and few focused on landslides owing to coupling effect of rainfall and earthquake. Two landslides (Yongguang village, Gansu province loess landslide, July 23, 2013; ABA State, Sichuan province, the new village of Fugui mountain burst high collapse, June 25, 2017) were the results of typical coupling effect of rainfall and earthquake. In this paper, by using the upper bound method of limit analysis， a new collapse mechanism has been proposed to determine the stability ratios of soil slopes under coupling effect of earthquake and rainfall， and the stability ratios can be subsequently used to analyze the given three kinds of soil slopes. The effect of the pore-water pressure and the pseudo-static horizontal earthquake body forces were also incorporated in the computations. The obtained values of the stability ratios of the model were compared with those reported in literatures.

1 Collapse Mechanism of the Problem

1.1 Definition of the problem

A two-dimensional soil slope with three sliding blocks is considered as shown in Fig. 1. The height of soil slope isHi(i=1, 2)； the total height of soil slope isH； the sloping surface is inclined at an angleαi(i=1, 2)； the width of soil slope base isβr0; the width of blockBCFbase isr0;βis a geometric parameter of the shearing zone； the collapse mechanism consists of three block regions， that is the shearing region for blockBNF， the rigid block regions forBCFandAMNB， and the stable region for blockNFP. Lines of blocks intersectionMN，BN，NF，BFandCFare lines of discontinuity (the blocks interface).

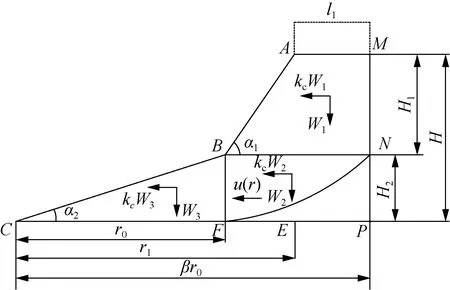
Fig. 1 Mechanism of soil slope collapse

1.2 Analysis of soil slope failure

1.2.1Forceoftheblocks

As shown in Fig.1， in the shearing zone，kcW2is a seismic force in the horizontal direction，kcis the critical acceleration factor，W2is the gravity force； in the rigid zone，kcW1andkcW3are the seismic forces in the horizontal direction，W1andW3are the gravity forces of the blocks， respectively.

1.2.2Velocityoftheblocks

In the shearing zone，u(r) is horizontal velocity andv0is vertical velocity； in the rigid block zone，u1(r) is horizontal velocity andv1(equaling to 0) is vertical velocity； in the stable zone， all velocities are zero. If the soil is assumed to rigid-perfectly plastic body， the velocity fields of the collapse mechanisms must satisfy the incompressibility condition:

whereuis horizontal velocity andvis vertical velocity.

The horizontal velocity at a horizontal distancermay be expressed as

(1)

2 Upper Bound Solution of Soil Slope Stability

The load[15]， determined by equating the external rate of work to the internal rate of dissipation in an assumed deformation mode(or velocity field)， satisfies velocity boundary conditions， strain rate and velocity compatibility conditions, and is not less than the actual collapse load. The load is the upper bound solution.

2.1 Work done of the external forces

The equations for each discontinuity may be obtained by satisfying continuity of velocity in the direction normal to the discontinuity line.

(2)

Work done of external forces in shearing zone and rigid zone is

dW=vvγdV+vhkcγdV,

(3)

wherevvandvhare the vertical velocity and horizontal velocity of shearing zone, andγis the bulk unit weight of soil.

The work done by gravity in regionAMNBis given by

(4)

whereφis the friction angle of soil.

The work done by seismic force in regionAMNBis given by

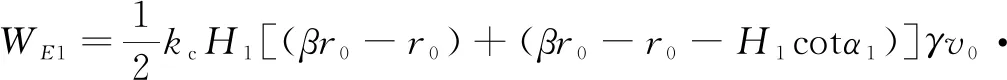
(5)

The work done by gravity in regionBFCis given by

W3=0.

(6)

The work done by seismic force in regionBFCis given by

(7)

The work done by gravity in regionBFCis given by

(8)

The work done by seismic force in regionBFCis given by

(9)

Therefore, the total work done is

WE=WG1+WE1+WG2+WE2+WE3，

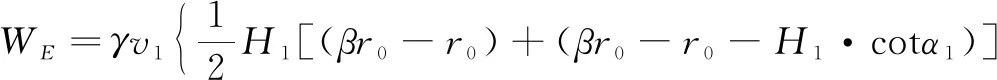
(10)

2.2 Energy dissipated along discontinuity

For a Tresca material， the energy dissipated along a discontinuity is[19]

(11)

where tanθ= dZMF/drandCuis undrained shear strength.

2.3 Energy dissipated with shearing zone

The Energy dissipated with shearing zone[20]is

(12)

whereεis the largest principal plastic strain rate， and

ε=du(r)/dr.

The total energy dissipated of the model is

ET=EMN+EBN+ENF+EBF+ECF+EBNF，

(13)

(14)

where，ruis the value of pore water coefficient， dlis the infinitestimal length of the element along the rupture surface， ΔWis the weights of the elements， anduwis magnitude of pore water pressure by the following expression.

2.4 Stability ratio of soil slope

The stability ratio[19-20]N=γH/Cuis obtained by equating the energy dissipated to the work done:

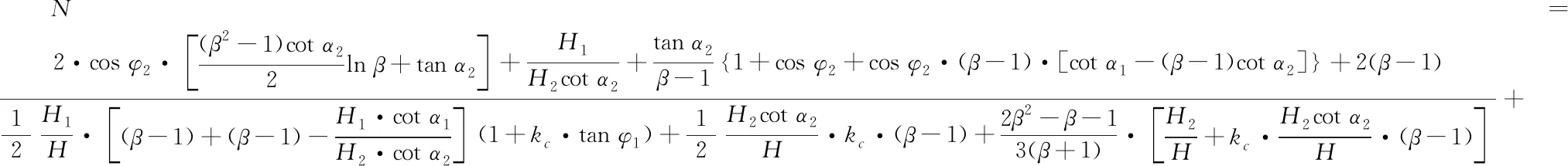
(15)

3 Computing of Stability Ratio

As a result， several variables relation in the expression (16):r0=H2cotα2，H1+H2=H，βr0-r0=H2(β-1)cotα2，r1=H1cotα1+H2cotα2， it should be noted that the value ofNwill become a function the following parameters:

(16)

For a given geometry of the soil slope， the functionFcan be minimized with respect to variables (H1/H，H2/H，α1，α2，β).Nmay be compute by the software of Matlab.

The critical heightHcof the soil slope can be got when theNminis given:

(17)

4 Analyses

By keeping the values ofH2/Hfrom 0.2 to 0.8，φ1=10°，φ2=20°；α2=25°，α1=30°-75°， the failure patterns were plotted for four different cases， namely: (I)kc=0，ru=0； (II)kc=0，ru=0.25； (III)kc=0.1，ru=0； (IV)kc=0.1，ru=0.25.

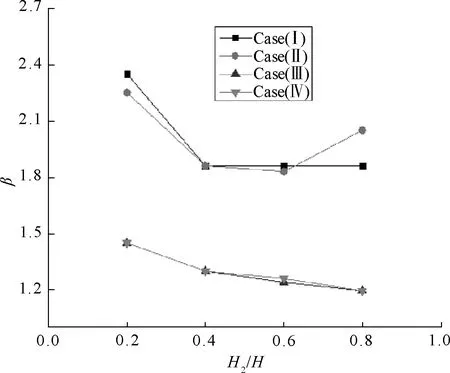
As shown in the mechanism(Fig.1)， the width of the plastic zone is (β-1)r0>0， which is related toH. According to variable ofr0/H，H1/H，H2/Hrelations， (β-1)H=m·H2is given， wheremis a coefficient related to cases (I)-(IV). The variation ofβwithH2/His given in Figs. 2(a)-(b).

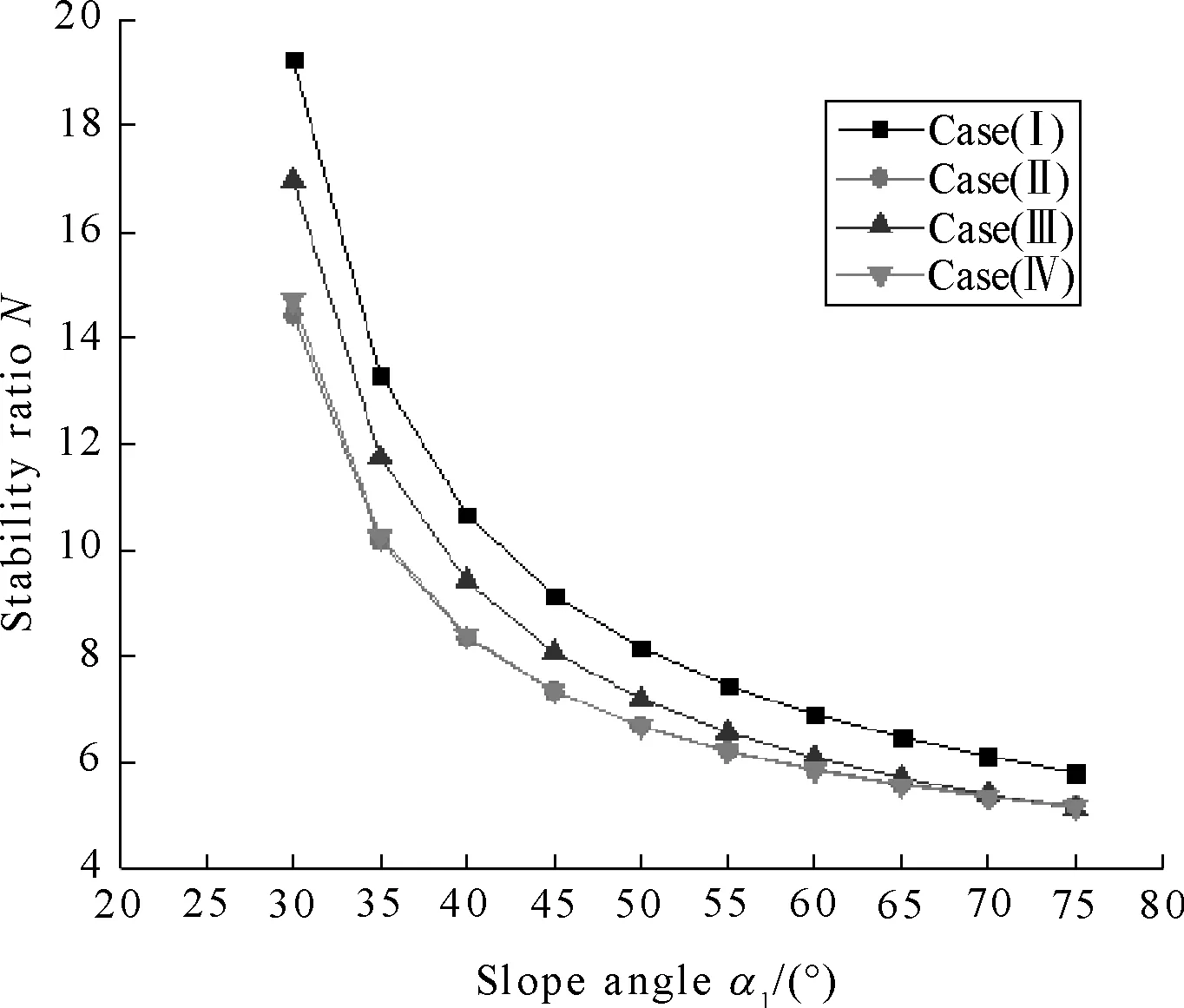
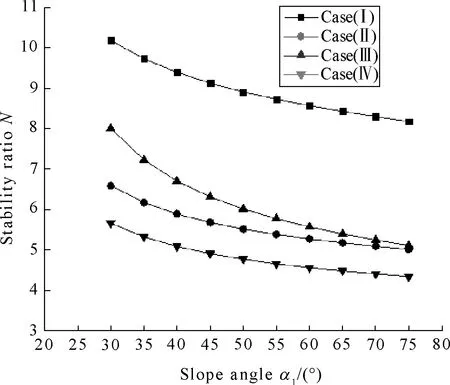
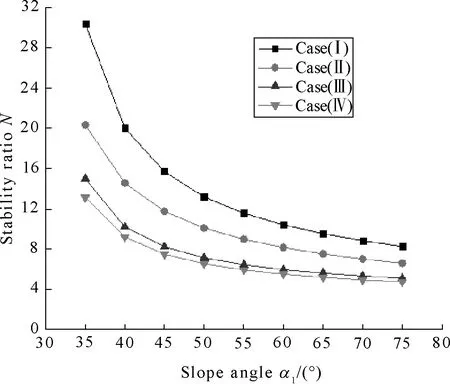
Stability ratios of soil slopes are noted byN1，N2，N3andN4respectively. These failure patterns are illustrated in Figs.3(a)-(d)， Figs.4(a)-(b)， Figs.5(a)-(d) and Figs. 6(a)-(d).

(a) φ1=10°

(b) φ2=20°

(a) H2/H=0.2

(b) H2/H=0.4

(c) H2/H=0.6

(d) H2/H=0.8

(a) H2/H=0.4

(b) H2/H=0.6

(a) kc=0， ru=0

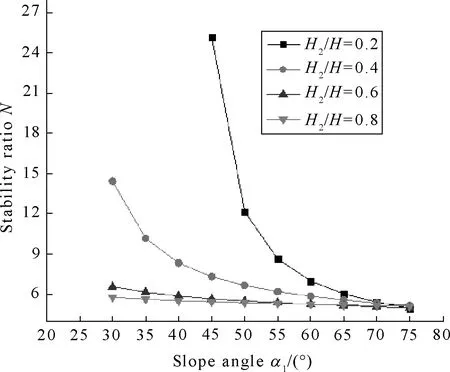
(b) kc=0， ru=0.25

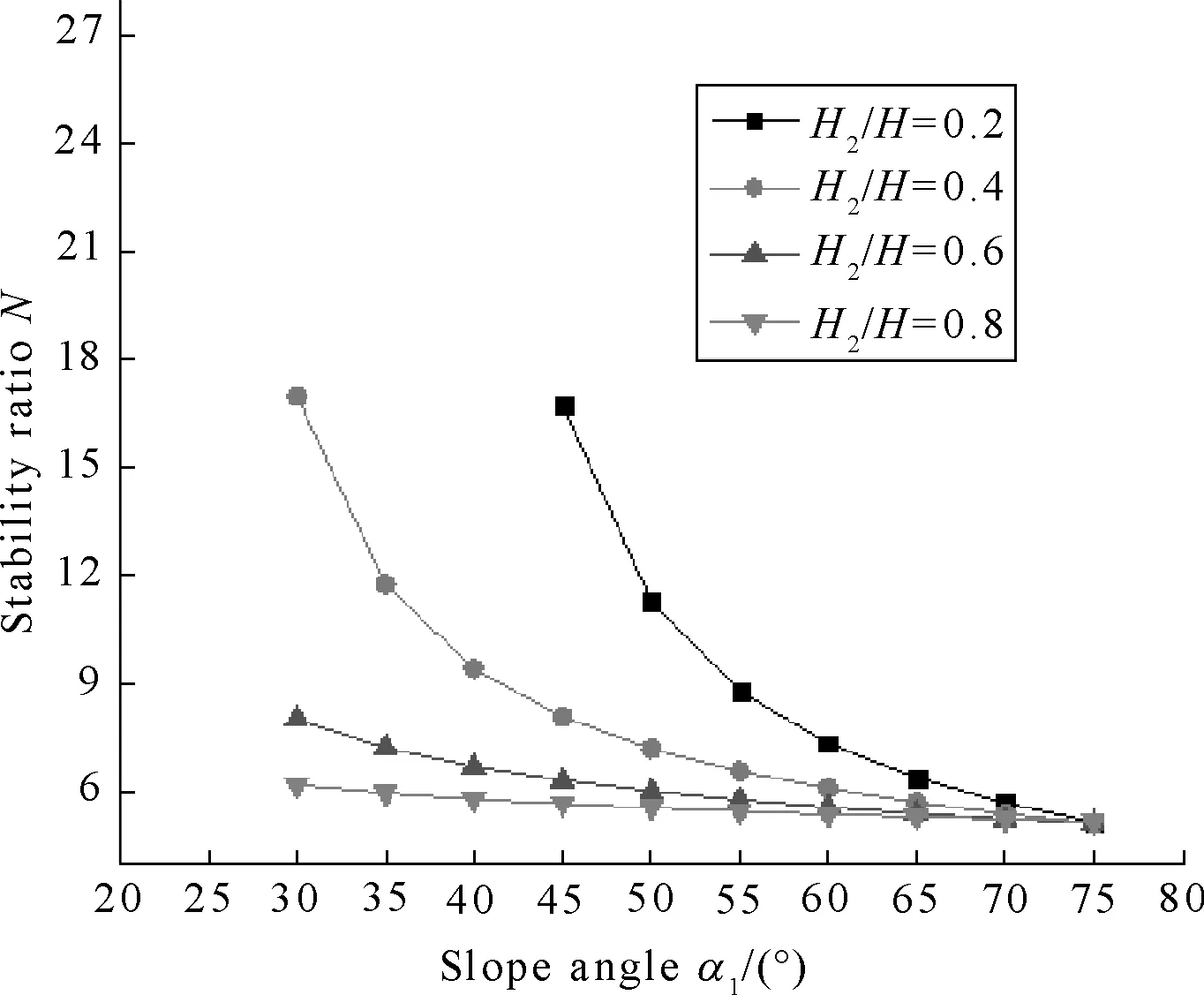
(c) kc=0.1， ru=0

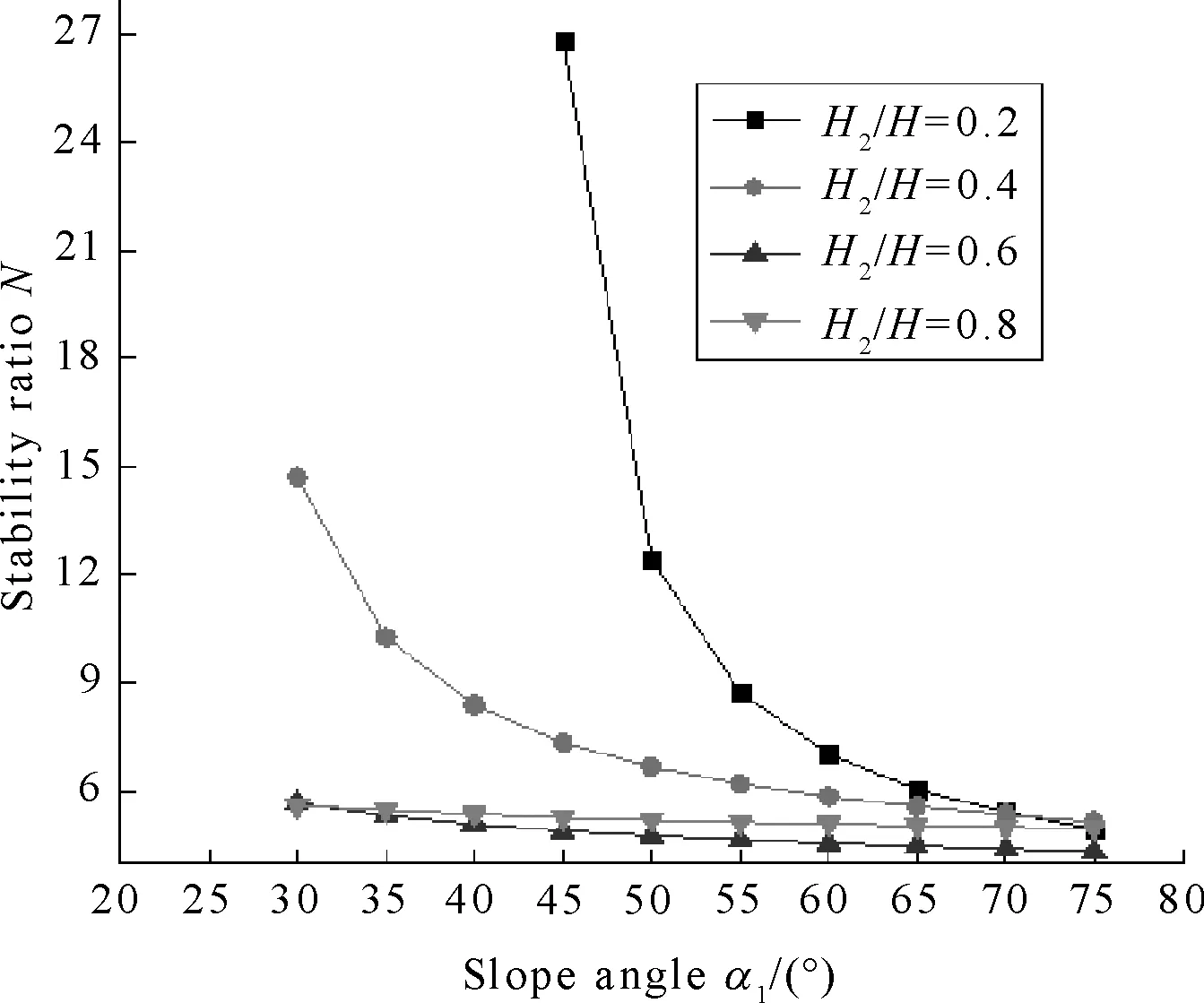
(d) kc=0.1， ru=0.25

(a) kc=0， ru=0

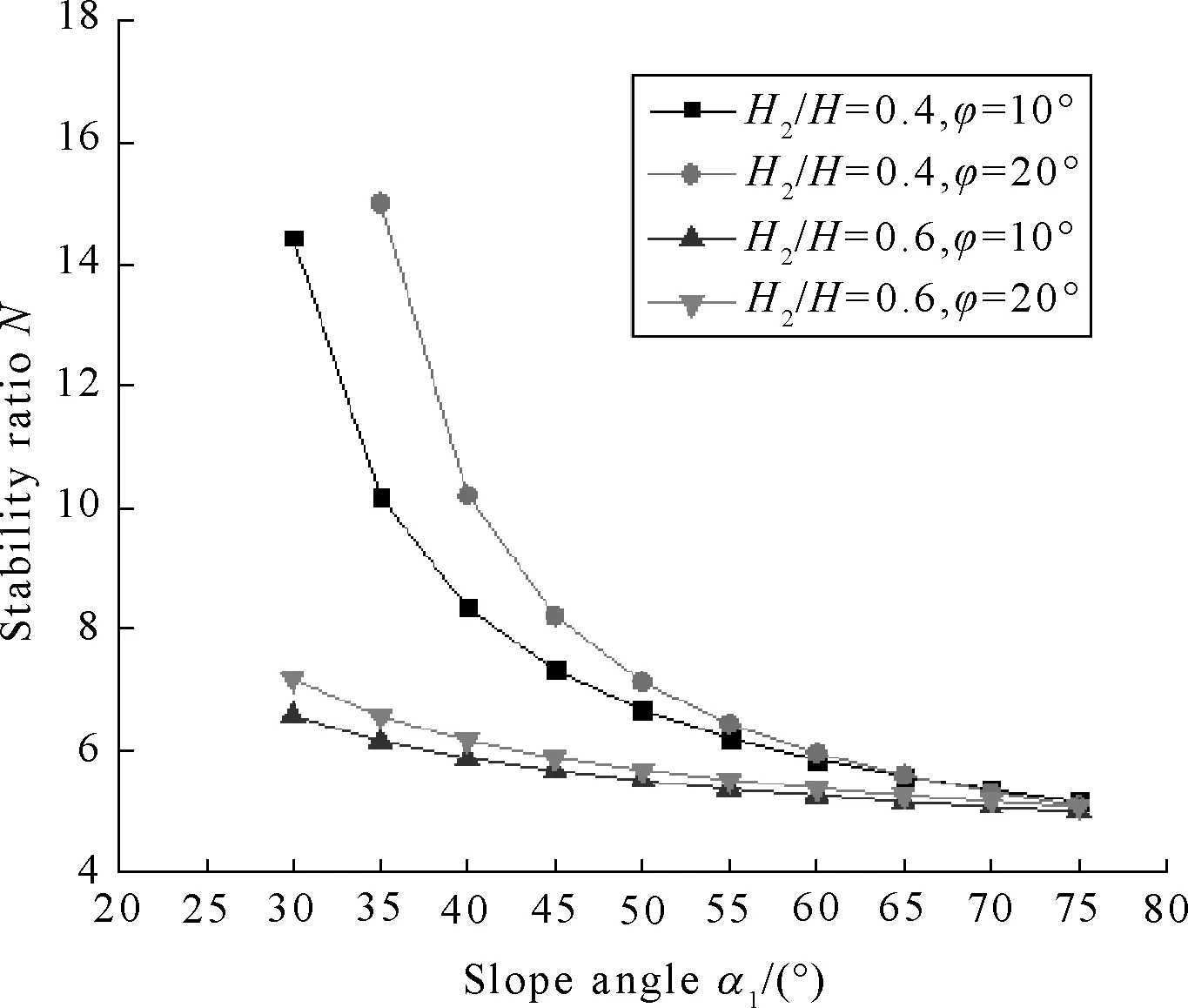
(b) kc=0，ru=0.25

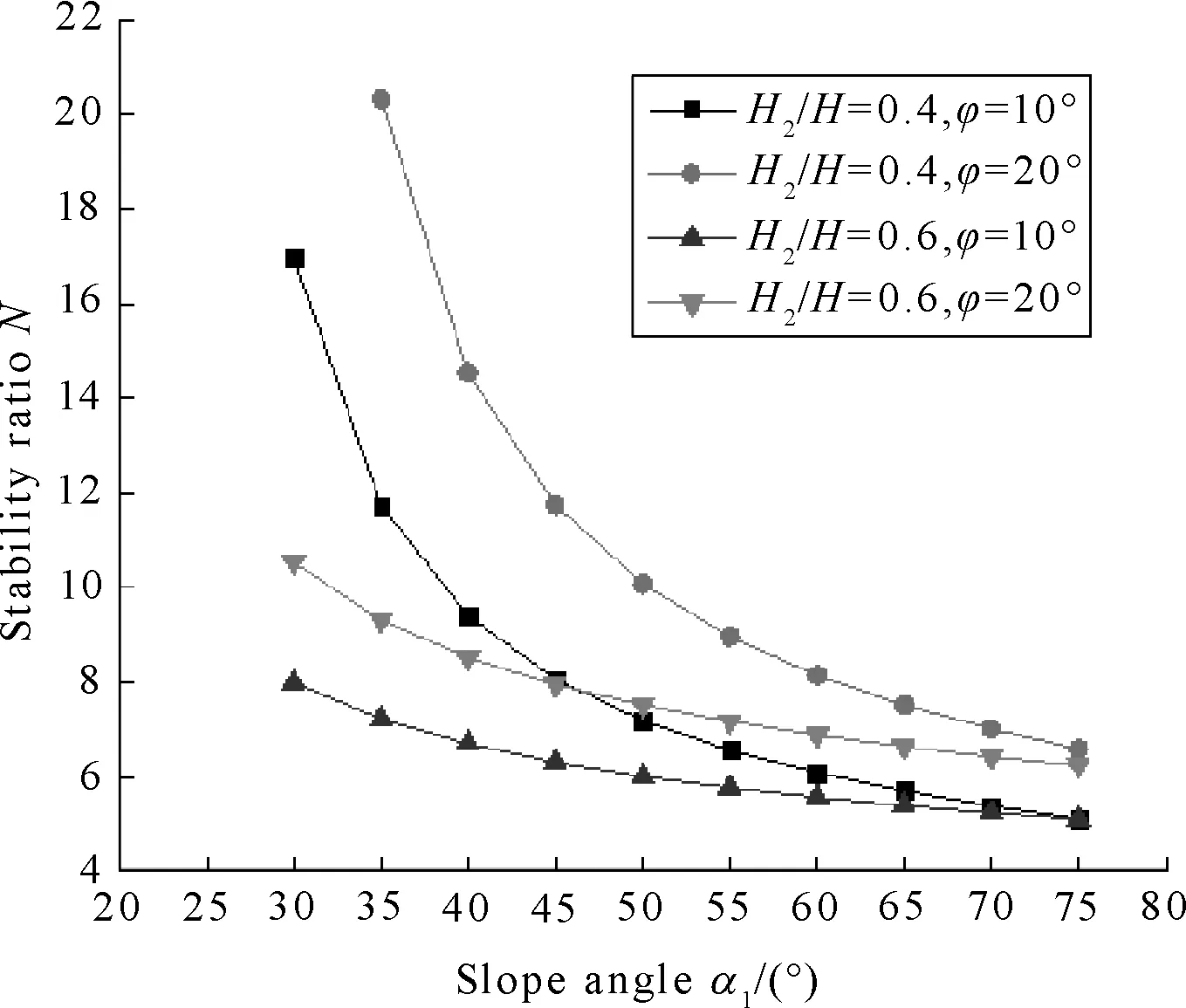
(c) kc=0.1， ru=0

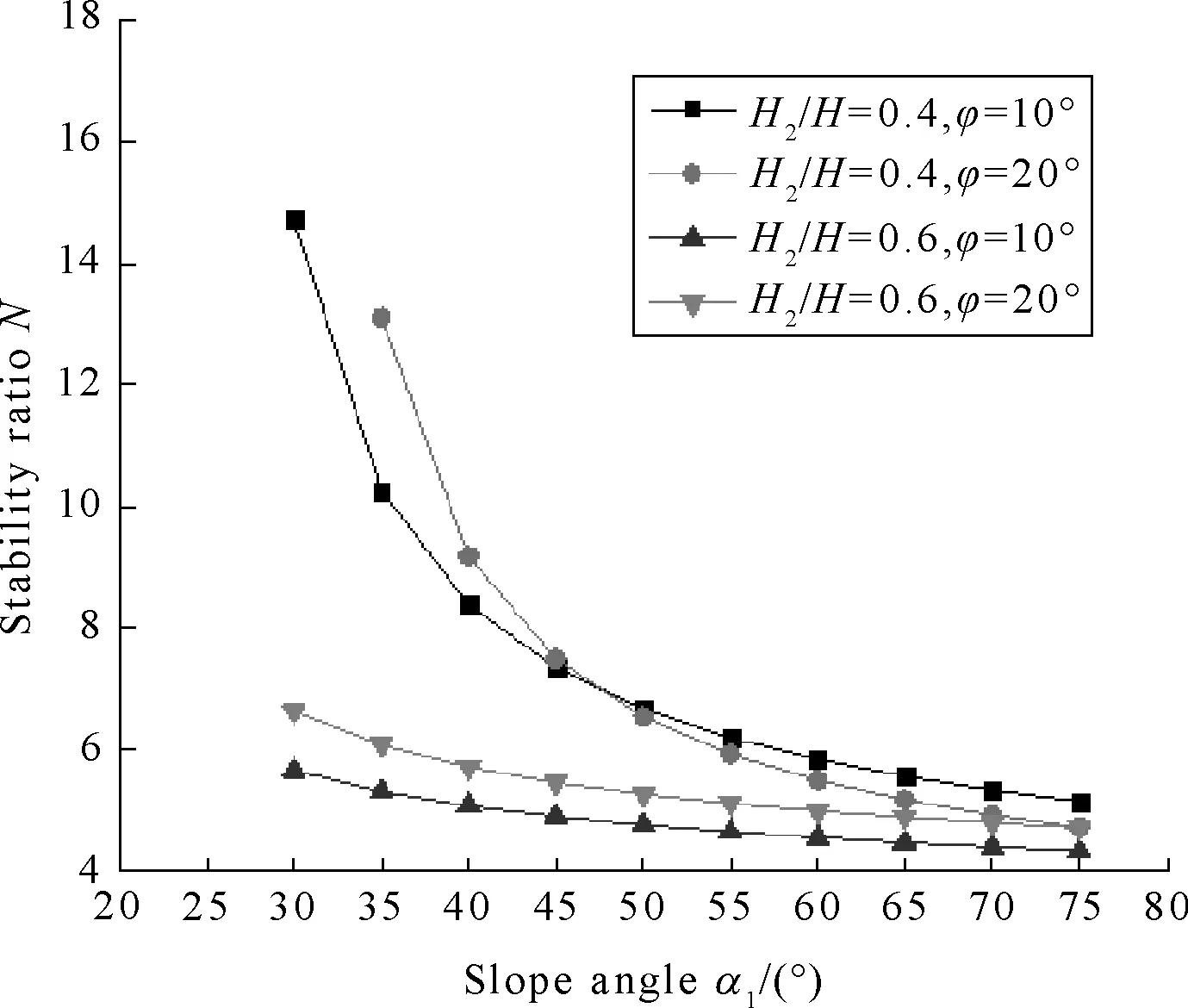
(d) kc=0.1， ru=0.25

φ/(°)α1 /(°)Present studyRef. [3] Ref. [11]10755.5025.805.801606.9057.267.259459.1259.329.31220758.1197.487.477609.0410.3910.3924515.6716.1816.181

Table 2Comparison of stability ratioNforkc=0.1 andru=0

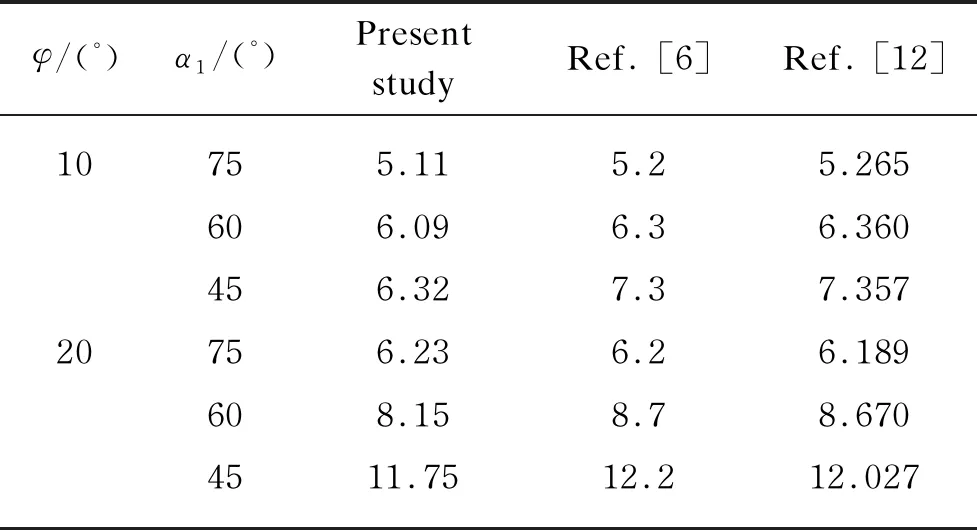
φ/(°)α1 /(°)Present studyRef. [6]Ref. [12]10755.115.25.265606.096.36.360456.327.37.35720756.236.26.189608.158.78.6704511.7512.212.027

Table 3Comparison of stability ratioNforkc=0 andru=0.25

φ/(°) α1 /(°)Present studyRef. [6]Ref. [12]10754.9885.25.186605.8696.36.389457.3377.77.95520755.0975.55.771605.9667.77.702458.22310.610.948

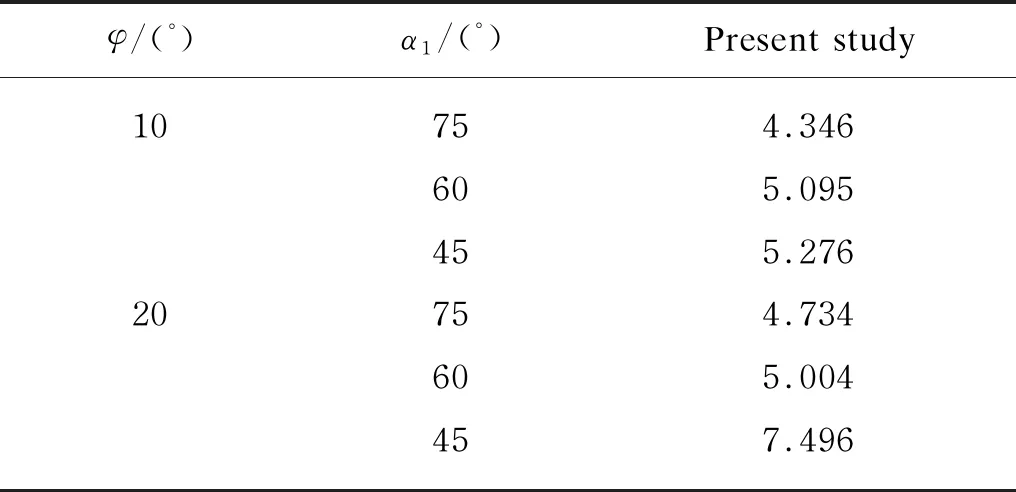
Table 4 Stability ratio N for kc=0.1 and ru=0.25

5 Discussion

Figures 3-6 indicate thatNdecreased whenα2=25°，φ1=10°，φ2=20°，α1from 30° to 75°，H2/Hfrom 0.2 to 0.8，Ngot the smallest value whenα1=75°. Stability ratios of soil slope have been found to decrease continuously with (i) increase inα1； (ii) increase inkcand (iii) increase inru.

Figure 3(a) shows thatN1>N2>N3>N4whenα1from 55° to 75°，N1is only slightly bigger than the other， butNis unreasonable whenα1from 45° to 55°， it may be parameters to optimize. Figure 3(b) shows thatN1>N2>N3>N4whenα1from 30° to 75°，N3is almost equal toN4，especiallyN2，N3andN4also almost same whenα1from 60° to 75°， it shows thatNlittle changed in the cases (II)-(IV) whenα1was more bigger. Figure 3(c) indicate thatN1>N2>N3>N4whenα1from 30° to 75°， andNis more obvious vary in the four cases. Figure 3(d) indicates thatN1>N2>N3>N4whenα1from 30° to 75°，N1fared more than the other，N2is almost equaled toN3whenα1from 60° to 75°.

Figures 4(a)-(b) indicate thatNvaried whenα1from 30° to 75° andφ2=20°， as it is expected，N1>N2>N3>N4，andN3was slightly biggerN4. Figures 5(a)-(d) show thatNvaried whenH2/Hrespectively equals to 0.2，0.4，0.6 and 0.8. Figures 6(a)-(d) indicate thatNvaried whenφ1=10° andφ2=20°，H2/H=0.4 andH2/H=0.6 in the fourth cases.Nis more bigger whenφ2=20° andH2/H=0.4.

Tables 1-3 show thatNmore smaller than previous results whenα1equals to 45°， 60° and 75° in the cases (I)-(III). Table 4 gives value ofNin the fourth case(kc=0.1，ru=0.25)， which isNminin the coupling effect of earthquake and rainfall.

According to limit analysis with associative flow rule， shape of slipped surface was mainly relevant to magnitude of friction angle. However， the slipped surface of collapse mechanism was not the best optimum. Therefore， it needs a more optimized slope model and parameters of soil.

6 Conclusions

Based upon the theory of limit analysis upper bound， the method of block limit analysis has been suggested to compute the stability ratios for soil slope during coupling effect of rainfall and earthquake.

The present results were more optimized than previous results in the certain range， and it showed that the optimization of collapse mechanism was correct and reasonable of the analysis.

The critical height of soil slopeHccan be gotten when the stability ratioNminobtains the minimum for given parameter values.

Block limit analysis method may be used to compute more complicated stability of soil slope subsequently.