Elastic Predictions of 3D Orthogonal Woven Composites Using Micro/meso-scale Repeated Unit Cell Models

JIAXiwen，GAOLimin(高丽敏)，ZHANGTian(张田)，ZHANGFa(张发)，WANGYan(王岩)

Department of Structural Integrity， Beijing Aeronautical Science & Technology Research Institute of COMAC， Beijing 102211， China

Abstract: This presentation predicts the elastic properties of three-dimensional (3D) orthogonal woven composite (3DOWC) by finite element analysis based on micro/meso repeated unit cell (RUC) models. First， the properties of fiber yarn are obtained by analysis on a micro-scale RUC model assuming fibers in a hexagonal distribution pattern in the polymer matrix. Then a full thickness meso-scale RUC model including weft yarns， warp yarns， Z-yarns and pure resin zones is established and full stiffness matrix of the 3DOWC including the in-plane and flexural constants are predicted. For thick 3DOWC with large number of weft， warp layers， an alternative analysis method is proposed in which an inner meso-RUC and a surface meso-RUC are established， respectively. Then the properties of 3DOWC are deduced based on laminate theory and properties of the inner and surface layers. The predicted results by the above two alternative methods are in good experimental agreement.

Key words: composite； multi-scale analysis； repeated unit cell model； finite element method

Introduction

Three-dimensional (3D) orthogonal woven composite (3DOWC) has three different types of fiber yarns， namely as weft yarns， warp yarns and Z-yarns. These three types of non-crimped yarns are placed in three mutually orthogonal directions[1]. Compared to conventional laminated composites and other types of textile composites， 3DOWC can have higher stiffness and strength along thickness directions. Currently， 3DOWC has been pursued in the aerospace industry primarily to improve the vulnerability of conventional laminates to de-lamination under impact and subsequent local buckling failure under in-plane compression[2]. Evidently， the understanding of the mechanical property of 3DOWC is required for practical applications.

The mechanical behaviors of 3DOWCs under quasi-static loadings have been investigated based on experiments and theoretical analyses. As to the experimental studies， attentions are focused on the tensile strength and failure mechanisms[3-11]， compressive characteristics[11-15]and shear responses[11， 16]. For the theoretical investigations， predictions of global properties of 3DOWCs are most commonly based on analyzing a representative volume element (RVE) or a repeated unit cell (RUC) model. Kimetal.[17-18]investigated the elastic properties of 3DOWCs based on direct numerical simulation (DNS) at RVE level. A unit structure including the stuffer yarns， filler yarns， weaver yarns， and the resin region was generated to numerically model the complex geometry of 3DOWCs. Based on the composition rule of fiber and matrix[19]， Kuo[20]estimated the engineering elastic constants of 3D orthogonal woven carbon-carbon composite based on a unit cell model and then applied them to study the behavior of a notched 3DOWC beam. Using the laminate block models and unit cell model， Tanetal.[21-24]analyzed the mechanical properties of 3DOWCs by analytical approach and finite element analysis (FEA) method at micro/macro-scale levels. Based on a 3D mosaic unit cell model， Bogdanovich[25-26]predicted the failure initiation and ultimate failure strains and loads， as well as characteristic features of progressive failure processes. Furthermore， the modeling strategies for other types of 3D woven composites can be referred to the review article[27-28]and many references therein.

The above-mentioned RVE models including DNS， laminate block and mosaic models have made different degrees of simplification on the complex fabric architecture in the 3DOWC and may not be able to provide accurate details of local stress distributions at fiber or fiber yarn scale levels. In addition， the “plane-remains-plane” boundary conditions were commonly applied either in the analytical or numerical analyses. In fact， the “plane-remains-plane” boundary conditions are over-constraint boundary conditions under shear loadings as indicated in Refs.[29-30]. Furthermore， two-step homogenization method was applied to predict the high-crimp woven composites[31].

A multi-scale analysis method based on analysis of repeated unit cell models (RUCs) at micro-scale RUC and meso-scale levels have been used to predict mechanical properties and damages for various laminated and textile composites. At micro-RUC level， the properties of fiber yarn are first obtained and then at the meso-scale RUC level， the global properties of the composites are predicted. The meso-RUC is constructed according to the actual fiber yarns architecture in the composite. Therefore， the accurate local stress distribution， which is essential to damage analysis， can be obtained.

As an extension of our previous researches[32-35]， the full elastic stiffness matrix of 3DOWC is predicted based on finite element analysis on the micro/meso RUC models. The predicted results by the above two alternative methods are in good experimental agreement， and the above-mentioned results are consisted with the effect of fiber architecture on tensile fracture of 3D woven textile composites[36]. 3D woven composites offer higher damage tolerance and resistance to delamination. The results show that there is an architecture dependent strain field and these localizations lead to the onset of failure in these materials.

1 Multi-scale RUC Models

1.1 Micro-RUC model for fiber bundle

Fiber bundles exist in a form of fibers with matrix in the 3DOWC. In the micro-RUC model， the yarns are usually considered as unidirectional fiber reinforced composite with periodic distribution of fibers in matrix. Based on the fiber packing patterns in matrix， a hexagonal model was widely applied for modeling transversely isotropic property of fiber bundles. In this analysis， based on the hexagonal fiber distribution， a rectangular micro-RUC model is selected as shown in Fig.1. The fiber volume fraction is taken to be 73.5% in the micro-RUC model.

(a) Fibers packing pattern

(b) Micro-RUC of fiber bundles to be meshed

1.2 Meso-RUC model for 3DOWC

In the current study， a 3DOWC of E-glass fiber with AROPOLTMINF80501unsaturated polymer matrix is analyzed. The composite was manufactured by the vacuum assisted resin infusion (VARI) molding technology and its specification is listed in Table 1.

Table 1 Specification of 3D orthogonal woven fabric

Through burning a cubic specimen in a griddle， nearly 64.1% weight of the specimen was reserved. The total fiber volume ratio of the 3DOWC is therefore obtained about 43.7% by the density of 2.55 g/cm3for the fiber and 1.22 g/cm3for the matrix. From the photographs of the 3DOWC as shown in Figs. 2 and 3， it can be seen that the weft yarns， warp yarns and Z-yarns are perpendicular to each other in straight lines and all the yarns have an approximate rectangular cross section.

Fig. 2 Photograph of 3D orthogonal woven fabric

(a) Surface

(b) Cross section along warp direction

Based on the linear density of fiber bundles with matrix in weft and warp yarns as provided in Table 1 and totally thickness of 9.64 mm with 33 layers of fiber bundles， the structural dimensions of the full thickness meso-RUC for 3DOWC are determined and it is shown in Fig. 4(a) and Tables 2-3. For clearance of the architecture of the meso-RUC， the architectures of the matrix， weft yarns， warp yarns and Z-yarns in the RUC are displayed separately in Figs. 4(b)-(e). The volume fraction of the fiber yarns in the meso-RUC model for 3DOWC is obtained about 59.5%. Correspondingly the fiber volume fraction in the micro-RUC is calculated as 73.5%. Note that a thin layer of the matrix with thickness of 0.1 mm is added at the top and bottom surfaces of the meso-RUC.

(a) Full (b) Matrix (c) Warp yarns (d) Weft yarns (e) Z-yarns

Table 2 Meso-structural parameters of 3DOWC

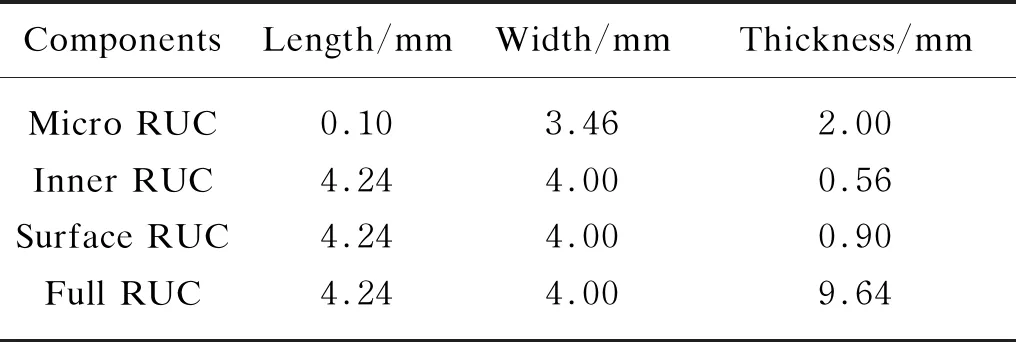
Table 3 Sizes of micro/meso-RUC and sub-RUCs

2 Alternative Method Based on Sub-RUC Models of 3DOWCS

The full thickness meso-RUC of 3DOWC shown in Fig. 4 is constructed by a number of repeated inner layers in the middle and two surface layers on the top and bottom. For clearance of the interior architecture of the sub-meso-RUC， the systems of yarns and matrix in the sub-meso-RUC are shown separately in Figs. 5-6.

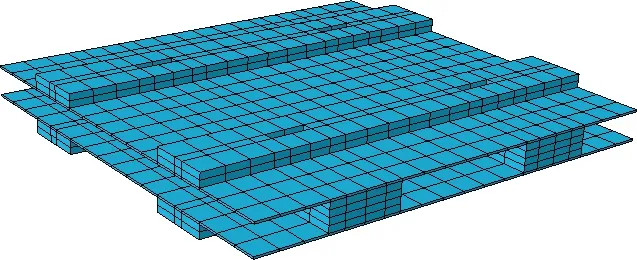
(a) Architecture of yarns system (b) Architecture of matrix

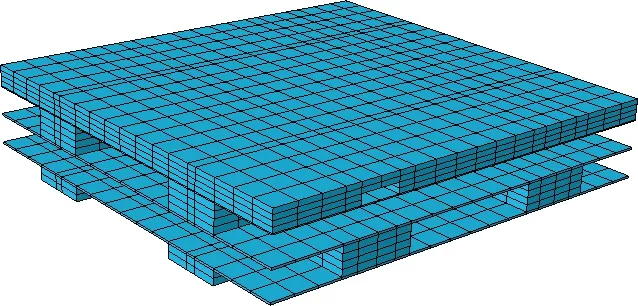
(a) Architecture of yarns system (b) Architecture of matrix

The essential differences in architecture of the surface and inner layers could result in quite different stress/strain distribution characteristics under the load. For 3DOWC with relatively large number of layers in thickness direction， to reduce the model size and CPU time， the following alternative modeling method is suggested. The periodic boundary conditions (PBCs) are applied by master and slave nodes technique for full meso-scale， inner meso-scale and surface meso-scale RUCs in detailed statement[32].

The analysis is carried out on the inner meso-RUC and the surface meso-RUC， separately. The full compliance matrix of the 3DOWC can be derived from the compliance matrices of the above two sub-meso RUCs based on the classical laminate theory.

3 Results and Discussion

3.1 Mechanical analysis for micro-RUC

Through the FEM analyses on the micro-RUC， Fig. 1(b) and its component (fiber/matrix) property ofE=72.5 GPa andν=0.22 for fiber andE=3.6 GPa andν=0.35 for AROPOLTMINF80501， by applying the six simple loading cases， respectively， the nine elastic constants of the fiber yarn are obtained and they are listed in Table 4. It can be seen that the highest modulus is in the fiber direction and the transversely isotropic properties of the fiber yarn have been well predicted. The results are consistent with previous research results based on the statistically equivalent fiber distribution[34]. In addition， the present method can also yield detailed stress distributions inter/intra-fibers in yarns.

Table 4 Elastic parameters being predicted for micro-RUC

Note： 1-fiber direction; 2，3-transversely cross-section directions.

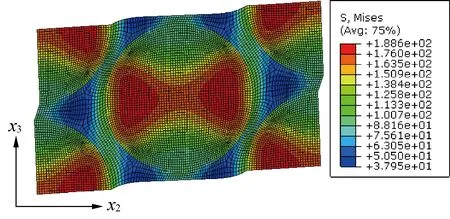
Fig. 7 Deformation and stress distribution of micro-RUC

3.2 Mechanical analyses for meso-RUCS

3.2.1Analysesforfullmeso-RUCS

For the full thickness meso-RUC of 3DOWC in Fig. 4(a). The nine elastic constants of the 3DOWC based on analysis to the full thickness meso-RUC are listed in Table 5. The tested elastic modulus ofE11=20.94 GPa[32-33]in warp direction are in good agreement to predicted results ofE11=22.31 GPa.

3.2.2Analysesforsub-meso-RUCS

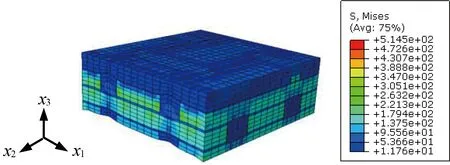
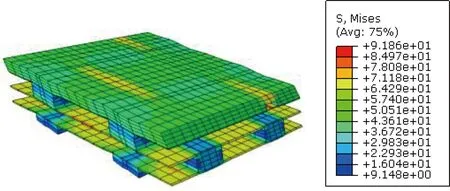
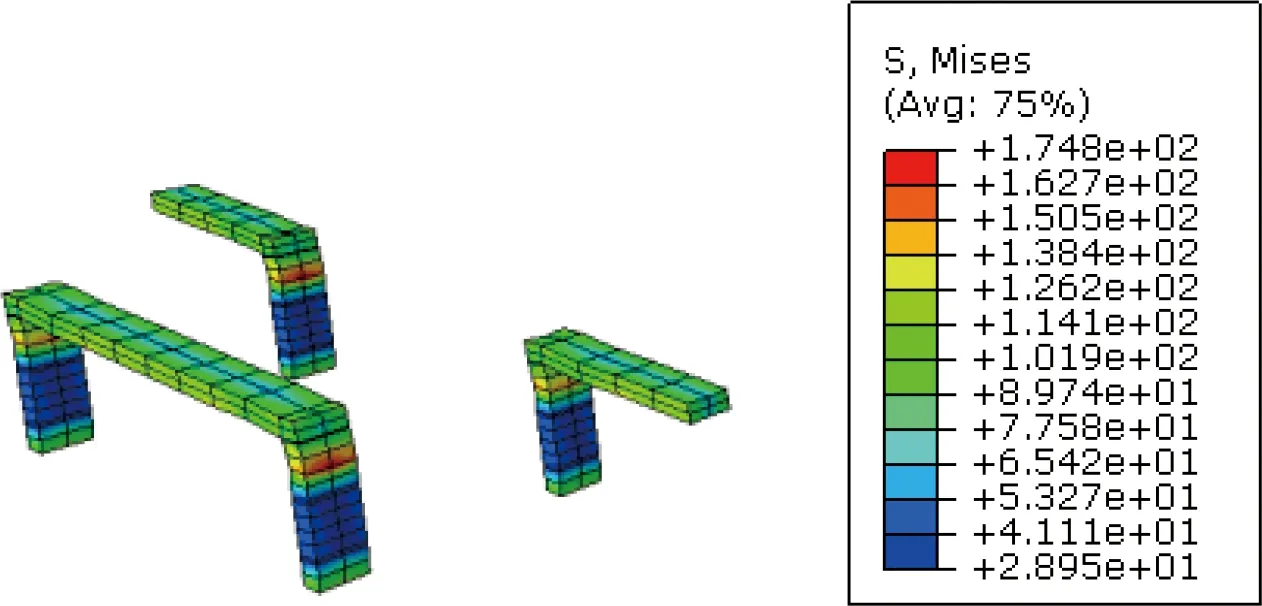
Based on analyses on the inner and surface meso-RUCs shown in Fig. 5， their elastic constants are also listed in Table 5. Obviously， the inner layer has higher tensile and shear modulus than that from the surface layer， which is consistent with denser array of fiber bundles in the inner part of the 3DOWC. Furthermore， the detailed von Mises stress distributions of the sub-RUCs under in-plane loadings are shown in Figs. 8-11， respectively.

Table 5 Elastic parameters being predicted based on RUC and sub-RUCs

Note： 1-warp yarn direction;2-weft yarn direction;3-Z-yarn direction.

(a) Inner RUC

(b) Matrix

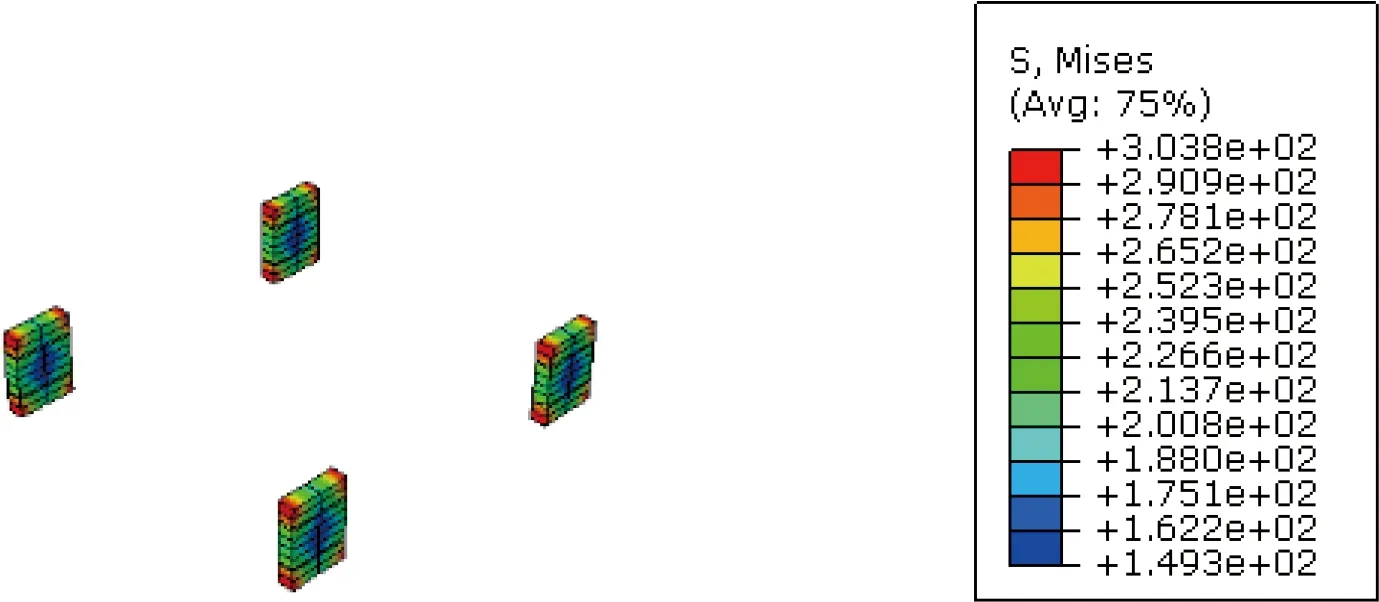
(c) Z-yarns

(a) Inner RUC

(b) Matrix

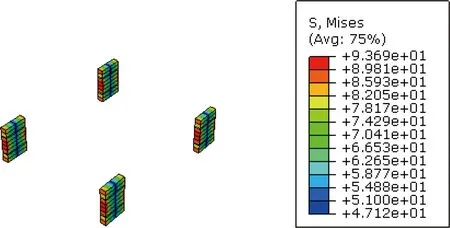
(c) Z-yarns

(a) Surface RUC

(b) Matrix

(a) Surface RUC

(b) Matrix

(c) Z-yarns

(a) Inner RUC

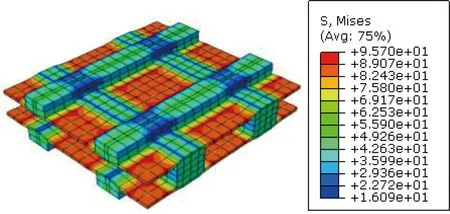
(b) Matrix

(c) Z-yarns

(a) Surface RUC

(b) Matrix

(c) Z-yarns

(a) Surface RU

(b) Matrix

(c) Z-yarns

(a) Surface RU

(b) Matrix

(c) Z-yarns

From the above results for various loading cases, the stress levels in the surface layer are higher than those in the inner layer， which indicates that damages of the 3DOWC may generally initiate from the surface layer. Although fiber yarns are main load carriers， matrix cracking may initiate before the fiber yarn fracture due to lower ultimate strength of matrix， especially near the intersection area of different directional fiber yarns. The introduction of the Z-yarns increases the stiffness in thickness direction and reduces overall matrix stress level in the 3DOWC under the out-of-plane loadings. This explains higher resistance to delamination of the 3DOWC. However， high stress concentration is observed in the L corner of the Z-yarns under the shear loadings. Therefore， fracture of fiber yarns of the 3DOWC is most possibly to start from the Z-yarns at this corner.

3.3 Analysis based on the classic laminate’s theory

In the classical laminate theory， only in-plane mechanical properties of laminated composites are considered. The constitutive relation for the current 3DOWC can be expressed as

(1)

Table 6 In-plane stiffness matrix coefficients of full meso-RUC and sub meso-RUCs

In this case， the whole 3DOWC is seen as a laminate consisting of 14 inner layers and top/bottom surface layers. The in-plane and flexural coefficients are obtained from the following Eq. (2) based on the thicknesses of the sub meso-RUCs listed in Table 3.

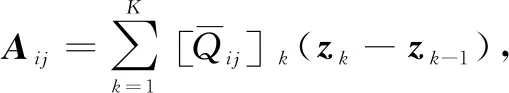
(2)

The in-plane and flexural stiffness coefficients of the 3DOWC depending on the full thickness meso-RUC and based on its sub-meso-RUCs are calculated， respectively， and listed in Table 7 (Aijfor GPa·mm andDijfor GPa·mm3). The results from these two alternative methods are in very good agreement.

Table 7 In-plane and flexural coefficients of full meso-RUC and sub meso-RUCs

4 Conclusions

Elastic mechanical properties of 3DOWC have been predicted based on finite element analysis on micro- and meso-scale RUCs. From the micro-RUC， property of fiber yarn is predicted initially. Then property of the 3DOWC is predicted based on the meso-RUC constructed according to actual architecture of fiber yarns in the 3DOWC. For thick 3DOWCs containing relative large number of plies， an alternative simpler method based on smaller surface meso-RUC and inner meso RUC can be applied. The predicted properties of the 3DOWC by the two methods are in quite good agreement. An important advantage of the proposed methods lies in that not only the global properties of the composite can be predicted but also detailed stress/strain distributions in the fiber， fiber yarns and matrix are provided. This information is helpful in understanding damage/failure mechanisms of the 3DOWC under various loading conditions. It is found that damage of the 3DOWC most possibly initiates from the surface layer where the maximumeffective stress level is generally higher than that in the inner layers. Stitching Z-yarns in the 3DOWC can improve the property in out-of-plane direction； however， the fiber yarn fracture may start from L corner of the Z-yarns due to high stress concentration.