氧化锌电阻阀片中ZnO(002)/β-Bi2O3(210)界面结构的第一性原理研究
李亚莎,黄太焕,谢云龙,徐 程,刘国成
(三峡大学 电气与新能源学院,宜昌 443002)
1 引 言
金属氧化锌避雷器作为电力系统中最基本的保护设备,因其具有优良的非线性伏安特性,它对雷电过电压或操作引起的内部过电压有着重要的限制作用[1]. 由于界面对材料有着非常重要的影响,国内外学者将研究重点集中在晶界处[2]. 国外学者对晶界构建双肖特基势垒模型,该模型认为ZnO陶瓷的晶界区存在着由电子陷阱造成的界面态,这些电子陷阱能够束缚电子形成负电荷层,从而在ZnO晶粒表面造成正空间电荷区,微观解释了氧化锌电阻片的非线性特性[3,4]. 国内学者借助XRD,SEM,电性能测试等手段,对ZnO压敏陶瓷的组成、结构及压敏电阻的性能进行了表征,探讨了工艺参数对压敏电阻性能的影响及其机理[5]. 而Benoit等人运用蒙特卡罗法模拟了Bi2O3在ZnO晶粒表面以及ZnO晶粒间的形成过程,在预熔化模拟过程中,发现位于ZnO晶粒表面及晶界间的Bi2O3相随着预热温度的升高而增厚,这和实验结果吻合,且表面及晶界间的Bi2O3浓度要高于相内[6]. 国内学者测量电阻片在不同温度下的介电频谱,基于电阻片介电特征损耗峰起于耗尽层内本征缺陷电子松弛过程理论,计算了ZnO的本征缺陷结构,并进一步求出了单晶界击穿电压的理论值,该值与外国学者所测量的ZnO-Bi2O3异质结击穿电压范围值2.3 V-3.0 V吻合[7,8]. 在对 ZnO压敏电阻片进行的冲击试验中发现晶界处界面态陷阱主要控制着ZnO压敏电阻片的电气性能和稳定性[9]. 国内学者将纳米ZnO掺入氧化锌压敏电阻中,增加压敏电阻的界面数,有效提高阀片的电位梯度和能量耐受能力[10]. 截至目前,对ZnO/Bi2O3界面结构运用第一性原理进行分析的相关文献还很少. 氧化锌电阻片在烧结过程中,在晶界处会产生不同相的Bi2O3以及焦绿石相和尖晶石相结构[11-13]. 在不同退火温度下,电阻片的非线性系数也会不同[14]. 当ZnO电阻阀片中以β相和δ相Bi2O3为主要成分时,电阻片有着优异的的非线性特性[15, 16]. 本文建立了ZnO/β-Bi2O3界面模型,分析了界面原子的弛豫位移,界面附近的电子结构,界面内形成的内建电场,以及界面能等,为研制高性能ZnO电阻片提供了理论基础.
2 计算方法和模型的建立
CASTEP(Cambridge Serial Total Energy Package)软件包是基于密度泛函理论的从头计算量子力学程序,利用总能量平面波赝势方法,将离子势用赝势代替,电子波函数用平面波基组展开,电子-电子相互作用的交换和相关势由局域密度近似(Local-density approximation, LDA)或广义梯度近似(General gradient approximation, GGA)进行校正,是目前较准确的电子结构计算程序. 本文在GGA框架下,用PBE泛函形式确定交换和相关势,自洽求解Kohn-Sham方程. 采用超软赝势描述价电子与离子实之间相互作用,倒易空间中平面波计算的最大截止能量为380.0 eV,迭代计算时每个原子的总能量收敛设为5.0×10-6eV,每个原子上的受力不大于0.1 eV/nm,公差偏移小于0.00005 nm,应力偏差小于0.02 GPA,自洽迭代次数为300次. 在ZnO电阻片中存在ZnO(002)/β-Bi2O3(210)位向关系的两相界面,构造两相界面结构[17, 18].
在构建界面结构的过程中,晶格匹配是不容忽视的因素. 如果晶格失配度过大,则由于界面应力大结构不稳定. 本文选择了4层ZnO(002)与4层β-Bi2O3(210)作为研究对象. 首先对晶胞进行结构优化,运用GGA处理后获得晶胞参数分别为:ZnO(a=0.32815 nm,c=0.52950 nm);β-Bi2O3(a=0.77169 nm,c=0.5580 nm);然后对优化后的晶胞结构切割,获得指定表面结构,再次进行结构优化后得到ZnO(002),β-Bi2O3(210)表面结构;在此基础上构建界面结构,界面模型用真空层间隔,真空层厚度为1 nm. 模型的建立采取以Zn原子为终端的ZnO表面(以Zn为终端的ZnO表面能小,形成的界面较O为终端的稳定性好,故选取以Zn为终端的ZnO表面比较符合实际情况).
3 结果与讨论
3.1 界面微观结构
以ZnO(002)/β-Bi2O3(210)界面结构模型为研究对象,图1中红色球表示O原子,紫色球表示Bi原子,灰色球表示Zn原子. 图1(a)为构建的ZnO(002)/β-Bi2O3(210)界面结构主视图;在图1(a)中,一条贯穿β-Bi2O3中O原子,Zn1层原子,O1层原子的实线为后续用于差分电荷密度分析时所取得的切割面位置. 图1(b)为界面结构仰视图. 如表1可知,晶格失配度分别为1.00%,0.60%,失配度较小,符合界面构造规律. 与此同时,在ZnO(002)层片结构中,界面轴方向Zn-O键平均键长为0.2000 nm,其它方向Zn-O键平均键长为0.1995 nm;在β-Bi2O3(210)层片结构中,Bi-O键平均键长为0.2371 nm. 在ZnO(002)/β-Bi2O3(210)界面结构中,界面轴方向Zn-O键平均键长为0.2126 nm,其它方向Zn-O键平均键长为0.1939 nm,Bi-O键平均键长为0.2340 nm. 由于靠近界面侧ZnO层片和β-Bi2O3层片内的原子没有近邻原子从而存在悬挂键,这使得界面和界面附近原子在满足上述收敛条件下,为了使界面两侧未完全配对的表面原子受力得到平衡,界面内的原子的位置发生弛豫,弛豫后原子达到新的平衡位置,界面处的悬挂键得到部分饱和. 因此,ZnO(002)/β-Bi2O3(210)界面结构中原子间的键长同ZnO(002)层片结构和β-Bi2O3(210)层片结构的键长相比发生了改变.
弛豫后的结构实质上是两相的一种过渡区,没有发生相原子结构的突变,符合界面结构构造规律. 当界面处原子的位置发生弛豫,原子间的电荷发生转移,影响材料的性质[19].
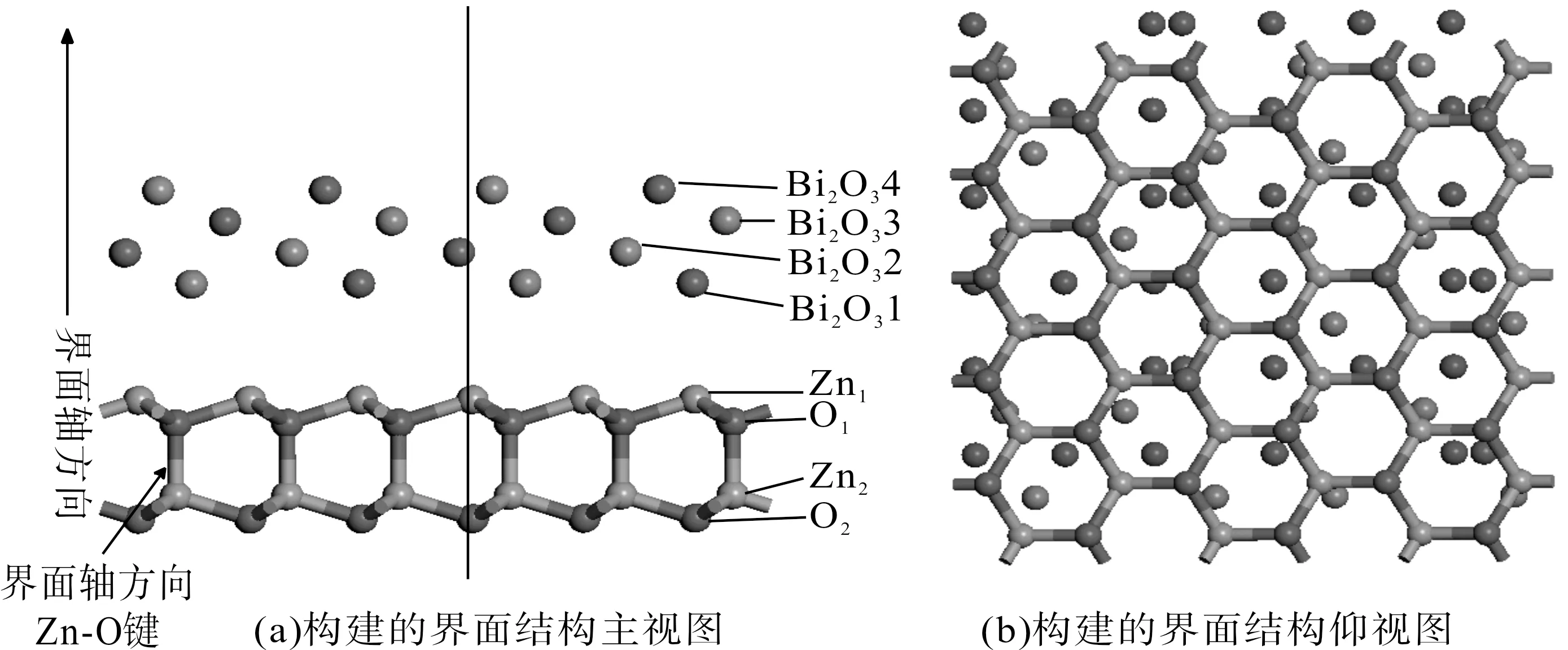
图1 ZnO(002)/ β-Bi2O3(210) 界面结构模型Fig. 1 The modeling of ZnO(002)/ β-Bi2O3(210) interface structure
Table. 1 The two-dimensional lattice constants of ZnO(002)/β-Bi2O3(210) interface structure and the bond length in different systerm were caculated
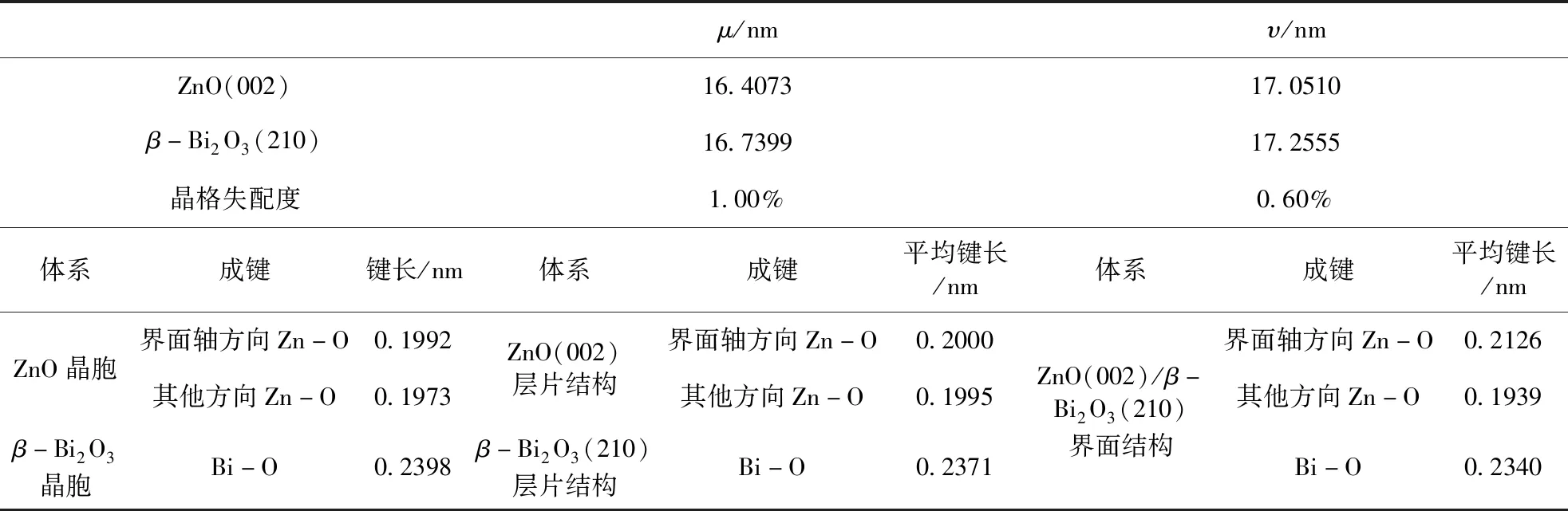
μ/nmυ/nmZnO(002)16.407317.0510β-Bi2O3(210)16.739917.2555晶格失配度1.00%0.60%体系成键键长/nm体系成键平均键长/nm体系成键平均键长/nmZnO晶胞β-Bi2O3晶胞界面轴方向Zn-O0.1992其他方向Zn-O0.1973Bi-O0.2398ZnO(002)层片结构β-Bi2O3(210)层片结构界面轴方向Zn-O0.2000其他方向Zn-O0.1995Bi-O0.2371ZnO(002)/β-Bi2O3(210)界面结构界面轴方向Zn-O0.2126其他方向Zn-O0.1939Bi-O0.2340
3.2 界面差分电荷密度图、原子的电子布居及内建电场
图2为计算得到的差分电荷密度图,可以直观地显示由于ZnO层片和β-Bi2O3层片的相互作用对界面结构中原子的电子分布影响. 图2是图1所示切割面上的差分电荷密度图. 蓝色表示电子的缺失,红色表示电子的获得. 可以看出在同一平面内O原子周围电子的局域性分布明显,显示较强的离子键. ZnO层片中的Zn原子与β-Bi2O3层片中的O原子间存在电荷转移,Zn原子周围出现电荷缺失区,O原子周围出现电荷富集区,这说明由于界面结构的存在,β-Bi2O3层片中的O原子从Zn层片中的Zn原子获得电荷.

图2 差分电荷密度图Fig. 2 Charge density difference illustration
界面附近原子的电子分布变化可由Mulliken布居分布定性获得,表2为界面处原子轨道的电子转移情况,可以看出Zn原子随偏离晶界距离不同失去的电子数有别,Zn1原子中自由度相对最大的s态电子数为0.50,Zn2原子的s态电子数为0.61,两者存在0.11的差别,Zn1、Zn2原子的p、d态电子数几乎一样. ZnO层片中O1、O2原子的轨道电子变化甚小,两原子的p、d态电子数仅有0.01的差别. 由此说明,Zn1和O1原子所构成的第一层原子所带正电荷量要大于Zn2和O2原子构成的第二层原子所带正电荷量. Bi2O31层中Bi原子中s态电子数为1.88,Bi2O32层中Bi原子中s态电子数为1.75,两者存在0.12的差别. 前者原子p态电子数为2.08,后者原子p态电子数为1.72,两者相差0.36.β-Bi2O3层片中1、2层O原子的轨道电子变化不大[20, 21]. 同理可得Bi2O31层所带的负电荷量要大于Bi2O32层所带负电荷量. 因此,越靠近晶界,两侧的层片电荷交换越剧烈. 通过计算晶界结构中ZnO层片与β-Bi2O3层片所带的总电量,发现ZnO层片带正电23.61e,β-Bi2O3层片带负电23.64 e,两者存在微小误差,这也从侧面验证了空间电荷计算的准确性. 因此在ZnO(002)/β-Bi2O3(210)界面结构中形成了由ZnO层片指向β-Bi2O3层片的电场.
通过密度泛函理论计算得到界面结构沿着界面轴方向的静电势曲线图,如图3所示,由于界面结构两侧的ZnO和β-Bi2O3结构不同,静电势沿界面方向发生了突变. 位于左上方类似正弦函数曲线为ZnO层片静电势图,位于右下方类似正弦曲线为β-Bi2O3层片静电势图,图中横坐标为界面结构沿界面轴方向的区间长度. 可以看出ZnO层片的平均电势高于β-Bi2O3层片的平均电势,因此进一步说明在界面结构内存在一个内建电场由ZnO层片指向β-Bi2O3层片[22]. 内建电场是材料呈现非线性伏安特性的重要原因[23, 24].
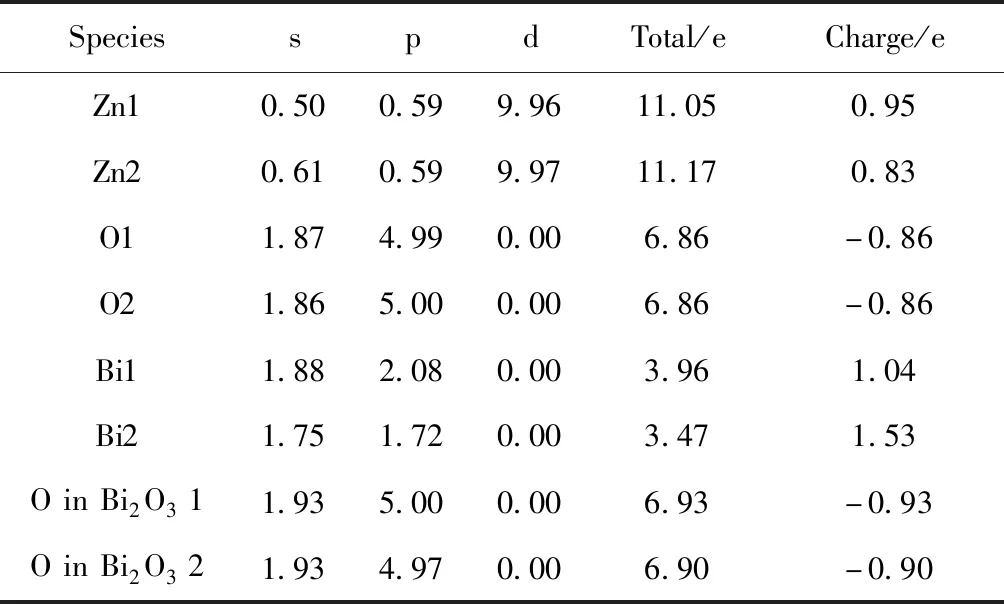
表2 不同原子的电子布居
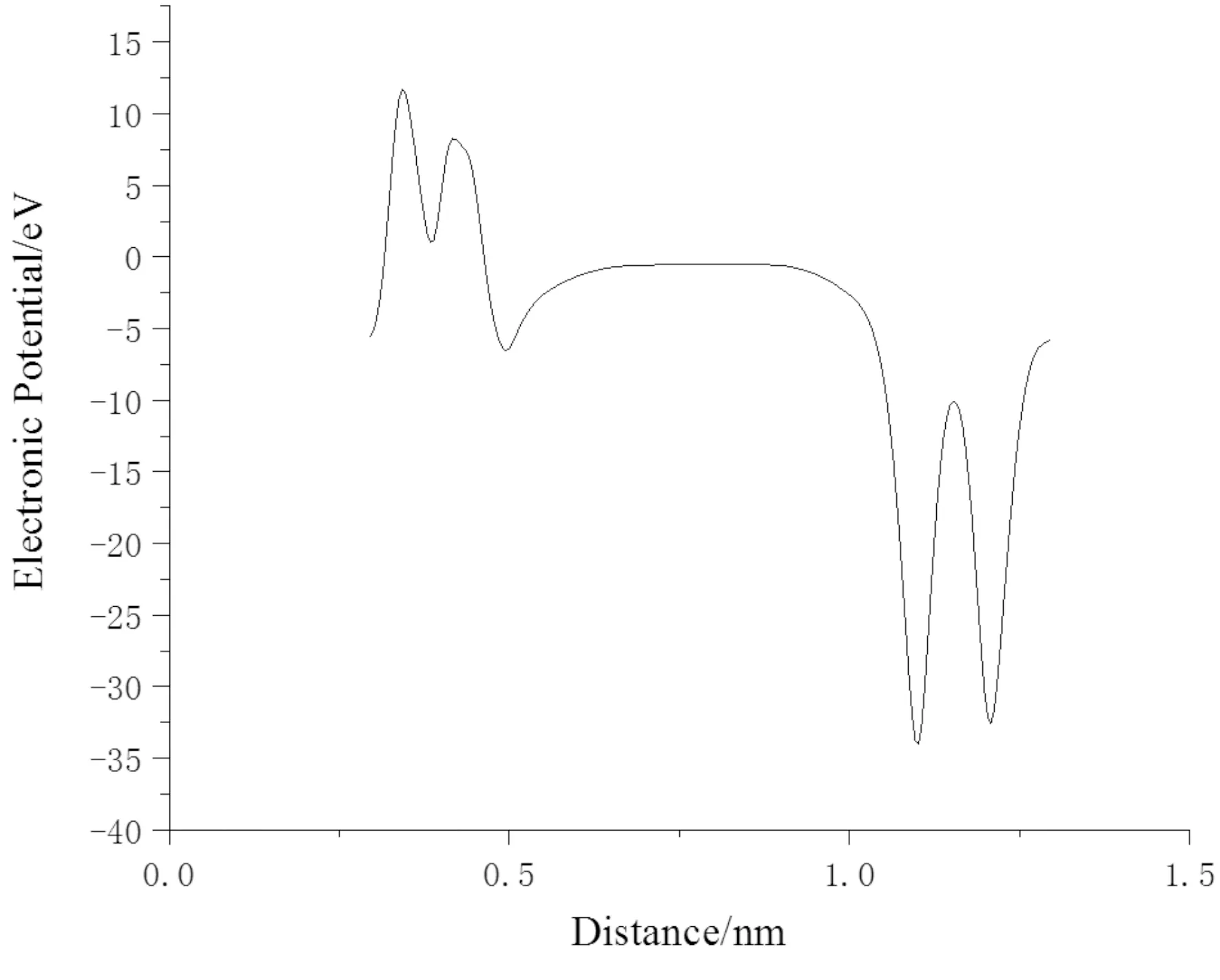
图3 沿界面轴方向的静电势图Fig. 3 Electrostatic potential along the interfacial normal direction
究其根本原因,ZnO和β-Bi2O3两种组分的费米能级和真空能级位置不同,两者构成界面结构后,其价带和导带的带边位置也会随之改变,两者的功函数也存在差异,驱动自由电子在ZnO和β-Bi2O3间转移,ZnO的功函数小于β-Bi2O3功函数,电子从ZnO层片转移至β-Bi2O3层片,直至两者的费米能级对准. 由于整个材料是电中性的,界面处的电子必然会在材料内部形成许多微小的电势场,这些内部形成的电势场是形成氧化锌电阻片非线性伏安特性的重要原因[19].
3.3 界面区态密度
图4绘制了原子分波态密度图,由界面总态密度及原子分波态密度图4(a)知,位于-16.57 eV~-21.15 eV的下价带区出现了局域峰,其宽度较窄,局域性较强,属于深能级处的轨道相互作用,其主要是由O的2s轨道贡献. 在-0.94 eV~-3.91 eV和-5.11 eV~-8.42 eV能量区域存在两个高密度的态分布. 在-5.11 eV~-8.42 eV能量区域内价带电子态密度分布的主极大和次级大分别位于-5.80 eV和-6.44 eV附近. 电子在该区域有一定局域性,该区域主要由O的2p轨道和Zn的3d轨道贡献,且在重叠区域,高低能部分的态密度分布情况相反,也就是说态密度产生“共振”现象,这说明该区域存在p-d轨道的杂化效应,形成较强键态. 在-8.45 eV~-12.36 eV区域主要由O的2p轨道和Bi的6s轨道贡献,该区域存在s-p轨道杂化.

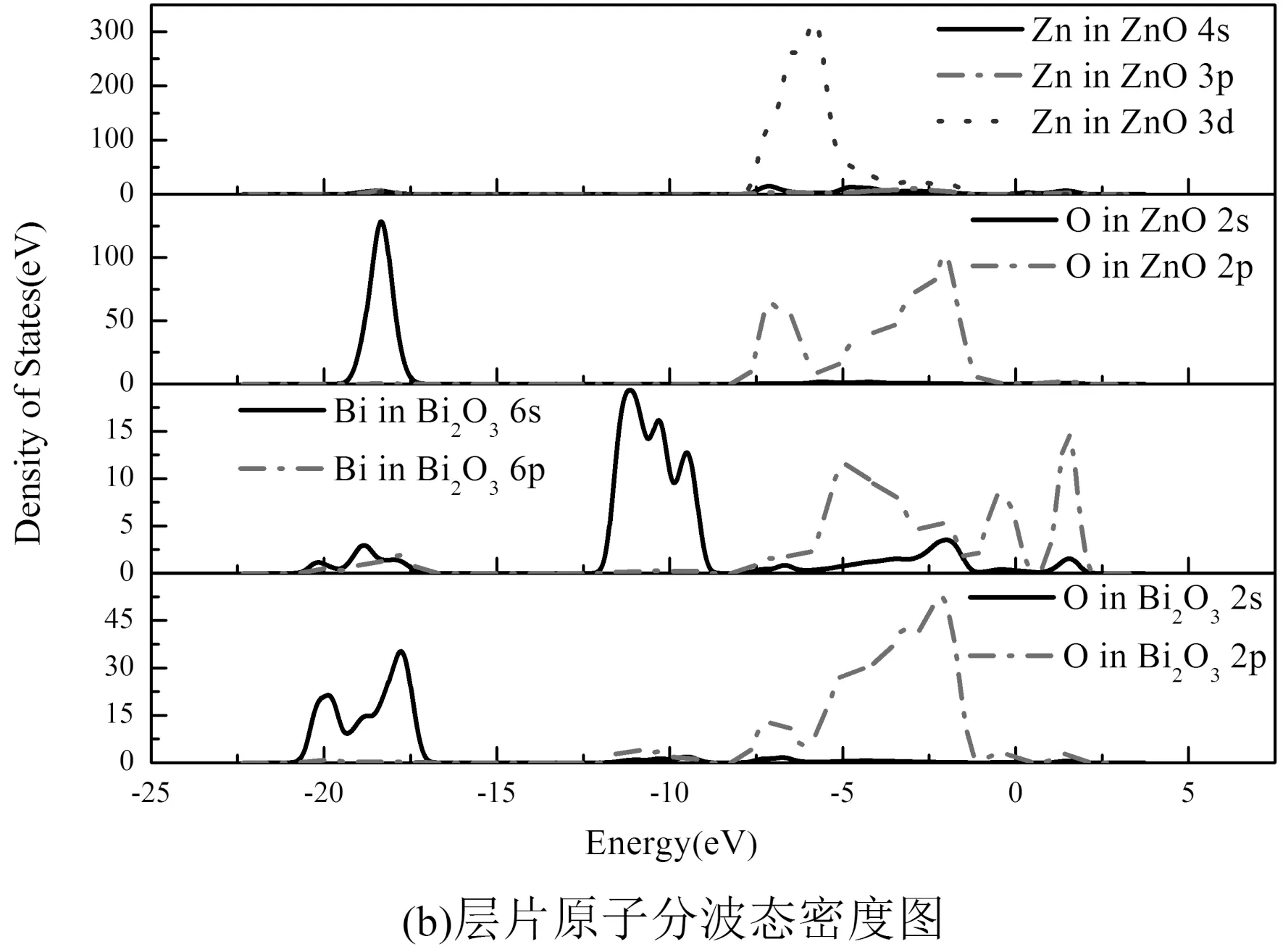
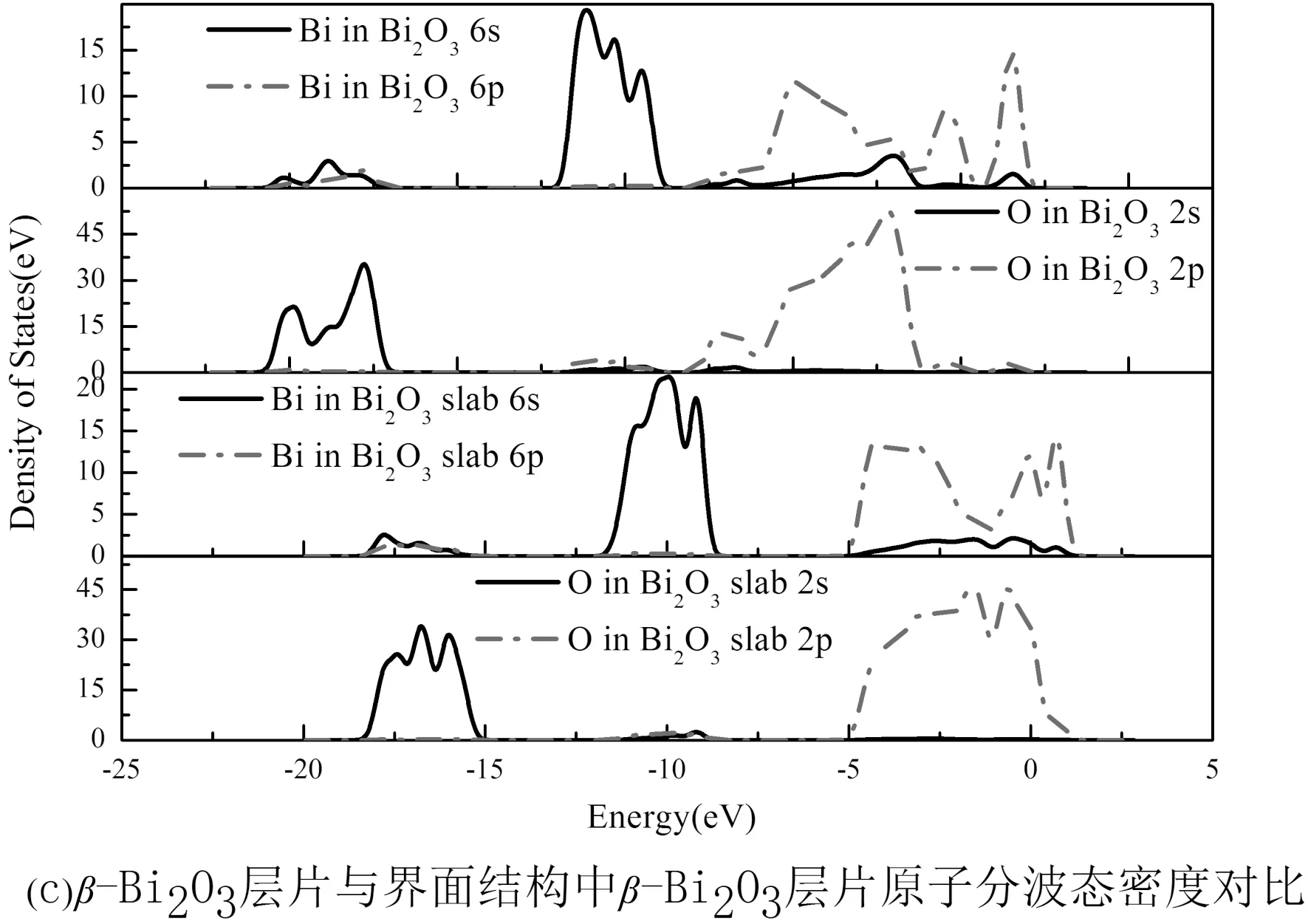
图4 界面原子分波态密度图Fig. 4 Partial densities of states of the interface atoms
由层片原子分波态密度图4(b)知,界面ZnO侧的Zn原子的3d价电子与β-Bi2O3侧的O原子的2p价电子的分波态密度图在低能量区产生较好重合,且在重叠区域,态密度分布也产生“共振”现象,这说明界面侧的Zn原子与O原子间产生相互作用并结合成键. 图2-b还显示ZnO侧的O原子与β-Bi2O3侧的Bi原子也存在小范围的重叠,但是重叠峰值较弱,说明ZnO侧的O原子与β-Bi2O3侧的Bi原子间存在相互作用但是较弱.
由于Zn原子为β-Bi2O3侧的O原子提供了电荷,界面附近的Bi原子束缚减弱,由纯β-Bi2O3层片与ZnO(002)/β-Bi2O3(210)界面结构中的β-Bi2O3层片原子分波态密度对比图4(c)知,对比β-Bi2O3(210)表面的O原子,Bi原子与弛豫后界面β-Bi2O3侧的O原子,Bi原子态密度图可知,界面附近的Bi原子6p轨道较活跃,非局域性增强,同时界面结构中O原子,Bi原子态密度图中的一个谱峰向低能量区移动,与另一个谱峰靠近[25, 26],这说明界面中β-Bi2O3层片内O原子与Bi原子之间成键减弱.
3.4 界面能
界面区的微结构、界面结合强度对材料的宏观性能起着重要的作用. 界面能是两个自由表面结合形成单位面积的稳定界面所需能量,反映了自由表面结合形成界面过程中能量的释放,能量代数值越小越稳定,即意味着形成界面过程中释放的能量越大,结合就越稳定[27]. 界面能定义为:
(1)
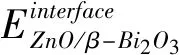
4 结 论
本文构造了ZnO/β-Bi2O3界面结构,采用第一性原理分析了界面原子的弛豫,界面附近的电子结构,界面内形成的内建电场,以及界面能等,分析表明:
(1)由于ZnO(002)/β-Bi2O3(210)界面结构中存在悬挂键,弛豫后会引起界面原子的混排,破坏界面原子的周期性排列;界面结构中原子间的键长相对于独立层片中的原子间的键长发生改变. 界面是材料系统降低能量的一种方式,弛豫得到的界面结构是一种两相结合的过渡区.
(2)界面区二次差分电荷密度图及原子布居分析表明,在ZnO(002)/β-Bi2O3(210)界面结构中,ZnO层片中Zn原子电荷缺失,β-Bi2O3层片中O原子电荷富集,ZnO层片向β-Bi2O3层片转移电子电荷23.61e. 通过做出沿着界面轴方向的静电势图,晶界两侧层片存在电子势能差,进一步说明了晶界结构内存在内建电场. 内建电场是材料非线性伏安特性的原因.
(3)界面的结合主要依靠ZnO层片中Zn原子与β-Bi2O3层片中O原子相互作用. ZnO层片中的O原子2p轨道与Bi2O3层片中的Bi原子6s轨道也存在杂化. 相对于β-Bi2O3块体,界面结构中的β-Bi2O3层片中Bi原子非局域性增强,Bi、O原子间成键减弱.
(4)计算发现ZnO(002)/β-Bi2O3(210)界面能约为-4.203 J/m2,界面结合过程释放能量,界面结合较稳定.
——以内蒙古伊敏煤为例

