基于STP的零部件关系网简单路径搜索方法研究
魏美华,刘小龙,延卫军
(1.榆林学院 数学与统计学院,榆林 719000;2.榆林学院 管理学院,榆林 719000)
0 引言
制造业零部件的关系网、物联网、运输流、电网等共同的载体就是网络,如交通流、管道输送等涉及到有向无环网络,任何一个网络都可以用图论来刻画。在实际问题中,最短路径不一定是最优的路径[1],但最优路径应该是无障碍的。从而寻找图的简单路径[2]具有一定的实际意义和应用前景,例如应用于通信系统[3]、生物信息学[4]等领域中。
面对大批量定制,企业所制造的零部件种类多和数量大,零部件间存在着庞杂的隶属关系。一个备受关注的问题就是零部件的总用量和零部件的总使用次数。为了满足某零部件的总用量,有必要计算从产品族中的所有产品出发到该零部件的所有简单路径,然后计将该零部件的所有简单路径的用量累加,得出该零部件在产品族中的总用量[5]。将产品族零部件视为网络中的节点,零部件间的隶属关系视为网络中的有向边,表示上一级部件指向直接隶属于该零部件的下一级零部件,这样产品族零部件关系网络就构成一个有向无环图。
上述问题涉及到寻找有向图的简单路径.而列举所有的简单路径和环是图论中的NP难问题[6]。受文献[7]启发,本文基于矩阵半张量积(STP)理论[8,9],通过定义邻接矩阵,建立了简单路径和环的模型,采用矩阵方法约化搜索空间,并结合代数方法精确寻找有向图的简单路径和环,得到一个新的搜索算法,并对该算法进行验证。
1 模型建立和分析
给定有向图G=(V,E),顶点集V={v1,v2,…,vn},边集E={e1,e2,…,em},它的邻接矩阵为A=(aij),其中元素aij=1当且仅当从顶点vi到顶点vj有一条有向边,否则aij=0。简单路径(环)就是没有重复顶点的路径(环)。s为简单路径(环)就是具有s个顶点的简单路径(环),例如图1表示5-简单有向路径。

图1 5-简单有向路径的连接关系
模型1 设点集V1V,V1=,i1,i2,…,is{1,2,…,n},5≤s≤n。顶点导出有向子图G(V1)是s-简单路径当且仅当
1)AV1中一个元素为0,其余元素为1。这里:
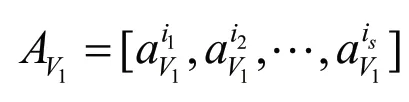
2)若iσ≠iτ时,则jτ≠jσ。
3)V1的任意子集满足:

其中:
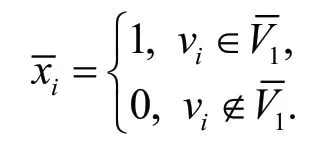
注1:当s≤2时,s为简单路径和环意义不大。当s=3,4时,顶点导出有向子图G(V1)是s为简单路径当且仅当模型1中的(i)和(ii)成立。

其中:

2)若当iσ≠iτ时,则jτ≠jσ。
3)V1的任意子集满足:

其中:

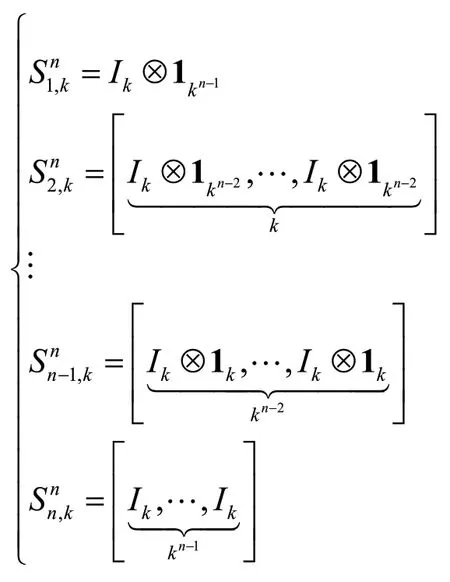
注2:当2 矩阵半张量积是矩阵普通乘积的一个推广,其不同于矩阵的普通乘积,不要求前一个矩阵的列数与后一个矩阵的行数相等,然而它却保持着矩阵的普通乘积的基本性质。 给定有向图G=(V,E),其中顶点集V={v1,v2,…,vn},边集E={e1,e2,…,em},它的邻接矩阵为A=(aij),其中矩阵中的元素aij=1当且仅当从顶点vi到顶点vj有一条有向边,否则aij=0。算法的基本原理如下: 根据上述基本原理,按照下列步骤寻找有向图的所有的或任意指定长度的s为简单路径和环。 步骤2:利用J=[1,0]提取MV1的第一行,并记为β=JMV1=[b1,b2,…,b2n]。若bi≠s-1,i=1,2,…,2n,则图G没有s为简单路径,计算终止.否则向量β中元素s-1的列标分别记为r1,r2,…,rp。 步骤3:对于每一个rj,j=1,2,…,p,其对应于。根据文献[4],令: 步骤4:检验上述含有s个顶点的S(rj)是否满足模型1的条件。符合条件的子图S(rj)构成所有的s为简单路径。 注3 结合模型2类似可寻找简单环的算法。 设有向图G=(V,E)如图2所示,并借助MATLAB软件进行搜索寻找任意给定长度的简单路径和环,以寻找8-简单路径为例,以此验证算法的有效性。 图2 有向图的连接关系 有向图2的邻接矩阵为: 根据算法步骤1易得MV1,并利用J=[1,1]提取第一行,则该行元素是7的列标为r1,r2,…,r345,这是所有可能形成简单路径的元素。 根据算法的步骤3可知,元素个数是8的S(rj)仅有25个,根据步骤4对于复杂的有向图2只有一条8-简单路径,如表1所示。 表1 图2的8-简单有向路径 制造业中产品族零部件关系网络中,企业所关注的零建立部件的总用量和零部件的总使用次数,这涉及到有向图的简单路径搜索问题。本文建立了简单路径和环的模型,通过邻接矩阵,运用矩阵半张量积理论,得到了寻找有向图所有的或任意给定长度的简单路径和环的新算法,运用该算法减少了搜索空间的范围,并能精确寻找有向图的指定长度或所有的简单路径和环。该算法对于企业零部件关系网的简单路径搜索问题有一定的参考价值。2 基于STP的搜索算法

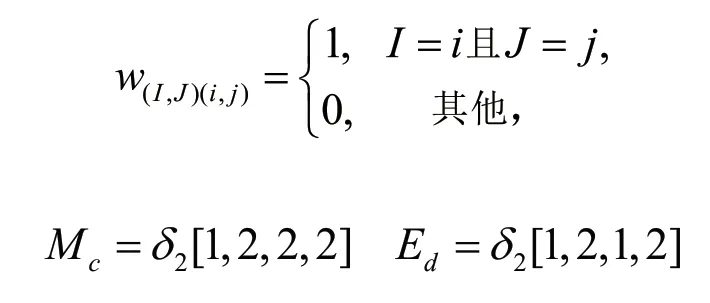
3 算法实例验证



4 结论

