基于Milk-Run的多供应商物料配送策略研究
程攀攀,杨晓英
(河南科技大学 机电工程学院,洛阳 471003)
0 引言
随着农业现代化和生产集约化的推进,农业生产各领域在加快推进“机器换人”,促进农机行业正在向全程化、大型化、智能化转变,对农业机械化供给侧的能力、质量和效率提出了新的更高的要求。如何顺应新形势新需求,以创新发展为驱动,快速响应市场需求,提供客户满意的产品与服务,在市场中取得竞争优势,成为我国农机制造企业生存和发展面临的重要问题。供应商是企业获得竞争力的重要资源,供应商物料配送的准时化和标准化不足问题一直是制约农机企业生产的瓶颈,供应商物料配送如何与制造企业生产协同成为企业快速响应市场需求的关键。因此研究面向农机制造的供应商协同物料配送策略,对提升农业供给侧能力和建设现代农业具有重要的意义。
国内外学者已经对供应商准时化物料配送进行了深入研究。Droste M等[1]强调了为了应对制造企业的发展趋势,企业必须做好循环取货模式下的入厂物流这一复杂且重要的系统。Wang L等[2]研究了循环取货模式实施的条件和原则,在装载率最大化的基础上构建模型实现运输费用最短。Emde S等[3]利用JIT原则实现物料准时配送,以配送距离、配送时间安排约束求解物料的配送周期、配送批次。Cao Z[4]和Boysen N等[5]以最小化留存成本和配送成本为目标,建立数学规划模型,提出了物料网监控和顺序供应准时化配送策略。YQ Rao等[6]通过准确的设计配送车辆的路径、物料数量和配送时间,降低线边库存和运输成本。关旭[7]分别建立了单供应商对单制造商和多供应商对单制造商的主从博弈准时供货模型,确定了供应商的最优供货时间决策和制造商最优的库存责任期设置。金光等对丰田企业中厂内和场外物流模式进行分析,确定了供应商的精益物流模式[8,9]。王东方等[10]从循环取货的车辆路径设计、流程设计等方面对远距离零部件供应商循环取货进行系统的研究。针对Dijkstra算法求解最优路径问题,蔡惊涛[11]、陈亚琳等[12]为解决物流运输中的最短路径优化问题,运用改进Dijkstra算法通过动态调整权值实现不同要求最佳路径选择。刘坤华等[13]以最大完工时间最小为目标,运用改进Dijkstra算法对其进行求解。王树西等[14]分析了多邻接点问题与多条最短路径问题的成因,提出解决方案,对Dijkstra算法进行了改进。
以上研究从供应商物流模式选择、供应商循环取货路径规划与选择做出了很大贡献,对于研究供应商物料配送具有重要借鉴意义,但是对于多供应商循环取货模式下物料配送期量标准模型研究较少。为此,本文针对多供应商物料配送特征,提出了基于Milk-Run的供应商物料配送模式,建立数学规划模型,并采用双层规划法确定各供应商循环路径及物料配送期量,提高供应商物料配送的精准率。
1 问题分析
1.1 传统模式分析
供应商物料配送问题可以看作是由一个核心制造商、多个供应商所组成的供应链系统,精准化的供应链是供应商必须按照生产顺序计划需求准时准量配送物料至制造商,避免高库存和缺货停线。制造商针对一些体积较大或不易分拣的物料采取供应商直接供应至生产线边的方式,供应商直接配送是实现准时化物流的一种重要途径,对供应商的要求较高,且多个供应商同时直接配送多种物料时极易导致配送混乱。一旦发生计划调整,物料配送却没有停止,源源不断的零部件就会到达生产线边,从而造成零部件积压导致成本浪费。循环取货作为准时化物流的一种重要模式,可以实现多频次、小批量的供应商直接配送。因此本文针对一个农机制造商、多个供应商的物料配送问题,提出了基于Milk-Run的供应商准时化物料配送模式。
1.2 基于Milk-Run的多供应商物料配送模式
基于Milk-Run的供应商准时化物料配送模式是由供应商、制造商、运输车辆构成的系统结构,运用JIT思想实现多频次、小批量齐套性供货,如图1所示。这种模式要求供应商、制造商之间信息共享,制造商将生产顺序计划及时传递给各供应商,供应商按照生产顺序备货。在每个循环周期内,运输车辆按照规定路线遍历每个供应商将物料配送至生产线边,多家供应商的各种零部件混装运输,减少供货量较少的零部件单独装车运输造成的配送成本。

图1 基于Milk-Run的供应商准时化物料配送模式
2 基于Milk-Run的供应商准时化物料配送模型
优化目标:由一个制造商、多个供应商的循环取货物流系统中,制造商对于每一种物料库存维持费用,物料配送的周期越短制造商的库存维持费用越低,每条路线运输车辆的装载率越高,需要的运输次数越少运输成本越小。各循环路径配送距离越短越有利于提高配送效率。因此,以供应商运输成本和制造商库存维持成本最小和循环路径距离最短为目标建立多目标数学规划模型。
符号说明:
dij表示由供应商i到供应商j的运输距离,i≠j;
xij=1表示由供应商i到供应商j取货,否则xij=0;
αi表示供应商i提前到达的单位库存维持成本;
Ti表示供应商i的配送周期;
ti表示供应商的实际到达时间;
i=0表示制造商;
L={1,2,…,ι}表示循环路线;
η表示运输车辆的最低装载率;
Q表示运输车辆的最大运载量;
qi表示供应商i的单次运输量。
基于Milk-Run的供应商准时化物料配送模型如下所示。
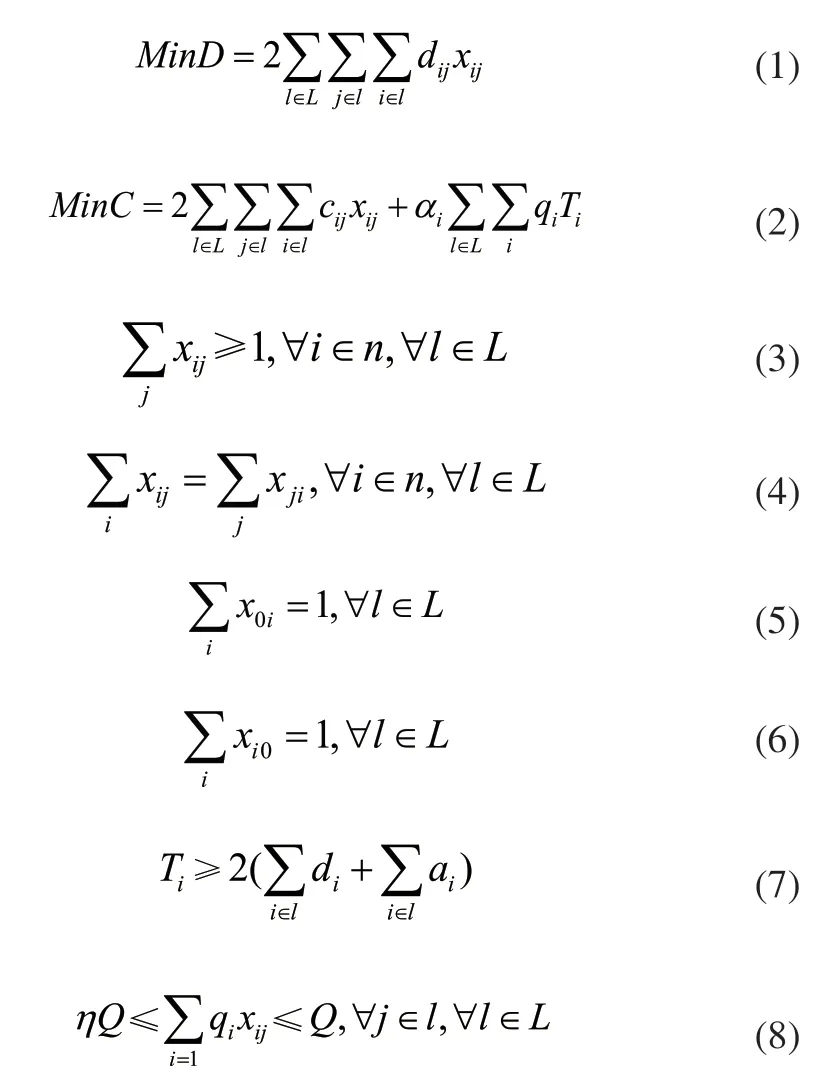
式(1)和式(2)表示目标函数,包括循环路径总距离,供应商的运输成本以及制造商的库存维持成本,以及,式(3)表示每一个供应商都被遍历,式(4)表示车辆在每个供应商取货完成后离开,式(5)和式(6)表示每条路线的起点和终点相同,式(7)表示供应商的到达时间约束,式(8)表示每辆的单次运载量约束。
3 模型求解
基于Milk-Run的供应商准时化物料配送模型是一类复杂多项式数学规划问题,使得模型求解变得十分复杂,因此本文采用双层规划法进行模型求解,上层采用改进Dijkstra算法求解供应商循环取货路径,下层采用订单均衡化处理确定各供应商配送期量,上下层分层迭代保证模型最优解。
3.1 上层最优循环取货路径求解
Dijkstra算法是一种有效解决最短路径问题的经典算法,适用于单源最短路径规划问题,即从一个点开始到所有其他点的路径。Dijkstra算法的基本原理:每次扩展一个新点(该新点到起始点距离为最短),然后计算该新点到其相邻各点的距离。本文构造了改进Dijkstra算法以有效解决循环取货路径规划问题,运用Dijkstra算法拓展新节点的原理,在算法设计中开发并行算子,多节点同时寻找最优路径,加快算法收敛性以及实际操作性。
1)初始化。对所有供应商进行编号,建立四个集合x={0,1,2,3,…,n}表示供应商的点集合,{y}=0表示每条路径的节点集合,即每条路径都是从制造商开始,为路径l的下一个未知节点m=0,z={1,2,3,…,n}表示还未确定路径的供应商集合,任意路径表示为l={0,…,0},即从制造商出发返回到制造商,L={L1,L2,…,Lv}表示路径集合。
2)有向图矩阵。各供应商之间的路径距离是路径规划的决策变量,采用合理化的运输就是以最短距离保证最少的运输次数在合理的时间将物料配送至目的地。构建各节点之间的路径权重因子θ,θ为运输距离矩阵,各个供应商之间都有对应的决策量,则各个节点的有向图矩阵如下:
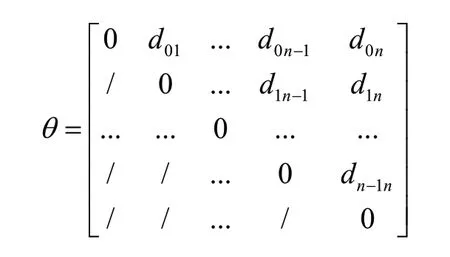
3)计算最优循环路径。使各节点之间的运输路径作为决策因子,每条循环路径由指定运输车辆负责,根据运输车辆数量选取第一节点个数,不同路径在选取第一节点后并行寻找下一节点,直到遍历所有节点停止迭代,否则返回。
1)制造商作为初始变量y0=0。
4)确定每条路径L={L1,L2,…,Ll},直到z=φ。
3.2 下层最优物料配送期量求解
订单平准化的原则就是循环路径的实际情况,按一定标准对货物进行分割,使得每个供应商处所取货量都能在一定时间内满足生产需求,并且尽可能实现零库存,当然也不能出现缺少生产材料现象。订单均衡化在保证配送成本最小的情况下通常与制造商的生产节拍、配送周期内能满足的生产需求为基准,将每日的采购订单进行分割。为了保证运输车辆每次取货一致,同一路径的配送周期相同,在保证成本最低的条件下根据每条路径的运输时间确定配送期量。
1)各供应商的配送周期等于所在路径的运输时间,即Ti=Tl;各供应商的单次配送量为qi=[Qi/Ti]+;各供应商的配送次数按照每天8小时工作均衡配送ti=[8×60/Ti]+;计算制造商库存成本C0。
2)配送次数减少会降低配送成本,但是会增加库存成本,根据利益悖反原则使供应商配送次数逐渐减少,即ti=ti-1,配送期量也随之变化,在此计算制造商库存成本C1。
3)迭代次数设为5次,比较每次成本,选取成本最低的一次作为最优解。
4 实例应用
以某拖拉机制造企业为例,生产节拍为3min/台,每天工作8小时。选取15家直接配送的供应商,编号分别为1,2,…,15,每个供应商日需求量如表1所示。供应商采取循环取货的方式,每辆运输车辆负责一条路径,每辆车的最大运载量为2000kg,每条路径的运输车辆的装载率为75%~100%。

表1 各供应商日需求量
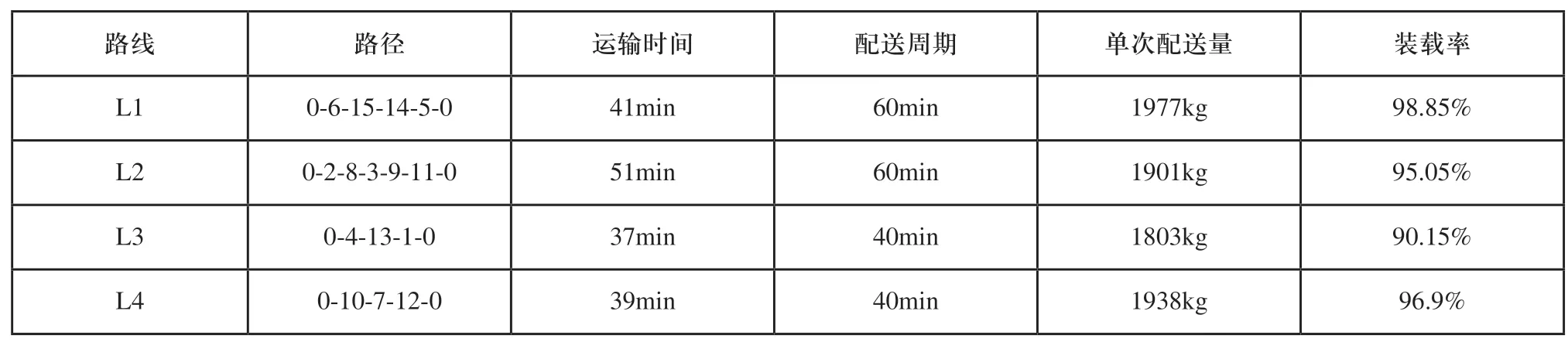
表2 计算结果表

表3 各供应商配送期量表
供应商运输距离矩阵如下所示。

根据上述条件,运用改进Dijkstra算法进行求解,当总成本为11181.6时,取得最优结果,计算结果如下表2所示。
各供应商的配送间隔期及配送量如表3所示。
对比表2和表3可知,采用循环取货物流模式情况下,供应链的总成本最低为11181.6,共有4条循环路线,每条循环路线中运输车辆的运载率分别为98.85%、95.05%、90.15%、96.9%,有效提高了运输车辆的配送效率降低了供应商配送成本。每条路径分别计算了配送间隔期和单次配送量,作业人员只需要按照规定时间到指定供应商选取相应的物料配送至生产线边,实现了物流作业标准化、准时化配送。
5 结论
本文以农机制造的供应商物料配送特征为基础,提出了基于Milk-Run的供应商准时化物料配送模式,提出了供应商订单均衡化处理方法,实现了均匀台套式物料配送,以供应商配送成本及制造商的库存维持成本最小化为目标建立了数学规划模型,实现物料均衡、准时配送,能够避免制造商的缺货停线损失和供应商的配送成本,使供应链利益最大化。运用双层规划法对模型进行求解,上层改进了Dijkstra算法确定循环路径,下层根据循环路径迭代确定各路径的物料配送期量,为供应商的配送方案提供了量化标准,提高了供应商的配送效率,简化了供应商和制造商的物流流程,对实现供应商准时化物料配送具有重要意义。

