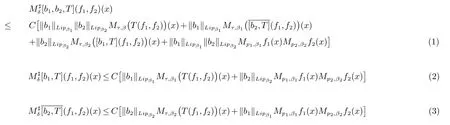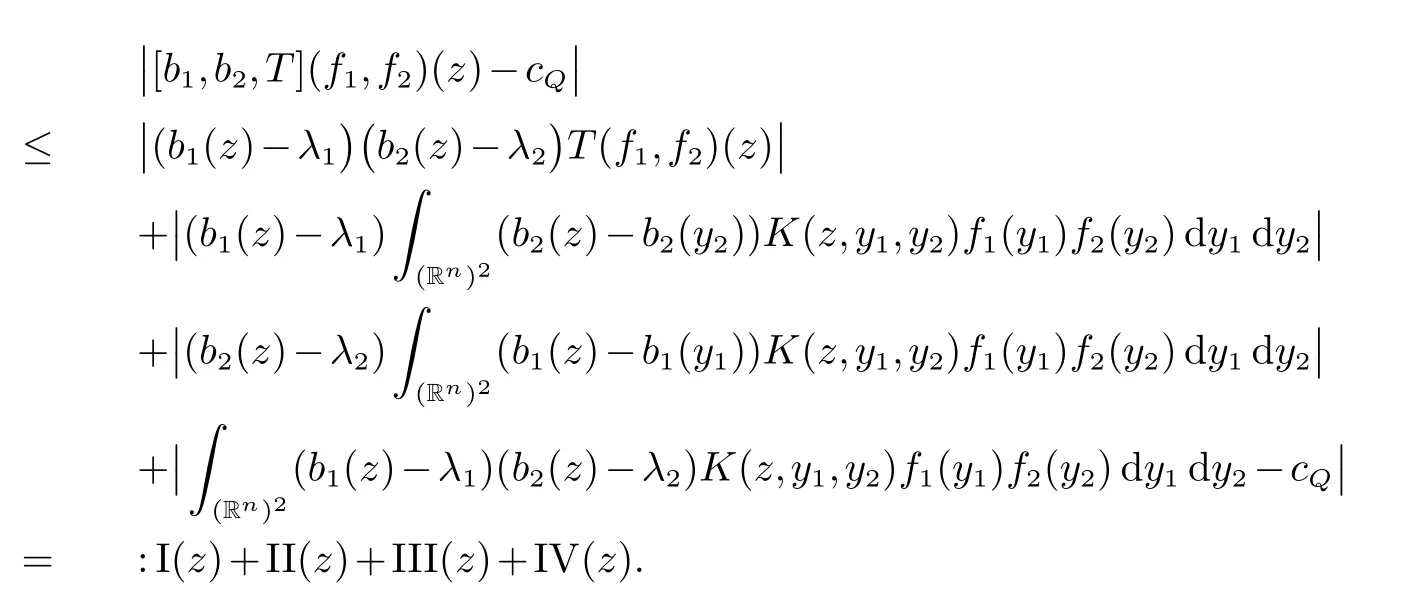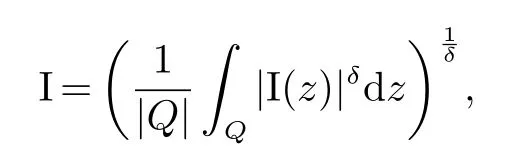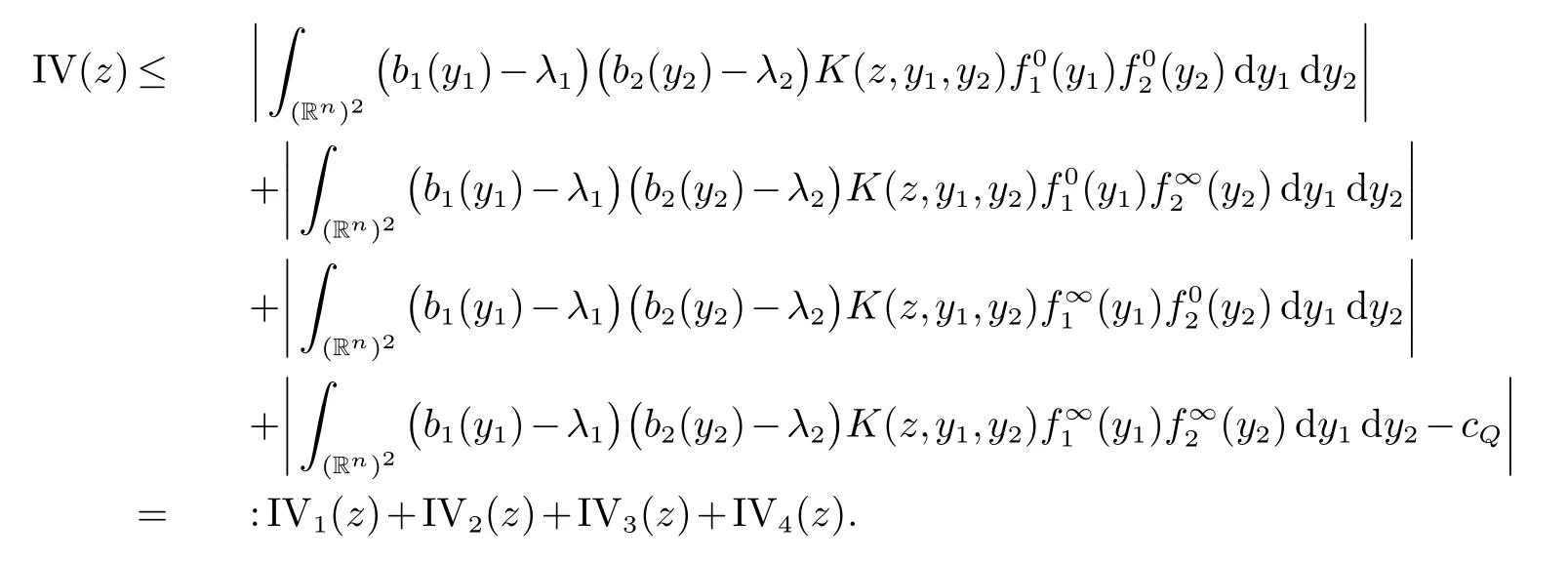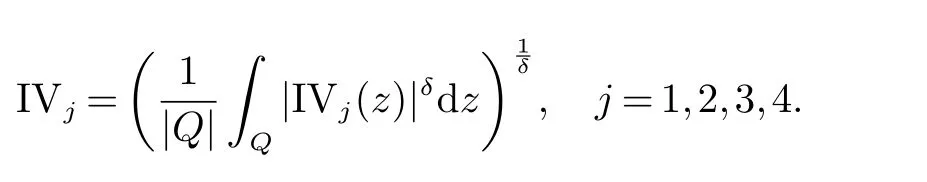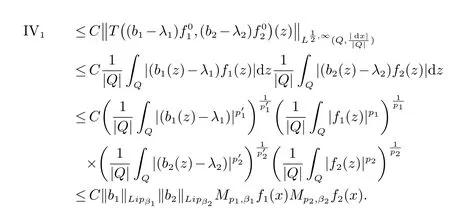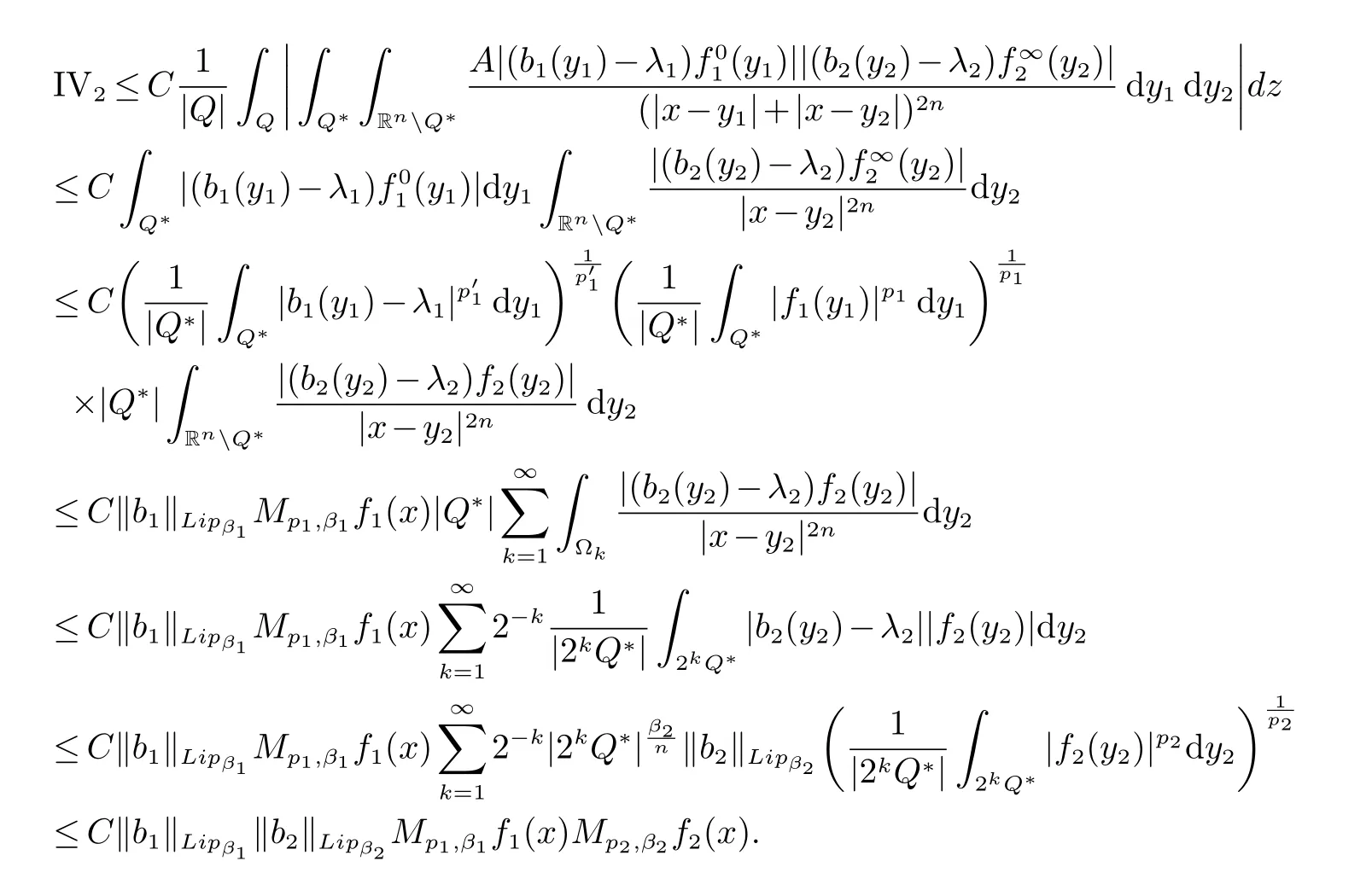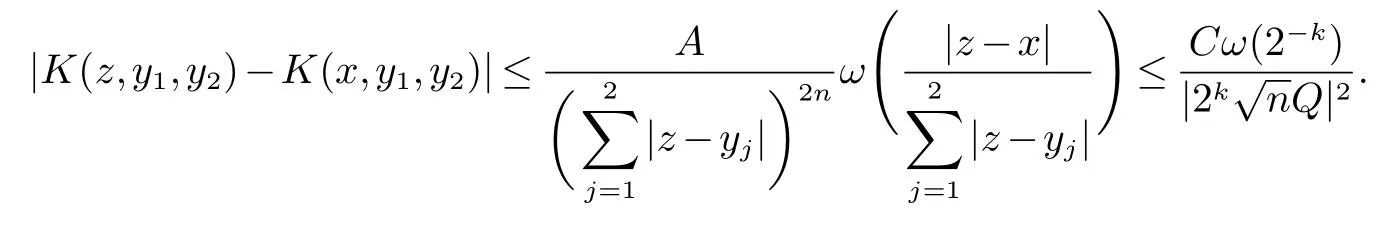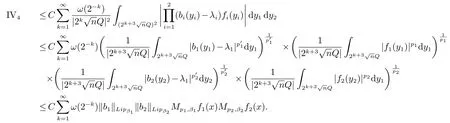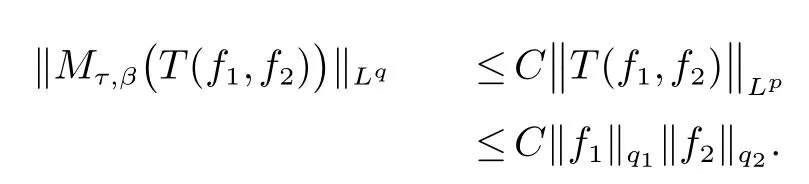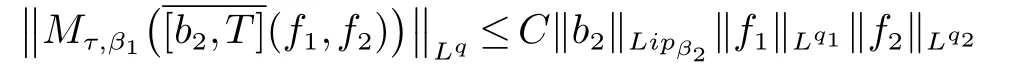带Dini核的多线性Calderón-Zygmund算子的迭代交换子的有界性∗
周疆,胡喜
(新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046)
0 引言
多线性Calderón-Zygmund 理论起源于Coifman 和Meyer 在文献[1]和[2]中的工作.近几十年来,带经典核的多线性Calderón-Zygmund 理论被许多学者进一步研究(见文献[3 −6]).最近,带粗糙核的多线性Calderón-Zygmund 理论逐渐形成(见文献[7 −13]).首先,我们介绍一类带粗糙核的多线性Calderón-Zygmund 算子的定义.
设ω(t):[0,∞)→[0,∞)是一个非减函数且0<ω(1)<∞.对于a>0,如果有
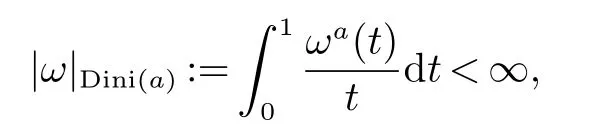
那么称ω ∈Dini(a).显然地,若0 其中X ≈Y 表示存在一个常数C>0,使得C−1Y ≤X ≤CY. 定义1[11]设K(x,y1,...,ym)是定义在(Rn)m+1除去对角线x=y1=···=ym上的局部可积函数,如果K 满足以下三个条件: (i)存在一个常数A>0,使得对任意x 与y1,...,ym不全等的(x,y1,···,ym)∈(Rn)m+1都有 则称K 为Dini 型m-线性Calderón-Zygmund 核. 定义2[11]设T :S(Rn)×···×S(Rn)→S′(Rn),如果满足以下两个条件: (i)存在一个Dini 型m-线性Calderón-Zygmund 核K,使得 (ii)存在1 ≤q1,···,qm<∞ 且使得T 是从Lq1×···×Lqm到Lq上的有界算子,则称T 为带Dini 核的m-线性Calderón-Zygmund 算子,简记T ∈ ω-CZO. 显然地,对某个 ε > 0,当 ω(t) = tε时,ω-CZO 为Grafakos 和Torres 在文献[4]中所研究的经典多线性Calderón-Zygmund 算子. 2009 年,Maldonado 和Naibo 在文献[10]中证明了T 为带Dini 核的双线性Calderón-Zygmund 算子,在 ω 是凹函数且ω ∈Dini(1/2)的条件下,算子T 在乘积Lebesgue 空间上是有界的.2014 年,Lu 和Zhang在文献[11]中将Maldonado 和Naibo 的结果推广到多线性情形,同时削弱了ω 的条件,只需要ω ∈Dini(1).值得注意的是,Lu和Zhang在文献[11]中也做了BMO 线性交换子的结果,但由于交换子相对算子本身有更多的奇性,对于ω 需要如下的更强的条件: 最近,Zhang 和Sun 在文献[13]中考虑了迭代交换子的情形.设且 ω 满足 如果1 定义3[14]设0<β<1,给出Lipβ(Rn)的定义为 2009 年,王伟和徐景实在文献[14]中研究了多线性Calderón-Zygmund 算子与Lipschitz 函数生成的交换子在乘积Lebesgue 空间上的有界性. 受上述工作启发,一个自然的问题是:带Dini 核的多线性Calderón-Zygmund 算子与Lipschitz 函数生成的迭代交换子在乘积Lebesgue 空间上是否有界?注意到,由于Lipschitz 函数的特殊性,本文将文献[13]中BMO交换子的结果做到Lipschitz 交换子时,对ω 满足的条件,可以削弱为ω ∈Dini(1). 定理1设1 便于行文,我们给出一些必要的记号和说明:aB,a>0,表示与球B 同中心,边长伸缩a 倍的球体;C 表示与主要指标无关的常数,每次出现时其值可能并不相同; 对于Rn中的可测子集E,用χE表示E 的特征函数,对1 ≤p ≤∞,p′为p 的共轭指标,即满足 我们首先引入一些相关的定义和结果. 定义4[15]设Sharp 极大函数M♯f 的定义为 其中Q 为Rn中包含x 的方体. 对于0 定义5[14]对非中心极大算子的定义为 引理1[17]若0<β<1,1 ≤p<∞,则有 引理2[17]设0<β<1,f ∈Lipβ,Q1,Q2为Rn中任意两个方体.若Q1⊂Q2,则有 定理证明中,我们将多次使用如下的Kolmogorov 不等式. 设0 为了证明本文的主要定理,需要给出一个关键的Sharp 极大函数估计,即引理3.这一方法可以在文献[6]中找到.不失一般性,我们只证明m=2 的情形,即考虑 引理3设0<β1,β2<1,b1∈Lipβ1,b2∈Lipβ2,T ∈ ω-CZO,且 ω ∈Dini(1).如果且p1,p2>1,那么存在一个常数C>0,使得对有 其中 证明固定x ∈Rn,Q 为Rn中包含x 的方体.对于a,b ∈R,0 因此,为了证明(1)式,只需证明 对 ∀λ1,λ2∈R,z ∈Rn,有 进而可得 从而有 其中 II,III 和IV 类似. 下述证明过程中,取λi=(bi)Q,i=1,2. 首先估计I,由Hölder 不等式及引理2,可得 下面估计II,由Hölder 不等式及引理2,可得 类似于II 的估计,可得 最后,估计IV. 其中 进一步地有 首先估计IV1,由Kolmogorov 不等式,算子T 的有界性,引理2及对指标p1,p2>1 分别运用Hölder 不等式,可得 对于x,z ∈Q,y ∈RnQ∗,易知|x−y|≈|z −y|. 接下来估计IV2,由核K 满足的条件,引理2,引理3 及对指标p1,p2>1 分别运用Hölder 不等式,可得 对于IV3这一部分,类似于IV2的估计,可得 最后估计IV4,取对于0<δ<1,由Hölder 不等式知 注意到,对任意x,z ∈Q 和任意y1,y2∈Ωk,有 则由ω 是非减函数,且由核K 满足的条件,可得 进而由引理3,ω ∈Dini(1)及对指标p1,p2>1 分别运用Hölder 不等式,可得 综合以上估计,即证明了(1)式.类似地,可以证明(2)和(3)式,这样便完成了引理3 的证明. 定理1 的证明:对中稠密,因此只需证明对成立即可. 根据引理3 及Fefferman-Stein 不等式,可得 对于1 < q1,q2< ∞,可以选择引理3 中的p1,p2,使得1 < p1< q1,且1 < p2< q2.令由则有 从而有 类似地,我们有 和 从而有 这样便完成了定理1的证明. 注:在运用Fefferman-Stein 不等式时,需要在不等式左边小于无穷的条件下,这一部分内容可以参看文献[6].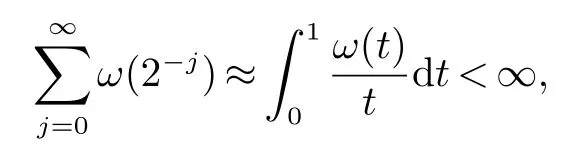




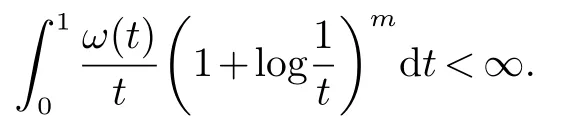
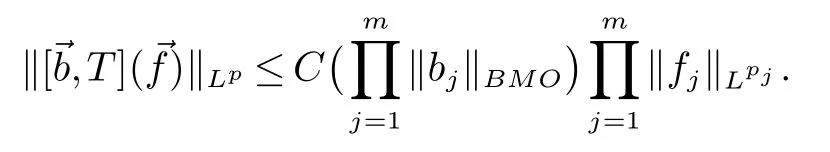


1 预备知识

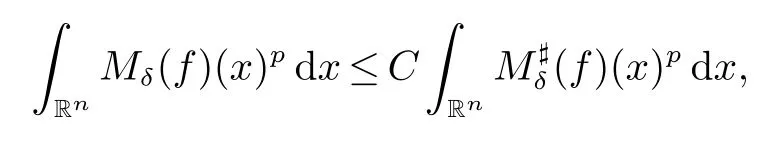


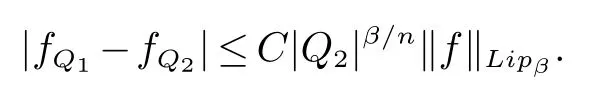
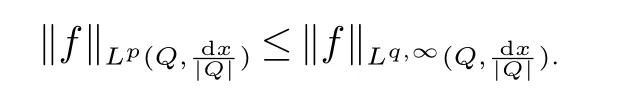
2 主要结果及其证明