基于混合阈值的清除重复间隔阈值经验模态分解去噪方法

王平根，吕敬祥,2

基于混合阈值的清除重复间隔阈值经验模态分解去噪方法

王平根1，*吕敬祥1,2

(1. 井冈山大学电子与信息工程学院，江西，吉安 343009；2. 江西省农作物生长物联网技术工程实验室，江西，吉安 343009)

经验模态分解(Empirical mode decomposition,EMD)被认为是一种有潜力的非线性非静态信号去噪方法。传统的经验模态分解阈值去噪在零点附近存在不连续性的缺点，Kopsinis提出了EMD-IIT和EMD-CIIT方法，但这两种方法对阈值过于敏感，即区间极值轻微的偏差就有可能导致去掉整个区间曲线，因此本文提出一种混合阈值算法，结合了EMD-DT和EMD-IT各自的优势。仿真结果表明此去噪算法具有较好的效果。

经验模态分解；间隔阈值经验模态分解；混合阈值；去噪

0 引言

从观测到的含噪数据中恢复出原始有用信号是信号处理中的一个经典问题，研究者已从各个角度提出了一些去噪方法1-2]。最早的线性方法由于设计和实现简单已得到了广泛的应用，然而这些方法对含尖锐的边沿信号、短时脉冲信号的去噪效果较差。事实上，自然界真实的信号通常是非线性非平稳的，为了克服这些困难，学者们提出了一些非线性处理方法。在这些非线性方法中，小波阈值去噪已得到了较广泛的应用[3]，但这种方法的主要缺陷是必须事先选定小波基函数，选择何种基函数至今仍没有明确的理论指导，靠设计者的经验。与小波方法相比，经验模态分解（Empirical Mode Decomposition, EMD）不仅能够实现小波方法的多分辨率分析，而且能克服小波变换方法中必须提前选择小波基函数的困扰。

基于EMD的信号去噪方法可分为两类[4-5]：1）直接抽取法，进行EMD分解后选择其中的若干个IMFS进行重构；2）阈值处理法，进行EMD分解后，选择一个合适的阈值与IMFS幅度进行比较，然后再进行重构。目前，在阈值的选取方面，流行的方法主要有两种[6-7]，一种是直接阈值法[8]（EMD-DT），这类方法容易忽略IMF分量的间歇过零点；另一种是间隔阈值法[9]（EMD-IT），该方法的原理是将IMF分量相邻两个过0点间的曲线看做一个整体，有效保留信号特征的同时还能减少模态混叠。许多学者对基于（EMD-IT）的阈值去噪进行了进一步改进，如：区间极值迭代阈值方法（EMD-IIT）、清除重复间隔阈值（EMD-CIIT）去噪方法[10]。本文在深入研究现有的关于EMD-DT和EMD-IT去噪方法基础上，进一步挖掘噪声对IMF影响的主要因素，提出一种混合EMD-CIIT去噪方法。

1 EMD简要回顾

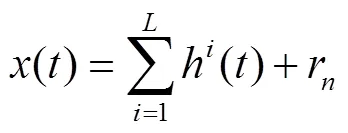
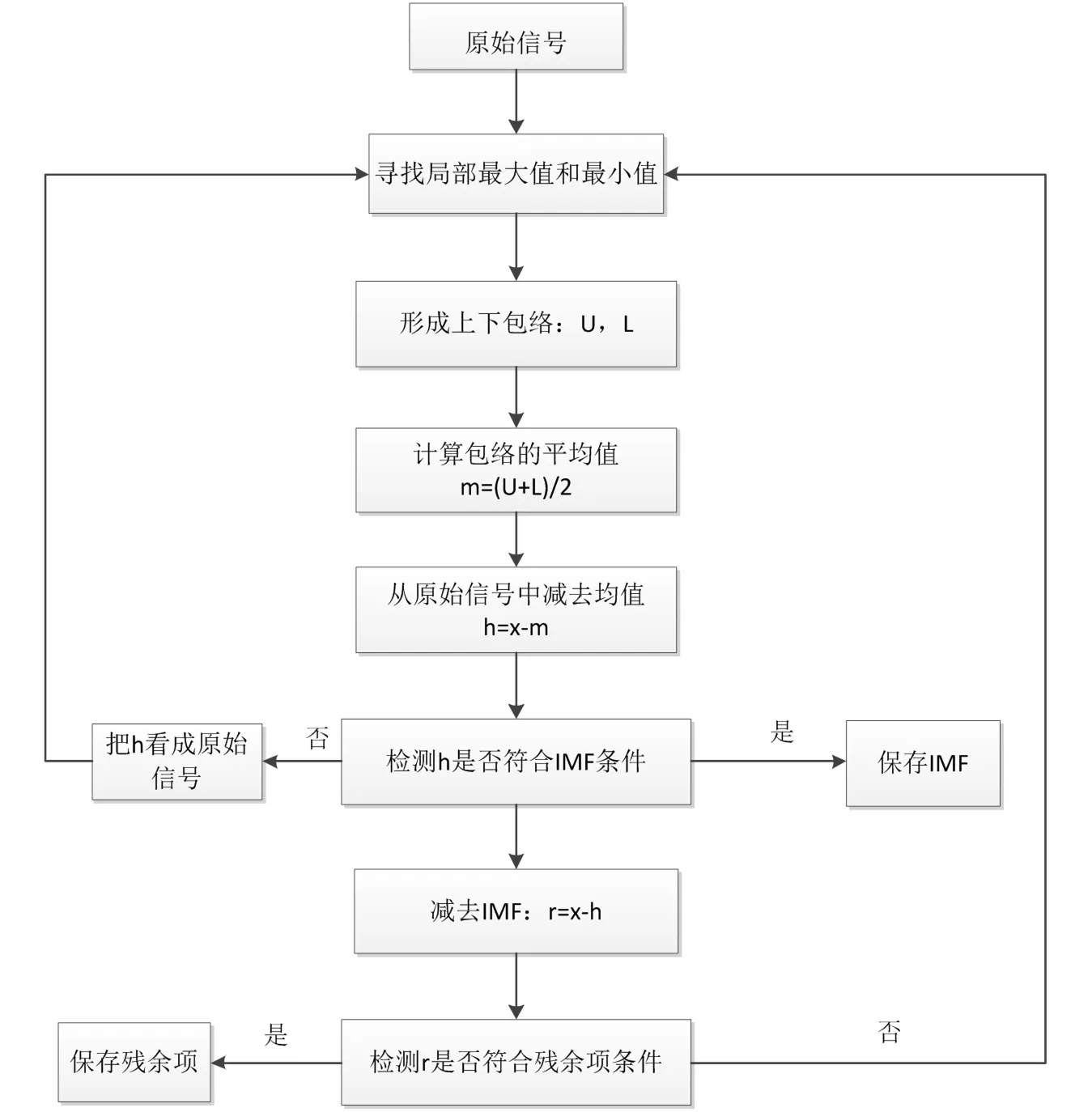
图1 EMD流程图

2 EMD阈值去噪方法

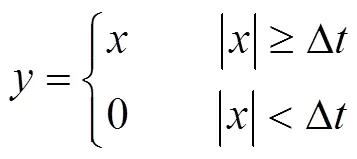
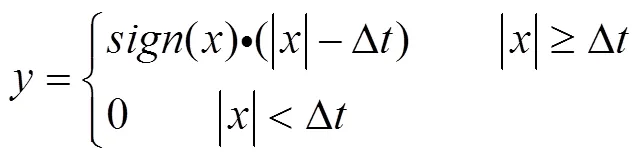
除了标准的阈值去噪方法，学者们也进行了一些修改，如基于贝叶斯小波阈值方法[11]和平移不变小波阈值方法[12]。

2.1 直接阈值去噪

仿效小波的阈值去噪方法，经验模态分解阈值去噪方法（EMD-DT）也可分为硬阈值和软阈值方法，可用式（3），式（4）表示:

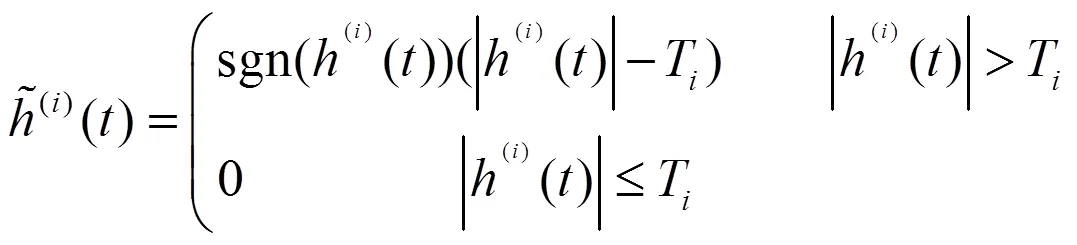
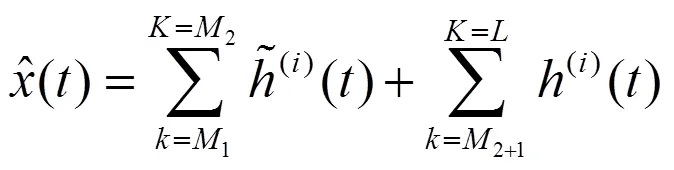
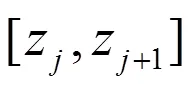
2.2 间隔阈值去噪

间隔EMD阈值是以相邻过0点间的信息段为单位的数据处理方法，同样分为硬阈值方法和软阈值方法，分别可用式（7）、式（8）表示。

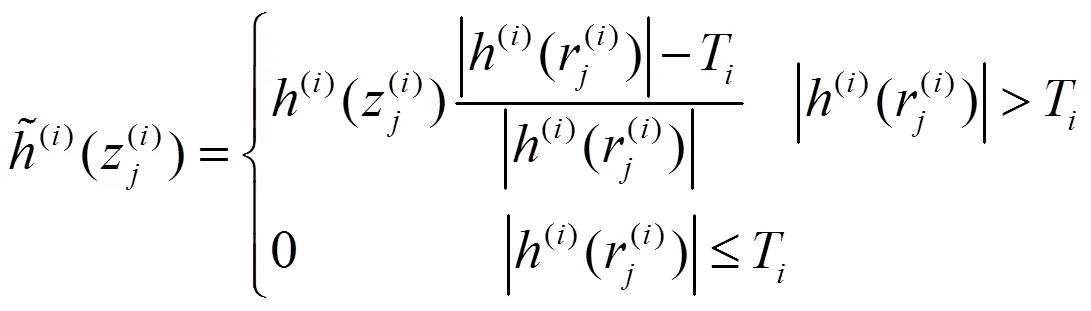
2.3 迭代间隔阈值去噪方法

在小波阈值去噪中，为了克服信号不连续产生的Pesudo2Gibbs现象，对含噪信号进行循环平移后再去噪，这种方法叫平移不变小波变换，运用这种思想到EMD中，研究者提出一种迭代间隔阈值去噪方法EMD-IIT[14-15]。该方法的主要步骤如下。

1）利用EMD分解原始含噪信号，得到相应的固有模态分量；

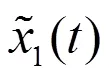
显然，该方法仍存在不可避免的缺点，当信号的信噪比较高时，在第一阶的IMF中就有可能包含了部分有用的信号，这种情况下随机的去改变采样点位置，固有模态分量中所包含的有用信号蔓延从而影响信号的去噪性能。针对这种情况，学者们也研究了一些改进措施，如清除重复间隔阈值（EMD-CIIT）方法。

3 混合阈值的EMD-CIIT消噪方法描述

EMD-IIT和EMD-CIIT这两种方法从本质上看仍没有脱离软阈值去噪方法的核心原理，与EMD-DT相比，这些算法对阈值更敏感。为了更加清楚地说明这个问题，本文用图2进行演示，区间极值稍微有点偏差时，所有的这些基于软阈值去噪方法把整个区间曲线都去掉，此时，有可能比基于硬阈值去噪方法的性能更差。因此，本文考虑到不同算法的优点，采用混合阈值的去噪算法。这种方法在充分利用区间极值的基础上再引入区间中位数，如果中位数大于阈值，此时采用EMD-IT方法去噪；如果区间中位数小于阈值，但是区间极值大于阈值，此时采用EMD-DT进行去噪；当区间极值小于阈值时，则去掉整个区间数据，这个过程可以用式（9）表示。

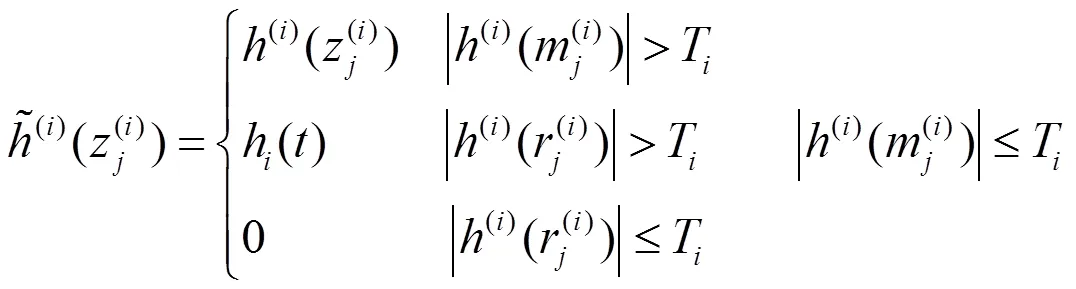
4 仿真结果及分析

采用如图3所示的Blocks、Doppler、Bumps三种具有典型特征的仿真信号来验证算法去噪性能。另外，引入信噪比和均方误差来评估去噪效果：信噪比越大，均方误差越小，表明去噪效果越好，计算公式分别如式（10）、式（11）。为了对比去噪效果，对噪声信号分别采用EMD-DT、EMD-IT、EMD-CIIT和本文所提的混合阈值EMD-CIIT法进行去噪。

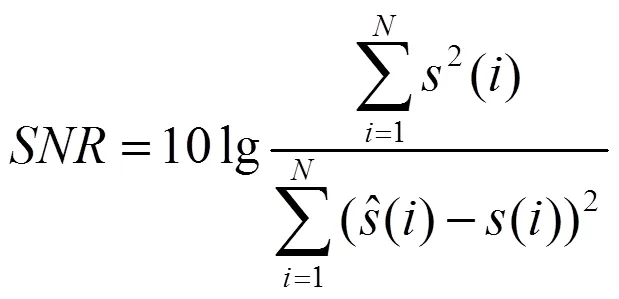
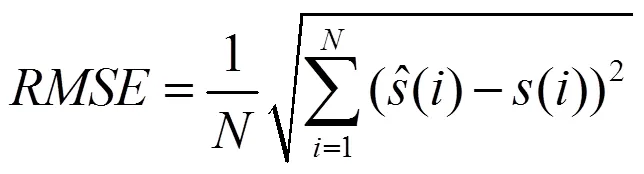
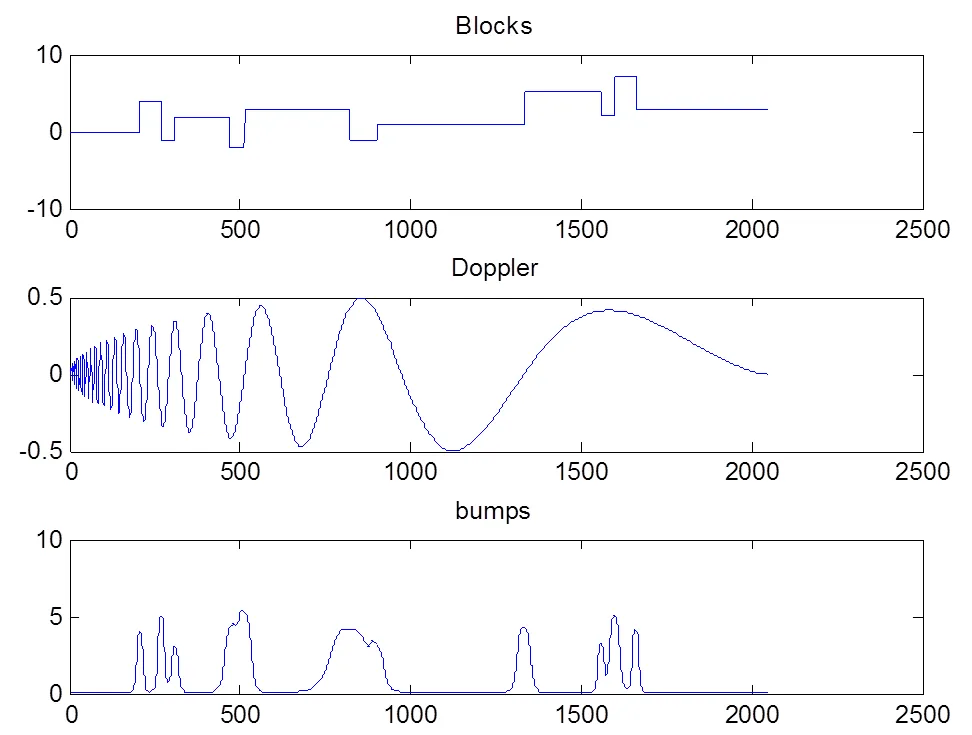
图3 Blocks, Doppler, Bumps三种不同信号示意图

利用wnoise生成不同信噪比的含高斯白噪声的测试信号，其信噪比SNR分别为0dB、5dB、10dB、15dB、20dB，信号长度取为2048。图4显示不同信噪比去噪前后算法性能，可以清楚地看出所提新算法与其他两种算法相比，对三种不同的测试信号都有更好的去噪性能。这种性能改善的主要原因在于所提新算法根据IMF的特征不仅考虑了连续性问题也考虑了非连续性问题，即混合地运用了直接阈值和间隔阈值。

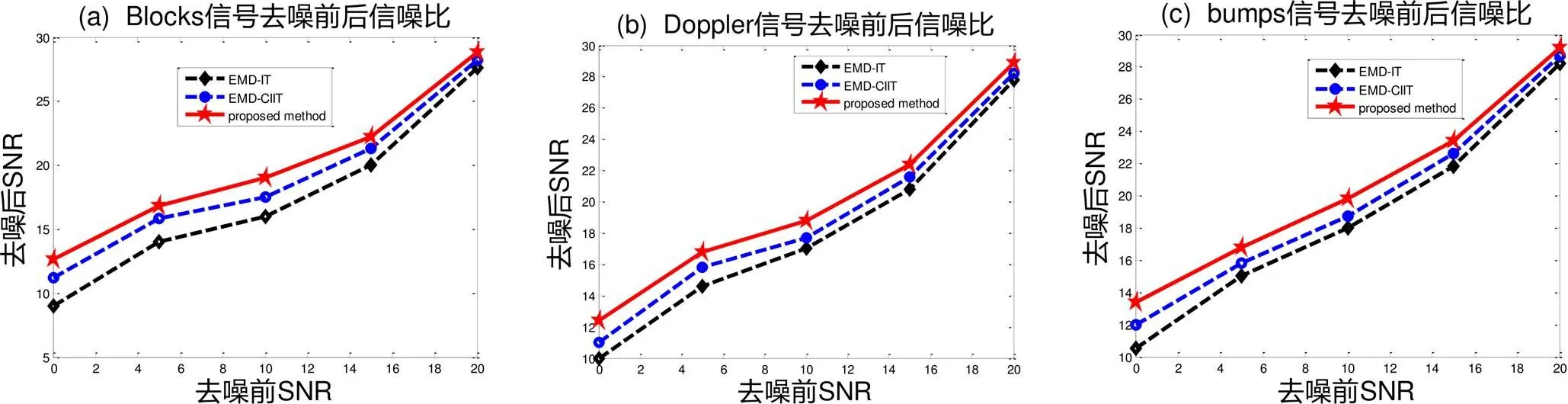
图4 三种不同信号采用不同方法去噪效果

图5是SNR=10时，信号长度为2048，利用文中所提方法对测试样本Bumps信号的去噪效果图。表1呈现了对不同信噪比的Bumps仿真信号经三种方法去噪后MSE。

表1 Bumps信号三种方法去噪后的均方误差

Table 1 Mean Square error of Bumps signal after denoising by three methods

方法均方值 0dB5dB10dB15dB20dB EMD-IT0.03250.01310.0070.00620.0057 EMD-CITT0.0290.01120.00670.00540.0049 被提方法0.02030.01050.00550.0050.0043

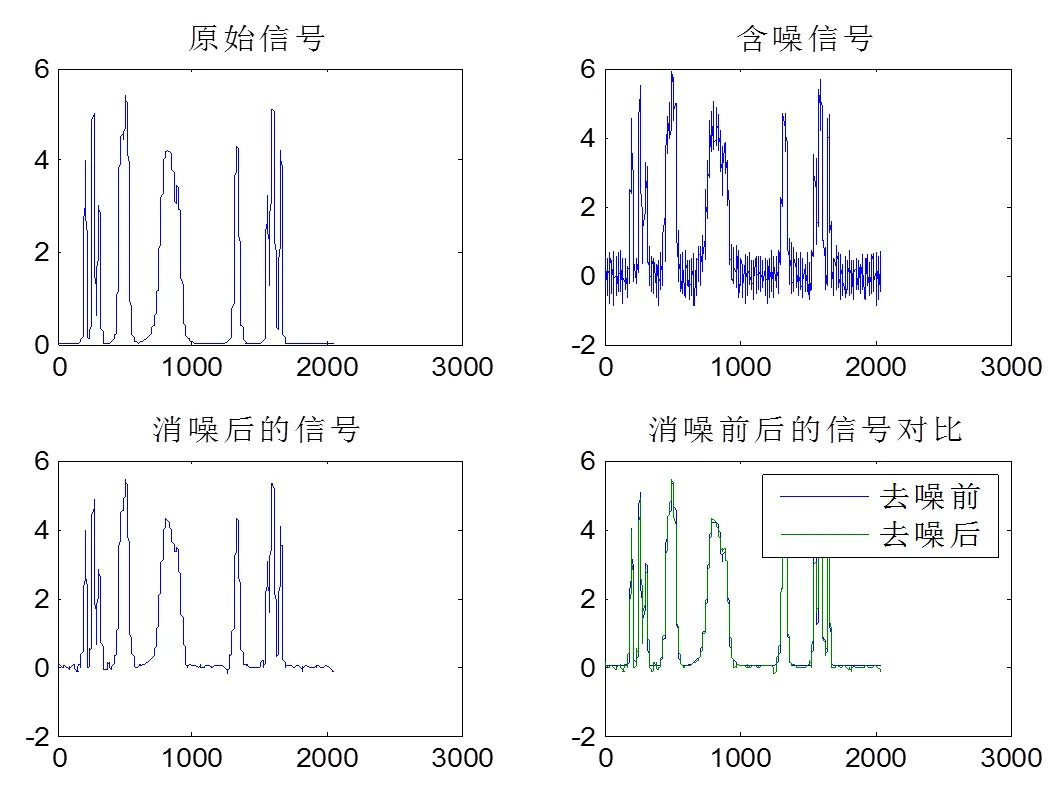
图5 SNR=10dB bumps信号原始数据与去噪数据对比

5 结论

针对间隔（区间）阈值去噪算法对阈值过分敏感的问题，本文提出了一种混合阈值EMD-CITT去噪方法。该方法通过引入中位数实现了阈值与区间极值及中位数分别比较，从而巧妙地实现了点结构硬阈值去噪方法同时又能实现间隔结构的软阈值去噪方法。通过运用Blocks、Doppler、Bumps三种具有典型特征的仿真信号来验证算法去噪性能，仿真实验结果表明，与现有的EMD去噪方法相比，本文方法在信噪比、噪声均方差方面都有一定的改善。

[1] Li B , Zhang L , Zhang Q , et al. An EEMD-Based Denoising Method for Seismic Signal of High Arch Dam Combining Wavelet with Singular Spectrum Analysis[J]. Shock and Vibration, 2019, 2019:1-9.

[2] 杨帅,胡学钢,张玉红. 用于域适应的多边缘降噪自动编码器[J]. 计算机科学与探索, 2019, 13(02):146-153.

[3] Yang G, Liu Y, Wang Y, et al. EMD interval thresholding denoising based on similarity measure to select relevant modes[J]. Signal Processing, 2015, 109(C):95-109.

[4] Shi P, An S, Li P, et al. Signal feature extraction based on cascaded multi-stable stochastic resonance denoising and EMD method[J]. Measurement, 2016, 90:318-328.

[5] Mohguen W, Bekka R E. Improvement of the EMD-SG denoising method[C]. International Conference on Electrical and Electronics Engineering. 2016.

[6] 李猛,蒋立辉,熊兴隆,等. 激光雷达信号的可变间隔阈值经验模式分解去噪法[J]. 强激光与粒子束, 2014, 26(11):8-12.

[7] Meng L, Jiang L H, Xiong X L. A novel EMD selecting thresholding method based on multiple iteration for denoising LIDAR signal[J]. Optical Review, 2015, 22(3):477-482.

[8] Wang M, Zhou Z, Li Z, et al. An Adaptive Denoising Algorithm for Chaotic Signals Based on Improved Empirical Mode Decomposition[J]. Circuits, Systems, and Signal Processing, 2019, 38(6):2471-2488.

[9] Yang G, Liu Y, Wang Y, et al. EMD interval thresholding denoising based on similarity measure to select relevant modes[J]. Signal Processing, 2015, 109:95-109.

[10] Kopsinis Y, Mclaughlin S. Development of EMD-Based Denoising Methods Inspired by Wavelet Thresholding[J]. Signal Processing IEEE Transactions on, 2009, 57(4):1351-1362.

[11] Wang X, Li X, Lai W. Remote sensing image denoising based on watershed and Bayesian estimation threshold wavelet algorithm[J]. Energy Procedia, 2011, 11:5043-5049.

[12] Wang Z Z, Ren Z, Liu G D. Study on an improved wavelet shift-invariant threshold denoising for pulsed laser induced glucose photoacoustic signals[C]. Applied Optics and Photonics China, 2015:9674(07-18).

[13] Flandrin P, Goncalves P, Rilling G. Detrending and denoising with empirical mode decompositions[C]. Signal Processing Conference, 2004, European. IEEE, 2004:1581-1584.

[14] Herold C, Wenig S, Leibfried T. Advanced de-noising of power cable Partial Discharge signals by Empirical Mode Decomposition[C].Universities Power Engineering Conference (AUPEC), 2010 20th Australasian. IEEE, 2010: 1-5.

[15] 钟金良,景新幸,杨海燕,等. 一种改进阈值函数的EMD-CIIT语音去噪算法[J]. 桂林电子科技大学学报, 2016, 36(1):9-13.

Denoising methods based hybrid thresholding empirical mode decomposition clear iterative interval thresholding

WANG Ping-gen1,*LV Jing-xiang1,2

(1. Faculty of Electronics and Information Engineering, Jinggangshan University, Ji’an, Jiangxi 343009, China ; 2. Jiangxi Engineering Laboratory of IoT Technologies for Crop Growth, Ji’an Jiangxi 343009, China)

Empirical mode decomposition is considered as a potential nonlinear and non-static signal denoising method. The traditional empirical mode decomposition threshold denoising has the disadvantage of discontinuity near zero. Kopsinis proposed the iterative EMD interval-thresholding and clear iterative EMD interval-thresholding methods. However, the two methods are too sensitive to the threshold. That is, the slight deviation of the interval extreme value may lead to the removal of the entire interval curve. Therefore, a hybrid thresholding algorithm which combines the strengths of EMD-DT and EMD-IT methods is proposed in this paper. Simulation results show that the denoising algorithm has good results.

Empirical Mode Decomposition; EMD interval thresholding; hybrid thresholding; de-noising

TN911.7

A

10.3969/j.issn.1674-8085.2019.06.008

1674-8085(2019)06-0041-06

2019-07-14；

2019-08-30

国家自然科学基金项目（51867011）；江西省教育厅科技计划项目（GJJ180576）

王平根(1964-)，男，江西吉水人，高级实验师，主要从事计算机网络和数据库等研究(E-mail: wangPingGen@163.com);

*吕敬祥(1977-)，男，湖南邵阳人，讲师，博士，主要从事信号与信息处理，WSN等研究(E-mail: Ljingxiang2013@163.com).