柔性臂振动的双目三维检测和主动控制

邱志成 肖骏 刘金国

摘要：针对柔性臂的振动问题，设计并搭建了一套基于双目视觉检测，以伺服电机驱动控制的柔性臂实验平台进行研究。根据电机的运行状态将柔性臂振动分为定点振动和旋转振动，通过双目视觉对柔性臂上的特征点进行三维重建，进而获取柔性臂的定点和旋转振动信号。对振动信号进行模态分析获取柔性臂的振动特性，并据此设计基于蚁群优化参数的PD控制器抑制柔性臂的弯曲振动，然后与常规PD控制效果进行比较。实验结果表明，基于蚁群优化参数的PD控制能够在较短时间內有效抑制柔性臂的定点振动，相较于常规PD控制抑振效果有明显改善，并且旋转振动的抑制效果也很显著，以此验证了蚁群PD控制算法在快速抑振上的有效性。

关键词：柔性臂;双目视觉;三维重建;蚁群优化;振动控制

DOI：10.15938/j.emc.2019.10.015

中图分类号：TP241文献标志码：A 文章编号：1007-449X（2019）10-0129-10

0引言

柔性材料由于质量轻、灵活度高等特点，在航空航天领域中被广泛应用于柔性关节和太阳能帆板等结构上，其中不乏细长的柔性臂结构。此类结构易受激产生持续振动从而影响航天器的正常工作。因此对柔性臂结构的振动控制研究具有重要意义。

目前对于柔性臂结构的振动问题国内外已有大量相关研究和文献，包含了各种动力学建模思想和振动检测控制方法等。Chu和Cui采用压电驱动器和应变仪，基于输入整形器和自适应正位置反馈，研究了双连杆柔性臂的振动控制问题。Qiu等使用压电片检测旋转双连接柔性梁的振动信号，使用有限元法对系统进行动力学建模分析，并设计了智能主动控制算法进行振动抑制。朱晓锦等利用光纤光栅材料研究了太空柔性多关节机械臂，仿真实现了柔性结构的振动形态三维拟合和可视化显示。

以上方法多采用压电陶瓷片或者加速度计作为柔性臂振动检测的传感器，这些接触式测量手段带来的附加质量会在一定程度上改变柔性臂的结构特性，影响实验效果。而双目视觉作为一种非接触式的测量手段可以有效避免前者的缺陷，同时获取视场范围内的多特征点的三维信息。杨唐文等研究了一种基于双目视觉的运动物体实时跟踪与测距的实现方法，提出了一种无需重新标定即能实现运动目标搜索和测量的算法。张春芳针对大型柔性在轨结构，探索了基于双目视觉进行振动测量的方法，但是并没有探讨振动抑制的问题。

蚁群算法是一种最新发展的仿生优化算法，最初在解决著名的旅行商问题（travelling salesmanproblem，TSP）上得到有效应用。蚁群算法是通过内部信息的积累和多次迭代更新而收敛于最优路径，因此具有全局的收敛能力，但是由于寻优开始阶段信息素不足，从而导致了寻优初期内部信息累积时间相对较长，求解相对缓慢。该算法采用正反馈并行自催化机制，具有较强鲁棒性、优良的分布计算机制、易于与其他算法结合等优点。K.V.Laksh-mi Narayana等针对锥形顶储罐开发了基于蚁群参数优化的PID参数自调节控制器，改进了设定值的跟踪效果。然而目前还没有将蚁群优化算法用于优化控制器参数，以控制柔性臂结构振动的相关研究。

针对现有研究中的不足，本文基于双目相机和伺服电机搭建了一套用于柔性臂振动测控的实验平台，驱动电机的起停使柔性臂产生定点振动和旋转振动;然后采用双目三维重建的方法对柔性臂的定点和旋转振动信号进行检测和分析，获取臂结构的振动特性，并据此设计了基于蚁群优化参数的PD控制器，通过实验观察控制效果并与常规PD控制进行比较。实验结果验证了提出控制算法的有效性。

1实验控制系统构成

图1显示了实验系统控制结构示意图。柔性臂一端通过轮毂固定在行星减速器输出轴上，另一端表面粘贴有黑色圆片承载振动信息，整体通过伺服电机经由减速器减速后驱动;2个工业相机固定在滑轨上，采集图片经由网线传输至计算机进行相应处理;电机驱动信号由计算机生成，经由运动控制卡传递到伺服驱动器上，以速度模式驱动电机旋转。

本实验中的数据是以一定的采样频率采集的，故需将状态空间方程按对应的采样周期T_s进行离散化处理;离散化状态空间方程模型可根据采集好的输入输出数据，用MATLAB辨识工具箱进行辨识。

2双目三维重建

双目立体视觉模拟人眼对空间的感知，利用两台摄像机同时获取同一场景的图像对，进而进行场景重建、目标定位和测距等。图2所示为双目视觉的三维重建过程的几个主要步骤。

由于双目三维重建的特征点提取不受柔性臂姿态的影响，因此非常适用于相机视场范围内柔性臂大范围运动时的定点和旋转振动检测。

2.1针孔摄像机模型及其标定

根据摄像机标定原理，像素坐标系O_o-UV中的像素点（u，v）和世界坐标系O_w-X_wY_wZ_w中的三维点（x_w，y_w，Z_w）之间存在转换关系为

其中z_c表示目标点在相机坐标系O_c-X_cY_cZ_c中Z_c轴的坐标，f_x和f_y分别是图像坐标系O₁-XY中X轴和Y轴方向的归一化焦距，（u_o，v_o）是光心在像素坐标系O_o-UV下的坐標;R=（r_ij）_3×3和T=（t_x，t_y，t_z）^T分别为旋转矩阵和平移矩阵，用来描述O_c-X_cY_cZ_c和O_w-X_wY_wZ_w之间的转换关系。式中，f_y，f_y，u_o，v_o4个参数只与相机内部结构有关，称为相机内部参数;而矩阵R和向量T与相机的位置及姿态有关，而与相机结构无关，称为相机外部参数;确定相机内、外部参数的过程，就是相机标定。本文采用基于棋盘格标定板的张正友标定法，通过MATLAB标定工具箱对相机进行标定。

2.2双目空间坐标测量模型

图3为两台相机组成的双目测量模型示意圖。其中，O_w-X_wY_wZ_w下空间中任意一点P（x，y，Z）在两相机拍摄下的像素坐标为p₁（u₁，v₁）和p₂（u₂，U₂）。

上标表示相机编号，采用最小二乘法求解得到

P=（A_TA）^-1A_TB。

（6）

这样在已知两相机内外参以及特征点投影的一对像素坐标的情况下，便可由式（6）重建出空间任意一点的三维坐标。

2.3柔性臂振动检测方案

2.3.1特征点三维坐标测量

柔性臂表面粘附的两块黑色圆片跟随柔性臂一起振动，作为承载振动信息的特征图样，其圆心便是需要进行三维重建的特征点。

对于实时采集的图像，首先需要校正因镜头产生的图像畸变，降低图像像素误差。然后进行图像预处理，包括图像感兴趣区域（region of interest，ROI）提取、图像滤波和阈值分割等，目的是降低图像噪声，突出特征图样，提高图像处理的速度和准确性。接着进行边缘检测和提取，以便分离和提取出黑色圆片的轮廓，并对其轮廓以椭圆拟合，从而得到圆心的像素坐标。图4显示了ROI提取和椭圆拟合的效果。

最后对左右相机采图得到的特征点进行立体匹配，利用得到的像素坐标对根据式（6）求出特征点的三维坐标，完成三维重建。

2.3.2振动信号获取

1）柔性臂定点振动检测。

柔性臂的定点振动是指当伺服电机在静止状态下由外力激振而产生的振动。首先任取一圆片的圆心P为特征点，作为柔性臂振动信息的反馈。对于定点振动，首先需要明确臂的初始状态，故在激振前先拍摄60帧臂的静止状态的图像，依次处理得到特征点的三维坐标后，取平均值作为初始点的初始世界坐标P_o（x_o，y_o，z_o），即：

激振之后，对采集到的t时刻的图像进行处理得到圆心P的世界坐标P（t）=（x（t），y（t），Z（t）），对于小幅值振动，振动位移S（t）可用点P和P_o之间的欧式距离来衡量，由于世界坐标系的Z轴基本与柔性臂表面垂直，故正负基于z（t）-Z_o的符号来判定，即

2）柔性臂旋转振动检测。

柔性臂的旋转振动是指当伺服电机带动中心刚体旋转时被自身力矩激励而产生持续振动。图5为柔性臂旋转振动示意图。

为了求解P′点的坐标，需要确定中心转轴在世界坐标系O_w-X_wY_wZ_w下的表达，假设转轴通过一点Q=（x_q，y_q，Z_q）且方向为n=（n_x，n_y，n_z），则该转轴被完全定义。利用相机采集柔性臂以初始位置为基准，转角在±45°范围内（视场范围内）均布的一系列图像，然后通过图像处理得到包含P点位于不同位置时的空间点集S={P_i（x_iy_iz_i|i=1，2，…}（在空间中实际上呈一段圆弧状）。对点集S按公式Ax+By+Cz+D=0进行平面拟合，显然转轴应垂直于拟合平面π，故可令

n=（n_x，n_y，n_z）=（A，B，C）。（10）

然后按公式（x_c-x）²+（y_c-y）²+（Z_c-z）²=r²进行圆锥拟合，其中r为一定值且应比点P的旋转半径大。拟合得到的点C（x_c，y_c，z_c）和S包含点的连线实际上构成了某一圆锥的一系列母线，显然点C作为锥顶应在转轴上，故可令

Q=（x_q，y_q，Z_q）=（x_c，y_c，Z_c）。（11）

拟合过程可用MATLAB的cftool工具箱完成。

将式（13）代入式（9）中，可求出臂的旋转振动位移。

3基于蚁群优化的PD控制器设计

蚁群算法是一种针对离散优化问题的元启发式算法，它利用一群人工蚂蚁的协作进行寻优。针对PD控制参数的蚁群优化，首先需要定义一个有向图，并且使得图中的完整路径所包含的节点和PD参数具有——映射关系;然后单个蚂蚁对爬过的路径所对应的PD参数根据事先定义好的适度函数评价其优劣，接着在路径上留下相应的信息素，作为蚂蚁之间互相协作的媒介;随着蚂蚁路径寻优过程的迭代，那些优良的解所包含的路径将会有更多的信息素沉积，从而有更大机会吸引蚂蚁通过，进而加强路径的吸引力;最后在迭代末期，整个蚁群将逐渐向包含最优路径的参数收敛，达到自动优化PD参数的目的。图6所示为基于蚁群优化的PD控制器的算法框图。

3.1PD参数的蚁群优化问题抽象

图7所示为将PD参数抽象而成的包含一系列节点的有向图。

图中共有7列节点，每列的编号如图上方的数字所示，其中位于第0列的s节点为起始结点，其余6列各自包含从0到9共10个节点。人工蚂蚁从S节点开始，从左往右依次选择各列的一个节点爬行，直到第6列某一节点后停止，完成一次完整路径的构建。由此可见，一条完整的路径即为一个6位数的数字序列，假设该6位数前三位组成的十进制数N_p代表参数K_p，后三位组成的十进制数N_d代表参数K_d，两者的转换关系为：

其中的[K_pmin，K_pmax]和[K_dmin，K_dmax]分别用于限制K_p和K_d的取值范围。至此PD参数的优化过程便转化为了人工蚂蚁在有向图上寻找最优路径的过程。

3.2适度函数建立

适度函数用于评价PD参数的优劣，其选择合理性关乎系统的控制性能，为了获得较好的控制效果，可以将系统的输出量和控制误差作为考量指标。因此，采用适度函数为

J=w₁|e（k）|+w₂u²（k）。（15）其中k表示当前迭代次数，w₁和w₂为权值，视具体实验情况而定。

3.3节点选择

蚂蚁爬行节点的选择是路径构建的基础。约定第m列第i节点的编号为（m，i），且起始结点S的编号为（0，0），记τ_m（k）_ij表示节点（m，i）和节点（m+1，j）之间路径的信息素浓度，η（k）_mj表示节点（m，j）对第m-1列所有节点的可见度，则蚂蚁从节点（m，i）进入节点（m+1，j）的概率P_m=（k）_ij规定如下

其中：M_m+1表示第m+1列节点的集合;α和β分别表示信息素浓度和可见度的影响因子。

而蚂蚁选择下一节点S的规则为：

其中：M_m+1表示第m+1列节点的集合;α和β分别表示信息素浓度和可见度的影响因子。

而蚂蚁选择下一节点S的规则为：

其中k（为全局信息素更新系数。

当所有蚂蚁都完成了各自的路径后，首先对最优和最劣路径上的信息素单独更新：

然后对有向图中所有路径的信息度和节点的可见度进行更新，全局更新规则如下：

其中：λ为信息素蒸发常数;N_mi（j）表示第j轮迭代中节点（m，i）被所有蚂蚁经过的次数。

3.5算法流程

1）初始化蚁群优化系统参数，开始迭代循环;

2）置m只蚂蚁于S结点，依式（17）让每只蚂蚁先后依次自行寻径至终点;

3）所得路径依式（14）算出对应PD参数，计算目标函数值，并依式（18）更新局部信息素浓度;

4）寻径全部完成后更新当前全局最优解，并依式（19）和式（20）更新全局信息素浓度和节点可见度;

5）将本轮迭代全局最优解输出给PD控制器;

6）进入下轮迭代，重复2）-5），直至控制停止。

4柔性臂振动控制实验

4.1实验装置

系统实验装置如图8所示，该实验平台由柔性臂、2个工业相机（位于左下角的小图中）、三菱伺服组件、行星减速器、运动控制卡和计算机组成。伺服电机额定功率100w，以速度控制模式工作;减速器减速比为1：25;柔性臂为环氧树脂材料制成，弹性模量E=34.64GPa，密度ρ=1840kg/m²，长度l=750mm，宽度b=97mm，厚度d=2mm;运动控制卡采用固高运动控制器，型号为GTS-400-PV-PCI;双目相机使用映美精型号为DFK 21BU04的CCD工业相机，分辨率640×480，最高拍攝帧率60Hz。

本实验中，柔性臂振动检测和抑制过程如下：首先利用双目相机采集柔性臂的实时振动图像，获得含有振动信息的图像序列并经由Gige网线传输至其中g为（0，1）之间的一个随机数，g_o为贪心规则的概率值。

3.4信息素和可见度更新

在一轮迭代中，当一只蚂蚁爬完一条完整路径后，需要对所经过路径上的信息素浓度进行局部更新，局部更新的规则为计算机中;然后基于标定的双目视觉模型和OpenCV计算机视觉库，通过相应的图像处理算法对采集的图像进行处理以获取柔性臂的振动位移信息;接着以此作为振动主动控制算法的输入量，运行算法得到实时的抑振信号，经由运动控制卡的D/A模块输出到电机伺服驱动器中，驱动伺服电机的运转从而抑制柔性臂的振动。整个实验装置便是通过这样的负反馈闭环控制环节对柔性臂振动进行抑制，其控制算法使用C++编程语言在VS2010环境下编写MFC界面控制程序实现。

本实验使用的柔性臂二阶固有频率约为15Hz，对于二阶以上的高阶频率，由于频率高且振动位移小，对于60Hz频率的相机而言检测精度难以达到要求，故本文暂且只对一阶频率的检测和控制进行探讨，而高频振动的检测有赖于相机硬件配置的提升和相关技术的发展。本实验中的计算机对相机实时采集的单张图片的处理耗时约为4ms，相对于相机16.6ms的采样间隔而言，具有充足的时间对双目相机采集的两幅图像进行处理，进而可以保证实时性的要求。

4.2定点振动控制实验结果和比较

首先通过实验采集柔性臂的自由振动信号，采样频率为60Hz，激励方式为用激振小锤敲打。

图9为柔性臂定点自由振动的位移曲线。由图可知，柔性臂的初始最大振幅约为40mm，经过2.5s衰减为50%，经过4.5s衰减为20%，且依然有较持久的残余振动;另外柔性臂的一阶振动频率约为2.0Hz，根据采样定律，相机60Hz的采样频率完全满足要求。综上，自由振动在不受控制的情况下将持较长时间。以下实验为了方便比较控制效果，统一在振动位移约40mm时施加控制。

4.2.1常规PD控制实验结果

进行试验研究时，通过多次实验调整的方法确定以下较好的控制参数：k_p=2.8，k_d=6.4，信号由于采样和时间延迟等因素，移动相位10个采样周期。采用PD控制算法进行柔性机械臂振动主动控制试验研究，图10显示了柔性臂的常规PD控制振动位移曲线。

实验结果显示，臂的大幅值振动在前2个振动周期内就已经明显衰减，且电机的控制量相对较大。振动经过1.6S衰减至20%，对比自由振动4.5S的衰减时间，表明大幅值振动在短时间内得到了有效抑制;但是小幅值振动依然持续了较长时间，且经过长达6s的时间振动才被基本抑制下来，这也反映了常规PD控制的局限性所在。

4.2.2蚁群PD控制实验结果

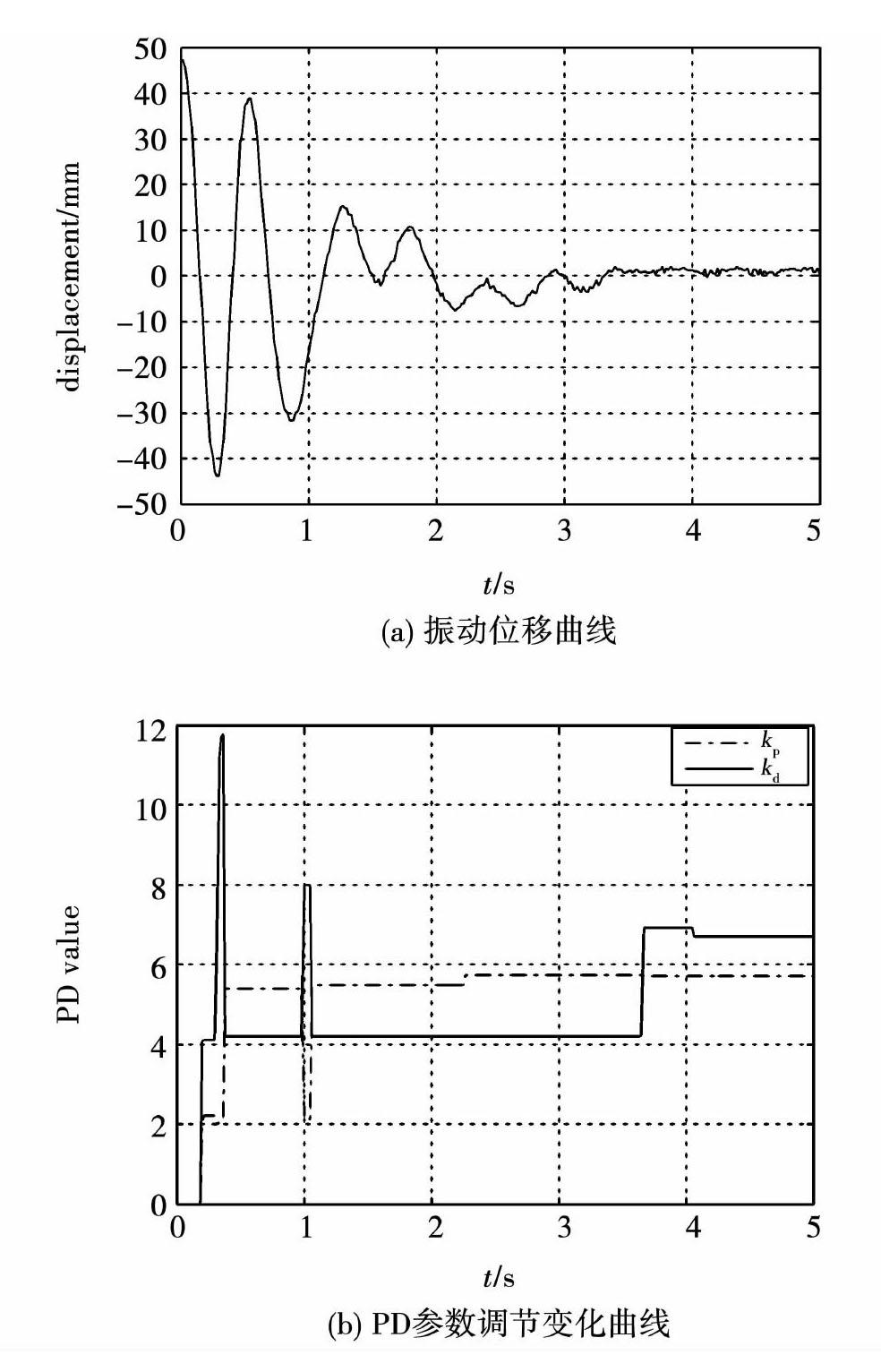
针对本实验平台，通过实验调试可以确定以下蚁群优化系统参数：信息启发因子α=1.3，期望启发因子β=5.0，贪心概率q_o=0.05，信息素蒸发常数λ=0.95，全局信息素更新系数k=10;另外限定k_p。的取值范围是[0，6]，k_d的取值范围是[0，12]，移相12个采样周期。图11显示了柔性臂的蚁群PD控制实验结果，其中图11（a）为振动位移曲线，图11（b）为PD参数的动态调整变化趋势。

实验结果显示，柔性机械臂的大幅值振动同样在前2个振动的振幅周期内明显衰减，而这种情况下电机的控制量也相对较大。振动经过1.6s后衰减至20%，表明大幅值振动的短时间抑制有效性。并且经过3.3S后振动基本被抑制下来，表明算法对于小幅值振动抑制同样具有较好效果，体现了控制算法的非线性特性。

控制过程中，PD参数值根据反馈的振动信息实时调整变化，反映了蚁群算法优化的效果。对比常规PD控制效果可知，蚁群PD控制在大幅值振动控制方面效果基本相近，但在小幅值振动控制方面具有明显的优越性。

4.3旋转振动控制实验结果

给伺服电机输入正弦电压信号，驱动柔性臂的中心刚体做简谐旋转摆动，设定摆动周期为10s，幅值约为15°，摆动一个来回。图12显示了当不施加任何控制效果时柔性臂自由振动信息，其中虚线代表了中心刚体的旋转角度位置。

由图12可见刚体的旋转会持续激励柔性臂的振动，且振动的整体偏向和刚体旋转方向相反，而当刚体旋向改变时，容易引起大幅值的振动。这种现象主要是由于传动和啮合间隙的存在，使得电机反转时产生冲击而造成的。

针对以上问题，采用本文提出的蚁群PD控制算法对臂的旋转振动进行抑制。其中蚁群优化系统参数和4.2.2节相同，设定k_p的取值范围是[3，15]，k_d的取值范圍是[6，30]，移相14个采样周期。图13显示了对柔性臂的旋转振动施加蚁群PD控制的实验结果，其中图13（a）为振动时域响应，虚线为中心刚体的旋转角度位置，图13（b）为PD参数的动态调整变化趋势。

实验结果表明，在刚体单向旋转过程中，臂有一定的和旋向反向的弯曲挠度，但是挠度几乎没有变化或者变化缓慢而不呈现出周期性，说明振动基本被抑制下来了;当刚体旋向发生改变时，臂的挠度会有较大变化从而产生振动现象，但是也能在较短时间内抑制下来;最后当正弦信号输入停止时，产生的振动亦可以在4个振动周期内进行完全抑制。综合而言，相比于旋转自由振动，施加蚁群PD控制后柔性臂的振动得到了明显的抑制。

5结论

本文利用双目视觉这种非接触式的测量方式研究了柔性臂的振动特性，由于双目三维重建可以在视场范围内直接获取特征点的三维坐标，避免了柔性臂姿态对振动检测的影响，体现出其对柔性臂大范围可达空间内的定点和旋转振动检测的优越性。然后利用蚁群优化算法对PD控制器的控制参数进行优化，并通过伺服电机驱动对柔性臂振动进行抑制。实验结果表明，基于蚁群优化参数的PD控制能够在5个振动周期内对柔性臂的振动进行有效抑制，相较于常规PD控制抑振效果有一定改善，并且旋转振动的抑制效果也比较显著，以此验证了蚁群PD控制算法在快速抑振上的有效性。