营养冲调粥流化床干燥特性及动力学模型的建立

李雨朋，赵一霖，赵城彬，吴玉柱，许秀颖，曹 勇，张 浩*，刘景圣*

（吉林农业大学食品科学与工程学院，小麦和玉米深加工国家工程实验室，吉林 长春 130118）

20世纪70年代以来，方便食品的销售量在全球范围内持续增加，目前在国际市场上已经占据主导地位[1]。方便食品在国外又称为快速食品或快餐食品，通常以谷物、豆类、畜类、水产、果蔬等为原材料，通过新设备工艺以及新技术进行加工、包装、贮藏，尽可能保留食物原本的营养和口感，生产出具有简单便捷、方便携带、价格适宜、安全卫生，能直接烹饪食用等特点的产品[2-3]。方便食品以其节省精力、有效提高生活效率等特点，逐渐成为人们日常消费的必需品，得到了广大消费者的青睐，市场潜力巨大[4-5]。而营养冲调粥就是方便即食食品中具有代表性的一种。

随着现今科技手段的发展，各种加工与贮藏的技术越来越完善，其中干燥越来越受到人们重视，干燥作为贯穿于科技发展的技术手段，已成为一种可以减轻产品质量、降低贮藏和运输成本并延长贮藏期的重要手段[6-7]。在方便食品的生产加工过程中，干燥是极为重要的一道工序，不同的传热方式对于食品原料有着不同程度的影响。传统干燥方式主要有热风干燥、微波干燥、真空干燥、冷冻干燥。热风干燥作为传统干燥方法，仍是目前最普遍使用的干燥技术[8-9]。但热风干燥由于物料长时间与高温空气接触，导致其色、香、味难以保留，维生素等热敏性营养成分或活性成分损失较大[10]。微波干燥加热速度快、效率高，但是由于物料组织差异导致加热不均匀，局部温度过高，易形成硬块，使得产品营养风味受到损失、品质难以保证；真空干燥以其干燥温度较低的特点，可以一定程度上保持食品原有的风味及营养，但传热速度慢、干燥周期较长；冷冻干燥后的物料能够保持原有的化学组成和物理性质，营养流失少，但生产成本过高，不能广泛采用。而流化床作为一种具有较高传热、传质系数，能够提高生产能力的干燥设备，其优点在于设备简单、物料与气体接触面积大、热传递好、干燥速度快、温度分布均匀，能够有效地避免物料局部过热[11]。国内外专家对胡萝卜[12-13]、大豆[14]、玉米粒[15]、苹果[16]、青菜[17]等农产品流化床干燥进行了研究，也有学者在胡萝卜[18]、枸杞[19]、山药[20]、椰蓉[21]、槟榔叶[22]、苹果片[23]等农产品的干燥方面建立了数学模型。杨历等[24]在干燥玉米时，通过建立回归数学模型验证了流化床干燥过程中水分变化的规律。Babalis等[25]针对不同进风温度，通过10 个数学模型指标进行评价，选取了最合适无花果干燥的动力学模型。而对于营养冲调粥这类方便食品加工方面的应用鲜有文献报道。在流化床干燥过程中，不同的风速、进风温度等工艺条件能够直接影响干燥速率和物料含水率，而建立数学模型对于预测不同时刻、不同工艺条件下流化床的干燥速率和物料含水率以及对其进行精准控制具有较为重要的意义[26]。随着科学手段的发展，数学模型的建立在农产品干燥等加工过程中应用越来越多。

本研究以双螺杆挤压出的营养冲调粥为原料进行流化床干燥实验，分别以干燥风速、进风温度、原料的含水量（加工过程中原料的加水量）作为干燥过程中失水特性的主要影响因素。通过建立流化床干燥营养冲调粥动力学模型，得到营养冲调粥干燥过程中含水率的变化规律，为营养冲调粥后续的加工条件提供理论依据。

1 材料与方法

1.1 材料

玉米粉、红豆粉、荞麦粉、小米粉、燕麦粉均为市售，以实验室自制配方按一定比例（玉米粉、红豆粉、荞麦粉、燕麦粉和小米粉质量比为3.5∶3.0∶2.0∶0.7∶0.8）均匀混合，经双螺杆挤压膨化、切割器切割得到颗粒状物料。

1.2 仪器与设备

FMHE 36-24双螺杆挤压机、FMFC 400流化床干燥机 湖南富马科食品工程技术有限公司；BK150型游标卡尺 上海申工量具有限公司；JE502型电子秤上海浦青计量仪器有限公司；BSA224S电子分析天平赛多利斯科学仪器（北京）有限公司；101A-3E型电热鼓风干燥箱 上海实验仪器厂有限公司。

1.3 方法

1.3.1 流化床干燥工艺

启动流化床装置，调节设备至实验所需条件，将烘干至恒质量的杂粮粉经双螺杆挤压机挤压膨化（挤压膨化过程中加水量分别16%、18%、20%、22%、24%）后，由切割器切割成颗粒状物料。挤压条件为螺杆转速150 r/min、杆筒温度140 ℃、喂料量15 kg/h、切割器转速600 r/min。将40.00 g（±0.1 g）物料均匀平铺到自制筛网中，确保物料均能有效进行传质。将筛网放入流化床内固定。在干燥过程中，每隔1、5、10、15、30 min快速取出物料称质量，记录不同干燥时间的物料质量后将物料放回继续干燥，参照GB 19640—2016《食品安全国家标准 冲调谷物制品》，干燥至冲调谷物制品含水量不超过10 g/100 g时停止。

1.3.2 物料粒径的测定

利用游标卡尺测量刚挤压出试样的直径，每份试样随机测定10 次，求其平均值作为试样的平均直径D/mm。

1.3.3 干基水分质量分数、水分比及干燥速率的测定

物料的绝干质量md采取恒质量干燥法，参照GB 5009.3—2016《食品安全国家标准 食品中水分的测定》测定，热风干燥箱温度设定为105 ℃。湿基水分质量分数是指湿物料中水分质量与湿物料总质量之比。干基水分质量分数是以绝干物料为基准的含水量表示法，系指湿物料中水分的质量与绝干物料质量之比，即水分与绝干物料的质量比。湿基、干基水分质量分数分别按式（1）、（2）计算。

式中：ω为试样初始湿基水分质量分数/%；mw为湿物料中所含水分的质量/g；m为湿物料的总质量/g；ωt为t时刻试样的干基水分质量分数/%；mt为试样干燥至t时刻的质量/g；md为试样经105 ℃恒质量干燥法干燥后的物料质量/g。

营养冲调粥干燥过程中水分比（moisture ratio，MR）按公式（3）计算。

式中：ωt为t时刻试样的干基水分质量分数/%；ωe为试样平衡时干基水分质量分数/%；ω0为试样的初始水分质量分数/%。

一般情况下，因试样的平衡干基水分质量分数ωe远小于ωt与ω0，通常可以忽略。因此，公式（3）可简化为公式（4）。

物料的干燥速率采用Falade等[27]的方法计算，如式（5）所示。

式中：vi为i时刻的干燥速率/（%/min）；ωi为i时刻样品的干基水分质量分数/%；ωt为t时刻试样的干基水分质量分数/%。

1.4 数据处理与分析

利用Origin 8.5软件进行绘图，采用MATLAB软件以及SPSS 19.0软件对营养冲调粥流化床干燥实验数据进行处理及回归拟合。

2 结果与分析

2.1 营养冲调粥流化床干燥条件及双螺杆挤压膨化条件对湿基水分质量分数的影响

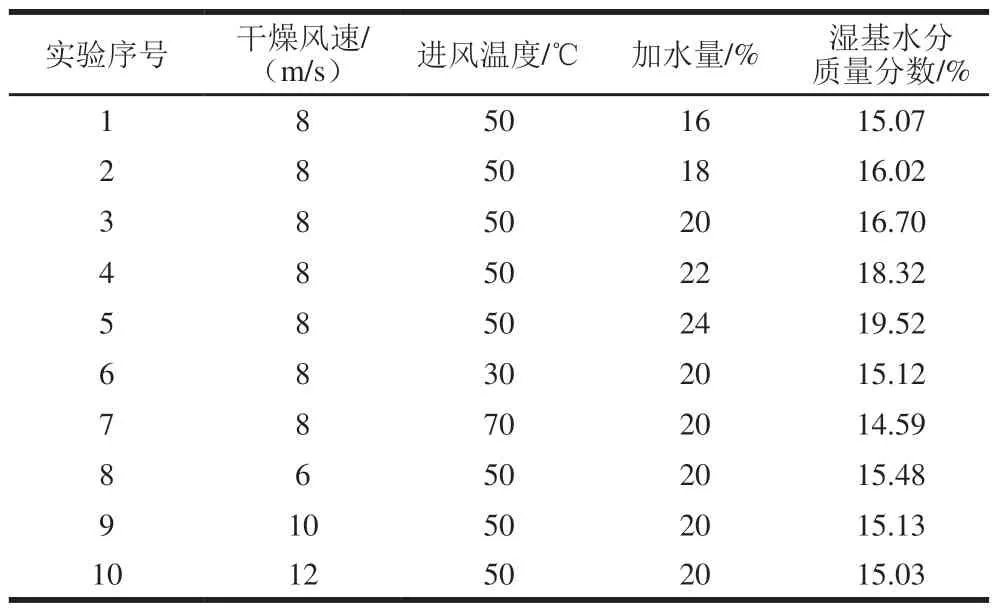
表 1 营养冲调粥流化床干燥方案Table 1 Fluidized bed drying scheme for nutritious reconstituted porridge

营养冲调粥流化床干燥条件及双螺杆挤压膨化条件对湿基水分质量分数的影响如表1所示。物料湿基水分质量分数与初始加水量有关，初始加水量越多，物料湿基水分质量分数越大；初始加水量不变，进风温度和干燥风速对物料湿基水分质量分数影响不明显。

2.2 营养冲调粥双螺杆挤压膨化加水量对挤压膨化和流化床干燥后物料粒径的影响

营养冲调粥物料的粒径大小同双螺杆挤压膨化过程中加水量有关。在流化床干燥过程中物料的粒径大小变化可以忽略不计（表2）。

表 2 不同加水量物料的粒径大小Table 2 Particle size of reconstituted porridges with different amounts of water addition

2.3 单因素对干燥特性的影响

2.3.1 加水量对营养冲调粥失水特性的影响

当物料装载质量40.00 g、干燥风速8 m/s、进风温度50 ℃时，薄层厚度为物料粒径大小（表2），不同加水量下营养冲调粥干燥曲线和干燥速率曲线如图1所示。

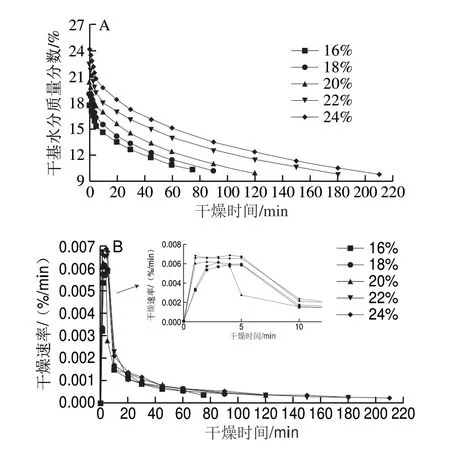
图 1 不同加水量下的营养冲调粥干燥曲线（A）和干燥速率曲线（B）Fig. 1 Drying curves (A) and drying rate curves (B) of nutritious reconstituted porridge with the addition of different amounts of water

由图1A可知，随着物料挤压膨化时加水量的增大，营养冲调粥的干燥曲线斜率逐渐增大，这一阶段为加速干燥阶段。物料挤压膨化时加水量越大，干燥速率越快，但干燥至安全含水率（10 g/100 g）所需的时间较长。主要原因是在干燥过程中传热和传质的条件一定时，初始含水量越高，物料内部的水分扩散速度越快，导致物料干燥速率越快，但因为初始湿基水分质量分数较高，相对的物料干基水分质量分数较高，干燥至安全含水率所需的时间较长；物料挤压膨化时加水量越小，干燥速率越慢，但干燥至安全含水率所需的时间却越短。主要原因是干燥过程中，湿基水分质量分数降低，物料内部的传递阻力增大，水分扩散速度降低，内部水分扩散至表面气化量少，会导致物料干燥速率较慢，但因为湿基水分质量分数较低，相对的物料干基水分质量分数也较低，导致物料干燥至安全含水率所需的时间反而越短。在干燥后期，干燥曲线趋于平缓，此阶段为降速阶段，表明流化床干燥脱水难度增加。因此，物料的湿基水分质量分数过高，所需干燥的时间过长，造成过多能耗损失，故挤压膨化过程中物料加水量为16%～20%较好。由图1B可知，营养冲调粥流化床干燥同传统干燥规律一致，可分为3 个阶段：加速、恒速及降速阶段。物料挤压膨化时加水量越大，流化床干燥加速阶段时间越短，进入恒速阶段所需的时间越少。干燥速率随着物料挤压膨化时加水量增大而增大。

2.3.2 进风温度对营养冲调粥失水特性的影响

当物料挤压膨化时加水量为20%、进风风速为8 m/s、薄层厚度为6.90 mm时，不同进风温度下营养冲调粥干燥曲线和干燥速率曲线如图2所示。

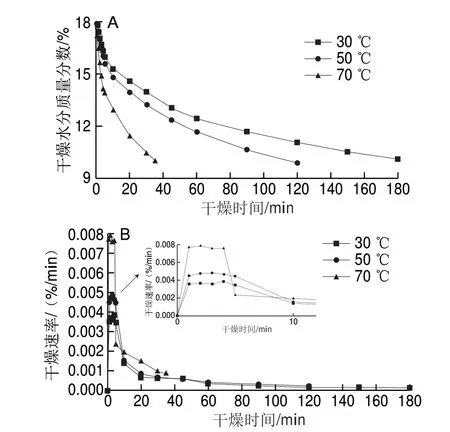
图 2 不同进风温度下的营养冲调粥干燥曲线（A）和干燥速率曲线（B）Fig. 2 Drying curves (A) and drying rate curves (B) of nutritious reconstituted porridge at different inlet air temperatures

由图2A可知，进风温度越高，营养冲调粥的干燥曲线斜率逐渐增大，这说明进风温度越高，物料表面的传热速率越快，物料内部的水分扩散速率越大，干燥物料的速率越快，干燥至规定含水率所需的时间也越短。反之，物料的干燥速率越慢，干燥至规定含水率所需的时间也越长。进风温度越高，流化床内部升温时间越长，持续保持温度的耗能越大，对物料的品质也有一定的影响；而进风温度过低、干燥周期过长不利于加工生产。所以干燥过程中干燥温度采用50～70 ℃左右较好。由图2B干燥速率曲线可知，进风温度越高，加热阶段干燥速率越大，恒速阶段转为降速阶段越快，原因是进风温度越高有利于加快干燥过程的传热和传质，提高物料表面水分蒸发的速率，从而缩短干燥时间。干燥后期速率逐渐降低至趋于平缓，是因为物料水分减少，导致流化床干燥脱水难度增加。

2.3.3 干燥风速对对营养冲调粥失水特性的影响

当进风温度为50 ℃、物料加水量为20%、薄层厚度为6.90 mm时，不同干燥风速下营养冲调粥干燥曲线和干燥速率曲线如图3所示。

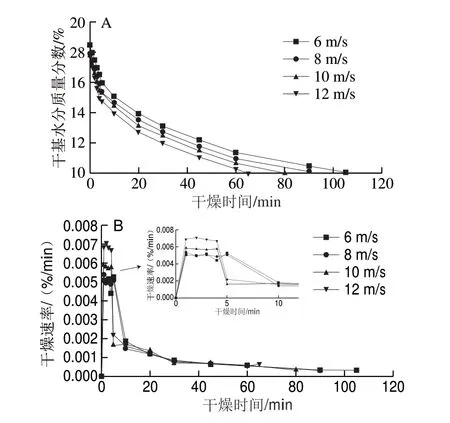
图 3 不同干燥风速下的营养冲调粥干燥曲线（A）和干燥速率曲线（B）Fig. 3 Drying curves (A) and drying rate curves (B) of nutritious reconstituted porridge at different airflow rates

通过图3A可知，随着干燥风速的增大，物料干燥曲线的斜率越大，干燥速率越大，这说明干燥风速越大，物料表面的对流传质越明显，加快了气体带走水分的速率，增大了有效水分扩散系数。在干燥后期，曲线趋于平缓，这是因为物料水分不断减少，内部水分扩散速度与表面水分气化速度达到平衡后，干燥速率随着干燥风速的变化而变化的效果明显降低，所以风速的变化对物料干燥前期的影响较为明显，而对干燥后期的影响不明显。最长干燥时间为105 min到达干燥终点。由图3B可知，干燥风速过低时，物料干燥速率变化不明显。干燥风速越高，物料干燥速率变化越明显。

2.4 干燥动力学模型选择

由图1～3可以得出，营养冲调粥流化床干燥过程中水分比MR与干燥时间t呈曲线关系，应选取以指数函数为基础函数的数学模型，目前，常用的农副产品流化床干燥的数学模型[28-30]有：单项扩散模型（式（6））、Lewis模型（式（7））、Page模型（式（8））。

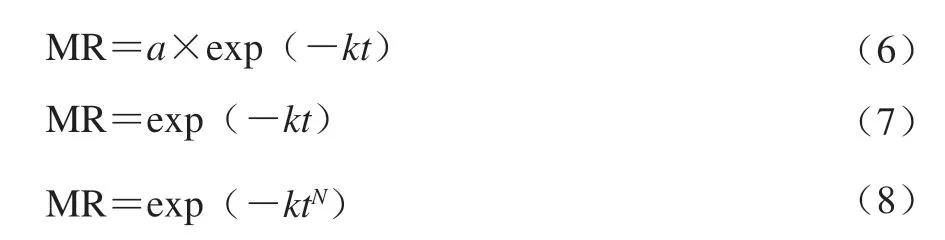
式中：a、K、N为模型参数。Lewis模型是单项扩散模型和Page模型的特殊形式，所以采用单项扩散模型和Page模型来模拟营养冲调粥的干燥过程[31]，因此，将公式（6）、（7）转化为线性模型，可得式（9）、（10）。

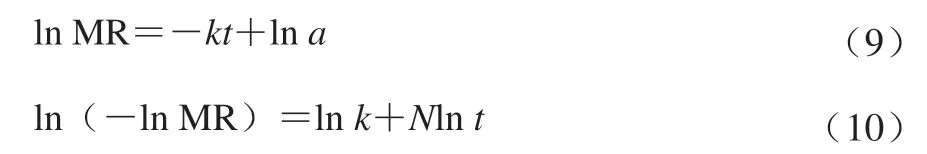
2.5 模型参数的确定

根据对实验数据的分析处理，绘制不同条件下营养冲调粥流化床干燥的－ln MR-t关系曲线和ln（－ln MR）-lnt关系曲线，如图4～6所示。

图 4 不同加水量下ln（－ln MR）－ln t（A）和－ln MR-t（B）关系曲线Fig. 4 ln(−ln MR) versus ln t (A) and −ln MR versus t (B) curves of nutritious reconstituted porridge with the addition of different amounts of water

对不同条件下营养冲调粥流化床干燥曲线的ln（－ln MR）-lnt和－ln MR-t进行线性回归，得到线性回归方程及相关系数如表3所示。营养冲调粥干燥过程中，在ln MR-t坐标系中相关系数在0.963 03～0.980 38区间变化，在ln（－ln MR）-lnt坐标系中相关系数在0.998 57～0.999 82区间变化。根据相关系数r得到，实验数据在ln MR-t和ln（－ln MR）-lnt两个坐标系中均有良好的线性关系。对相关系数r进行比较可知，在ln（－ln MR）-lnt坐标系中实验数据的线性拟合程度更好，而ln（－ln MR）-lnt是由Page模型转化而成，所以Page模型在本实验中更适合描述营养冲调粥干燥过程。令：

将式（11）、（12）代入Page模型则得到式（13）。

式中：T为进风温度/℃；v为干燥风速/（m/s）；H为加水量/%；a、b、c、d、e、f、g、h为待定系数。

运用MATLAB软件对实验数据进行处理，可得到营养冲调粥流化床干燥的各待定系数，进而求得其动力学模型为：ln（－ln MR）＝－4.064 63＋0.014 14T＋0.069 85v＋0.327 5H＋（0.570 96＋0.000 976 25T－0.009 68v－0.265 5H）lnt。

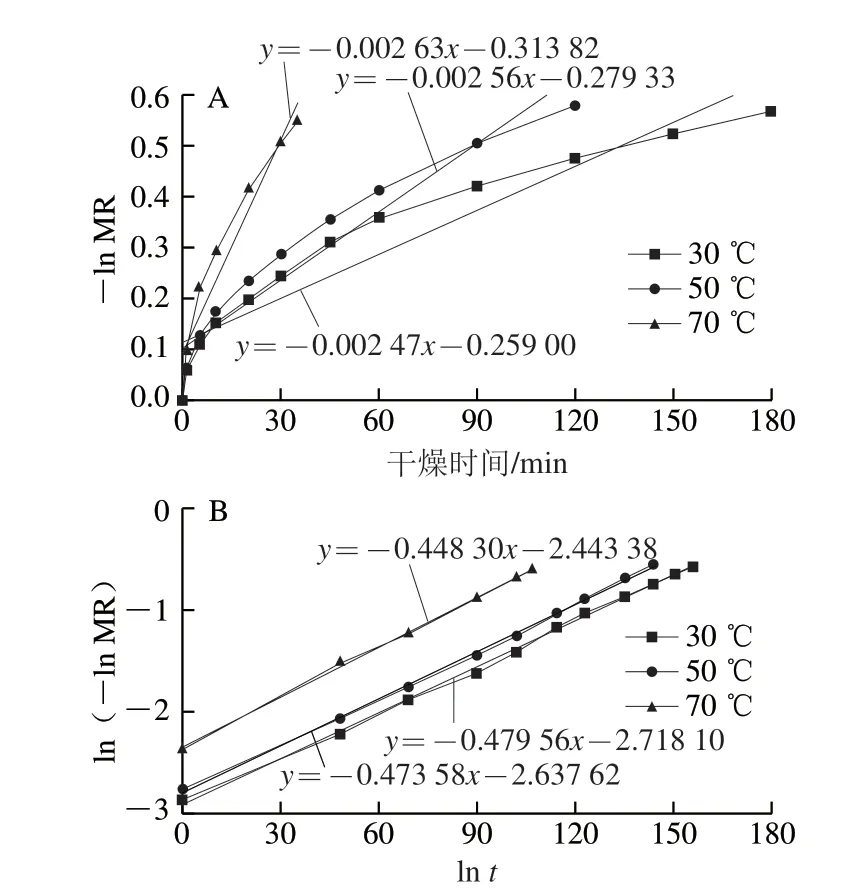
图 5 不同进风温度下ln（－ln MR）-ln t和－ln MR-t关系曲线Fig. 5 ln(−ln MR) versus ln t and −ln MR versus t curves at different inlet air temperatures

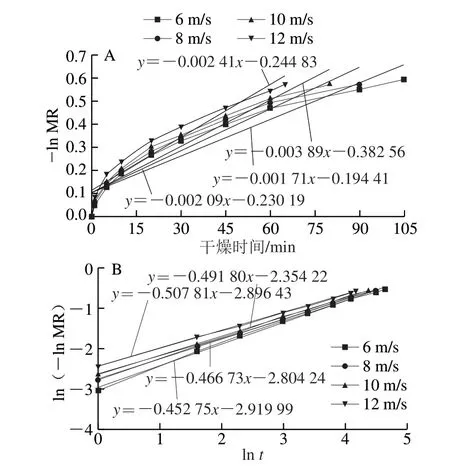
图 6 不同干燥风速下ln（－ln MR）-ln t和－ln MR-t关系曲线Fig. 6 ln(−ln MR) versus ln t and −ln MR versus t curves at different airflow rates

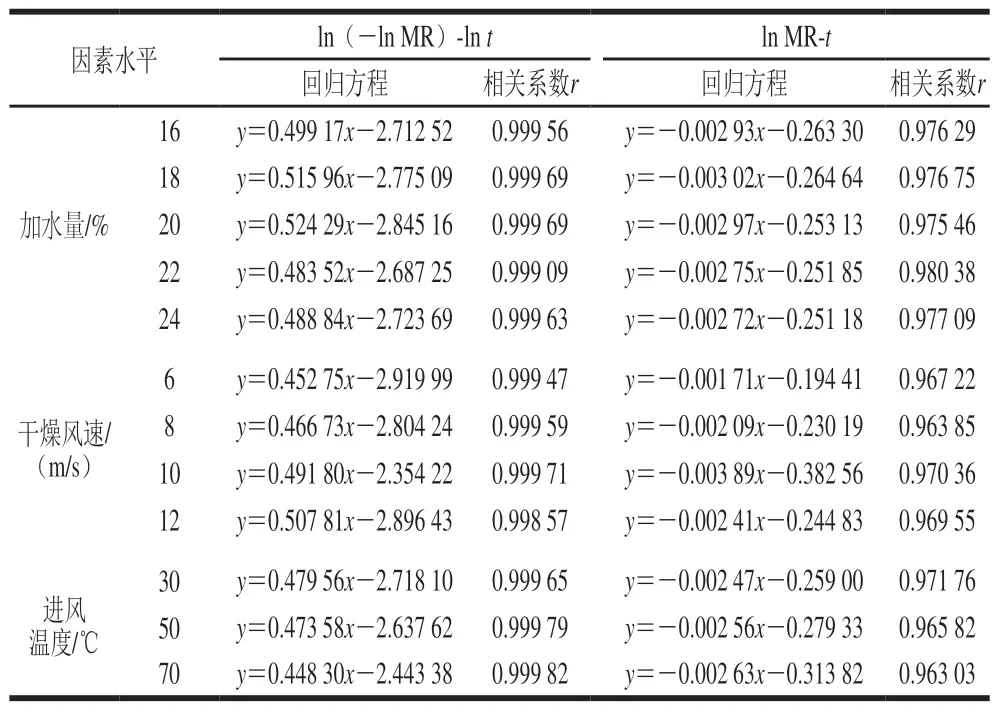
表 3 不同干燥条件下干燥曲线的线性回归方程及相关系数Table 3 Linear regression equations and correlation coefficients under different drying conditions

2.6 模型的统计验证

为了检验模型的拟合效果，对上述模型进行统计检验，检验结果见表4。模型方差分析中，F＝4 126.205（P＜0.000 1），模型的决定系数R2＝0.982 35，表明拟合效果好。因此，可将该拟合方程作为营养冲调粥的数学模型，利用此模型可以较为准确地预测在不同干燥条件下，营养冲调粥流化床干燥过程中干基水分质量分数和干燥速率。

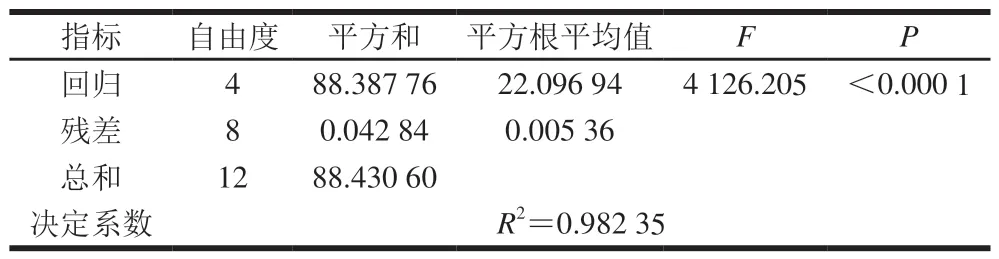
表 4 营养冲调粥流化床干燥拟合方程的方差分析Table 4 Analysis of variance of the fitting equation

2.7 动力学模型的验证

为了进一步验证拟合方程的拟合准确度，任意选取一组实验条件进行验证，实验条件为：加水量20%、进风温度60 ℃、干燥风速8 m/s。通过Page方程的拟合方程在上述条件下进行预测，对该组实验数据和预测数据进行比较。由图7可知，两条曲线基本一致，表明该拟合方程可以较好地反映营养冲调粥流化床干燥的规律，可达到准确预测的目的。

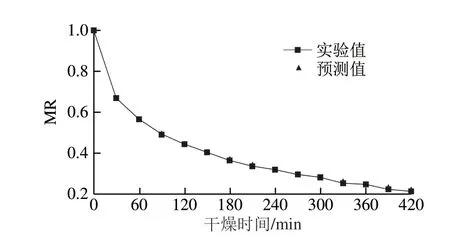
图 7 营养冲调粥流化床干燥数学模型验证曲线Fig. 7 Validation of the drying model

3 结 论

营养冲调粥流化床干燥方法同传统干燥规律一样，分为加速、恒速及降速3 个阶段。流化床干燥具有较高的传热和传质速度、干燥速率快、热效率高、结构紧凑、基本投资和维护费用低、便于操作等优点，更适用于营养冲调粥的干燥处理。

物料的加水量、进风温度和干燥风速对流化床干燥过程的影响均较为显著。进风温度越高，干燥风速越大，物料加水量越低，则干燥所需时间越短；反之，所需时间越长。

通过对3 种干燥模型线性回归分析的比较，Page模型更符合营养冲调粥干燥模型。利用MATLAB软件进行线性拟合，得到营养冲调粥流化床干燥的数学模型：ln（－ln MR）＝－4.064 63＋0.014 14T＋0.069 85v＋0.327 5H＋（0.570 96＋0.000 976 25T－0.009 68v－0.265 5H）lnt。

利用上述实验结果，可以较好地预测不同时刻营养冲调粥流化床干燥过程中的干燥速率和含水量的变化，为营养冲调粥流化床干燥工艺提供理论依据。