面向中短距光纤通信系统的多维自适应传输技术

唐明，陈曦

（华中科技大学光学与电子信息学院/武汉光电国家研究中心，湖北 武汉 430074）

1 引言

互联网技术的发展极大地提高了人们的生产生活质量，推动了高清视频、云计算、云存储、增强现实、虚拟现实等新型应用的快速发展。随着第五代移动通信的快速部署，网络扩容面临着迫切需求与极大挑战。目前，绝大多数的网络流量均直接或者间接地由光纤通信系统承载与转发[1]，这得益于其独特的容量优势。相比于微波通信仅几十兆赫兹的可利用带宽，目前光纤通信系统仅O+C+L 波段就具有近30 THz（1 THz=106MHz）的低损耗窗口。如此丰富的带宽资源保证了光纤的大容量通信能力。

1962年波长位于850 nm 附近的半导体激光器的研制成功[2]与1970年低损耗光纤的拉制成功[3]成为光纤通信系统诞生的2个标志性事件。在随后的几十年间，光纤通信系统经历了多次更新换代，传输指标由最初的45 Mbit/s速率和648 m的无再生传输距离[4]发展到现在最大可在17107 km 的单根单模光纤上支持51.5 Tbit/s 的速率[5]。短短的40年间，光纤通信系统的传输速率与距离积增大了3×1010倍以上。这一巨大的增速与多种技术的突破密切相关，如低损耗光纤、窄线宽半导体激光器、掺铒光纤放大器（EDFA,Erbium-doped fiber amplifier）、波分复用、相干接收、数字信号处理等。为应对不同的通信场景，现代通信系统也对器件和技术有针对性地取舍和优化。

根据思科（Cisco）[1]和贝尔实验室（Bell Labs）[6]的估计与预测，现在和未来的主要网络流量都将集中在以数据中心网络和城域网为代表的中短距离传输网络中。随着网络架构与业务的日趋复杂，传统的固定光网络面临极大的挑战。为解决这一问题，软件定义网络（SDN,software defined network）被提出[7]。通过分离数据层和控制层，SDN 可有效地利用网络资源，降低系统运营成本，提高网络的灵活性，这依赖于位于物理层的带宽可变收发机（BVT,bandwidth variable transponder）[8]。值得一提的是，中短距网络是典型的成本敏感场景，光电器件的有效带宽往往受限。而高速信号会占用更宽的带宽资源，导致信号承受更多的损伤，阻碍了系统进一步扩容。因此，研究面向中短距离网络的低成本大容量灵活光纤传输技术具有重要意义。

首先是对光纤传输方案的选型。根据收发机类型不同，光纤通信系统主要分为相干（coherent）和强度调制直接检测（IM/DD,intensity modulation and direct detection）2类方案。相干通信以较高的接收机灵敏度兴起于20世纪80年代，但真正引起研究热潮的是2005年发表的偏振复用数字恢复相位相干接收方案[9-10]。相干方案充分利用光纤信道中的物理维度，实现较高的频谱效率。并且相干接收机可恢复完整的光场信息，通过后端的数字信号处理（DSP,digital signal processing）技术，能有效补偿信道中的各类损伤[11]。但是相干调制与解调过程对光电器件要求苛刻，成本较高，且用于各类损伤补偿的DSP 增加了功耗，这些特性使相干技术多用于海缆等长距通信系统。与相干通信系统不同，IM/DD 系统伴随着光纤通信系统的兴起与发展。自20世纪70年代起，第一代光纤通信系统即采用基于IM/DD 的开关键控（OOK,on-off keying）调制格式[12]，受限于光纤色散，该系统需使用再生器对信号再生恢复，且相邻再生器间隔最高仅10 km。通过迁移波长至低损耗的1550 nm 附近，使用单模光纤以消除模间色散，以及应用色散补偿技术对色度色散有效管理，第四代IM/DD 系统最高可支持1000 km 传输[12]。即便如此，复杂的色散管理和有限的频谱效率让IM/DD 逐渐退出长距通信系统。但在中短距通信系统中，色散值较小不需要色散管理，IM/DD 方案得益于其结构简单、成本低廉、功耗低等优势，被广泛应用。近年来，研究人员也考虑将相干系统简化，在保留频谱效率优势的同时，降低系统成本与功耗，使其更加适用于中短距系统[13]。随着硅基集成技术的逐渐成熟，相干系统有望在将来应用于中短距系统，但固有的器件需求使其难以在短期内与IM/DD 系统竞争。

OOK 仍然是目前广泛应用的IM/DD 方案，但由于其仅有两电平，严重限制了频谱效率，这一问题在带宽受限的背景下尤为突出。使用高级调制格式提高频率效率，并与DSP 技术结合抑制信道损伤成为目前提升IM/DD 系统性能的主流方案[14]。具有代表性的高级调制格式包括以下3种：脉冲幅度调制（PAM,pulse amplitude modulation）、无载波幅度相位调制（CAP,carrier-less amplitude and phase modulation）与离散多音调制（DMT,discrete multi-tone）。PAM 在OOK 的基础上增加调制电平以提高频率效率。CAP 则将复数调制与频谱厄米共轭结合，实现高频谱效率的强度调制。PAM 和CAP 均可认为是单载波调制，而DMT 是由若干正交子载波组成的多载波调制方案，其中每个子载波均可进行独立的调制编码。因此，相比于单载波方案，DMT可根据信道条件或者网络业务的不同进行灵活的调整，以实现更高的频谱效率和更高的灵活度。以DMT 为基础开展面向中短距系统的灵活自适应传输研究具有天然的优势。本文将介绍几种基于DMT的高性能自适应传输方案，这几种方案以灵活的调制与编码为工具，从不同角度改进传统的比特与功率加载（BPL,bit and power loading）方案。

2 三维自适应调制编码

本节在BPL 基础上引入前向纠错编码（FEC,forward error correction）维度，实现三维自适应调制编码。FEC 不同的码率用于改善调制粒度，以应对复杂的信道变化。本节所提算法基于查找表，相比于传统BPL 算法——LC（Levin-Campello）算法[15]，显著降低了算法复杂度，也在一定程度上提高了传输速率。

基于DMT 系统最经典的自适应算法是BPL，即在不同子载波上加载不同的调制格式与功率。根据传输需求，此类算法可分为速率自适应（RA,rate adaptive）和裕度自适应（MA,margin adaptive）[16]。前者是在固定的信号功率条件下，最大化无误码传输的总速率；后者是在固定速率下，最大化信号功率裕度。本文着重关注RA 算法。目前，已有很多具体实现BPL 的算法，以Chow[17]、LC[15]等算法为代表，已被广泛应用于多载波通信系统中。得益于调制简单灵活，频谱效率高，QAM 是BPL 最为常用的调制方案。但普通QAM 的频谱效率以1 bit为间隔，调制粒度较粗糙，在处理复杂的信道变化时，BPL 需调整信号功率分布以匹配合适阶次的QAM，这种做法在一定程度上损失了信道容量。

另一方面，光纤通信系统以无误码传输为基础，一般认为误码率降低到10-15即达到无误码条件。前向纠错编码以一定冗余为代价大大放宽了误码率的限制。以常用的7%冗余的硬判决FEC 为例，纠错前误码率达到3.8×10-3时，即可认为达到纠错后无误码状态。一般传输方案使用固定的FEC，但本文注意到根据冗余量的大小，FEC 可对频谱效率微调，以改善调制粒度。本节方案利用这一特性，在原有BPL 基础上，增加对FEC 码率的调节，实现包括调制格式与功率在内的三维自适应调制编码。

2.1 最佳调制编码方案与SNR 关系

BPL 根据信道状态信息（CSI,channel state information）加载调制格式和功率，最常用的CSI为信噪比（SNR,signal-to-noise ratio）。给定误码率（BER,bit error rate）时，SNR 与调制格式间存在对应关系，这是实施BPL 的基础条件。与传统二维自适应算法类似，三维自适应算法需确定SNR 与最佳调制编码方案间的关系。首先确定QAM 调制格式的SNR 与纠错前BER 的关系，再由FEC 建立纠错前BER 与纠错后BER 的关系，即可得到SNR 与纠错后BER 的关系。在给定BER 限下，即可找到不同SNR 下速率最高的调制编码方案。下面将分析上述得到SNR 与BER 关系的具体过程。

根据矩形QAM 星座图的判决边界和噪声分布，Cho 等[18]严格推导出无FEC 时，加性高斯白噪声信道下SNR 与BER 关系，如式(1)所示。

其中，I和J表示QAM 的同相分量和正交分量的幅度个数，Υ表示信噪比，erfc 为误差函数，可表示为

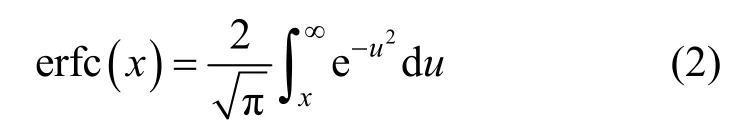
本节采用广泛使用的RS（Reed-Solomon）编码——RS（255,239）与RS（255,223）作为FEC的母码[19]。由于固定的DMT 帧结构，不同的调制格式对RS 编码需进行相应的缩短，具体组合如下：2QAM、2QAM-RS(64,48)、2QAM-RS(64,32)、4QAM、4QAM-RS(128,112)、4QAM-RS(128,96)、8QAM、8QAM-RS(192,176)、8QAM-RS(192,160)、16QAM、16QAM-RS(255,239)、16QAM-RS (255,223)，共12种备选调制编码方案。结合式(1)与RS编码纠错[19]，即可得到不同调制编码方案下SNR与BER 的关系。在不失一般性的前提下，为方便比较，取10-5作为纠错后BER 限来比较调制编码方案的优劣，以得到最佳调制编码方案。结果如图1所示，其中实线表示对应SNR 下选取的方案，虚线表示抛弃的方案。最左侧的起始点表示该方案满足纠错后BER=10-5时的最小SNR，即阈值SNR。需要注意的是，在实际仿真与实验中存在一定的SNR 估计误差，为提高算法的稳定性，阈值SNR（SNRth）需引入一定的裕度μ，则新的阈值SNR表示为

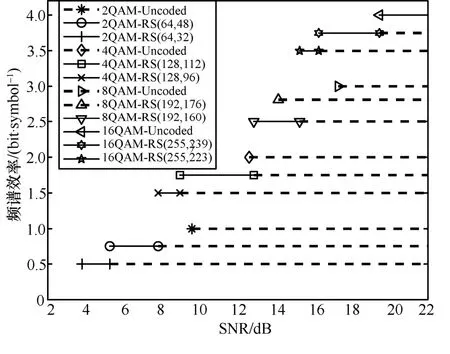
图1 加性高斯白噪声信道下解码后误码率为10-5时的最佳调制编码方案

此外，调制编码方案的频谱效率（单位为每符号信息比特，bit/symbol）和阈值SNR 间满足凸函数关系才能使加载方案达到整体最优[20]。8QAMRS(192,176)虽然可以在SNR 为14～15 dB 时表现出最好的性能，但由于其不满足凸函数关系，为提升加载算法的整体性能其也被抛弃。

2.2 三维自适应算法

根据图1所示的不同SNR 下最佳调制编码方案，在估计到各载波的SNR 后，通过简单查表的方法即可找到对应载波应加载的调制格式与FEC编码。例如，由图1可知，当估计的某一子载波SNR为11 dB 时，对应的调制编码方案为4QAMRS(128,112)，那么分配该子载波的调制格式为4QAM，FEC 编码为RS(128,112)。此外，本文发现虽然FEC 的引入减小了调制的粒度，但仍然存在一定的间隙，反映在图1中是相邻2种调制编码方案的阈值SNR 间存在间隙。当子载波SNR 处于该间隙中时，为满足BER 需求，仅能被分配具有较低频谱效率的方案。例如，4QAM-RS(128,112)的阈值SNR 为8.96 dB，上述例子中具有11 dB SNR 的子载波存在2.04 dB 的功率冗余。多载波系统的冗余功率累积会造成性能损失。因此，根据图1查表确定每个子载波的初始调制编码方案后，三维自适应算法计算总冗余功率与每个载波升级到相邻具有更高频谱效率的调制编码方案的频谱效率增益与所需的功率之比α。再将冗余功率依次分配到具有最大α的载波，用于升级该载波的调制编码。每次分配后，需对升级的载波重新计算α以寻找新的最大α。当载波已被分配到最大调制编码方案，停止该载波的方案升级（将α设置为0）。冗余功率被分配完毕时即完成三维自适应算法的流程。该算法细节可参考文献[21]。

2.3 仿真结果

为展示三维自适应调制编码算法的实际性能，本文搭建了仿真平台，结构如图2所示。发送的二进制信号首先经过串并转换以对应DMT 的不同子载波；再根据分配的FEC 编码对各个子载波进行独立编码，并映射到对应的调制格式上，进行QAM调制。QAM 信号的功率同样由自适应算法决定。在完成分配后，频域信号经过逆快速傅里叶变换（IFFT,inverse fast Fourier transform）转换到时域。为接收端进行帧同步与信道估计，需要在数据信号前添加训练序列。为避免有限的器件带宽和光纤色散引入的符号间串扰（ISI,inter-symbol interference），DMT 信号需要引入一定量的循环前缀，最后经过并串转换得到基带的时域信号。以上为发送端的DSP 算法流程，产生的时域信号被加载至任意波形发生器以完成模拟信号的产生，该信号经由低通滤波与放大后，驱动马赫曾德调制器（MZM,Mach-Zehnder modulator）将基带信号调制到光载波上，光载波由可调激光器产生。偏振控制器用于调整光载波的偏振态、降低MZM 的损耗。调制后的光信号经过单模光纤传输后，由EDFA 放大，并利用带通滤波器滤除带外自发辐射噪声。在光探测器进行光电转换前，由可调光衰减器控制接收光功率，以衡量不同系统状态下自适应加载算法的性能。

在接收端，模拟的电信号由数字存储示波器采样存储，用作后续的离线DSP 处理。信号首先进行帧同步，找到数据帧的帧头；再经过串并转换将串行信号转换为并行信号。去除冗余的循环前缀后，由快速傅里叶变换（FFT,fast Fourier transform）变换到频域进行后续的信道估计与均衡，得到恢复后的星座图。基于星座图可进行SNR 估计[22]，作为自适应算法的输入。最后，通过星座图解映射与FEC 解码将调制信号恢复为二进制信号，与发送信号对比计算BER。需要说明的是，因为自适应算法需要预先获取SNR，因此一般需要对信道的SNR预先估计，再根据估计得到的SNR 进行后续的调制、编码与功率的加载。详细的系统参数如表1所示，DSP 算法仿真程序使用Matlab 编写，光传输系统模型基于VPI Transmission Maker 仿真软件搭建，仿真结果如图3所示。

图2 DMT 仿真平台

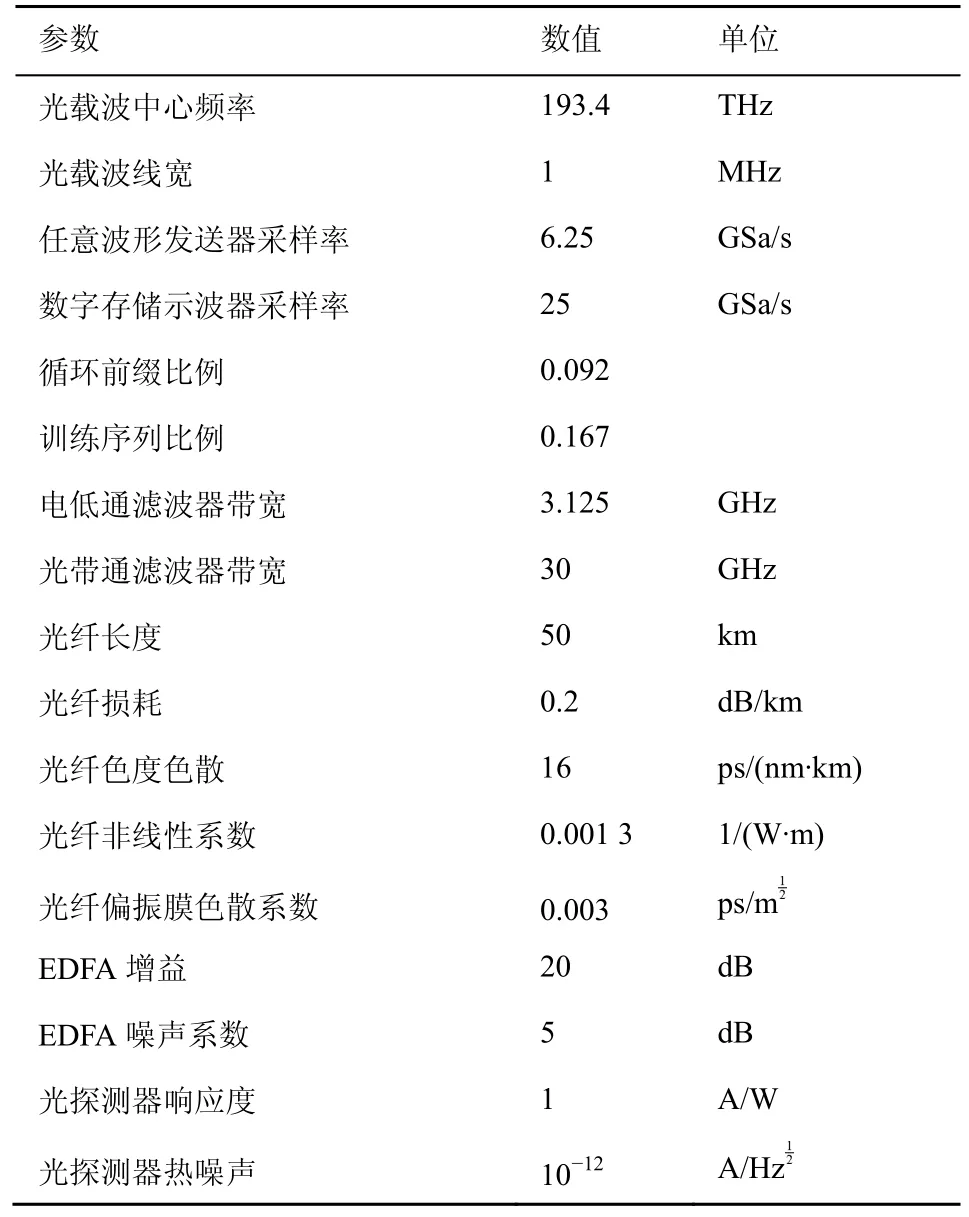
表1 DMT 传输系统模型参数

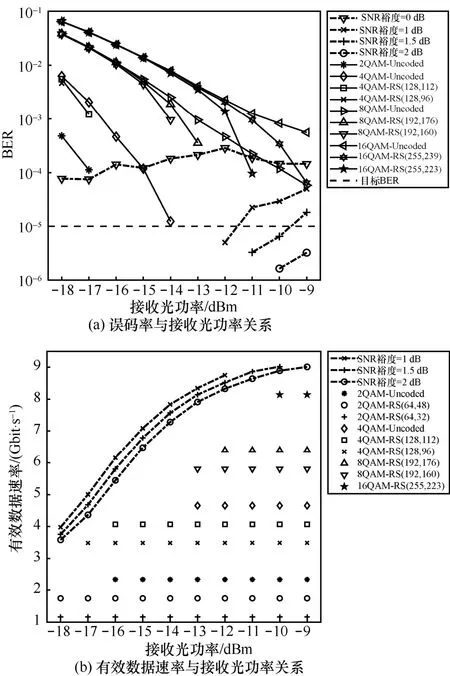
图3 仿真中不同接收光功率下三维自适应加载算法与传统方案对比

图3(a)为改变接收光功率时不同传输方案的误码率变化，未在图中标注的调制编码方案在图3(a)所示的接收光功率范围（-18～-9 dBm）内测量误码率均为0。可见传统方案的误码率随接收光功率的增大而减小，且调制编码方案的频谱效率越高，误码率也越高。而三维自适应算法可在较宽范围内保证BER 均在目标误码率以下，且SNR 裕度需根据接收光功率进行一定的调整，接收光功率越高时，SNR 裕度越大。图3(b)为达到目标BER 以下方案的有效数据速率，循环前缀与训练序列等冗余信息在速率计算中均被去除。可见普通调制编码方案的速率不随接收光功率而改变，但三维自适应算法使速率随着接收光功率的增大而增大，且对于任意接收光功率，自适应算法均实现了优于最佳普通方案的速率。当接收光功率为-14 dBm 时，SNR 裕度为1 dB 的自适应算法实现7.84 Gbit/s 的有效速率，是最佳普通方案的1.93倍。

为检验算法在带限信道中的性能，固定接收光功率为-10 dBm，改变电低通滤波器的带宽观察性能变化。仿真中，使用五阶贝塞尔滤波器模拟电低通滤波器，定义滤波器带宽系数为滤波器带宽3 dB 带宽与基带信号带宽的比例，当带宽系数为1时可认为无带限效应，仿真结果如图4所示。图4(a)展示的是BER 与滤波器带宽系数关系。可见随着滤波器带宽的减小，带限效应加重，普通方案的BER 随之上升。而在不同带宽下，三维自适应信号的BER 较为稳定，当SNR 裕度为2 dB时，BER 稳定于目标BER 以下。图4(b)展示的是有效数据速率与滤波器带宽系数的关系。同样地，图4(b)中只显示了达到目标BER 以下的方案。在滤波器带宽系数为0.4，即带宽为1.25 GHz时，普通方案都无法满足BER 需求。三维自适应信号能在图4所示的任意带宽下满足BER需求，速率也随带宽的增大而增大。图5展示了当滤波器带宽系数为0.5时的三维自适应算法加载细节。图5(a)为SNR 随子载波的变化，可见普通方案的SNR 随子载波索引（频率）的增大而平滑降低，而三维自适应方案呈阶梯状降低，与预计的SNR 变化趋势符合较好，此时的SNR 裕度为2 dB。图5(b)为三维参数的大小，调制格式由频谱效率表示，可见此时仅有16QAM（频谱效率为4 bit/symbol）与4QAM（频谱效率为2 bit/symbol），而码率有4种，使用的组合调制编码方案共5种，分别为16QAM、16QAM-RS(255,239)、16QAM-RS(255,223)、4QAM-RS(128,112)、4QAM-RS (128,96)。功率分配呈现阶段上升，幅度保持在±3 dB 以内，这一现象与经典的BPL 算法相似[17]。

图5 三维自适应算法的加载细节

三维自适应与二维自适应算法的性能比较结果如图6所示，二维自适应算法采用经典的LC 算法。图6(a)为三维自适应算法与采用不同编码的LC算法的速率对比。可见，三维自适应算法始终优于LC 算法。LC 算法在有RS 编码时速率随带宽增加上升更快。当带宽足够高时，LC 算法趋近饱和，而三维自适应算法的速率仍然在上升。这是由于在调制格式最高阶次的限制下，三维自适应算法可通过修改码率使速率上升，而LC 算法无法调节编码，速率趋近饱和。图6(b)比较了二维和三维算法的循环次数，用于表征复杂度。由于三维自适应算法采用查找表的方法，相比多次迭代的LC 算法，大幅降低了循环次数，使算法得以快速收敛。

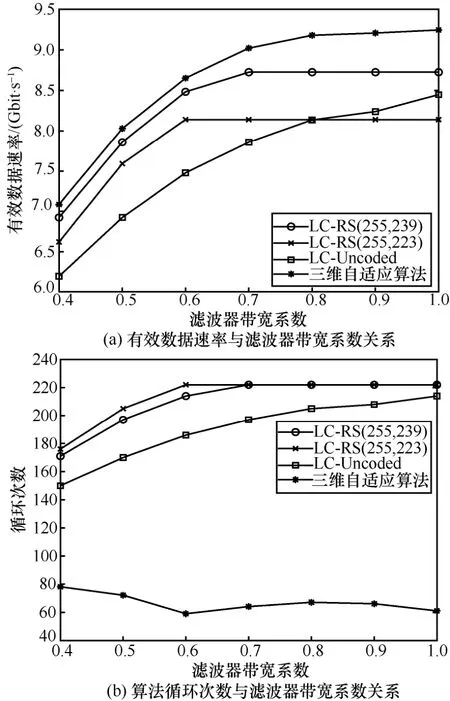
图6 不同滤波器带宽系数下三维和二维自适应算法性能比较

综上所述，三维自适应方案在不同的测量信道条件下均表现出优于固定调制编码方案与二维自适应方案的速率，并且算法复杂度远低于经典的二维自适应方案。本文研究团队同样开展了实验研究，结论与仿真结果高度符合，详情可参考文献[21]。

3 自适应分块预编码

本节介绍分块预编码方案。本节方案将可变的预编码块与调制格式分配结合，实现与LC 算法相近的速率，但具备更低的信号功率峰均比（PAPR,peak-to-average power ratio）。

虽然以DMT 为代表的多载波调制格式在灵活度与频谱效率上优于单载波调制格式，但由于各子载波间存在随机的相位匹配，使多载波信号在时域上有概率出现较大的峰值，增加了信号的PAPR。较高的PAPR 会降低驱动器的放大效率，并会在光纤传输过程中引入非线性效应，从而劣化信号质量。为抑制DMT 的PAPR，研究人员已提出了多种方法，具有代表性的方法有直接削波[23]、选择映射（SLM,selective mapping）[24]、部分传输序列（PTS,partial transmit sequence）[25]和预编码[26]等。直接削波法十分简单，即当信号的功率超出阈值时，将信号功率修改为阈值。削波法可以有效地降低PAPR，但由于该操作为非线性运算，导致频谱展宽并引入带内非线性噪声，一定程度上降低了信号质量。因此，削波的大小需要根据系统参数权衡。与削波法不同，其他3种方法属于线性运算，不会引入额外的噪声。但经典的SLM 与PTS 算法均需额外的开销，用于传输特定的相位序列降低了有效传输速率，并且在寻找合适的相位序列过程中需要进行大量的运算，消耗了大量的计算资源。预编码是一种扩频技术[27]，仅需在原有的调制数据上进行一次矩阵运算即可完成，而解码过程也只需一次逆矩阵运算。相比SLM 与PTS，预编码不仅不会引入额外开销，还具有更低的复杂度。此外，为实现最强的PAPR 削减能力，预编码矩阵常采用正交矩阵[27]。预编码方案的名称以预编码矩阵的类型而命名，如DFT-S（discrete Fourier transform-spread）方案使用DFT 矩阵[28]，CAZAC（constant amplitude zero auto-correlation）预编码方案[29]使用Zadoff-Chu 序列产生的CAZAC 矩阵，OCT（orthogonal circulant matrix transform）预编码方案[30]使用循环位移Zadoff-Chu 序列生成的OCT 矩阵。此外，研究人员发现，在应用预编码方案后，即使在衰落信道中，经过解码的各子载波具有相近的SNR 分布，这显著提升了信号在衰落信道中的性能[29,31]。由于各项明显的优势，预编码被广泛应用于多载波通信系统中。

本节从理论上推导出预编码的SNR均衡原理[32]，并基于此，研究多分块预编码与自适应调制技术相结合的方案，提出一种自适应分块预编码（APP,adaptively partitioned precoding）算法，以同时实现信号PAPR 的抑制和总传输容量的提升。

3.1 噪声均衡

其中，Xm和Ym分别表示预编码前和预编码后的调制信号，维度为表示预编码矩阵，维度为Nm×Nm。是正交矩阵，若DMT 使用的循环前缀足够长，保证接收信号无载波间串扰，那么接收信号可表示为

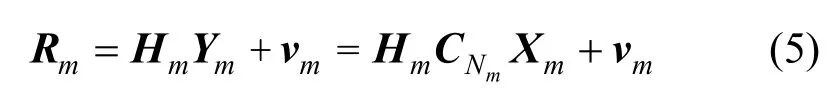
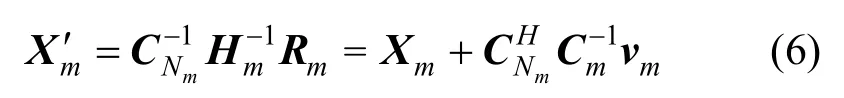
那么第i个子载波的噪声功率为

其中，cmn表示预编码矩阵中第m行第n列元素，且满足。考虑到各子载波的噪声独立分布互不相关，式(7)可写为

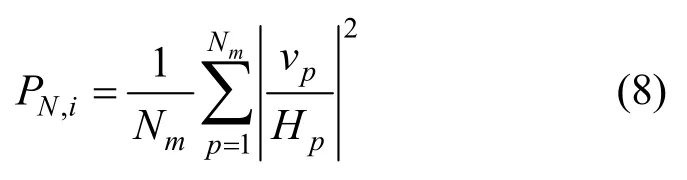
即预编码块内任意子载波的噪声功率是该预编码块内所有子载波噪声的平均。因此，若不修改信号功率，该预编码块内的SNR 近似相同，从理论上证明了正交预编码矩阵具有SNR 均衡的效果。

3.2 自适应分块预编码算法

传统的预编码方案对所有子载波使用同一预编码矩阵编码。由3.1节可知，所有子载波具有相近的SNR，因此所有子载波仅分配一种调制格式。这限制了调制格式分配的自由度，导致其传输容量无法与传统的BPL 算法相媲美。本文介绍的APP算法用于解决传统BPL 算法较高PAPR 和预编码方案传输容量较低的问题。具体而言，需解决划分预编码块与分配子载波调制格式这2个问题。

为与BPL 公平对比，本节仅考虑所有调制方案采用相同的FEC 编码，即使用标准的7%硬判决FEC 限3.8×10-3作为解码前BER。首先，采用与第2.1节类似的方法，得到最佳调制格式。如图7所示，每段线的左侧表示阈值SNR。在已知载波SNR时，即可根据图7得到对应的调制格式。

图7 加性高斯白噪声信道下使用硬判决FEC 的最佳QAM 调制方案与SNR 关系

基于图7所示查找表，APP 算法步骤可描述如下。详细步骤可参考文献[32]。

步骤1估计所有子载波SNR，并将所有子载波按照按SNR 由高到低排序。

步骤2从具有最高SNR 的载波开始，按步骤1的载波顺序，逐渐增加第一预编码块中载波数量，直到该分块的均衡SNR 第一次达到图7所示的某一调制方案的阈值SNR，将该调制方案分配给该分块内所有子载波。

步骤3增加新的预编码分块，该分块的子载波由上一分块后第一个载波开始，仍按步骤2原理依次增加子载波数目，直到第一次达到某一阈值SNR，并分配对应的调制格式。重复此步骤，直到所有载波均被分配到预编码块中，或剩余载波的SNR 低于最低阈值SNR。

步骤4最后一个预编码分块的均衡SNR 可能大于最近的阈值SNR，即存在冗余信号功率。将此冗余信号功率依次加载到具有最大信息比特增益的子载波上，提高该载波的频谱效率，直到所有冗余功率分配完毕。

3.3 实验验证

高速传输信号往往占据较宽的频谱范围，这意味着信号在光纤中传输会累积更多的色散。对于普通的IM/DD 系统而言，大色散会导致信号发生频谱选择性衰落[33]，严重减小可利用带宽资源，限制传输容量。频谱衰落的原因是色散引入的相移破坏了强度信号2个边带的频谱共轭对称条件，在功率探测过程中，2个边带发生拍频生成余弦项，导致频谱被余弦包络切割[12]。单边带调制是避免色散引入的频谱选择性衰落的有效手段[33-34]，通过消除其中一个冗余边带，在直接探测过程中避免了双边带拍频，从而避免余弦项的产生。与双边带信号不同，单边带信号属于复数信号，无法通过传统的强度调制生成。实现单边带调制一般有2种方法。一种是采用IQ 调制器进行复数调制，生成单边带信号。但相比于普通的马赫曾德强度调制器，IQ 调制器由2个马赫曾德调制器和一个相位调制器组成，成本大幅提升，偏置点控制也更加复杂。另一种方法是独立调制马赫曾德调制器的两臂。这一过程可近似为复数调制，从而以相同的调制器成本即可产生单边带信号[33]。为在高速信号中检测分块预编码性能，本文将基于单边带调制直接检测系统开展研究。

实验模型如图8所示，发射端的DSP 流程与图2中类似，主要区别是在IFFT 前引入了预编码。基带数字信号导入任意波形发生器生成模拟信号，采样率为40 GSa/s。经过电放大器放大后分别驱动双驱马赫曾德调制器的两臂，当两路信号满足互为希尔伯特变换关系时，即可产生单边带信号。可调衰减器1控制入纤功率为4 dBm。标准普通单模光纤长度为50 km 或80 km。在接收端前，通过图8的虚线框内器件组合控制信号的光信噪比（OSNR,optical signal-to-noise ratio），并由光谱仪测量OSNR大小。在进入光探测器前，可调衰减器3控制接收光功率固定在-1 dBm。由于该光探测器响应度较低（0.45A/W），故在其后添加电放大器。然后由数字存储示波器采样存储放大后的信号，采样率为80 GSa/s。接收端DSP 也与图2类似，不同的是在信道估计与均衡后添加解预编码操作，用于恢复QAM 信号。

优化调制器的调制深度后，比较不同光纤长度下APP 算法与LC 算法的性能。为公平比较，2种算法的信号平均功率保持一致，而非峰值功率一致，结果如图9所示。可见两者速率几乎一致，且BER 均低于FEC 限，可实现无误码传输。据本文调查所知，文献[32]是预编码方案第一次达到BPL算法的速率。

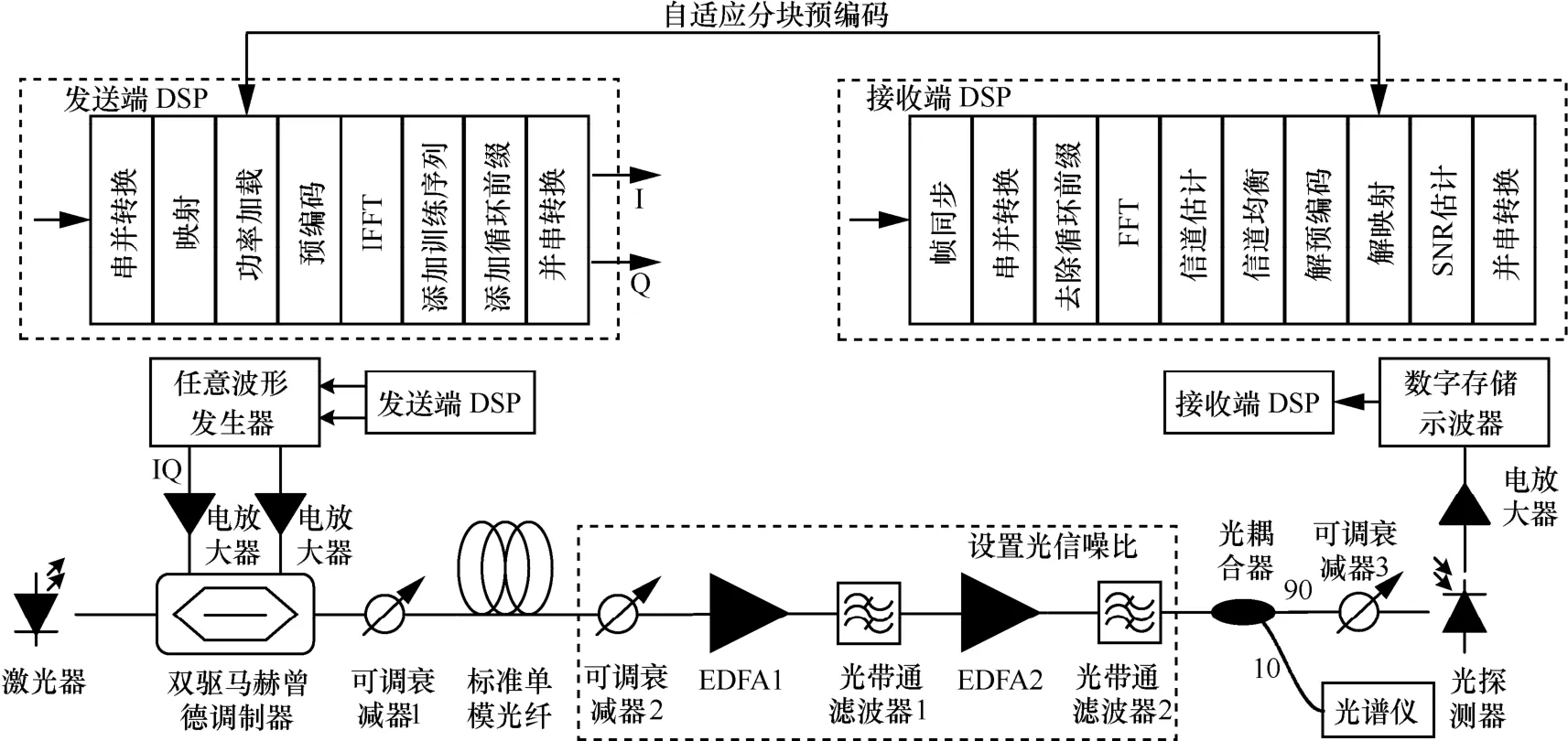
图8 面向自适应分块预编码DMT 的单边带调制直接检测传输系统模型

此外，本文还对比了LC 与APP 的PAPR 性能。由于时域DMT 信号存在随机性，因此一般采用互补累积分布函数（CCDF,complementary cumulative distribution function）表示PAPR 性能，具体含义为一段时间内，具有高于某一PAPR 值（PAPR0）的DMT 符号个数占总DMT 符号个数的比例。如图10所示，当CCDF 为10-3时，LC 的PAPR 在13.7 dB左右，与传输距离无关。而APP 的PAPR 随传输距离而波动，但均低于LC 的PAPR，最高可削减2 dB PAPR，这意味着相比于LC，当信号峰值功率归一化时，APP 可能实现最高2 dB 的SNR 提升。

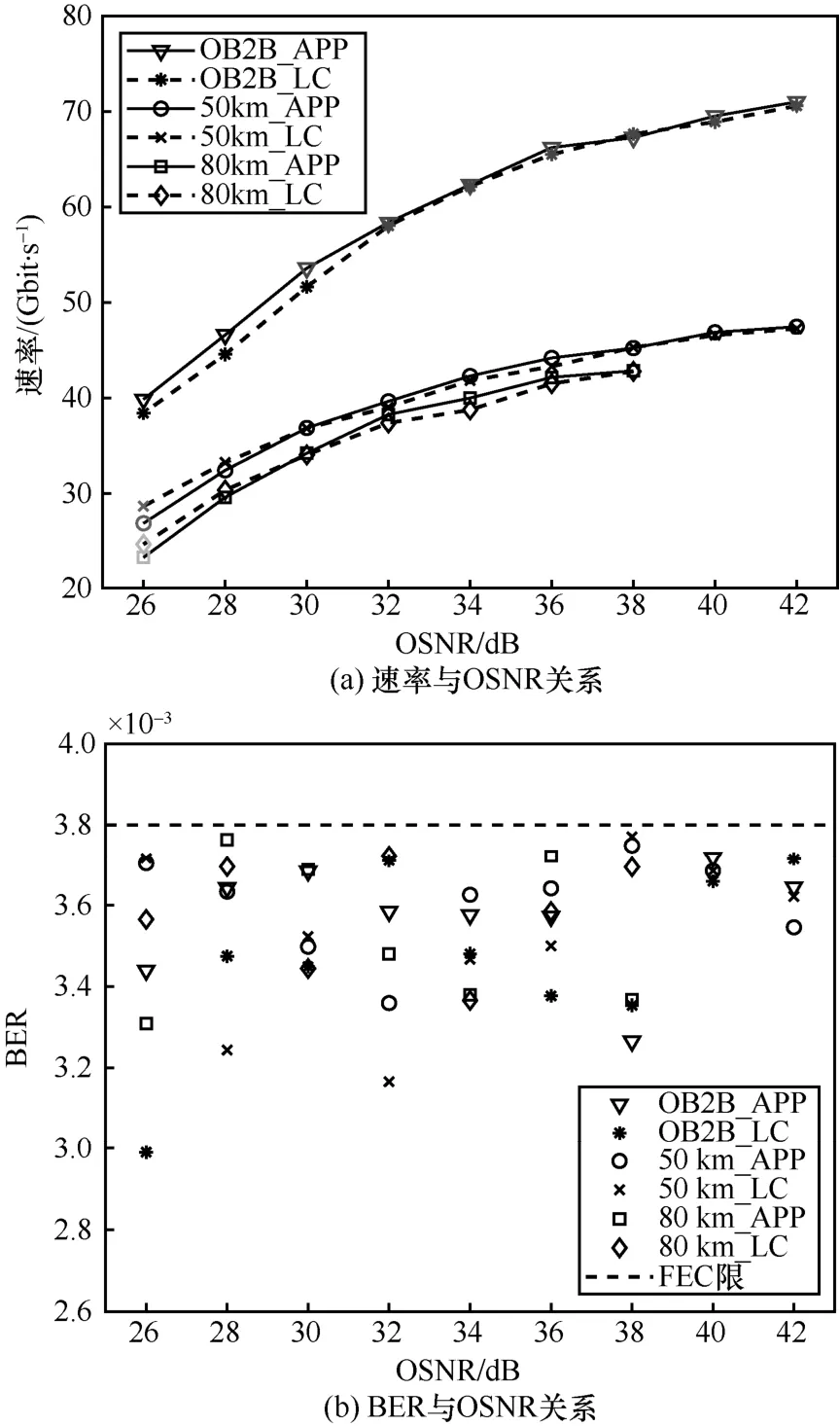
图9 APP 与LC 传输性能对比

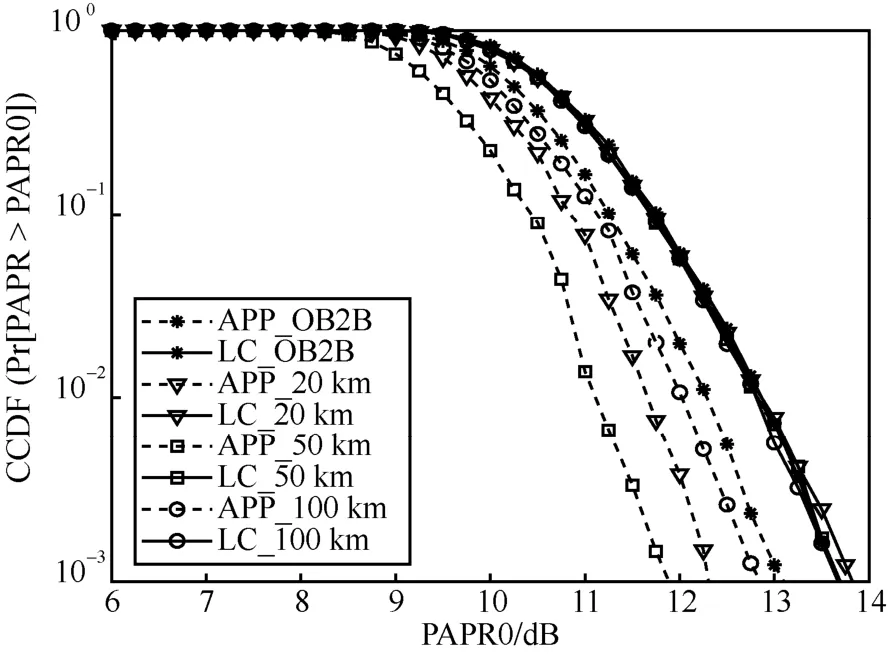
图10 APP 和LC 的PAPR 性能对比

进一步地，图11展示了2种自适应算法的分配细节。此时APP 分配3个预编码块，每个编码子集内一般仅有一种调制格式，但子集3是例外，其包含2种调制格式，这是由于冗余功率分配到对应的载波提高了调制比特数。LC 和APP 算法的估计SNR与预计SNR 均符合较好，但LC 的SNR 波动更为剧烈，APP 的SNR 变化更为稳定。这是由于信道随时间波动，LC 每个载波独立调制，因此受波动影响较大，而处于一个预编码块内载波的噪声被均衡，抵抗信道波动能力较强。此外，APP 算法仅需离散的几个功率值分配，LC 则需要连续的功率加载。

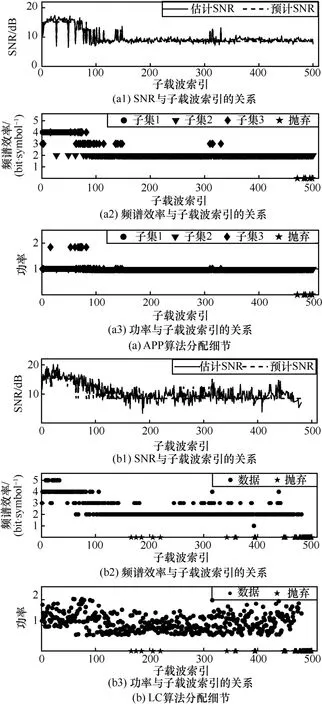
图11 光纤长度为50 km 与OSNR 为32 dB 时APP 和LC 的分配细节对比

综上所述，本文研究了预编码的噪声均衡原理，基于此原理提出了自适应分块预编码（APP）算法。采用灵活分块预编码的APP 算法可达到与LC 相近的速率，且相比于LC 算法，APP 最高可削减2 dB 的PAPR，理论上可提高2 dB 的SNR。此外，得益于预编码的噪声均衡特性，载波的SNR波动被预编码抑制，APP 算法具有更强的抵抗信道变化的能力。

4 自适应分块熵加载

本节在正交幅度调制（QAM,quadrature amplitude modulation）基础上引入概率整形（PS,probabilistic shaping）技术。比起普通 QAM，PS-QAM 实现了整形增益与近乎无限精细的调制粒度，更适合自适应加载算法，但同时也提高了复杂度。本节提出以预编码块为单位实施PS-QAM 分配的熵加载算法，在抑制复杂度提升的同时大幅提高传输速率，比LC 算法有9%的速率提升。

光纤信道一般由放大器的自发辐射噪声占据主导，可近似认为是加性高斯白噪声信道。根据香农定理，在加性高斯白噪声信道中，当信号服从高斯分布时，可以逼近信道的香农极限[35]。而普通QAM 属于均匀分布信号，距离香农极限存在间隙，并且无法通过FEC 编码弥补。在高SNR 处这个间隙值约为1.53 dB[35]。为弥补这一局限，基于分布匹配（DM,distribution matching）的概率整形（PS,probabilistic shaping）技术被提出[36]。通过结合概率幅度整形（PAS,probabilistic amplitude shaping）与恒定成分分布匹配器（CCDM,constant composition distribution matcher），使QAM 的不同星座点的概率分布贴近离散高斯分布或麦克斯韦玻尔兹曼（MB,Maxwell-Boltzmann）的概率分布，构成PS-QAM，实现逼近香农极限的能力。实用的PS-QAM 自2015年被提出以来[36]引起了研究热潮。由于良好的兼容性，PS-QAM 被迅速应用到单载波相干通信系统[37]。实验表明，相比于普通QAM，PS-QAM 可提高15.5%～34%的传输距离[38]。除贴近香农极限这一优点以外，通过调节概率分布，PS-QAM 可实现近乎无限精细粒度的频谱效率调节。这一特性非常适合于通过自适应加载以匹配不同的信道。在文献[39]中，研究人员研究在多载波系统的不同载波上加载不同概率分布的PS-QAM，实现比单载波系统更高的频谱效率。概率分布不同，PS-QAM 的信息熵（information entropy）也不同。参考传统的比特与功率加载，上述多载波系统加载多种PS-QAM 的做法也称作熵加载（EL,entropy loading）[39]。由于PS-QAM 出色的性能，它很快被引入IM/DD 系统中[40-41]。由于DMT 是IM/DD 方案中易于适配高级调制格式的解决方案，因此PS-QAM 常与DMT 组合使用。得益于PS-QAM 的整形增益，基于DMT 的熵加载可以实现比使用普通QAM 的传统自适应调制编码算法更强的性能。

另一方面，PS-QAM 也带来了复杂度的巨大提升。相比于普通QAM，PS-QAM 需要额外的DM和逆 DM。若熵加载针对每个载波独立加载PS-QAM，则DMT 需要与数据子载波数相同的DM与逆DM（一般为几百对），这将给硬件带来极大的负担，几乎无法在实际系统中实现。而根据第3节中的结果，经过分块预编码，每个独立分块内往往仅有一种调制格式。由于预编码块个数有限，则加载的PS-QAM 也将远小于子载波的数目，这将大幅降低熵加载的实现复杂度。自适应分块预编码与熵加载结合可以在降低熵加载复杂度的同时，利用PS-QAM 的高频谱效率实现高速自适应调制编码传输。

4.1 自适应分块熵加载算法

与使用普通QAM 的自适应加载算法相同，熵加载算法需要确定最佳PS-QAM 与SNR 间的关系。由于PS-QAM 的星座点概率分布不再是均匀的，PS-QAM 频谱效率的计算方法与普通QAM 并不相同。互信息量（MI,mutual information）或一般互信息量（GMI,generalized mutual information）常用于计算PS-QAM 在不同信道条件下的最大可实现频谱效率。但这是基于理想FEC 的条件下，因此MI 与GMI 不能体现PS-QAM 的实际性能。为与普通QAM 公平比较，本节基于相同的现有FEC，比较不同QAM 的每符号信息比特。使用6.25%Staircase-FEC 与20% LDPC 的级联码作为FEC，为实现无误码传输，一般信号的归一化互信息量（NGMI,normalized generalized mutual information）应大于0.858[42]。以无误码为条件，通过在加性高斯白噪声信道中的蒙特卡洛仿真，得到普通QAM 与基于不同星座图的最佳PS-QAM 和SNR 的关系。

如图12所示，由于较粗的调制粒度，普通QAM的每符号信息比特随SNR 呈现阶梯型增长，而得益于连续的概率分布调节，PS-QAM 的每符号信息比特实现连续的增长。相比于第2节中使用FEC 有限地改善调制粒度，PS-QAM 从根本上解决了这个问题。且在相同每符号信息比特下，PS-QAM 比普通QAM 需要更低的SNR，这个SNR 差是由PS 的整形增益带来的。特别地，PS-QAM 中，低阶星座图在低SNR 时可实现更高的频谱效率，那么根据SNR 范围选择星座图可实现更高的SNR 增益。当每符号信息比特为2.5 bit 时，选择PS-16QAM 比PS-64QAM 与PS-256QAM 更佳。而当每符号信息比特为4 bit 时，PS-64QAM 是最好的选择，因为此时已超出PS-16QAM 上限，且PS-256QAM 需要更高的SNR。

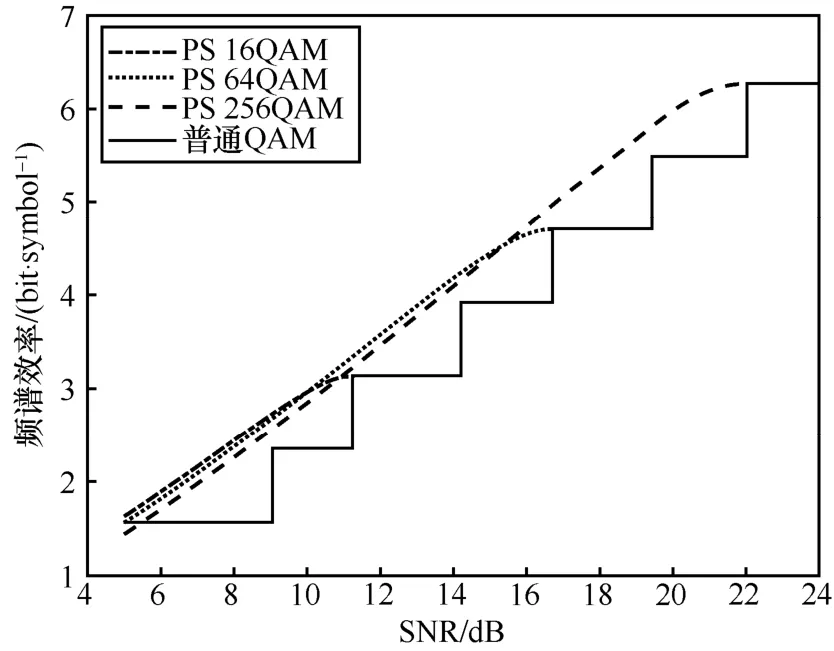
图12 加性高斯白噪声信道中NGMI 小于0.858时的最佳PS-QAM 与普通QAM 与SNR 关系

参考3.2节的算法，根据图12的关系曲线，分块预编码算法步骤可描述如下。

步骤1估计所有子载波SNR，并对所有子载波按照SNR 大小由高到低排序。

步骤2设定预编码块数目，基于步骤1排序，所有预编码块按顺序相邻放置。通过移动相邻预编码块的分界载波，遍历所有载波组合。根据3.1节描述的SNR 均衡原理与香农容量定理，计算所有载波组合的总容量。

步骤3选择总容量最高的预编码分块组合，根据最佳分块的SNR 加载PS-QAM，并恢复子载波索引。

由于步骤2中，在指定的预编码块数目下，此算法遍历了所有相邻预编码块，并在其中选择了实现最高容量的组合，因此称之为最佳分块预编码（OPP,optimally partitioned precoding）熵加载。在对子载波按SNR 排序后，根据蒙特卡洛仿真，在噪声功率不一致时，相比于不相邻放置，相邻放置预编码块可取得更高的容量，因此OPP 不考虑不相邻放置子载波的情况。描述步骤2过程的示意如图13所示，以8个子载波，指定预编码块为2为例。由于步骤1中对子载波按SNR 降序排列，当预编码块1中子载波数目逐渐增多时，根据式(8)可知，均衡的SNR 逐渐降低。同时，对于预编码块2而言，高SNR 载波转移至预编码块1中，其均衡SNR 也逐渐降低。通过移动相邻预编码块间的分界点，即可遍历所有相邻分块方式。再根据每种分块方式的均衡SNR 与香农公式即可计算总容量，并选出实现最大总容量的分块方式。对于多预编码分块而言，由于子载波仍然是相邻放置，相比于图13的唯一不同点即增加了预编码块分界点个数。但由于步骤2中采用遍历的方法，随着预编码分块数目的增大，复杂度将随之以指数级增加。

图13 OPP 算法遍历过程示意

另一种常见的分块方法是对子载波按照频率顺序等间隔分割。此方法不考虑实际的信道特性，仅与子载波数与设定的预编码块有关，称之为等间隔分块预编码（EPP,equally partitioned precoding）。相比于OPP，EPP 直接根据子载波数目与指定的预编码块数，得到预编码块的分块样式，复杂度为O(1)。详情也可参考文献[43]。

4.2 实验结果

本实验采用与3.3节相同的单边带传输系统，主要区别在于将评价指标由OSNR修改为接收光功率[43]，并且由于PS-QAM 的引入，DSP 略有不同，如图14所示。

图14 分块熵加载DMT 的发送与接收DSP

由于OPP 的复杂度随预编码分块的个数增大而迅速增加，首先研究预编码分块数对净速率的影响。经过80 km 标准单模光纤传输后，图15表示净速率与预编码分块数目的关系。可见当分块数大于或等于3时OPP 的净速率趋于稳定，这也说明仅需3种PS-QAM 即可。固定预编码分块数为3时，比较EPP、OPP 与传统的LC 算法性能，结果如图16所示。可见EPP 与OPP 均远优于LC 算法，并且OPP 针对信道特性进行合理的分块，实现比EPP 更高的速率。当净速率为60 Gbit/s 时，OPP相比于LC 实现了4.4 dB 的接收机灵敏度提升，并且在接收光功率为-15 dBm 时，OPP 实现9%的速率提升。

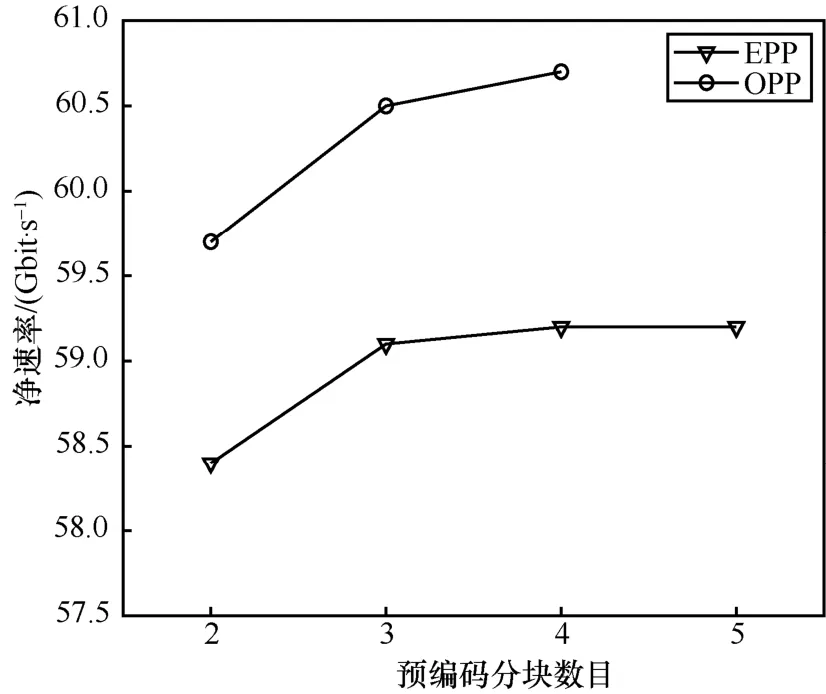
图15 EPP 与OPP 的净速率与预编码分块数目关系

综上所述，得益于PS-QAM 的整形增益与精细粒度的频谱效率调节能力，熵加载方案表现出远胜于使用普通QAM 的自适应加载方案的速率。但以子载波为粒度的熵加载方案复杂度极高，不适合实际使用。自适应预编码分块与熵加载结合将以子载波为粒度的加载更改为以预编码块为粒度的加载，有效减少了使用的PS-QAM 数目。并且本节所提OPP 方案可针对信道特性选择最优的预编码分块组合。实验表明，对于EPP 与OPP 这2种分块熵加载算法，3个预编码块（3种PS-QAM）已足够实现较好的性能，相比于EPP 与LC，OPP 表现出最优的速率。在净速率为60 Gbit/s 且传输距离为80 km 时，OPP 相比于LC 算法提高了4.4 dB 的接收机灵敏度。

图16 LC、EPP 与OPP 的净速率与接收光功率关系

5 结束语

本文以DMT 传输方案为基础，通过调制编码技术实现了3种高性能的自适应传输方案：调制、功率与FEC 三维自适应调制编码、自适应分块预编码与自适应分块熵加载。第一种方案针对传统QAM 调制格式的粗粒度问题，引入不同码率的FEC 改善调制粒度，提高编码增益，且基于查找表，相比于传统基于迭代的比特与功率二维加载算法大幅降低了算法复杂度。第二种方案解决DMT 系统高PAPR 与预编码方案速率受限的问题。通过灵活分块预编码，提出的算法达到传统自适应算法的速率，并最高可降低2 dB 的PAPR。第三种方案采用PS 技术提高QAM 调制格式的整形增益，显著改善了调制粒度，但也增加了调制复杂度。所提分块熵加载算法依靠信道特性与预编码SNR 均衡原理，对子载波分块加载PS-QAM，显著减少使用的PS-QAM 种类，并实现远胜于传统自适应算法的速率。这3种方案从调制编码的角度改善传输性能，在优化角度与算法复杂度上有所差异。在应用角度，可针对具体场景取舍调制编码方式，在性能、复杂度和成本等因素间寻找最佳的权衡点。在中短距传输系统中，自适应调制编码可在不明显修改硬件的条件下有效提高传输质量，针对特定信道或业务需求敏捷调整，有效支持未来灵活大容量光网络的建立与发展。