SIMON 轻量级密码算法的唯密文故障分析
李玮 ,吴益鑫,谷大武,李嘉耀,曹珊,汪梦林,蔡天培,丁祥武,刘志强
(1.东华大学计算机科学与技术学院,上海 201620;2.上海交通大学计算机科学与工程系,上海 200240;3.上海市可扩展计算与系统重点实验室,上海 200240;4.上海市信息安全综合管理技术研究重点实验室,上海 200240)
1 引言
随着信息技术与计算机技术的高速发展,物联网正逐步深入人们生活中,如何保障其中的信息安全问题已成为行业关注的焦点[1-2]。由于物联网环境中的传感器设备和射频识别技术等计算能力弱,存储量少,无法承载传统的密码算法,这就要求设计出执行效率高且吞吐量低的轻量级密码算法。轻量级密码算法由于其自身优势得到广泛应用,作为实现保密、完整性保护及认证的核心体制,其设计、分析和实现方法成为密码学研究的主流[3-5]。研究学者相继提出了多种轻量级密码算法,适用于物联网环境中类似RFID(radio frequency identification)、智能卡和密码芯片等计算能力有限的微型计算设备[6-7]。
轻量级密码算法在快速发展的同时,其安全性分析也受到人们的广泛关注。例如,传统密码分析方法中的线性攻击、差分攻击、不可能差分攻击、立方攻击和差分-线性攻击等[8-10]。然而,在物联网环境中,单纯从密码算法的设计结构上研究安全性已经远远不够,攻击者可以借助激光照射、异常时钟和涡流磁场等方式干扰加密实现过程使其出错,从而泄露一些中间状态信息,利用中间状态信息获取密钥,这种攻击被称为“故障分析”[11-15]。由于其高效的攻击效果和潜在的威胁性,故障分析已成为国内外密码学领域的主流研究方向之一。
故障分析在发展过程中,逐步出现了多种类型的分析方法。1997年,Biham 等[16]提出了一种新型的故障分析——差分故障攻击(DFA,differential fault attack),它是目前应用范围较广的一种故障分析技术。之后,又出现了不可能故障分析[17]、线性故障攻击[18]、中间相遇故障分析[19]、代数故障攻击[20]、无效故障分析[21]、碰撞故障分析[22]和唯密文故障分析[23]等攻击方法。上述方法均属于选择明文攻击(CPA,chosen plaintext attack)。然而,选择明文攻击有一定局限性,攻击者需要明确地知道明文以及对应的正确密文与错误密文,从而得到正确的密钥。
在故障分析中,唯密文故障攻击(CFA,ciphertext-only fault attack)是目前唯一一种能够在唯密文攻击(COA,ciphertext-only attack)的假设下进行攻击的技术[24]。攻击者在仅得到错误密文的情况下对密码算法进行破译,通过在加密过程的特定轮数导入随机故障,获得错误密文,解密密文获得中间状态,利用统计学的原理分析中间状态的分布律,即可获得正确密钥。由于唯密文攻击对攻击者能力要求最低,因此一旦攻击成功,会对密码算法的安全性造成巨大威胁。目前,在国内外的研究中,唯密文故障攻击Feistel 结构的密码算法仅有LBlock 轻量级密码算法,因此本文针对Feistel 结构的SIMON 密码算法进行唯密文故障攻击[25]。
2 相关工作
1997年,Boneh 等利用随机故障成功破译了RSA算法,此后,故障分析在评测新型密码体制安全的方法中占据了重要的位置。SIMON 密码是美国国家安全局在2013年所提出的一种Feistel 结构的轻量级密码算法[26]。SIMON 密码被设计出后受到了人们的广泛关注,研究者对该算法进行了大量的故障分析研究。2014年,Tupsamudre 等[27]首次对SIMON 密码进行差分故障分析,通过单比特故障模型和单字节故障模型在倒数第二轮导入故障。其中,若要恢复最后一轮密钥的16 bit,则需要8个单比特故障或者2个单字节故障。为了进一步减少导入故障数,2015年,Takahashi 等[28]针对SIMON 密码进行了差分故障攻击,在随机“与”故障模型下,在SIMON128/128版本中,通过在倒数第二轮导入7.8个故障数成功恢复出整个密钥,这是首次通过随机故障模型成功恢复整个密钥。2016年,Chen 等[29]提出了改进的差分故障攻击,在字节故障模型下使用最多6.0个故障数就能破译出密钥,成功减少了所需故障数。除了差分故障分析外,2017年,Ma 等[30]对SIMON32/64版本与SIMON128/128版本进行代数故障攻击(AFA,algebraic fault attack)。结果表明,在SIMON 32/64版本中,通过单比特故障模型将故障导入第26轮,只需5.0个故障数就能恢复整个密钥;在SIMON128/128版本中,将故障导入第65轮,只需2个故障数即可求得密钥。上述分析方式都是选择明文攻击,本文对SIMON 密码进行的唯密文故障分析研究是一种在唯密文攻击假设下进行攻击的密码分析技术。表1列出了目前针对SIMON 密码的故障分析研究,分别是差分故障攻击和代数故障攻击,这2种分析方法都属于选择明文攻击,本文针对SIMON 密码提出了唯密文故障攻击,该分析方法属于唯密文攻击。
唯密文故障攻击是Fuhr 等[24]于2013年针对SPN 结构的AES(advanced encryption standard)密码算法提出的一种新型故障攻击,通过在算法加密过程中导入随机故障,获得大量错误密文样本,统计某一轮中的中间状态值,利用统计学中的理论恢复出密钥。其中,在字节故障模型下,通过在倒数第二轮导入80个故障数,利用SEI(square Euclidean imbalance)区分器恢复出密钥;通过在倒数第一轮导入56个故障数,利用MLE(maximum likelihood estimate)区分器恢复出正确密钥。李玮等[31]于2017年针对代换置换结构的LED 轻量级密码算法改进了唯密文故障攻击,除了原有的区分器外,又提出了2种效率更高的新型区分器,分别是拟合优度GF(goodness of fit)区分器和GF-SEI 双重区分器。2018年,李玮等[25]提出了针对Feistel 结构的LBlock轻量级密码算法的唯密文故障攻击,同时提出了2种新型双重区分器GF-MLE 和MLE-SEI,减少了导入故障数,提高了攻击效率。
本文提出了SIMON 密码的新型唯密文故障攻击,将故障导入在倒数第三轮,在已有的区分器SEI、GF、MLE、MLE-SEI、GF-SEI 和GF-MLE的基础上,提出了新型的双重区分器GF-MAP、HW-MLE、GF-HW 和HW-MAP。表2总结了AES密码、LBlock 密码和SIMON 密码中所使用的区分器。在AES 密码中,仅使用了2种区分器对其进行破译;在LBlock 密码中,使用了6种区分器;在SIMON 密码中,除了原先的6种区分器,又使用新提出的4种新型区分器对密码进行破译。表3列出了针对各个版本SIMON 密码的唯密文故障分析部分子密钥结果对比,展示了使用不同的区分器破译各个SIMON 密码所需要的故障数。
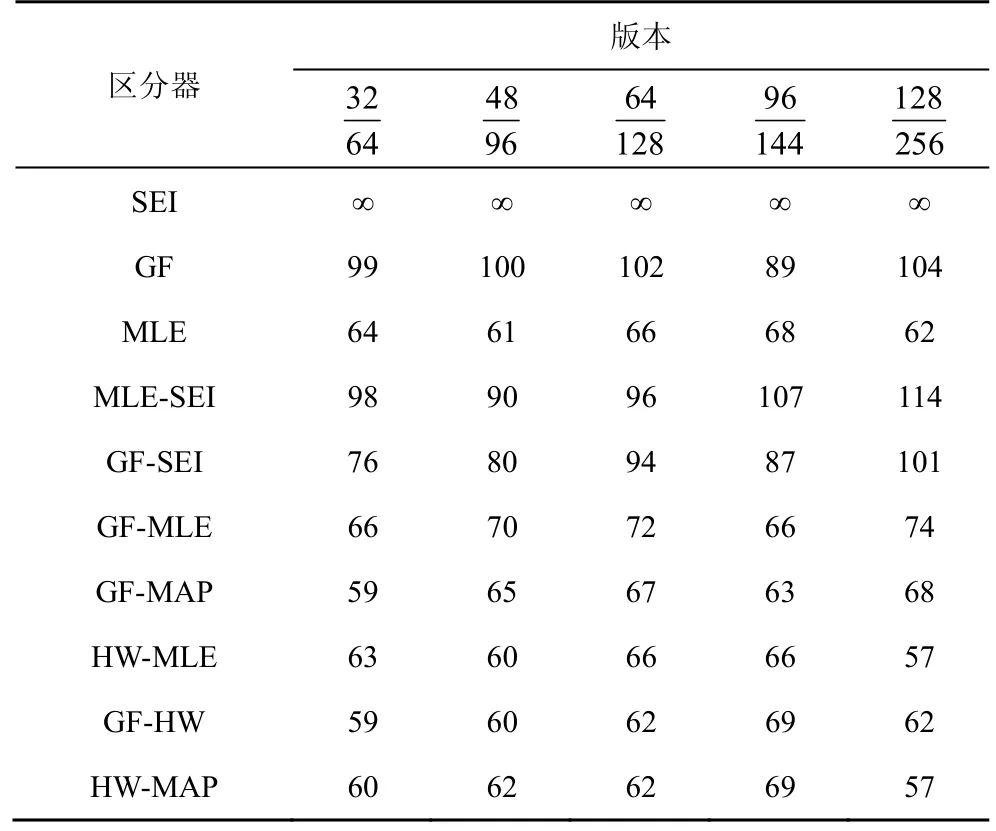
表3 SIMON 密码各版本的唯密文故障分析部分子密钥结果对比
3 SIMON 密码简介
3.1 符号说明
记M=X1||X0为明文。其中,将明文分成左右2个分支,C=XT+1||XT为密文,为错误密文,T为算法轮数;K为密码算法的主密钥,ki为轮密钥,每个轮密钥由主密钥通过密钥编排算法生成,其中i∈[0,T-1];St表示向左移t位,S-t表示向右移t位。
3.2 SIMON 密码算法
SIMON 密码是一种典型的Feistel 结构的迭代型分组密码。SIMON 密码的分组长度为2n,密钥长度为mn,其中,n∈{16,24,32,48,64},m∈{2,3,4},本文中记算法版本名称为 SIMON2n/mn。以SIMON32/64版本为例,其明文长度为32 bit,密钥长度为64 bit。SIMON 密码的版本信息如表4所示。

表4 SIMON 密码各版本
在加密算法中将消息明文分成左右2个等长的分支进行左右交替变换。SIMON 密码主要由加密、解密与密钥编排3个部分组成。其中,解密过程是加密过程的逆运算。SIMON 密码的结构如图1所示。

图1 SIMON 密码的结构
第i轮的计算式为

其中,0≤i≤T-1。首先左分支左移1 bit 与左分支左移8 bit 进行与运算,然后与右分支进行异或运算,将得到的结果与左分支左移2 bit 进行异或,最后与该轮子密钥异或成为下一轮的左分支,下一轮的右分支即为上一轮的左分支。该运算方式迭代运行T轮。
3.3 密钥编排方案
主密钥K通过密钥编排方案产生每一轮的子密钥{k0,k1,k2,…,kT-1},在SIMON 密码中,每个版本的密钥编排方案根据密钥mn的值进行分类,密钥编排方案如下。
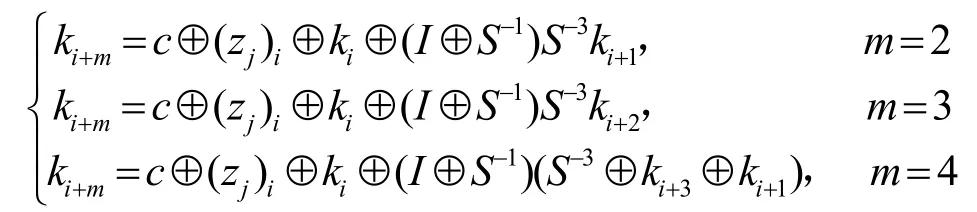
其中,c=2n-4,zj为固定常数序列值,I为原值。
4 唯密文故障分析
4.1 基本假设和故障模型
本文算法中,唯密文故障攻击的基本假设为攻击者对随机明文使用同一个密钥进行加密,并在加密过程的特定轮数导入随机故障,获得大量的错误密文样本。
本文针对 SIMON32/64、SIMON48/96、SIMON64/128、SIMON96/144和SIMON128/256这5个版本进行了攻击实验,采用的故障模型都是半字节随机故障模型,在加密过程中倒数第三轮的左分支导入故障,使其产生随机半字节故障值。
4.2 基本步骤
针对SIMON 密码的唯密文故障攻击过程可以分为以下几个步骤。
步骤1确定导入故障模型,保证明文随机产生,用同一个密钥对其进行加密。在加密过程中指定轮数导入随机故障,生成错误密文。
步骤2对密文进行解密,求出中间状态值受密钥与密文影响的关系,对中间状态值进行统计分析,通过区分器得到每个候选密钥值的区分器值,选择区分器最大值或最小值求出子密钥的部分比特位。
步骤3重复上述步骤,更换故障导入位置,求出子密钥其余部分的比特位,之后可以用密钥编排方案推出主密钥。
4.3 具体过程
本文提出了针对SIMON 轻量级密码算法的唯密文故障攻击,在已有的6种区分器的基础上,针对SIMON 密码提出了4种新型区分器,分别是GF-MAP 双重区分器、HW-MLE 双重区分器、GF-HW 双重区分器和HW-MAP 双重区分器。具体攻击过程如下。
步骤1选择一个密钥,用该密钥对随机明文进行加密,导入随机半字节故障,得到错误密文样本。以SIMON64/128版本为例,导入位置可以是图2中X42左分支上的任意半字节,若导入位置为第一个半字节,则扩散路径如图2所示。导入位置不同故障扩散的路径也不同。
步骤2穷举密钥候选值,推算出每个密钥候选值所对应的中间状态样本组,中间状态可以用密文与密钥来表示,计算式为
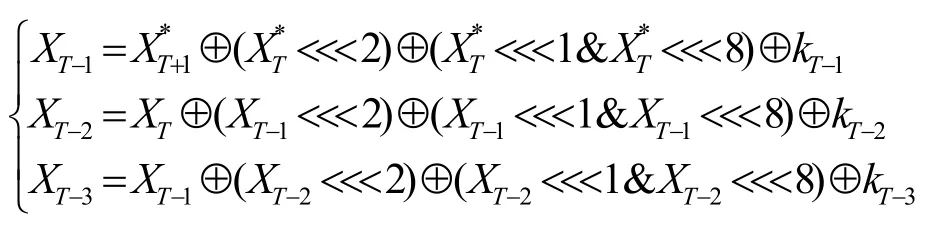
步骤3得到中间状态样本组之后,用区分器对中间状态进行统计分析。每个密钥候选值都对应导入故障数的错误密文,每个错误密文都可以根据密钥候选值求出一个中间状态值。因此,每个密钥候选值对应一组中间状态,每组样本值都可以用区分器计算出所对应的区分器值,选择不同的区分器进行统计分析,选取区分器最大值或最小值所对应的密钥候选值就是所求的正确子密钥。
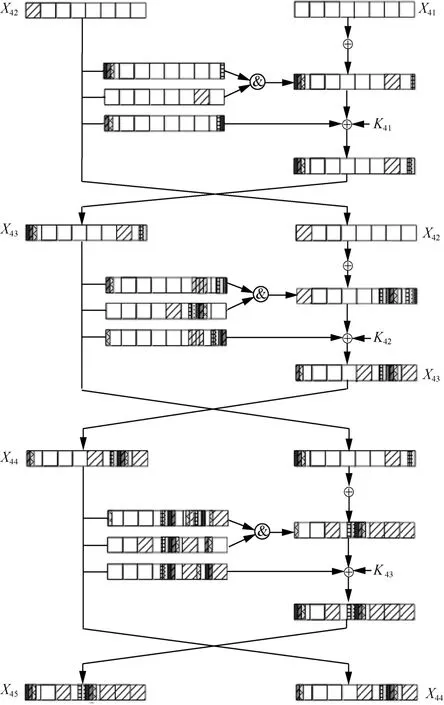
图2 SIMON64/128中故障导入在倒数第三轮的路径扩散
在SIMON32/64版本中,上述步骤可恢复出k31的半字节与k30的9 bit,重复上述步骤4次,即可恢复出k31的4个半字节和k30的4个半字节,之后,通过密钥编排方案求出主密钥。在其余4个版本中,由于密钥编排的特殊性,每次能获得2个密钥候选值,这2个密钥候选值中将会有11 bit 是相同的值且是正确值,将这2个候选值进行比较,选取比特位相同的数值,即为所求位置正确的值,每次可恢复出倒数第二轮子密钥的3 bit 和倒数第一轮中子密钥的8 bit。
4.3 区分器
本文对SIMON 密码进行唯密文攻击过程中所使用到的区分器一共有10种。本节先介绍已有的6种区分器,再介绍本文提出的4种新型双重区分器,分别是GF-MAP、HW-MLE、GF-HW 和HW-MAP。
4.3.1 SEI 区分器
平方欧氏距离(SEI,square Euclidean imbalance)区分器主要用于统计未知分布与均匀分布之间的距离,求出最不满足均匀分布的样本即为所求正确密钥对应样本组。计算式为
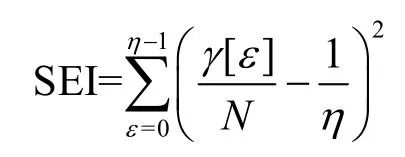
其中,η=24,由于本文使用的是随机半字节故障,因此η表示半个字节所有排列组合个数;ε∈[0,15];N为导入故障数;γ[ε]统计中间状态为ε时的个数。针对每个密钥候选值都有对应的样本组,样本容量为N,求出每个样本组所对应的SEI值,越不符合均匀分布所得SEI 值越大,该样本所对应的密钥候选值即为正确子密钥。
4.3.2 GF 区分器
拟合优度(GF,goodness of fit)区分器在使用时要求先求出理论分布律。通过比较实际求得的分布律与理论分布律之间的差值,差值最小时,说明该样本是所求样本。图3为本文中间状态的理论分布律。区分器计算式为

其中,η表示半个字节所有排列组合个数,Oε表示在密钥候选值对应样本里中间状态值为ε时的实际个数,ϒε表示同等样本量条件下中间状态值为ε时的理论个数。通过比较对应中间状态值相同时实际与理论个数之差,判断出最接近理论分布的样本。GF 值越小,越接近理论分布。

图3 半字节故障按位与导入后的分布律
4.3.3 MLE 区分器
极大似然估计(MLE,maximum likelihood estimate)区分器是Fuhr 等针对AES 密码算法提出的一种区分器。区分器计算式为

其中,M为导入故障数,m∈[0,M-1],ΨT-3表示倒数第三轮的中间状态值。将样本中所有的中间状态值的理论概率相乘,求出每个密钥候选值对应的极大似然估计值,其值越大,越满足概率分布,从而可以求得对应正确子密钥。
4.3.4 MLE-SEI 区分器
将MLE 区分器与SEI 区分器相结合,构建双重区分器,首先用极大似然估计求出部分密钥候选值集合,将其记为χ(k),再用SEI 区分器在剩下密钥中选出最优解。计算式为
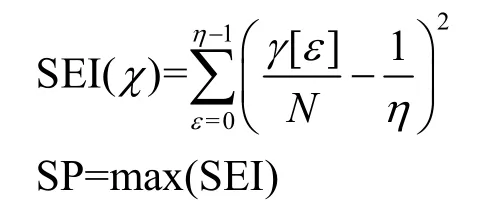
针对χ(k)集合中的每一个密钥候选值k求出对应的SEI 值,进行二次筛选,最后选择SEI 值最大的样本SP,该样本对应候选值即为正确子密钥。
4.3.5 GF-SEI 双重区分器
将GF 区分器与SEI 区分器结合,先用拟合优度筛选出接近理论分布样本χ(k),由于实际分布不可能与理论分布完全一致,因此设定一个临界值,通过自由度df 查找上侧位卡方分布表χ2中对应的临界值,规定当时,样本服从该已知分布,在本文中定义精度为0.05。再用SEI 区分器筛选出正确子密钥。
4.3.6 GF-MLE 双重区分器
GF-MLE 双重区分器先用拟合优度过滤不满足分布的密钥候选值,得到密钥集合χ(k),再使用MLE 区分器进行筛选。

求出剩下集合中每个密钥候选值对应的MLE值,选取MLE 值最大的样本组,即为正确样本。
4.3.7 GF-MAP 双重区分器
为了进一步减少故障数,本文将GF 区分器与参数估计之最大后验估计(MAP,maximum a posteriori)区分器相结合,提出了新型区分器GF-MAP双重区分器。实验证明,该区分器能有效减少导入故障数,在较短时间内实现算法破译。与前2种区分器相似,先用拟合优度选出接近理论分布律的密钥候选值集合χ(k),再用MAP 区分器进一步选出最优子密钥。
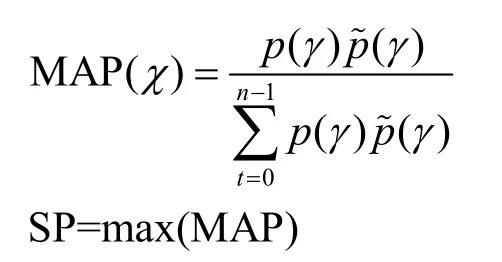
其中,p (γ)表示中间状态值为γ的概率,表示对应密钥候选值的先验概率,n表示密钥候选值的穷举范围。选取MAP 值最大的样本组SP,该样本所对应的密钥候选值为正确密钥。
4.3.8 HW-MLE 双重区分器
汉明重量(HW,hamming weight)可用于统计半字节或字节中非0的位数。该区分器可适用于更深的轮数中随机故障模型的统计。计算式为
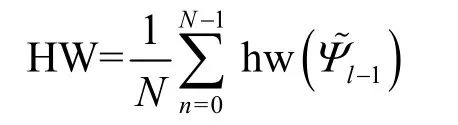
其中,N表示故障数,0≤n≤N-1,表示每一组错误的中间状态样本,hw 表示求出的中间状态样本所对应的汉明重量值。在随机半字节故障中,理论上得到的半字节中比特位为0的概率最大,所以HW 区分器中所求得的值越小,说明所得密钥越正确。本文结合HW 区分器与MLE 区分器构建了双重区分器。先用HW 区分器筛选,排除错误样本,剩下密钥候选值集合χ(k),再用MLE 区分器进行筛选。

针对集合χ(k)中的每个密钥候选值求出对应的MLE 值,选取值最大的MLE 值样本所对应的密钥候选值为所求正确子密钥。
4.3.9 GF-HW 双重区分器
为了进一步提高攻击效率,本文将GF 区分器与HW 区分器结合,先用GF 区分器筛选出符合分布的候选值集合χ(k),再将其用HW 区分器进行统计分析,筛选出最优密钥,计算式为
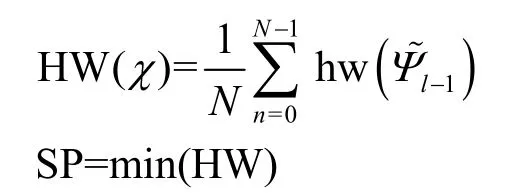
取HW 最小值的样本SP,找出该样本对应的密钥候选值就是最后所求的正确子密钥。
4.3.10 HW-MAP 双重区分器
本文还提出了HW-MAP 双重区分器,先用HW区分器进行筛选,求出候选值集合χ(k),再用MAP区分器进一步筛选出最优密钥,计算式为
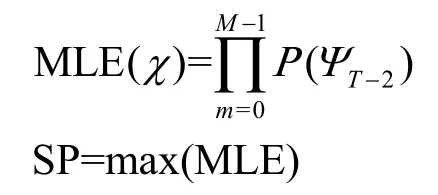
求出χ(k)集合中的每个密钥候选值对应的MLE 值,选取值最大的MLE 值样本对应候选值即为所求正确子密钥。
5 实验分析
本文实验在PC端(CPU为Inter Core I7-9700K,4.9 GHz,内存为16GB)使用Java 编程语言对SIMON 密码进行模拟唯密文故障攻击。在攻击过程中,模拟实现导入故障操作,之后对算法进行唯密文故障分析,用区分器恢复出主密钥。本文经过1000次实验操作,以99%的成功概率分别破译了SIMON32/64、SIMON48/96、SIMON64/128、SIMON96/144和SIMON128/256共5个版本的SIMON 密码,成功恢复出倒数第一轮与倒数第二轮子密钥。在实验过程中,分别记录了针对5种版本SIMON 密码的唯密文故障攻击过程中使用不同的区分器所需故障数、成功恢复密钥概率和耗费时间。
图4展示了SIMON 密码中5个典型版本恢复子密钥所需故障数对应的成功恢复密钥概率。图4中10种不同线型表示不同的区分器,分别为区分器SEI、GF、MLE、MLE-SEI、GF-SEI、GF-MLE、GF-MAP、HW-MLE、GF-HW 和HW-MAP,可以看出,各版本成功恢复密钥需要的最少故障数分别为59、60、62、63和57;SEI区分器的攻击成功概率最高仅达到83%,其他区分器均达到99%以上。
图5为SIMON 密码中故障数对应的消耗时间。图5中分别展示了SEI、GF 和MLE 单区分器,MLE-SEI、GF-SEI、GF-MLE、GF-MAP、HW-MLE、GF-HW 和HW-MAP 双重区分器所需消耗时间,可以看出,各版本成功恢复密钥需要的最少消耗时间为2.2 s、13.0 s、24.3 s、36.3 s 和41.2 s;SEI 区分器的攻击成功概率达到最高时消耗时间需要12.8 s。
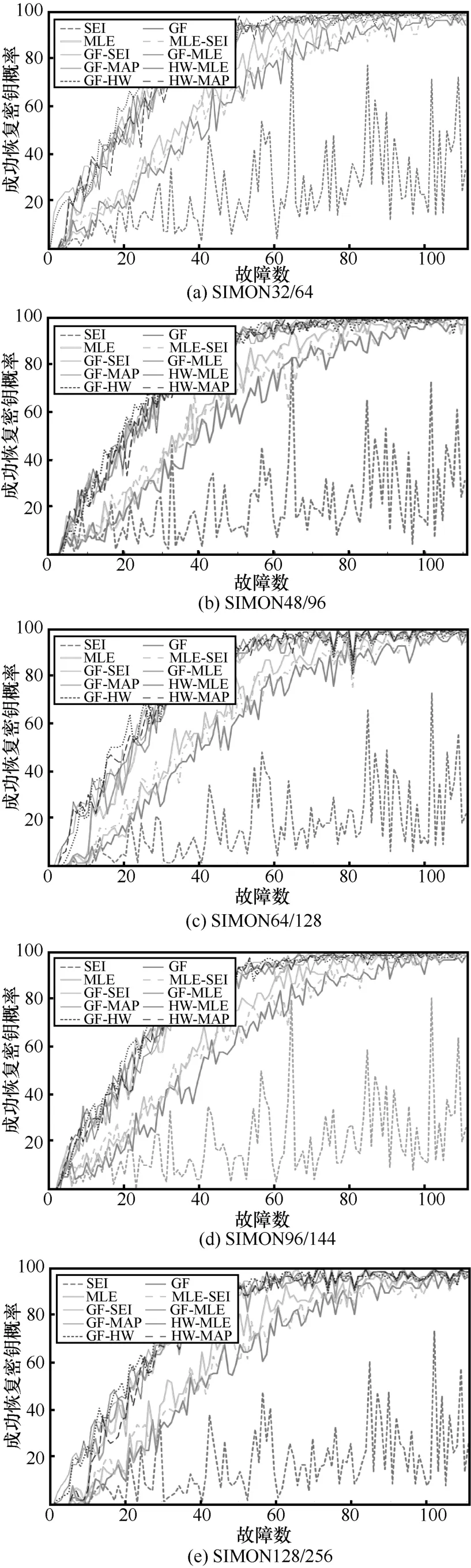
图4 各版本中故障数对应成功恢复密钥概率

图5 各版本中故障数对应的消耗时间
由图4和图5可知,随机“与”故障导入之后,受分布律以及数据量的影响,每个区分器都呈现各自的统计效率。按照攻击效果分类,10种区分器可以分成以下3组:SEI 区分器的攻击效率最低,在SIMON 密码中基本无效;其次是GF-SEI 双重区分器、MLE-SEI 双重区分器和GF 区分器,这3种区分器攻击效果并不显著;攻击效率明显较好的是 MLE 区分器、GF-MLE 双重区分器、GF-MAP 双重区分器、HW-MLE 双重区分器、GF-HW 双重区分器和HW-MAP 双重区分器。在SIMON32/64版本中,GF-MAP 双重区分器和GF-HW 双重区分器攻击效果最好,所需故障数最少且消耗时间最短,是该版本中最好的区分器。在SIMON48/96版本中,HW-MLE 双重区分器与HW-MAP 双重区分器所需故障数最少。在SIMON64/128版本中,GF-HW 双重区分器和HW-MAP 双重区分器所需故障数最少,双重区分器结合了单区分器的优点,在短时间内就能以99%的概率恢复出密钥。在SIMON96/144版本中GF-MAP 双重区分器所需故障数最少。在SIMON128/256版本中HW-MLE 双重区分器和HW-MAP 双重区分器仅需要57个故障数就能恢复正确密钥,HW-MLE 区分器所需时间最短,是该版本中最优区分器。
6 结束语
本文提出了针对Feistel 结构的SIMON 密码的新型唯密文故障分析。实验结果表明,在随机半字节故障模型下,本文新提出的4种新型区分器比已有的6种区分器所需故障数更少,在同等故障数的情况下,成功恢复出密钥的概率更高。由此证明,Feistel 结构的SIMOM 密码并不能抵抗唯密文故障攻击,这为其他类似结构的密码算法提供了借鉴,并为抵御唯密文故障攻击研究提供了重要的参考价值。
附录A 实验数据及结果
明文随机生成
密钥SIMON32/64版本主密钥为0123456789ABCDE F,SIMON48/96版本主密钥为0123456789ABCD EF01234567,SIMON64/128版本主密钥为0123456789 ABCD EF0123456789AB CDEF,SIMON96/144版本主密钥为0123456789ABCD EF0123456789 ABCDEF0123,SIMON128/256版本主密钥为0123456789ABCDEF0123456789ABCDEF0123456789ABC DEF 01234,56789ABCDEF。
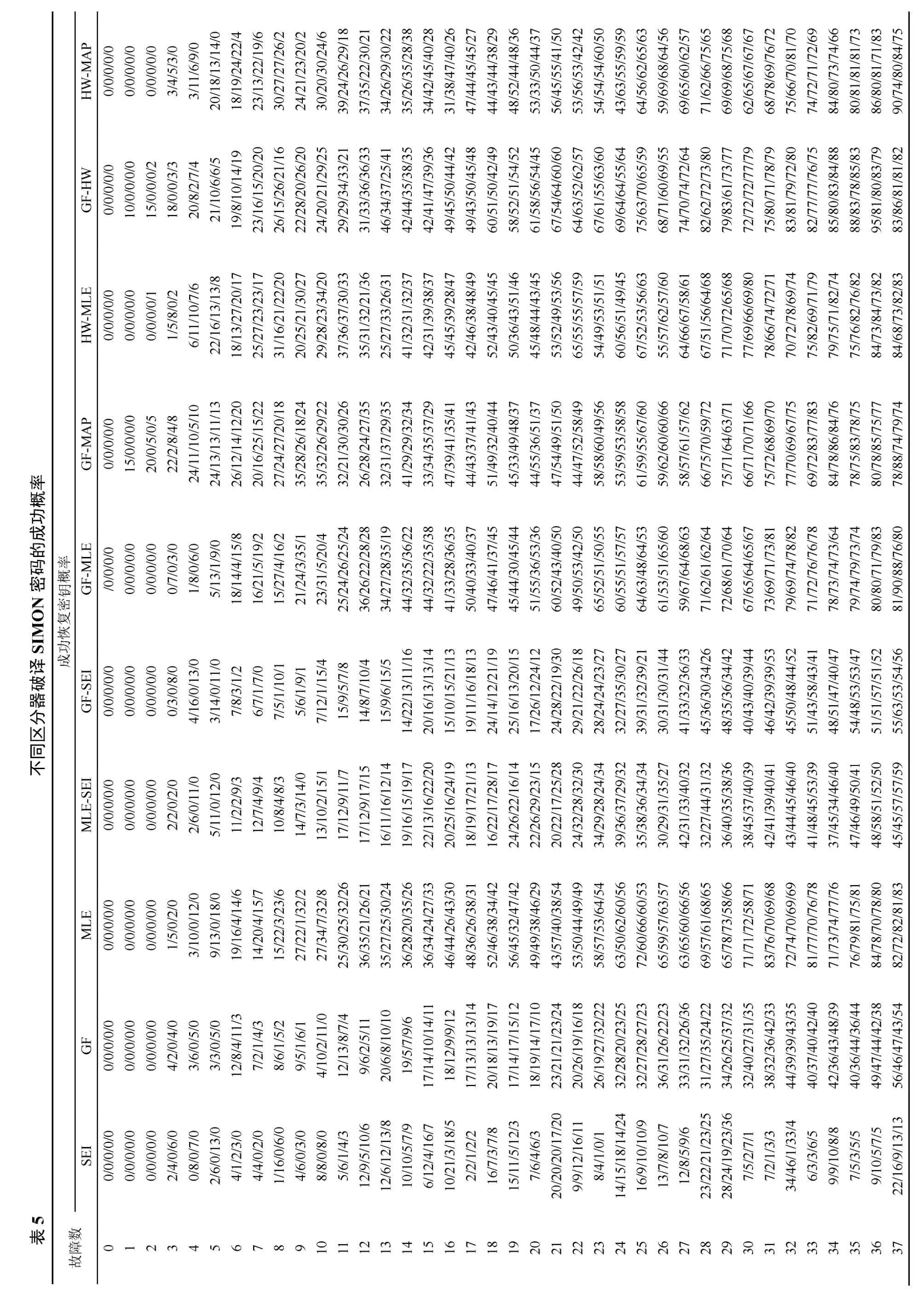
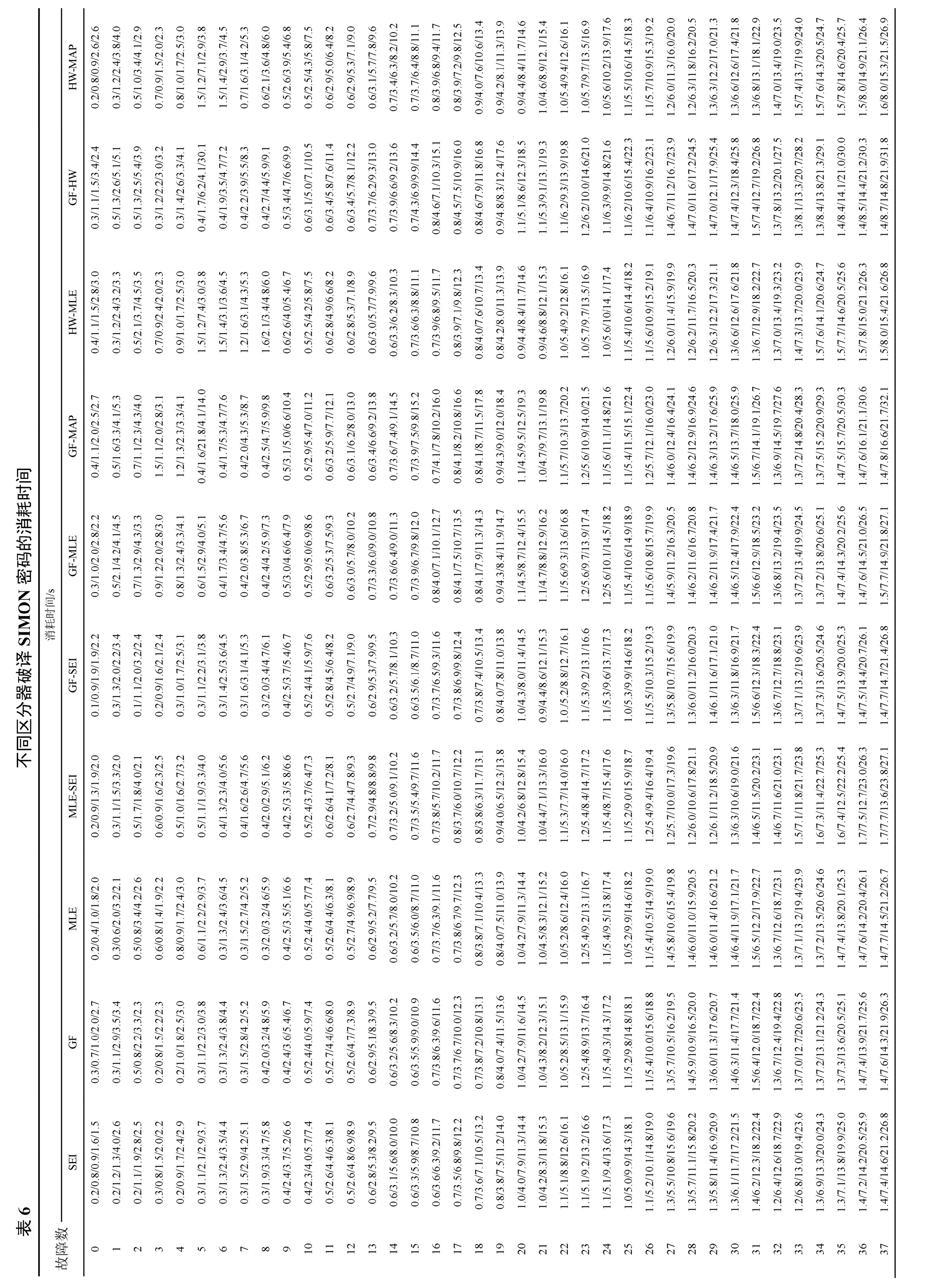
实验结果10种区分器均能恢复主密钥,实验数据分别如表5和表6所示。