基于渐近线选择的TDOA定位算法

胡 荣，李 琴

(1.文华学院城市建设工程学部，武汉 430074；2.辽宁省交通高等专科学校，沈阳 110122)

随着无线通信技术的快速发展以及人们对地理位置信息需求的增加，基于到达时间差(Time Difference of Arrival，TDOA)的无线定位技术在军事应用、空间探索、交通管理、紧急救援等领域应用越来越广泛[1-2]。TDOA定位算法不需要定位基站间保持时间同步，而且其抗干扰能力强、定位精度相对较高、隐蔽性好，在目前蜂窝系统移动台定位中占据重要位置[3-5]。

目前，常用的TDOA 定位算法主要包括Chan算法[6]、Taylor级数算法[7]、Fang算法[8]等。Chan算法的优势在于当测距误差较小时，定位精度较好，但当测距误差增大时，定位精度会迅速降低；Taylor级数算法由于采用迭代运算，定位精度受迭代的初始选择点影响较大；Fang算法同样在测距误差较大时性能会降低很多。近年来，许多基于TDOA的改进定位算法被提出。文献[9]在常用的Chan算法中融入差分演进算法，减小了测量噪声对定位精度的影响；文献[10]将加权最小二乘法应用在TDOA定位中，并利用阈值将坐标参数和测量值分开，建立待求基站的线性方程；文献[11]针对Taylor级数算法中可能选择的较差初始值，使用衰减奇异值分解法进行修正，使迭代算法的求解结果能够收敛到真实位置，在低信噪比的情况下能有更好的定位精度。文献[12]建立了一种基于贝叶斯框架检测概率模型，通过该模型将TOA和TDOA测量值进行融合，实现目标定位。本文提出一种基于渐近线选择的TDOA定位算法，通过计算离心率选择合适的渐近线参与定位，提高了定位精度。

1 TODA双曲线定位模型

1.1 基本原理

TDOA双曲线定位[13]是通过测量无线信号从移动台到两个不同基站所需的时间差，计算移动台的坐标。如图1所示，利用测量得到的时间差，计算移动台MS到两个基站BS1，BS2的距离差，根据几何知识，MS位于以BS1和BS2为焦点的双曲线上。如果要得到MS的位置，还要求出MS到BS1和BS3的距离差，构建以BS1和BS3为焦点的双曲线，则两条双曲线交于两点，根据先验知识，可以确定MS的位置。

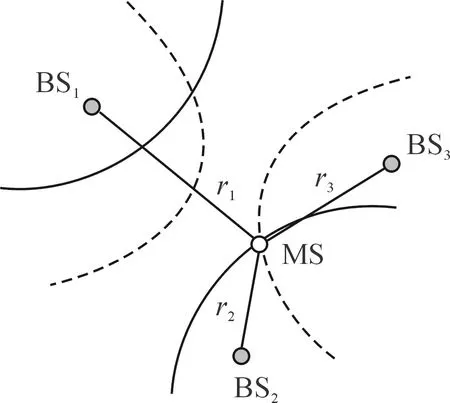
图1 双曲线定位示意图

1.2 定位模型

假设二维平面上有N个基站，BSi和BSj分别表示第i个和第j个基站，则移动台MS到两个基站BSi和BSj的测量距离差等于传播速度乘以测量时间差，由此可得：

rij=cΔtij=ri-rj

(1)

式(1)中:ri表示MS与BSi之间的测量距离；rj表示MS与BSj之间的测量距离；rij表示BSi和BSj间的测量距离差；Δtij表示无线信号从MS分别到达BSi和BSj的时间差；c表示信号传播速度。

将MS的坐标记为(x,y)，基站BSi的坐标记为(xi,yi)，另外，把BS1看作服务基站，可得：

ri1=cΔti1=ri-r1

(2)

式(2)中：

(3)

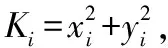
(4)

由式(4)可以得到一条双曲线，它的焦点坐标分别为(x1,y1)和(xi,yi)，并且MS处在该双曲线上。根据N个基站，可以得到N-1个Δti1测量值和N-1对双曲线。求解联立式(3)所示的N-1个等式，即可求出MS的定位坐标。

在式(3)中，令xi1=xi-x1，yi1=yi-y1，可得：

(5)

令：

则式(4)可表示为：

Ar=H

(6)

进而可以求出移动台MS的坐标。

2 基于双曲线渐近线的TDOA定位算法

在常用的TDOA算法中，Chan算法在噪声较小时才能取得较好的定位精度，Taylor级数算法的定位效果则受迭代初始值得影响，当初始值误差较大时，算法的收敛性会大大降低，影响定位效果。而以两个基站为焦点可以构成一对双曲线，本节利用此双曲线的渐近线构造方程组进行定位。

如图2所示，在XY坐标系中，基站BSi和BSj的坐标记为(xi,yi),(xj,yj)，以BSi和BSj为焦点形成一对双曲线，用Kij表示其渐近线的斜率，则该双曲线的渐进线为：

(7)

在图2中，α为BSi和BSj的连线和X轴形成的夹角，η表示BSi和BSj的连线和上述渐近线形成的夹角，则从图2可知，该渐近线和X轴间的夹角大小为α+η，并且：

(8)

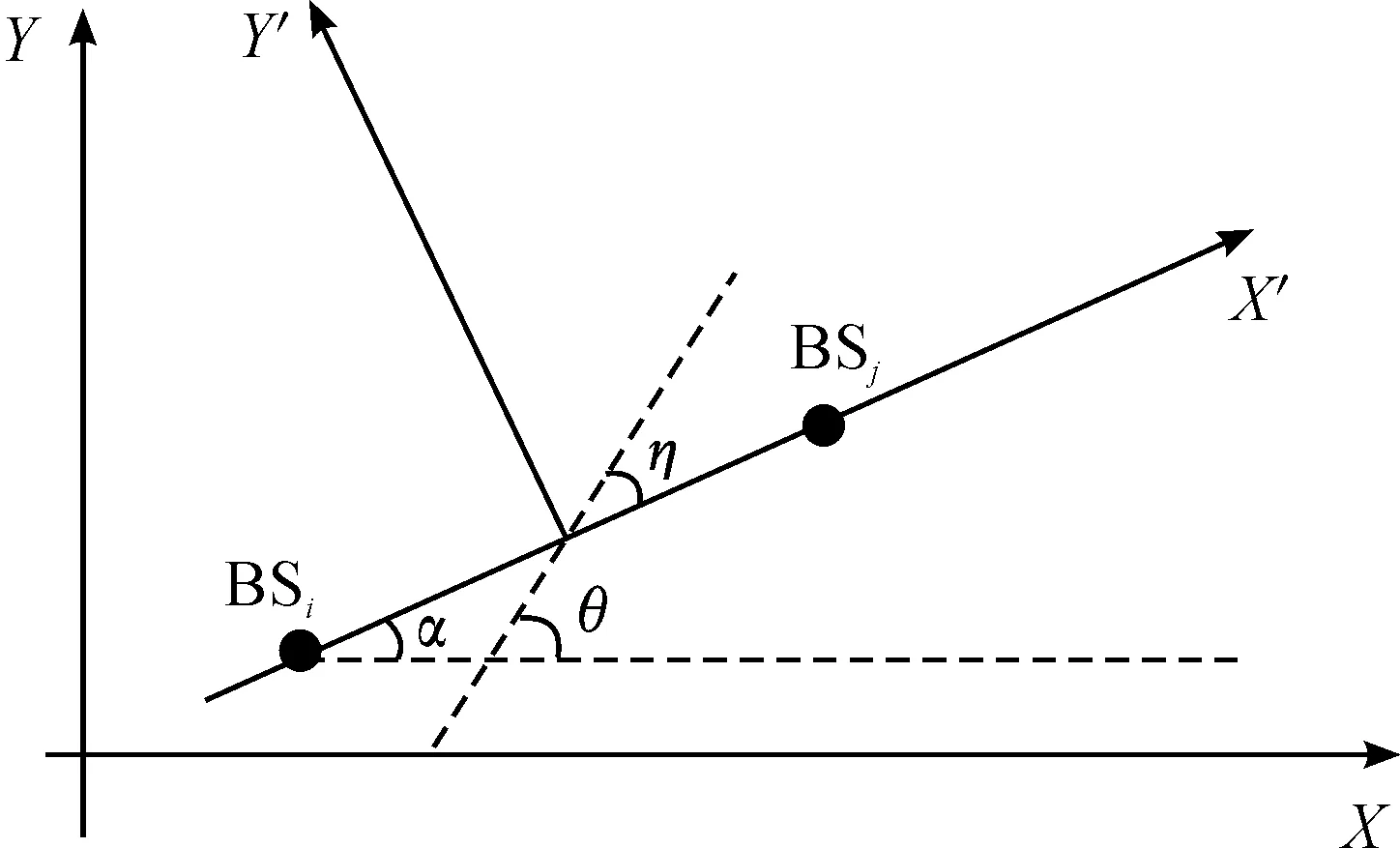
图2 渐近线斜率求解示意图

假设在图2所示的X′Y′坐标系下，BSi和BSj的坐标为(-c0,0)、(c0,0)，移动台MS的位置坐标记为(x′,y′)，MS到BSi和BSj的传输时间差TDOA值记为Δtij，信号传播速度记为c，则BSi和BSj间的距离表示为：

dij=2c0

(9)

可得到TDOA方程为：

(10)

则η可表示为：

(11)

以BSi和BSj为焦点确定的双曲线渐近线倾斜角表示为：

(12)

θij的正切值就是该双曲线渐近线的斜率，即：

Kij=tanθij

(13)

在XY坐标系下，MS的位置坐标记为(x,y)，N个基站的位置坐标记为BS1(x1,y1)，BS2(x2,y2)，…，BSN(xN,yN)。把基站BS1看作服务基站，可得双曲线的渐进线方程组为：

CX=D

(14)

式中：

在实际环境中，非视距等原因会导致出现误差，式(14)两端并不完全相等，式(14)可改写为：

CX-D=E

(15)

使用最小二乘法求解式(15)所示的超定方程组，可以得到较为精确的解，得：

f(X)=(CX-D)2=(CX-D)T(CX-D)

(16)

式(16)两端同时求导，并且令导数值为零，即：

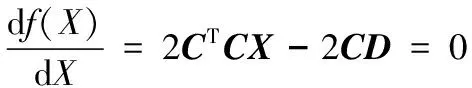
(17)

若CTC是非奇异矩阵，可求得X为：

X=(CTC)-1CTD

(18)

3 基于渐近线选择的TDOA定位算法

由式(12)、式(13)可以看出，渐近线的倾斜角与Δtij的值有关，应用在实际环境中时，TDOA估计存在误差，并且移动台MS和各个基站之间的测量距离差也存在误差εij，设实际测量得出的MS和各个基站之间的距离差表示为：

(19)

则渐近线的倾斜角测量结果表示为：

(20)

对式(20)右侧第二项进行泰勒级数展开，因为误差εij很小，这里仅展开到一阶导数部分，有：

(21)

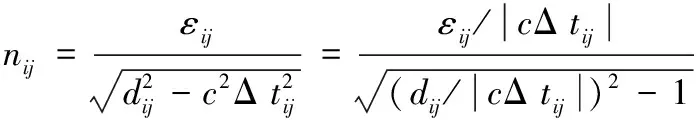
(22)

式(22)中，dij/|cΔtij|表示双曲线的离心率e，即e=dij/|cΔtij|。则式(22)可表示为：

(23)

如果噪声εij不变，离心率e会对nij的值产生重要影响。当e>1并且接近1时，e的微弱变化会引起nij的剧烈变化；当e<1时，计算结果为复数，此时应忽略该结果，重新选择基站进行位置计算。

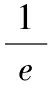
(24)

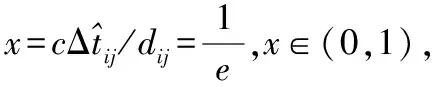
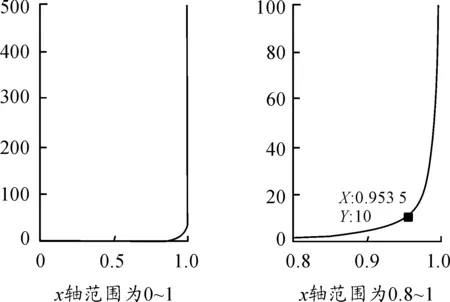
图3 f(x)=arccos x的弹性函数图像

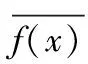
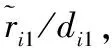
4 仿真分析

4.1 仿真条件

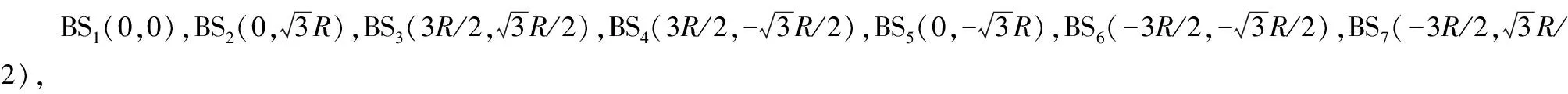
(25)

式(25)中，(X,Y)是MS位置的真实坐标值；(x,y)是MS位置的估计坐标值；n是仿真次数。

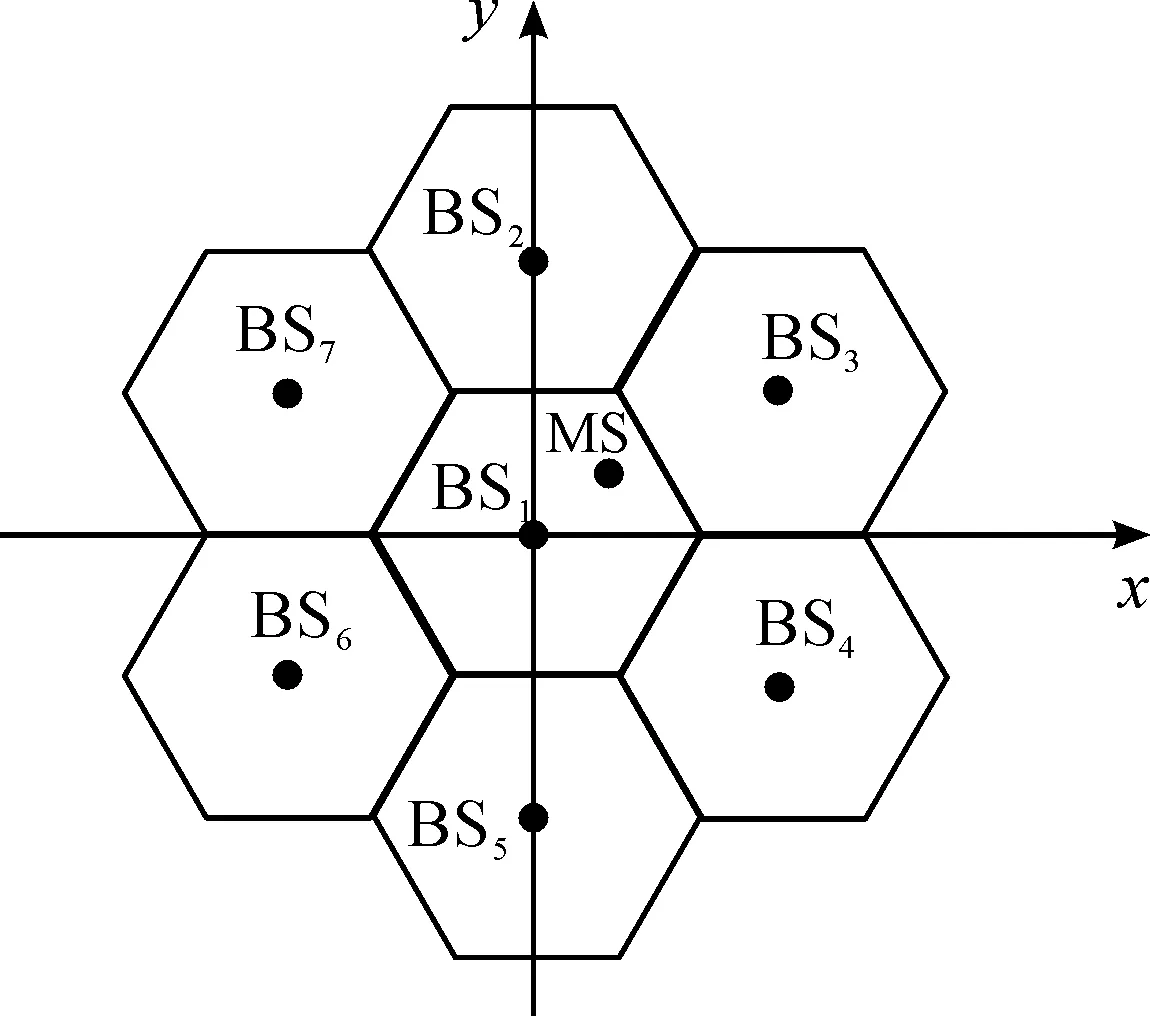
图4 小区内基站和移动台分布情况

4.2 仿真结果分析

1)小区半径和均方根误差的关系

图5所示为小区半径分别为2 km、3 km、4 km、5 km时，3种算法的定位性能比较，其中，TDOA测量误差的标准差取值为80 m，参与定位的基站数目为6个。由图5可知，当小区半径逐渐增大时，3种算法的均方根误差(RMSE)同样在增大。由于本文仿真只将测量误差考虑在内，忽略了非视距的影响，因此，Chan算法和Taylor算法能够将TDOA测量信息充分利用，当小区半径越来越大时，这两种算法的均方根误差曲线增加较为缓慢，本文算法的均方根误差曲线增加较快，但是本文算法的均方根误差始终小于其余两种算法。当小区半径为5 km时，本文算法的均方根误差分别相对于Chan算法和Taylor算法降低了9.7%和18.8%。

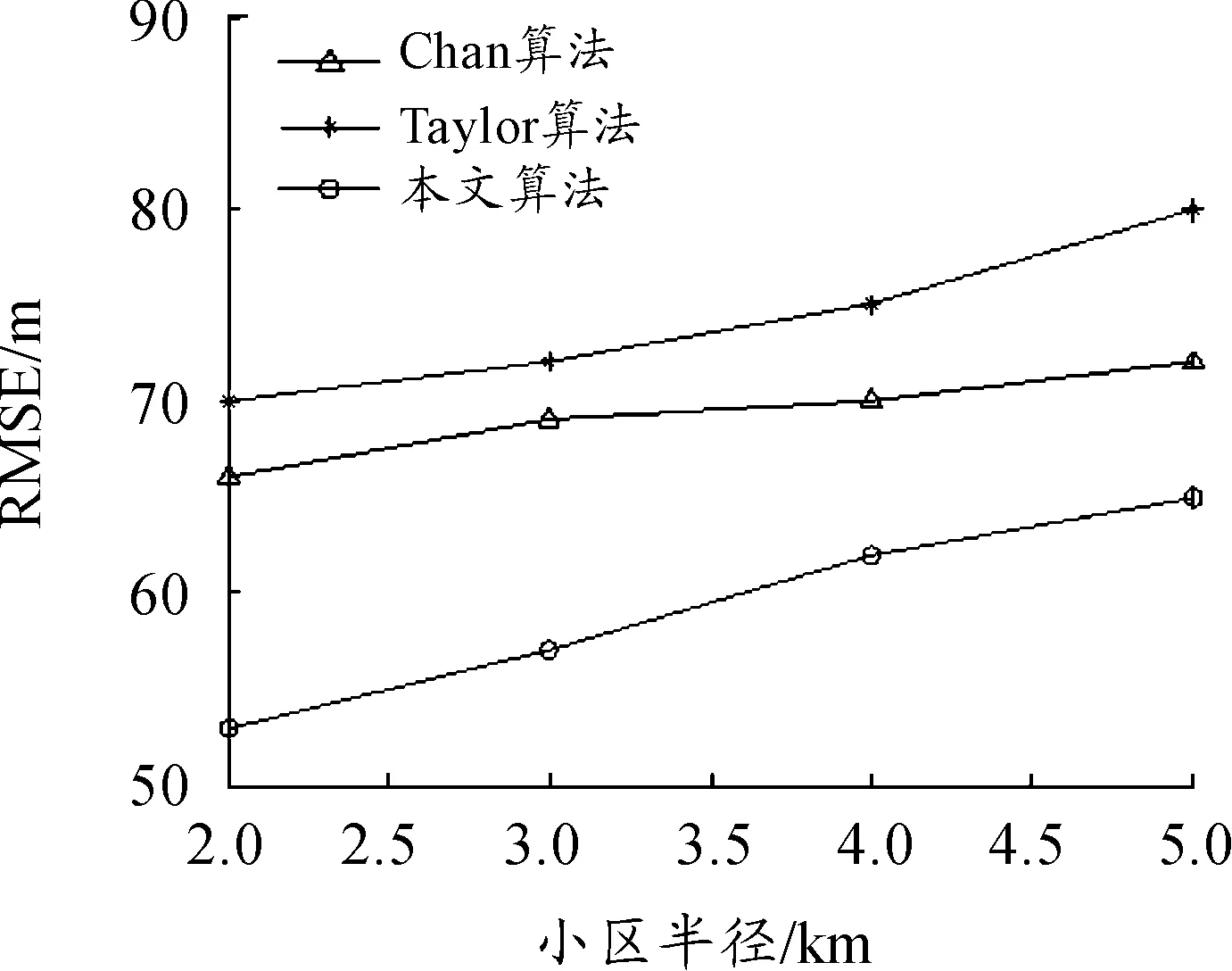
图5 小区半径和均方根误差的关系

2)基站个数和均方根误差的关系

图6所示为基站个数分别为4、5、6、7个时，3种算法的定位性能，其中，TDOA测量误差的标准差取值为80 m，小区半径为3 km。由图6可以看出，当参与定位的基站数目增加时，定位过程中产生的可用冗余信息就会更多，因此3种算法的定位精度也随之提高。同时，基站数目的增加也会使本文算法中双曲线的条数增加，在定位过程中选中的双曲线条数也会增加，本文算法的定位精度也就越高。当基站数目大于6个时，本文算法的均方根误差曲线逐渐趋于平稳，算法性能更加稳定。

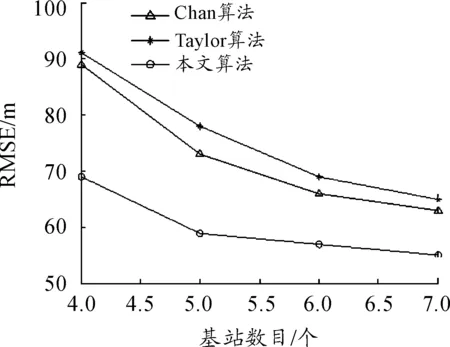
图6 基站个数和均方根误差的关系

3)测量误差和均方根误差的关系

图7所示为测量误差标准差分别为40 m、60 m、80 m、100 m、120 m时，3种算法的定位性能比较，其中，参与定位的基站数目为6个，小区半径为3 km。由图7可以看出，在测量误差较小的情况下，3种算法的均方根误差几乎相等。随着测量误差的增大，3种算法的均方根误差都在增大，但本文算法的定位性能相较于Chan算法和Taylor算法而言有明显的改善，这是因为本文算法在计算过程中对测量误差可能带来的影响进行了最大程度的规避，提高了定位性能。

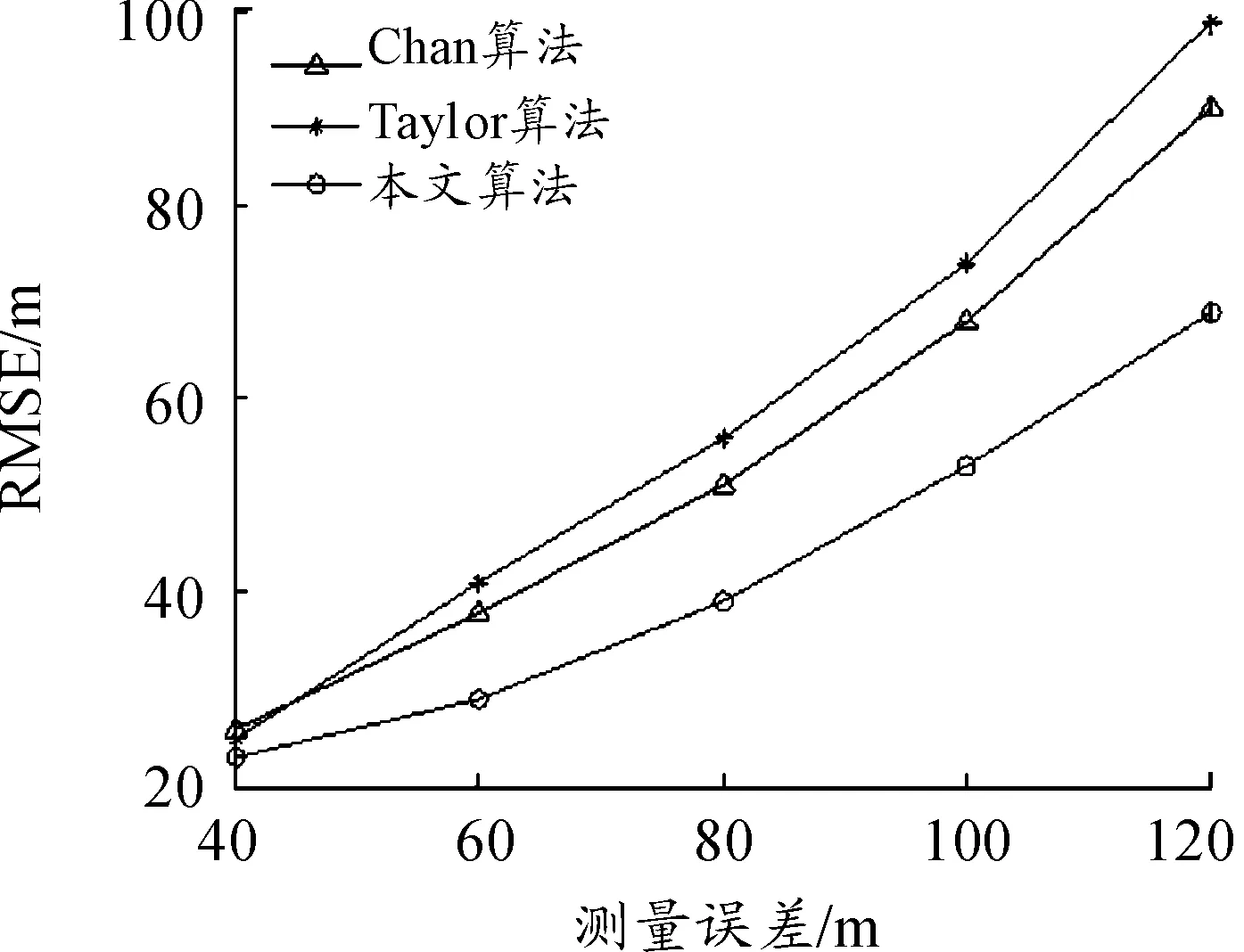
图7 测量误差和均方根误差的关系

5 结论

本文提出了一种基于渐近线选择的TDOA定位算法，在建立的基于双曲线渐近线的定位模型基础上，对双曲线渐近线的斜率表达式进行一阶泰勒级数展开，并分析了测距误差对定位结果的影响。然后根据引入的弹性函数设置阈值，根据离心率选择合适的渐近线进行位置估计，从而减小了离心率接近于1的渐近线对定位结果的影响。由仿真结果可知，相同条件下，可以获得比Chan算法和Taylor算法更好的定位效果。