三角阵列光电探测的双弹丸识别方法
高丰佳,董 涛,陈 丁,郑学明
(1.西安工业大学 陕西省光电测试与仪器技术重点实验室,西安 710021; 2.中国兵器工业集团有限公司 黑龙江北方工具有限公司,黑龙江 牡丹江 157000)
射击密集度是衡量身管武器系统性能的一项重要参数,其测试是兵器靶场试验的重要内容。目前,国内外已研究出了多种着靶坐标测量的方法,如多光幕交汇测量法[1-4]、双CCD交汇测量法[5-6]、声学原理方法[7-8]等。以上这些测量方法各有其优势,但当多弹丸着靶时,这些测量方法均存在一些缺陷,这可能导致弹丸测试过程中部分靶试数据丢失,或者理论上可行,但工程上实施难度较大,进而影响武器系统性能测试结果以及毁伤评估的科学性。
单管速射武器在有效射程内弹道可以视为直线[9],对其终点弹道进行损伤评估时,由于其射速较高,且各个弹丸飞行加速度存在一定的散布,可能存在后一发弹丸追上前一发弹丸的问题,即多弹丸同时着靶的现象。针对多弹丸同时过幕无法识别的问题,许多学者进行了研究,有研究人员提出在多光幕交汇测量法的基础上增加光幕数量实现多弹丸同时着靶的识别[10-12];在双CCD交汇测量法的基础上增加CCD相机数量解决该问题[13]。上述2种方法都虽能解决双弹丸同时着靶坐标测量问题,但均存在系统结构复杂、不便于装调、校准困难,难以实现工程化等问题。
相较于双弹丸同时着靶的概率,三弹丸及更多弹丸同时着靶的概率极低,可认为在有效射程内不会发生该事件[14],因此本项目只研究并解决如何识别双弹丸同时着靶的坐标测量。本研究从双弹丸同时着靶的问题入手,论述了三角光电探测阵列识别双弹丸的原理,并对其测量双弹丸着靶坐标原理进行建模分析,分析了其理论误差变化规律,并进行静态模拟实验。
1 双弹丸识别方法
1.1 工作原理
图1为所提出的三角阵列光电探测系统组成示意图。该装置主要由铝合金靶架、三个发光波段为780 nm的一字线激光器、等边三角形靶筐、宽度为2 mm的半导体光电探测器件、透过中心波长为780 nm的滤光片和信号处理装置等部分组成。将光电探测器件与滤光片整齐排列在三角形靶筐的三条边上构成三角形光电探测阵列,在三角形的三个角上分别安装一个激光器,光电探测阵列与激光器的出射光线共同构成测量幕面。当两发弹丸同时穿过测量幕面时,激光器投射在光电探测阵列上的部分光线被弹丸遮住,从而在光电探测阵列上留下弹丸投影,然后经信号处理得到弹丸投影的中心位置坐标。
图2为系统弹丸着靶坐标计算示意图,弹丸1与2同时穿过测量幕面,设其着弹着点为E1与E2,激光器1(其发光点为A)发出的部分光线被弹丸挡住,然后其所对应的三角形靶筐CB边的光电探测阵列上得到弹丸投影,通过信号处理装置对光电探测阵列进行处理即可得到激光器1对弹丸投影的中心A1,A2点;同理,对CA与AB边的光电探测阵列处理得到激光器2(其发光点为B)与激光器3(其发光点为C)对弹丸投影的中心B1,B2与C1,C2点。将激光器1的发光点A与它在对应边BC上对弹丸投影得到的中心点A1,A2分别相连;将激光器2的发光点B与它在对应边AC对弹丸投影得到的中心点B1,B2分别相连;将激光器3的发光点C与它在对应边AB对弹丸投影得到的中心点C1,C2分别相连。连接得到的六条直线,其中3条直线交于一点的点即为弹丸着弹点。如图2所示的直线A-A1、B-B1和C-C1的交点E1为弹丸1的着弹点,直线A-A2、B-B2和C-C2的交点E2为弹丸2的着弹点。

图1 系统组成示意图
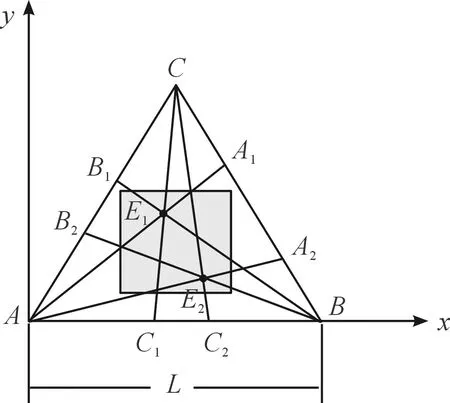
图2 系统弹丸着靶坐标计算示意图
1.2 测量模型
如图2所示,以激光器1发光点A所在点为原点建立直角坐标系,则A点的坐标为(0,0),设B与C所在点的坐标分别为(xB,yB)、(xC,yC),通过的双弹丸1与2的着弹坐标E1与E2分别为(xE1,yE1)、(xE2,yE2),光电探测阵列上弹丸投影的中心点A1的坐标为(xA1,yA1),A2的坐标为(xA2,yA2),B1的坐标为(xB1,yB1),B2的坐标为(xB2,yB2),C1的坐标为(xC1,yC1),C2的坐标为(xC2,yC2)。弹丸1着弹坐标E1可以由A-A1、B-B1、C-C1三条线中的任意两条解出;弹丸2的着弹坐标E2同理。
以A-A1与B-B1两条线来求解弹丸1着弹坐标E1为例:
直线A-C的斜截式方程为
(1)
直线B-C的斜截式方程为
即:
(2)
直线A-A1的斜截式方程为:
(3)
因为A1点在直线B-C上,则将坐标(xA1,yA1)代入式(2)得:
即:
yA1=K2(xA1-xC)+yC
(4)
将式(4)代入式(3)得:
(5)
直线B-B1的两点式方程为:
(xB1-xB)(yE1-yB)=(yB1-yB)(xE1-xB)
(6)
将式(5)代入式(6)得:
(yB1-yB)(xE1-xB)
(7)
因为点B1在直线A-C上,则将坐标(xB1,yB1)代入式(1)得:
yB1=K1xB1
(8)
将式(8)代入式(7)并化简得:
(9)
则弹丸E1的着弹点直角坐标为:
(10)
同样分析直线A-A2与B-B2的方程可以得到弹丸E2的着弹点直角坐标为:
(11)
以A-A1与C-C1两条线或者B-B1与C-C1两条线来求解弹丸1着弹坐标E1与以A-A1与B-B1两条线求解的结果时一致的,3种求解方法可以相互校准,这是本文交汇测量的优点之一。因3种求解方法分析过程一致,在此不再赘述。
2 理论误差分析
上文中用A-A1与B-B1这两条直线来求解弹丸1着弹点E1的坐标,因此,弹丸1着弹坐标E1与三个激光器发光点A、B、C和弹丸通过幕面时在光电探测阵列上的投影中心点A1、B1有关;则弹丸1着弹坐标E1的测量误差也与以上因素有关。由等边三角形靶筐的边长得到激光器发光点A、B、C的坐标,又由上文公式分析得到,A1点的y方向坐标与其自身x方向的坐标有函数关系,如式(4)所示;B1点的y方向坐标与其自身x方向的坐标有函数关系,如式(8)所示;则弹丸1着弹坐标E1的测量误差与A1点x方向的坐标和B1点x方向的坐标有关。以下为弹丸1着弹点E1的坐标测量误差的公式
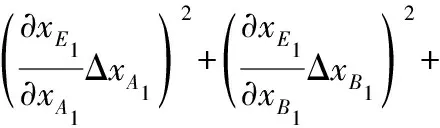
(12)
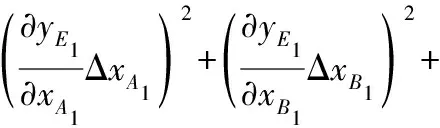
(13)
式中:ΔxE1和ΔyE1是弹丸1着弹坐标E1在x方向与y方向上的测量误差;∂xE1/∂xA1,∂yE1/∂xA1分别为xE1,yE1对点A1的x坐标求偏导所得到的误差传递系数;∂xE1/∂xB1,∂yE1/∂xB1分别为xE1,yE1对点B1的x坐标求偏导所得到的误差传递系数;∂xE1/∂xB,∂yE1/∂xB分别为xE1,yE1对点B的x坐标求偏导所得到的误差传递系数;∂xE1/∂yB,∂yE1/∂yB分别为xE1,yE1对点B的y坐标求偏导所得到的误差传递系数;∂xE1/∂xC,∂yE1/∂xC分别为xE1,yE1对点C的x坐标求偏导所得到的误差传递系数;∂xE1/∂yC,∂yE1/∂yC分别为xE1,yE1对点C的y坐标求偏导所得到的误差传递系数;ΔxA1是点A1的x坐标的测量误差;ΔxB1是点B1的x坐标的测量误差;ΔxB是点B的x坐标的测量误差即;ΔyB是点B的y坐标的测量误差;ΔxC是点C的x坐标的测量误差;ΔyC是点C的y坐标的测量误差。
由于各型弹丸口径不一,因此系统参数固定后对各型弹丸的分辨率也不尽相同。本文以口径为5.8 mm的弹丸进行分析,其余口径弹丸分析方法一致,且弹丸口径较大时为了防止弹丸击中靶筐,应相对应的增大系统参数。
在男人的指示下,楚墨进到一间茶室。茶室不大,装修尚好,墙上挂一幅《对弈图》,两个闲人坐在地上,半光着膀子,酒葫芦翻倒旁边。古琴曲《潇湘水云》飘起来了,小小的茶室里霎时云水掩映,烟波浩瀚。楚墨的心,也如同潮水般翻滚起来。
当L=5 m时,需要2 500×3个半导体器件。由于远离三角形靶筐处比靠近靶筐处的测量精度高,为了得到良好的测量精度,测量靶面取三角形靶筐中心的范围,大小为1 m×1 m。误差仿真条件为:
1)在x方向上可测量范围为0~5 m,则将x坐标的测量范围取为2~3 m;
2)在y方向上可测量范围为0~4.33 m,则y坐标的测量范围取为1.665~2.665 m;
3)发光点A点的坐标为(0,0),发光点B的坐标为(0,5 000),发光点C的坐标为(2 500,4 330);
4)取A1点的数据读取误差的x方向上的测量误差为ΔxA1=1 mm,取B1点的数据读取误差的x方向上的测量误差为ΔxB1=1 mm;
如图3与图4所示,为三角形光电探测阵列测量双弹丸坐标的误差仿真结果。
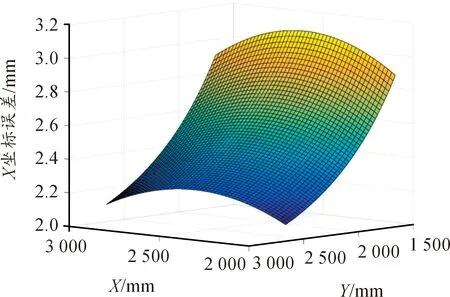
图3 x坐标测量误差分布
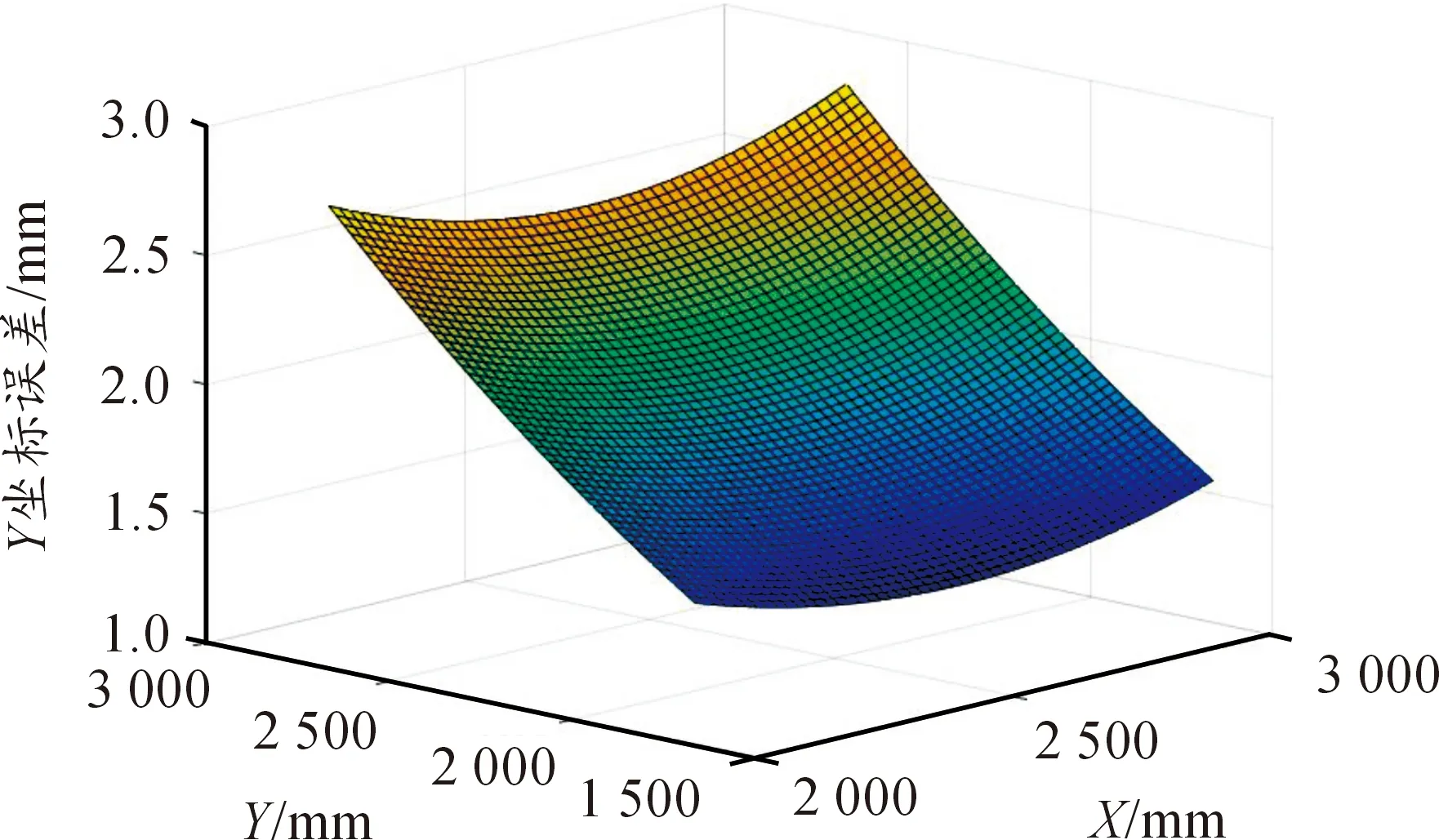
图4 y坐标测量误差分布
由图可以得到以下结论:
2)当y方向坐标不变,x方向坐标以x=2.5 m为轴向两边增加或减小时,x方向的测量误差缓慢减小,y方向的测量误差缓慢增加;
3)当x方向坐标不变,y方向的坐标由小变大时,x方向的测量误差显著减小,y方向的测量误差显著增大;
4)在x方向上的最大测量误差为3.107 mm,最小测量误差为2.101 mm,在y方向上的最大测量误差为2.789 mm,最小测量误差为1.378 mm。
则分析仿真结果可得:三角形阵列光电探测系统可以对双弹丸同时着靶情况下的坐标进行测量,在x方向上的测量误差为2.101~3.107 mm,在y方向上的测量误差为1.378~2.789 mm。
使用与分析弹丸1相同的方法分析弹丸2,对弹丸2着弹坐标E2进行误差分析与仿真,得到的仿真结果与弹丸1着弹坐标E1的仿真结果相同,即弹丸2着弹点E2坐标:在x方向上的测量误差为2.101~3.107 mm,在y方向上的测量误差为1.378~2.789 mm。
3 静态模拟实验
由于单管超高速射武器两发弹丸同时过幕的概率极低[14],因此,无法采用实弹射击的动态试验检验系统性能,但可以采用静态实验模拟两发弹丸同时着靶来检验系统性能。静态模拟实验的装置如下:一套三角阵列光电探测系统、两个直径为5.8 mm,长度为70 mm的圆柱形磁铁棒和一个贴有坐标纸的钢板。将贴有分辨率为1 mm×1 mm的坐标纸的钢板放置在三角阵列光电探测系统的测量幕面后方,使得钢板与测量幕面平行且均垂直于地面。钢板与测量幕面的间距为50 mm;将圆柱形磁铁棒作为模拟弹丸;将两个模拟弹丸穿过测量幕面吸附在与系统有效测量靶面相对应的钢板平面范围内的任意位置,并使得磁铁棒与测量幕面垂直。由系统测量得到一组模拟弹丸的坐标数据,记为(xE1,yE1)与(xE2,yE2),视为弹丸穿过幕面的测量值;由钢板上的坐标纸可以直接读得一组模拟弹丸的坐标数据,记为(xE1′,yE1′)与(xE2′,yE2′),视为弹丸穿过幕面的真值;那么弹丸的坐标测量误差可以表示为
(14)
重复测量100组数据(如表1所示),表中的数据有一位估读位,对实验数据进行处理可以得到:系统测量得到的两组坐标:x坐标测量误差的绝对值最大为3.5 mm,y坐标测量误差的绝对值最大为3.2 mm;x坐标测量误差的平均值为1.75 mm,y坐标测量误差的平均值为1.54 mm。
系统双弹丸的识别范围用Z表示,x坐标测量误差的最大值用Xm表示,y坐标测量误差的最大值用Ym表示,则由
(15)
可以得到Z=4.74 mm。当双弹丸同时着靶的两弹丸间距大于4.74 mm时,该测量系统就可以将双弹丸区分开,既该系统的双弹丸识别范围不小于4.74 mm。实验数据见表1。
4 结论
提出了一种采用半导体光电探测阵列配合一字线激光器构建三角阵列的双弹丸坐标光电测量方法,建立了该测试系统的数学模型,推导了双弹丸着靶坐标测量解析式,由误差理论分析结果得到:三角形阵列光电探测系统识别双弹丸时,在x方向上的测量误差为2.101~3.107 mm,在y方向上的测量误差为1.378~2.789 mm。静态模拟实验结果表明:该系统识别双弹丸时,在x方向上的测量误差为0.1~3.5 mm,在y方向上的测量误差为0~3.2 mm,该方法可以实现间隔不小于4.74 mm双发弹丸同时着靶的坐标测量,满足超高速射身管武器系统的测试要求,且结构简单、成本低、校准方便、易于实现工程化,但该方法针对弹丸散布较大的身管武器射击密集度测试时,扩大后的探测靶面会出现探测灵敏分布不均,导致部分探测区域的目标捕获率降低。
表1 静态模拟实验数据

组号每组编号纸靶xE′/mm测量靶xE/mm纸靶yE′/mm测量靶yE/mm误差ΔxE/mm误差ΔyE/mm0112 079.52 076.31 890.01 892.73.2-2.722 565.02 562.71 882.51 882.52.300212 308.02 307.21 268.51 271.30.8-2.822 175.02 171.51 723.51 721.43.52.10312 375.02 375.11 649.01 649.4-0.1-0.422 525.52 524.21 532.51 531.91.30.60412 406.02 404.81 311.51 312.51.2-1.022 963.02 962.91 912.51 910.60.11.9…1………………2………………9712 909.02 907.61 330.01 331.31.4-1.322 461.02 459.51 212.01 211.81.50.29812 304.02 303.11 168.51 168.20.90.322 712.52 711.11 226.51 229.71.4-3.29912 111.52 108.71146.01 144.82.81.222772.52 771.71 133.01 133.40.8-0.410012 353.52 351.81 046.01 043.91.72.122 634.02 632.91 070.51 070.71.1-0.2最大值3.5-3.2最小值0.10
注:小数点位为估读位

