以成功概率最大为目标的装备维修策略研究

肖 雨，韩小孩，孙晋聪，张剑波

(中国人民解放军66325部队，北京 102205)

传统的装备维修策略，无论是事后维修、定时维修还是基于状态的维修，都是从保障装备战备完好性的角度出发，安排维修工作，以减少故障和故障的损失。然而，装备任务开始时质量完好，并不一定能保证任务期间不发生故障，不一定能保证任务完成。因此，有必要从保障任务完成的角度出发，研究装备基于任务的维修决策。目前，基于任务的维修决策方面的研究已取得一些成果。文献[1]研究了不完全可修系统的任务成功性评估方法；如文献[2]以总体维修费用为约束研究了串并联加工系统的选择性维修方法；文献[3]中以维修保障资源为约束，以任务可靠度最大为目标，研究了考虑拼修活动在内的多种维修活动的维修任务选择方法；文献[4]中研究了维修保障资源、任务前维修时间双重约束下，以任务可靠度最大为目标的维修任务选择方法；文献[5]中研究了不完全维修条件下的冷贮备可修系统任务前维修方案优选方法；文献[6]中研究了不完全维修方式下的多状态系统维修任务选择方法；文献[7]中以任务可靠性为最大为目标研究了部件寿命服从Weibull分布的装备维修策略优选方法；文献[8]中研究了维修保障资源约束下，以任务可靠度最大为目标的舰船装备选择性维修策略；文献[9]中在给定时间约束下，研究了以任务可靠度最大为目标的任务前修复性维修工作选择方法。尽管这些研究都是以任务为依托进行维修决策，但是只能从任务可靠度的角度出发制定装备任务前维修方案，并未考虑任务中维修对任务成功概率的影响。尽管文献[10]中考虑了任务中维修队任务成功概率的影响，但是仅仅考虑单个部件，未从装备系统角度进行决策分析。

任务可靠度可认为是装备在特定任务剖面内完成规定功能的能力(任务可靠性)的一种度量。它可认为是装备在任务期间故障规律的一种体现。任务成功概率主要指装备在任务开始时处于可用状态的情况下，在规定的任务剖面中的任一(随机)时刻，能够使用且能完成规定功能的概率。

对于任务中不可维修的装备，其任务成功概率等于任务可靠度。现有研究多基于该情形展开。对于任务中允许维修的装备，其任务成功概率可认为是任务可靠性与任务维修性的综合体现，任务中的维修工作是影响任务成功概率的重要因素。此外，由于任务中的维修工作需要消耗一定的备件且需花费相应的费用，这必将影响装备任务前预防性维修时的可用费用及备件数量，从而影响任务前预防性维修的有效实施。现有研究并未对这些问题进行探讨。

本研究主要针对任务中可修装备，综合考虑任务前以及任务中的维修工作与任务成功概率之间的关系，研究以任务成功概率最大为目标的装备维修决策方法。在任务前维修时间、任务总体费用以及备件数量三方面约束下，以任务成功概率最大为目标，制定最佳的任务前预防性维修方案。

1 装备任务成功概率计算方法

在计算任务成功概率时要充分考虑装备的任务可靠性和任务维修性。任务可靠性通常用任务可靠度表示，任务维修性则用任务维修度表示。计算时，可将装备分为任务期间不可修部分和可修部分分别进行研究。对于不可修部分只需分析其任务可靠度；对于可修部分则需综合分析任务可靠度与任务维修度。

装备任务成功概率仅与任务功能单元相关，与非任务功能单元无关。因此，在计算任务成功概率时仅需分析任务功能单元的影响即可。同理，以任务成功概率最大为目标进行维修决策时，仅考虑任务功能单元的维修工作。

在任务过程中，若某几个单元同时发生故障时方可影响任务(任务成功或失败)，则认为这几个单元之间在功能上存在“并联关系”。将存在“并联关系”的多个单元视作一个整体，为保障任务的时效性，在任务过程中该整体发生故障(极端情况为各单元均故障)后仅对维修时间消耗最小的单元进行维修。由于篇幅有限，本研究不对“并联关系”进行过多讨论。将存在“并联关系”的单元视作整体后，装备可认为是一个纯串联系统。

假设某任务中装备共有n个可影响任务的功能单元(存在并联关系的多个单元视作一个整体，为一个功能单元)记作a1,a2,…,an。其中前r个功能单元为任务中不可修单元，其余为可修单元。任务中允许的最大维修时间为T。令各功能单元的任务可靠度为R1,R2,…,Rn，可修单元维修时间概率密度函数为mr+1(t),mr+2(t),…,mn(t)。则不可修部分任务成功概率PN为

(1)

可修部分任务可靠度为

(2)

将可修部分整体记作E，可知E发生故障的概率等于ar+1,ar+2,…,an中至少有一个发生故障的概率。令n-r个可修单元的每一种故障组合(各组合事件之间互斥)为E的一个故障事件，则E共有2n-r-1个可能的故障事件，其中第i个故障事件记作Ei。例如，假设故障事件Ei为：第r+j个与第r+k个功能单元发生故障，其余可修单元不发生故障。则Ei发生的概率为

故障事件Ei发生后在T内被排除的概率为：M(Ei)=P(Tr+j+Tr+k≤T)。其中Tr+j，Tr+k分别代表第r+j个与第r+k个功能单元发生故障后维修所需时间。

根据卷积计算公式可知

(3)

可计算可修部分E的任务维修度为

(4)

进而计算可修部分任务成功概率PY为

PY=RM+(1-RM)M(E)

(5)

最终得装备任务成功概率PS为

PS=PN×PY

(6)

2 以成功概率最大为目标的装备维修决策模型

根据任务确定决策目标是基于任务的维修决策的基本前提。通常情况下，如果装备需完成重要任务或者任务失败后果较为严重，应以任务成功概率最大为目标进行决策。而对于一般任务，在任务成功概率满足要求的前提下，可适当考虑以任务总体费用最小为目标进行决策。两种决策目标下的维修决策的本质是一致的。都是根据决策约束条件，制定满足决策目标的最佳维修方案。因此本文仅研究以任务成功概率最大为目标的维修决策方法。

考虑到装备任务的时效性要求，参与任务的各功能单元在任务中发生故障后，通常选择维修时间最短的维修方式进行维修，可根据各功能单元采用不同维修方式时的维修时间长短进行决策，此处不加赘述。

在给定任务前预防性维修时间、任务总体费用、备件数量三方面约束条件下，以任务成功概率最大为目标的维修决策基本过程如图1所示。

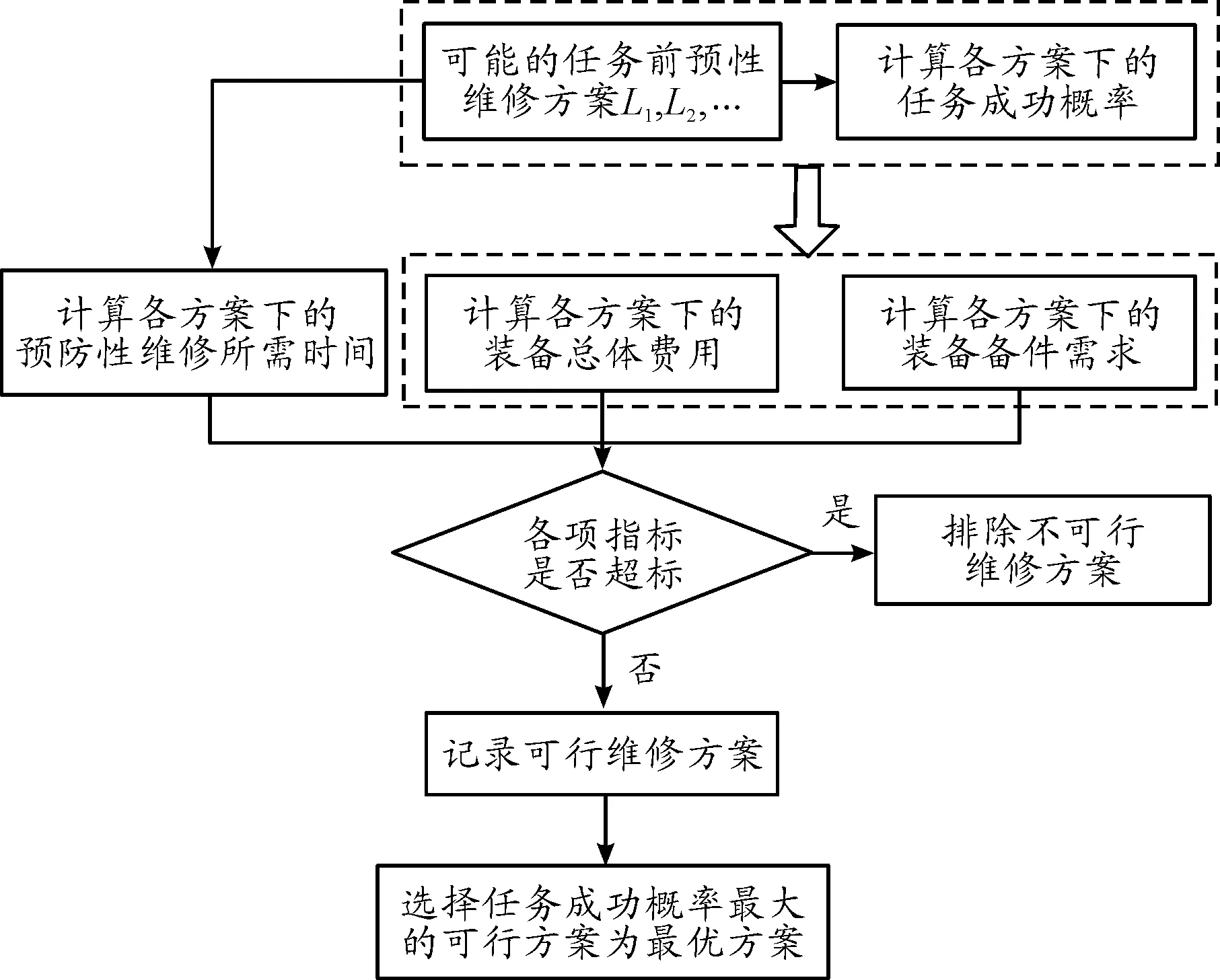
图1 以成功概率最大为目标的维修决策基本过程框图

图1中，可能的任务前预防性维修方案是指各任务功能单元依据各自技况，在任务前采取的预防性维修工作的一个有机组合。决策的核心内容为：计算各种维修方案下装备任务成功概率；计算装备任务前预防性维修时间，任务总体费用以及备件需求。其中，任务成功概率计算问题上文已详细讨论，在此不加赘述。下面主要讨论装备预防性维修时间、任务总体费用以及备件需求三方面内容的计算方法。

1)装备任务前预防性维修时间计算方法

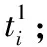
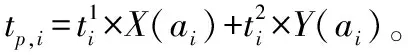
(7)

考虑到功能单元的维修时间通常为服从某一分布的随机变量，Tp可理解为服从特定分布的随机变量，其分布规律可通过相关功能单元维修时间概率密度函数的卷积计算获取。

2)装备任务总体费用计算方法

装备任务总体费用包括装备的使用费用、任务失败时的损失以及装备的任务总体维修费用三部分。其中，装备的使用费用和任务失败时的损失通常不受上述维修工作的影响，可根据实际任务要求确定，分别记作CU、CS；任务总体维修费用记作CM。则装备的任务总体费用为

C=CM+(1-PS)CS+CU

(8)

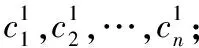
(9)

令各任务中可修单元在任务中进行维修时的费用分别为cm(r+1),cm(r+1),…,cmn。当任务失败时，尽管装备可能在任务中进行了一些维修工作并产生了相应维修费用，但是由于考虑到装备的任务失败概率通常不会太大，且这些费用远小于装备损失，因此可忽略不计。当任务成功时，若装备任务中可修部分未发生故障，则不进行维修；若发生故障，则无论可修部分在任务中发生哪种故障事件都将被排除。因此，装备在任务中产生的维修费用为

(10)

可见，装备任务中的维修费用很大程度上取决于装备的任务成功概率和功能单元任务可靠度。二者与装备的任务前预防性维修工作存在密切关系。因此，装备任务中的维修费用在一定程度上受限于装备所采取的任务前预防性维修策略。

可知，装备的任务总体维修费用为

(11)

将上述计算结果代入式(8)可得装备的任务总体费用。

3)装备备件需求计算方法

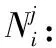
(12)

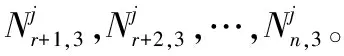
(13)

与式(1)中原理相同，装备任务中维修工作的备件需求同样受限于装备所采取的任务前预防性维修策略。

对Nj1、Nj2求和可知，装备所需消耗的第j类备件的总数为

(14)

为保证Nj为整数，对计算结果向上取整。同理，可求得装备对各类备件的需求为：N1,N2,…,Nm。

假设，执行某任务时装备任务前最大允许维修时间为Tmax，可承受的最大任务总体费用为C*。则基于任务的维修决策问题可转换为如下优化问题。

maxPS

(15)

s.t.P(Tp≤Tmax)≥γ

(16)

C≤C*

(17)

N1≤n1,N2≤n2,…,Nm≤nm

(18)

其中，γ是0到1之间的一个常数，可根据实际任务情形设定。

目标表达式(15)表示装备任务成功概率取最大值。

约束表达式(16)表示装备任务前预防性维修工作能在任务前允许维修时间内完成的概率不小于γ。

约束表达式(17)表示装备任务总体费用不超过可承受的最大任务总体费用C*。

约束表达式(18)表示在相应维修方案下，装备对各类备件的需求均不超过各类备件的可用量。

3 以任务成功概率最大为目标的维修决策模型求解

分析上述维修决策模型可知，决策问题的实质是多个参数的组合优化问题，可用现代优化算法求解。考虑到各功能单元维修策略的离散性特点，本文主要借鉴离散粒子群优化算法对维修方案进行寻优。离散粒子群优化算法简单、易行，便于依据决策模型构建优化模型。

由于篇幅有限，此处仅对最佳维修方案的计算步骤进行说明，至于计算中用到的粒子群构建及求解过程请参阅文献[11]。

结合本文研究内容，依据粒子更新基本规则，现给出如下计算步骤：

步骤1：初始群参数设定。① 对任务剖面进行分析，确定任务前最大允许维修时间Tmax以及参数γ的数值；② 确定可用的备件数目n1,n2,…,nm；③ 根据规则构建粒子群，确定粒子群的数量参数、惯性权重、加速常数以及最大更新次数。

步骤2：随机选取一定数量可能的维修方案，构造初始粒子群，并在此基础上设定各粒子初始更新速度。

步骤3：根据式(16)～式(18)约束条件，判断各粒子所对应维修方案是否可行。若可行，则利用式(6)计算任务成功概率，当作该粒子的适应度；若不可行，则适应度为0。根据各粒子适应度数值，计算粒子群中各粒子的当前最佳位置以及群最佳位置。

步骤4：根据文献[11]中更新规则对粒子群进行一次更新，此后重复步骤3，更新各粒子当前最佳位置和群最佳位置，并对粒子群更新速度进行一次更新。

步骤5：重复步骤4直到更新次数达到最大更新次数为止。提取此时的群最佳位置，得最优的维修方案。

4 示例分析

已知某任务，要求某装备持续工作状态时间为10 h；任务中最大允许维修时间T=3 h；任务前最大允许维修时间为Tmax=5 h，γ=0.85；装备可承受的任务总体费用为4万；与任务相关的备件共有5类(D1、D2、D3、D4、D5)，可用数量均为4。现以任务成功概率最大为目标对装备实施维修决策，选择最佳的预防性维修方案。

分析装备结构以及任务特点可知，参与执行任务的功能单元共有7个，分别为：a1,a2,…,a7。其中a1～a4在任务中不可修，a5～a7在任务中可修。在日常维修工作中，a1、a2、a7采用“修复如旧”策略；a3～a5采用“修复如新”策略；a6采用“不完全维修”策略。根据文中方法，可分别计算各功能单元实施各类任务前预防性维修工作后的任务可靠度，并记录预防性维修费用(万元)以及维修时间分布(min)如表1所示。各功能单元实施相应维修工作时，对备件的需求如表2所示。

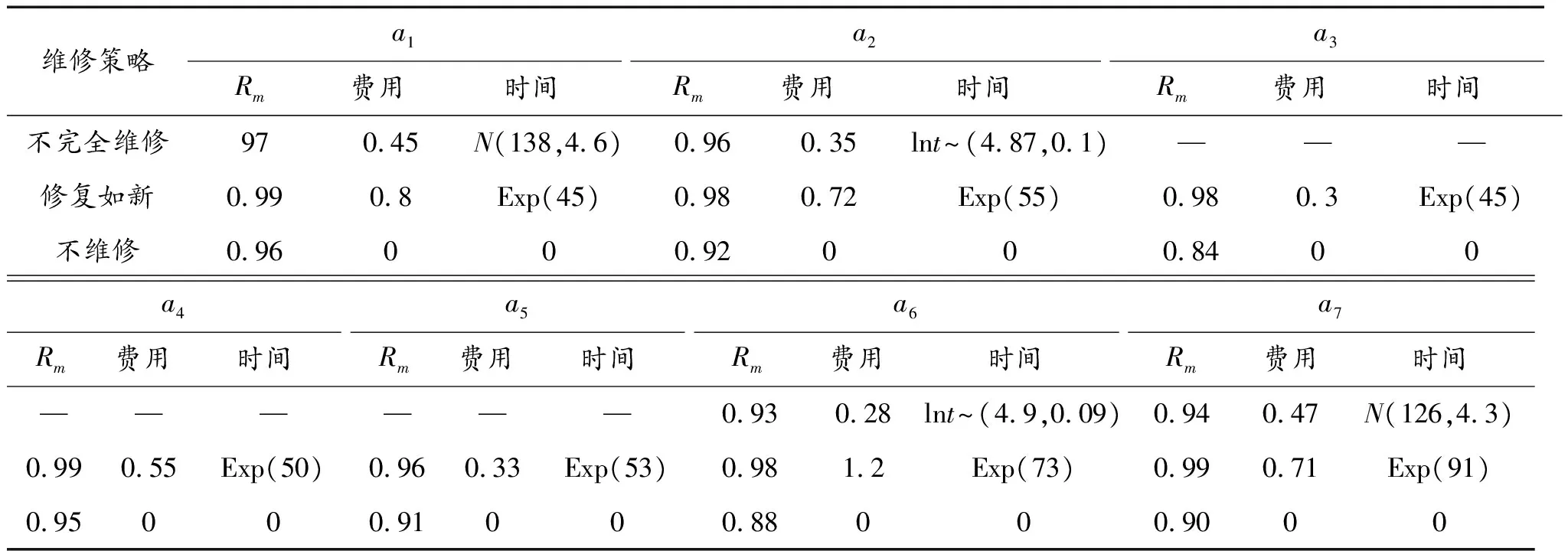
表1 任务前预防性维修后功能单元任务可靠度及维修费用与维修时间

表2 功能单元维修保障资源需求量

功能单元a5～a7在任务中的维修费用分别为：0.33万、0.2万、0.3万；任务失败造成的损失为：10万；装备的使用费用为0.4万。

根据历史维修数据统计分析可知，a5的维修时间(min)服从均值为30.9，方差为5.5的正态分布；a6的维修时间(min)服从均值为45的指数分布；a7的维修时间服从对数均值为4.8，对数方差为0.1的对数正态分布。可计算3个单元维修时间概率密度函数m5(t)、m6(t)、m7(t)。

将a5、a6、a7看作一个整体E。可知，E共有7类故障事件，分别为：E1(a5发生故障，a6、a7不发生故障)、E2(a6发生故障，a5、a7不发生故障)、E3(a7发生故障，a5、a6不发生故障)、E4(a5、a6发生故障，a7不发生故障)、E5(a5、a7发生故障，a6不发生故障)、E6(a6、a7发生故障，a5不发生故障)和E7(a5、a6、a7均发生故障)。根据维修时间概率密度函数m5(t)、m6(t)、m7(t)，利用式(3)可计算在规定时间T内各事件被排除的概率为：M(E1)≈1；M(E2)≈0.981 7；M(E3)≈1；M(E4)≈0.963 1；M(E5)≈0.967 1；M(E6)≈0.715 3；M(E7)≈0.431 9。

1)维修决策需求分析

当不进行任务前预防性维修时，利用第1节中方法，可计算各故障事件的发生概率为：P(E1)=0.071 3；P(E2)=0.098 3；P(E3)=0.080 1；P(E4)=0.009 7；P(E5)=0.007 9；P(E6)=0.010 9；P(E7)=0.001 1。进而利用式(4)～式(6)计算得装备的任务成功概率PS=0.700 5。在此基础上，利用式(8)计算装备的任务总体费用为3.42万。由于该维修方案下装备的任务成功概率过小，应进行任务前预防性维修。

当进行最大预防性维修，即所有功能单元均“修复如新”时，经计算可知任务前不可能在允许时间内完成维修工作。因此，该维修方案不可取，需重新制定维修方案。

2)根据决策目标制定最优维修方案

利用文献[11]中方法构建粒子群。将每个维修方案当作每个粒子，利用离散粒子群优化算法进行寻优。令ω=0.5，加速常数c1=c2=1.494 45，最大更新次数W=100，数量参数q=10。计算可得维修方案寻优过程如图2所示。

最终得最佳的维修方案为：a1、a5、a6、a7不进行维修；a2“不完全维修”；a3、a4“修复如新”。该方案下的装备任务总体费用为2.788 4万，P(Tp≤Tmax)=0.867 3>0.85，对各类备件的需求分别为(3,2,4,3,3)，均满足约束条件要求。此时，装备的任务成功概率为PS=0.888 6。

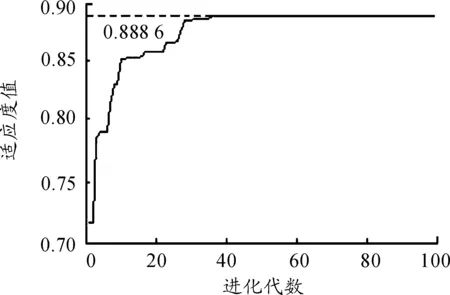
图2 维修方案寻优过程曲线

3)案例对比分析

以该案例相关约束条件为基础，利用传统方法从装备任务可靠度角度出发对装备进行维修决策，进而对比分析文中方法与传统方法之间的差异。

将上述例子中，以任务成功概率最大为目标的维修决策模型中的目标函数换为装备的任务可靠度，利用离散粒子群优化算法优化得最优维修方案为：a1、a5、a6、a7不进行任务前预防性维修；a2～a4以“修复如新”策略进行任务前预防性维修。该方案下，若不考虑任务中维修时，各类备件的需求分别为(3,1,4,2,3)。此时，a5、a6仍为任务中可修功能单元；结合表2中数据可知，a7在任务中维修需用到第3类备件D3，而在该维修方案下D3在任务中的可用量为0，因此a7在任务中不能进行维修。从而，计算装备任务总体费用为3.775万，P(Tp≤Tmax)=0.938 2>0.85，对各类备件的需求分别为(3,2,4,3,4)，均满足约束条件要求。装备的任务成功概率为PS=0.815 9。该方法计算结果与本文方法计算结果如表3所示。

表3 不同决策方法计算结果

由表3对比分析可知，采用本文决策方法所得维修方案，不仅任务总体费用、备件需求量均少于传统维修决策所得维修方案，而且可以达到更高的任务成功概率。较之传统方法，本文方法可得到更佳的维修方案。

5 结论

给定任务前维修时间、任务总体费用以及备件数量三方面约束，以任务成功概率最大为目标制定了最佳的任务前预防性维修方案。充分考虑了任务前及任务中维修工作对装备任务成功概率的影响，在实践任务中验证效果很好，为真实任务环境下的维修决策提供了思路。